砂卵石填料加筋土挡墙筋土荷载传递规律研究
2016-08-09王多银汪承志
王多银,高 超,汪承志,韩 超,仝 亚
砂卵石填料加筋土挡墙筋土荷载传递规律研究
王多银,高超,汪承志,韩超,仝亚
(重庆交通大学河海学院,重庆400074)
为了研究砂卵石填料加筋土挡墙筋土间荷载传递规律,将加筋土视作以土体为基体,筋带为增强的复合材料,在轴向受力情况下,将拉筋周围土体分为界面层和加筋有效影响层。基于加筋有效影响层内由筋带产生的附加剪应力沿法向呈线性衰减的假设,修正了传统剪力滞后模型,建立起加筋带平衡微分方程,解得加筋土挡墙筋带轴向应力分布规律解析解。通过与拉拔试验数据对比,发现理论推导与试验结果比较吻合。研究结果表明:砂卵石填料加筋土挡墙拉筋应力沿长度l方向呈先增大后减小的类抛物线形状,且峰值出现在<l/2处;紧邻拉筋部分土体出现带状加筋有效影响层,且附加剪应力在该土层内沿法向线性衰减。
砂卵石;加筋土挡墙;有效影响层;剪滞理论;荷载传递规律
doi:10.11988/ckyyb.20150332
1 研究进展
砂卵石主要分布于我国西南地区,其因压实性能好、透水性强,抗剪强度高等优良特性被广泛应用于高土石坝、路基、桥梁礅台、挡土墙等工程领域。近年来,随着加筋技术的成熟,以砂卵石为填料的加筋结构更是越来越受到工程人员的青睐。加筋土的工作原理为土体和筋材通过界面摩擦形成复合体,加强原土体的抗剪强度[1],其结构性能主要取决于筋土间的相互作用。
目前,国内外对于筋土相互作用研究已取得了丰富的研究成果。如丁金华、包承纲[2]利用弹性理论解得筋材连续分布情况下加筋土应力分布理论解,提出“加筋有效影响范围”的概念,并认为在该范围内剪应力呈线性衰减;周健等[3]应用离散元软件PFC2D模拟了格栅的拉拔试验,从模拟结果可以清晰地看到格栅上下一定区域内的土体在拉力作用下应力水平显著增大,验证了“加筋有效影响范围”的存在;杨广庆等[4],王祥等[5]对加筋土挡墙拉筋轴向应力、应变大小及规律进行了现场测试,发现拉筋应力沿长度l方向呈非线性分布规律,且峰值出现在<l/2处。但对于剪应力在填土中沿法向的传递规律尚无定论,且对砂卵石的研究主要集中于砂卵石的抗剪强度、剪胀性、弹性模量等方面[6-8],对以砂卵石为填料的加筋结构的研究却很少有人涉及。
剪力滞后理论是由Cox[9]研究包埋在某一无穷大的基体材料中的单根短纤维的问题时首次提出,而后经Rosen,Fukuda,Dow等不断完善,已形成相对完整的体系,并能很好地反映纤维与基体荷载传递特点[10-11]。
本文通过剪力滞后理论结合模型试验分别从筋带(条带式加筋材料)轴向应力分布和填土内剪应力沿法向传递2个方面分析了砂卵石填料加筋土挡墙筋土相互作用规律。
2 加筋挡墙筋带轴向应力公式推导
2.1传统剪滞模型
传统剪滞模型是由 Cox[9]于1952年提出,见图1。
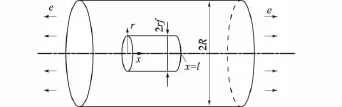
图1 传统剪滞分析模型Fig.1 Traditional shear-lag model
假设复合材料基体和纤维均为理想的线弹性体。在轴向受载时,由于基体和纤维之间的弹性差异使界面层上下发生相对位移,从而产生剪切应力。此剪切应力即为基体与纤维间应力的传递方式。该模型中纤维被视作圆柱体,并假设纤维只承受轴向拉力,而基体仅承受剪切荷载作用。但该模型未考虑纤维应力的有效传递范围,认为纤维应力将通过相对剪切发散到整个基体之中,这显然是有悖于圣维南原理的,因此有必要对剪力滞模型进行一定的修正再运用于加筋土的应力传递计算之中。
2.2剪滞模型修正与筋带应力公式推导
根据丁金华、包承纲的理论[2]及试验结果[12],将加筋土体分为3部分,即:筋土界面层、有效影响层和远离层对传统的剪滞模型予以修正。修正的剪滞模型如图2所示,筋带宽tf,厚hf,紧邻筋带表面的土体为筋土界面层,厚度可忽略不计。界面层之外厚为hd的土层即为加筋有效影响层。

图2 加筋土剪滞分析模型Fig.2 Shear-lag model of reinforced soil
尽管剪力滞后理论简单,但要求得全部解析解仍然比较困难。现根据杨广庆等[13]的研究成果,作如下进一步进行简化:①在小应力情况下,可将土体与筋带均视为线弹性体,即两者弹性模量均为常数;②筋土界面处土体与筋带结合完美,且仅受剪切应力作用;③有效影响层内剪切位移均平行于轴向,即剪切位移仅为y的函数。并且根据文献[2]假设:加筋有效影响层内由筋带产生的附加剪切应力沿法向呈线性衰减。
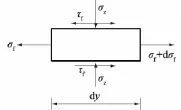
图3 微段受力分析Fig.3 Force analysisdiagram of micro-segment
现取筋带上长为dy的微段作受力分析(见图3)。由于筋带很薄,重力的影响很小,我们可认为筋带上下表面的法向应力相同。
假设筋带上下表面剪应力也相等,根据微段的受力平衡可得

式中:τf为筋土界面剪切应力(Pa);σf为筋轴向应力(Pa)。
整理上式得

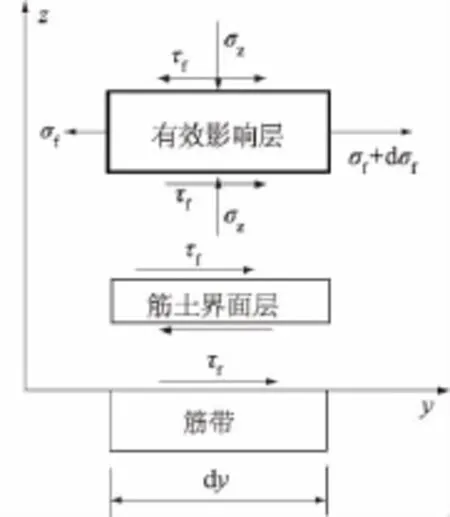
图4 剪滞模型应力拆分Fig.4 Stresses decouplingin shear-lag model
式(2)实为剪滞理论的基本公式。现在,推导的关键即为确定τf的表达式。筋带周围土体被分为筋土界面层和有效影响层,各层受力情况如图4所示。
筋土界面层很薄且层内土体只受剪切应力作用,加筋有效影响层水平方向受到正应力和剪切应力。其中τz为关于z的函数,根据假设,其数值沿z轴正向呈线性衰减。由此我们可以得到τz的表达式为


将式(3)代入式(4)得

对式(5)在0到hd之间关于z积分可得
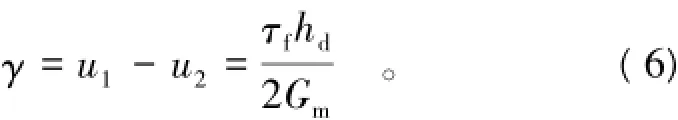
式中:γ为筋土界面层与有效影响层上边界轴向位移差;u1,u2分别为土体在hd和筋土界面处的轴向位移,由于筋土界面结合完美,则可认为u2为筋带的位移;Gm为土体的剪切模量(Pa)。对式(6)关于y微分可得

式中:Em为土体的弹性模量(Pa);Ef为筋带的弹性模量(Pa);σhd为土体在hd处的轴向正应力(Pa);σf为筋带所受轴向正应力(Pa)。由于在hd处,土体应力已经不受筋带影响,所以可取σhd为该处的土压强(若有竖向附加荷载可转换为等效土压强)。对式(2)两边关于y求导并代入式(7)有
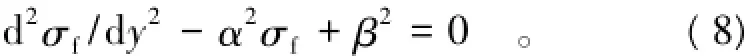
求解式(8)可得
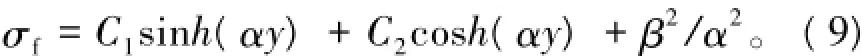
式中C1,C2均为常数。
边界条件为

式中T,A分别为筋带所受拉拔力和筋带截面面积。将式(10)代入式(9)得
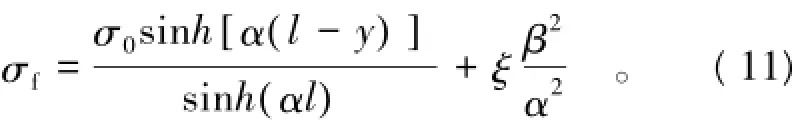
其中
式中l为筋带埋设长度。
2.3“加筋有效影响范围”的确定
从式(11)可以看出,加筋土挡墙拉筋沿轴向分布规律受到众多因素的影响,而其中确定“加筋有效影响范围”则是计算的关键。实际上,“加筋有效影响范围”也受到诸如界面摩擦系数、土体泊松比、筋带长度等众多因素的影响,本文引用丁金华、包承纲等[2]的研究成果加以确定。该文中,作者应用弹性理论分析了加筋前后的三轴实验土体,推导出对称条件下,加筋土体的竖向应力和剪应力增量。并且定义剪应力影响范围与筋带铺设长度之比为一无量纲参数δ,则本文中“加筋有效影响范围”取hd= δl。δ的表达式如式(13)所示。
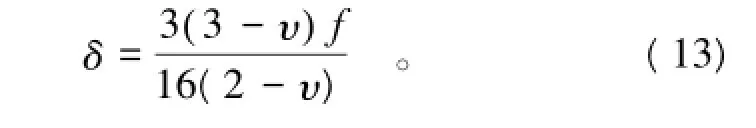
式中:υ为土体的泊松比;f为界面摩擦系数,f的取值按照水利水电工程土工合成材料应用技术规范(SL/T225—98)的规定。
3 可行性验证
本文关于加筋土挡墙筋带轴向应力的分布公式的推导是建立在加筋有效影响层内由筋带产生的附加剪切应力沿法向呈线性衰减的基础之上的,为了验证公式的可行性,本文特依托重庆交通大学国家内河航道中心港工实验室做了一组加筋土挡墙模型试验。
3.1模型尺寸及模型材料
如图5所示,试验在1.35 m×1.5 m×1.5 m(长× 宽×高)的高光亮有机玻璃槽中进行,通过机械千斤顶加反力系统施加拉拔荷载,拉拔力由压力传感器测得,筋带应变通过电阻应变片测得,应变片布置位置分别距离挡墙0.2,0.4,0.6,0.85,1.05,1.25 m。试验未施加竖向堆载。
加筋材料采用重庆永固建筑科技发展有限公司生产的钢塑带(CAT30015B),材料属性见表1。土样选择重庆地区常见的长江沿岸砂卵石填料,具体性质见表2。
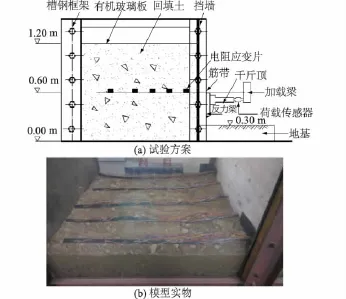
图5 试验装置示意图Fig.5 Sketch of test device

表1 筋带参数Table 1 Parameters of reinforced belt
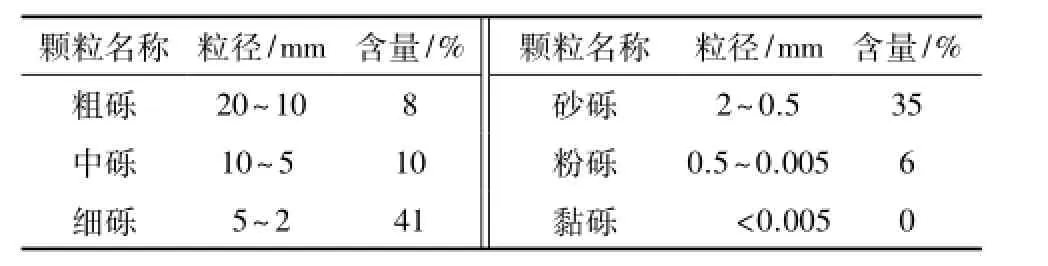
表2 土体颗粒组成Table2 particle composition of soil

表3 土体物理力学性质Table 3 physical-mechanical properties of soil
3.2试验步骤
试验前先填筑右侧基础,然后安置挡墙。左侧填土采用分层填筑并夯实。施加荷载采取分段式加载,即每次加载300 N左右,待筋带应变数据稳定之后进行下一级加载。施加荷载过程中,荷载不能继续增长时停止加载。
3.3试验结果与分析
图6为居中筋带应变沿轴向分布规律测试结果,其余4根测试规律与之类似,这里不予以一一列出了。
从图6中我们可以看出筋带在轴向拉力作用下,其应变并非越靠近拉力施加处越大,而是呈先增大后减小的类抛物线形状,且应变峰值出现在距离受力点<1/2筋带长度处。这与杨广庆等[4],王祥等[5]对其他土体测试结果相似,筋带尾端出现二次波动可能是由于埋设不平整导致应力集中造成的。
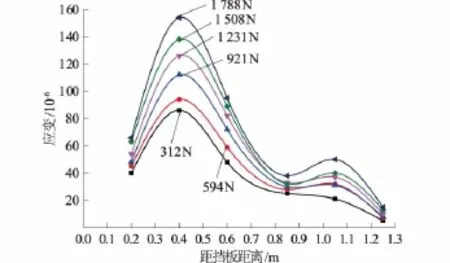
图6 筋带轴向应变分布Fig.6 Axial strain distribution of reinforced belt
在拉力为312 N时,将各参数代入式(11),得到筋带各点轴向应力值。然后根据在小应力下,筋带弹性模量为常数的简化,将上述应力值转换为应变值与模型试验实测值对比如图7所示。
从图7中可以看出,理论计算值分布于实测值两侧,理论计算值比较接近实测值,0.4 m与0.85 m处相差较大可能也是由于筋带埋设不平整造成的。因此,筋材产生的附加剪应力在加筋有效影响层内沿法向呈线性衰减的假设成立。
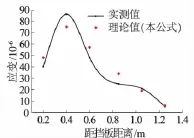
图7 试验数据和本文公式对比Fig.7 Comparison between experimental data and calculated results
4讨论
由于在式(11)推导过程中未限定土体类型,为了验证其对其他类型土体的应用可行性,以上述模型试验为原型,利用有限元软件ABAQUS分别对填土为黏土和砂土时筋带轴向应力分布进行计算。
有限元计算采用平面应变问题求解,挡墙和土体采用实体单元(CPE4R),筋带采用一维线性杆单元[14](T2D2),屈服准则采用 Mohr-Coulomb屈服准则。
4.1有限元网格划分
有限元网格划分如图8所示,总节点数1 184个,总单元数1 053个。
4.2计算参数选取
计算分别以黏土、砂土为填料进行有限元模拟,土体参数及模型材料参数见表4,拉拔荷载取1 000 N。
图8 有限元网格剖分Fig.8 Division of finite element meshes
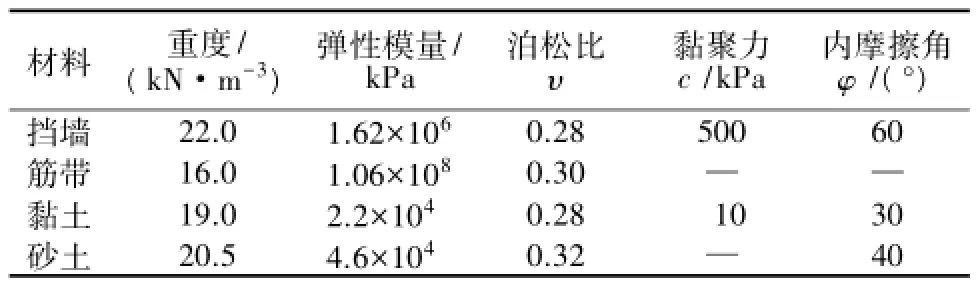
表4 加筋土挡墙的材料参数Table 4 Material parameters of reinforced soil retaining wall
4.3有限元计算结果分析
图9为黏土和砂土作为填料时筋带轴向应力有限元计算结果与理论公式推导结果之对比。

图9 有限元计算结果与本文公式计算结果对比Fig.9 Comparison between finite element resultsand theoretical calculated results
从图9中可以看出,填料为砂土时,理论计算结果与有限元计算结果比较吻合。而填料为黏土时,理论计算值远远大于有限元计算值,这可能是由于在公式推导过程中未考虑土体黏聚力造成的。因此,式(11)适用于加筋土挡墙填土为非黏性土体时条带式加筋材料在轴向受力情况下应力分布规律计算。
5结论
本文采用理论推导结合模型试验分析了砂卵石填料加筋挡墙在筋带轴向受拉情况下筋土间荷载传递的规律,可以得到如下结论:
(1)式(11)可用于加筋土挡墙填土为非黏性土体时条带式加筋材料在轴向受力情况下应力分布规律分析。
(2)砂卵石填料加筋挡墙拉筋轴向应力分布规律同其他填料的一致,均呈先增大后减小的类抛物线形状,应力峰值出现在y≤l/2处,且峰值的大小及位置与筋带埋设深度、筋带弹性模量、加筋有效影响层宽度等有关。
(3)筋带受拉时,筋带拉力通过剪应力的方式扩散到周围一定范围的砂卵石中,而在该范围之外的土体则不受到任何影响,称该范围为加筋有效影响层,且由筋材产生的附加剪应力在加筋有效影响层中沿法向呈线性衰减。
[1]SOLDOSSER F,LONG N T.Recent Results in French Research on Reinforced Earth[J].Journal of the Construction Division,1974,100(3):223-237.
[2]丁金华,包承纲.加筋复合土体的力学机理分析[C]∥第八届土力学及岩土工程学术会议论文集.北京:万国学术出版社,1999:441-444.
[3]周健,孔祥利,鞠庆海,等.土工合成材料与土界面的细观研究[J].岩石力学与工程学报,2007,26(1):3196-3202.
[4]杨广庆,蔡英.多级台阶式加筋土挡土墙试验研
究[J].岩土工程学报,2000,22(2):254-257.
[5]王祥,徐林荣.双级土工格栅加筋土挡墙的测试分析[J].岩土工程学报,2003,25(2):220-224.
[6]李振,邢义川 .干密度和细粒含量对砂卵石及碎石抗剪强度的影响[J].岩土力学,2006,27(12):2255-2260.
[7]褚福永,朱俊高,殷建华.基于大三轴试验的粗粒土剪胀性研究[J].岩土力学,2013,34(8):2249-2254.
[8]胡敏,徐国元,胡盛斌.基于 Eshelby张量和 Mori-Tanaka等效方法的砂卵石土等效弹性模量研究[J].岩土力学,2013,34(5):1437-1442.
[9]COX H L.The Elasticity and Strength of Paper and Other Fiberous Materials[J].British Journal of Applied Physics,1952,3(3):72-75.
[10]杨庆生.复合材料细观结构力学与设计[M].北京:中国铁道出版社,2000.
[11]高庆,康国政.短纤维复合材料应力传递的修正剪滞理论[J].固体力学学报,2000,21(3):198-204.
[12]丁金华,包承纲,丁红顺,等.南水北调中线工程土工格栅——膨胀岩的拉拔试验研究[J].南水北调与水利科技,2008,6(1):52-56.
[13]杨广庆,周亦涛,石乔勇,等.加筋土挡墙拉筋轴向应力分布规律研究[J].岩土工程学报,2013,35(4):650-654.
[14]任非凡,徐超,许强,等.山区超高加筋土路基力学行为的有限元分析[J].长江科学院院报,2014,31(3):101-105.
(编辑:王慰)
Rules of Load Transfer between Soil and Reinforcement in Reinforced Earth Retaining Wall with Sandy Cobble
WANG Duo-yin,GAO Chao,WANG Cheng-zhi,HAN Chao,TONG Ya
(College of River and Ocean Engineering,Chongqing Jiaotong University,Chongqing400074,China)
In order to study the rules of load transfer between reinforcement and soil in reinforced earth retaining wall with sandy cobble,the reinforced soil was considered as composite materials in which soil and reinforced belt was regarded as matrix and reinforcing material,respectively.The soil around the reinforcement was separated into the interface layer and the effective influence layer under axial load.Based on the hypothesis that the additional shear stress produced by the reinforcement turned to linear attenuation in the effective influence layer,we modified the traditional shear-lag model and established the stress equilibrium differential equation for the reinforcement,from which attained the axial stress analytical solution of the reinforcement.After comparing with the drawing test data,we found that the theoretical derivation was in accordance with the test results.According to the research,the axial stress of reinforcement increases firstly,and then decreases along the reinforcement length l,which shows parabolic-shaped distribution;and a maximum value appeared at a distance less than l/2 from the wall.The soil close to the reinforcement appeared banded effective influence layer,and the additional shear stress caused by the reinforcement in the effective influence layer turned to attenuate linearly along the normal direction.
sandy cobble;reinforced earth retaining wall;effective influence layer;shear-lag theory;load transfer rules
TU41
A
1001-5485(2016)07-0105-05
2015-04-20;
2015-05-12
国家自然科学基金项目(51209242)
王多银(1965-),男,四川遂宁人,教授,博士生导师,长期从事港口码头水工建筑物科研及教学工作,(电话)023-62652716(电子信箱)wdy@cqjtu.edu.cn。
