高速列车激励下大跨连续梁拱桥振动响应分析

李广慧，　孙 川

(1.中铁十六局集团第四工程有限公司，北京 101400；2.石家庄市城市建设投资控股集团有限公司，河北 石家庄 050051)



高速列车激励下大跨连续梁拱桥振动响应分析

李广慧，孙 川

(1.中铁十六局集团第四工程有限公司，北京 101400；2.石家庄市城市建设投资控股集团有限公司，河北 石家庄 050051)

摘要：以某大跨连续梁拱桥为研究对象，利用有限元软件ANSYS建立了该桥的3D动力分析模型，高速列车以质量-弹簧-阻尼模拟为多体系统，对高速列车作用下大跨连续梁拱桥的车桥动力响应进行了仿真分析；在此基础上，探讨了不同列车参数对桥梁的动力响应影响。分析表明：在高速列车激励下，连续梁拱桥的最大动态响应均发生在列车行驶至各跨跨中附近时；列车速度对桥梁动力响应的影响较大，而列车弹簧刚度对桥梁动力响应的影响相对较小。

关键词：连续梁拱桥；列车激励；振动响应

高速列车通过时，因耦合振动所引起的冲击荷载和惯性荷载都较大，对桥梁的振动影响不容忽视，大跨桥梁的车激响应研究引起广泛关注。李慧乐等[1]建立三维车辆模型及桥梁有限元模型，依据轮轨接触关系形成车桥耦合动力系统模型；考虑轨道不平顺的随机激励作用，求解车桥系统动力方程，得到桥梁节点的振动响应。王慧东等[2]用模态坐标法研究了高速列车与大跨度道岔连续梁的空间耦合振动中的桥梁响应问题。张鹏等[3]将车辆简化为两自由度体系，研究了车辆荷载激励下的多跨连续梁桥的减振问题。冉志红等[4]以钢筋混凝土拱桥为研究对象，基于一些简化假设，通过工程实例的模拟计算，提出冲击效应的简化分析方法。

连续梁拱桥充分利用了梁和拱各自的受力特点和优势，优化了结构受力状态，节约了材料，在桥梁造型上也有所创新，是铁路和公路桥梁中值得研究和推广的一种桥式，在我国高速铁路大跨桥梁中得到了越来越多的采用。但目前针对这种新型桥梁结构车激响应的研究尚未有文献报道。有鉴于此，本文以某大跨连续梁拱桥为研究对象，基于ANSYS分析软件，建立车桥耦合的有限元分析模型，研究高速列车激励下的桥梁动力响应，并探讨列车车速、悬挂系统弹簧刚度等参数对桥梁动力响应的影响。

1 工程概况

某连续梁拱桥桥跨布置为(90+180+90)m，主梁为预应力混凝土结构，采用单箱双室变高度箱形截面。梁体全长361.6 m，中墩处梁高10 m，中跨跨中梁高4.5 m，边跨端部梁高4.8 m；箱梁顶板宽14.2 m，中支点处局部顶宽16.6 m；箱梁底板宽10.8 m，中支点处局部宽13.8 m；箱梁采用纵、横、竖三向预应力。拱肋计算跨度180 m，矢高36 m，矢跨比1/5；两片拱肋中心距为11.9 m，每肋由2∅1 100 mm钢管组成，每片拱肋两弦管中心距离2.0 m；横撑采用∅900 mm和∅1 000 mm的空钢管；弦管及缀板内填充C50微膨胀混凝土。桥跨布置如图1所示。

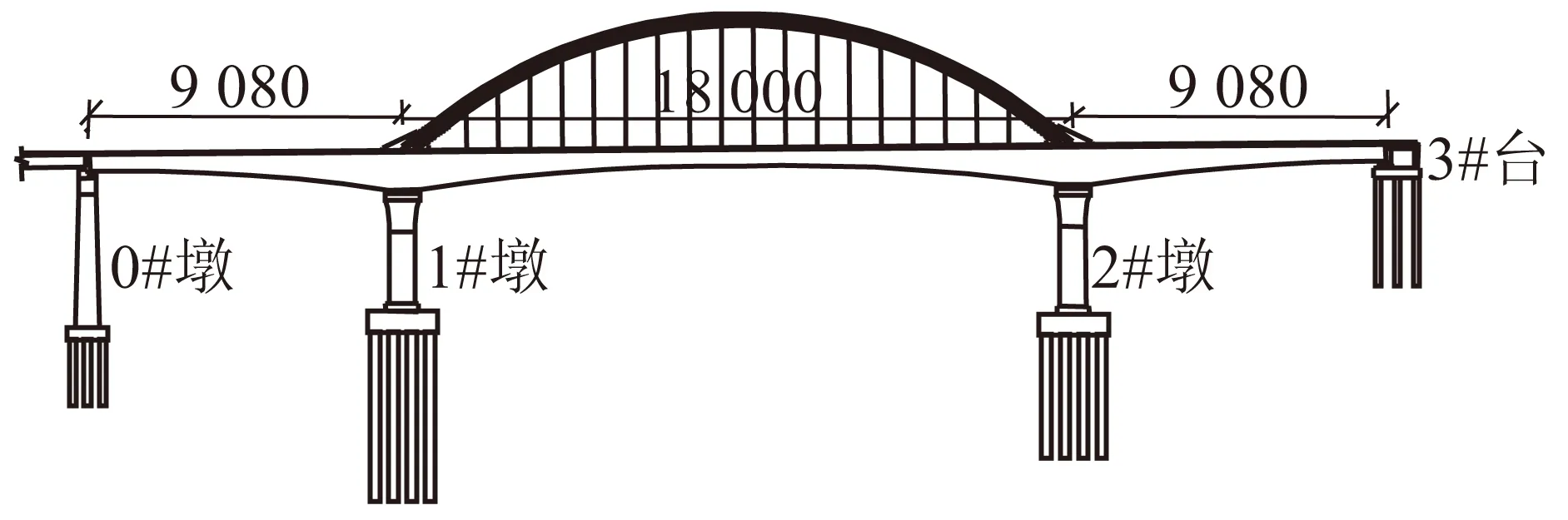
图1　桥跨布置图(单位：cm)

2 有限元模型

2.1 桥梁有限元模型

本文将桥梁以杆系结构进行离散，其中连续梁和拱肋均采用空间梁单元Beam189模拟，366根预应力钢筋采用空间杆单元Link8模拟，34根吊杆采用仅拉的link10单元模拟。主梁与吊杆的连接以及主梁与预应力钢筋的连接均采用无质量的刚臂连接，刚臂采用beam44单元，通过扩大其弹性模量来实现。ANSYS建立的三维空间有限元模型约5.8万个单元、3.2万个节点。约束情况为2#墩梁固结，其余为纵向自由活动。有限元模型如图2所示。

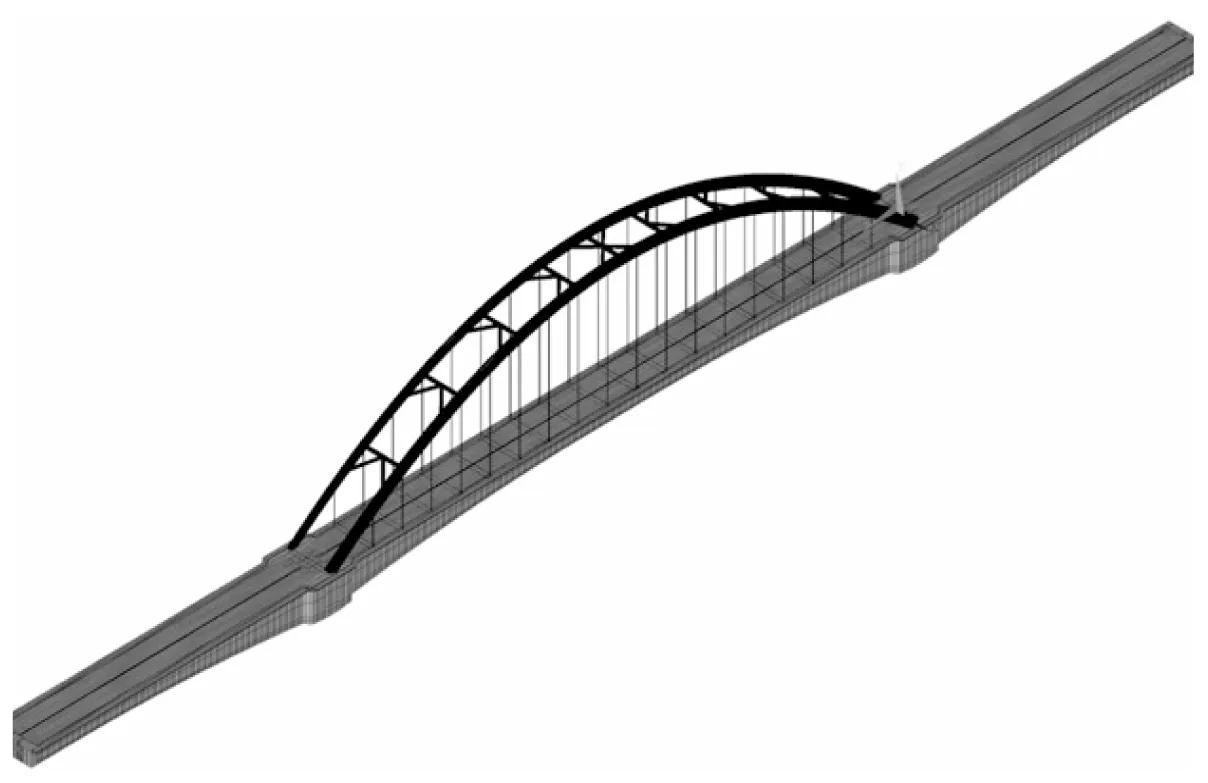
图2 有限元分析模型

2.2 车辆模型

车辆模型采用如图3所示的二系悬挂四轴高速列车模型，其中转向架与轮对为一系悬挂，转向架与车体为二系悬挂，采用线弹簧和粘性阻尼连接，悬挂系统参数如表1所示。为简化分析过程，作如下假定：

(1)仅考虑列车的竖向自由度，即车体沉浮与点头两个自由度。

(2)在行进过程中，列车轮对与桥梁始终保持紧密接触，且车体、转向架、轮对等各刚体均在平衡位置附近作小位移振动。

(3)列车的质量分布、悬挂参数等均对称。

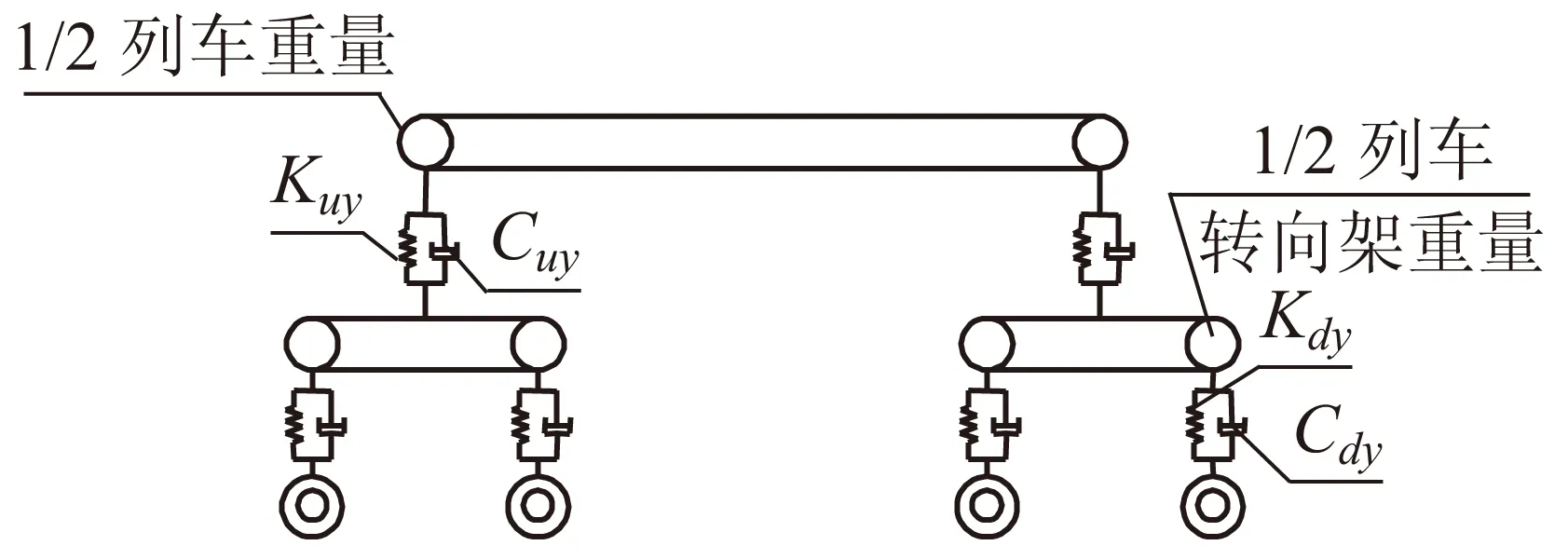
图3 列车分析模型

参数列车质量/t转向架质量/t 一系垂向悬挂 刚度Kdy/(kN·m-1)阻尼Cdy/(N·s/m) 二系垂向悬挂 刚度Kuy/(kN·m-1)阻尼Cuy/(N·s/m)数值38017272550162560

3 车激动力响应

利用生死单元技术，分析列车过桥过程，可得到连续梁拱桥的车激响应。限于篇幅，本文仅给出各跨跨中节点的位移响应、加速度响应以及弯矩响应曲线如图4～图6所示。

从图4可以看出，在列车通过全桥过程中，各跨跨中位移的最大值均发生在列车行驶至该位置时，当列车在其他跨行驶时，本跨跨中位移均有上扬波动趋势。由于结构对称，左跨跨中节点位移和右跨跨中节点位移变化规律相同，且位移幅值相同。同时可以看出：在列车荷载作用下，各跨跨中节点位移幅值较为接近，这说明本桥桥跨布置较为合理。

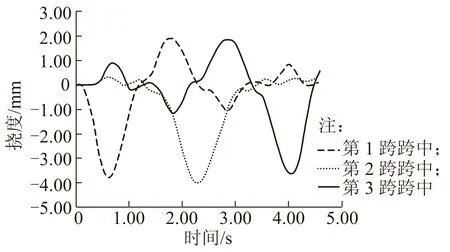
图4　连续梁拱桥各跨跨中竖向位移响应

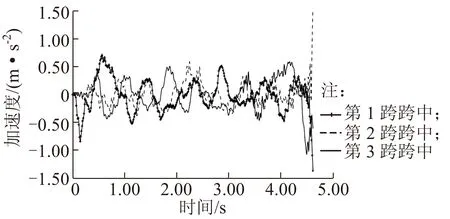
图5　连续梁拱桥各跨跨中竖向加速度响应

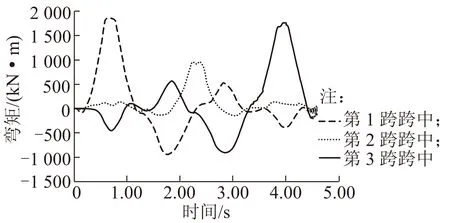
图6　连续梁拱桥各跨跨中弯矩响应

从图5可知：在列车荷载激励下，桥梁各跨跨中节点加速度基本按正弦规律变化，峰值基本相等。

从图6可知：列车过桥时，桥梁边跨跨中截面弯矩变化较主跨跨中截面弯矩变化剧烈，最不利荷载位置发生在边跨跨中。

综上所述，高速列车作用下，大跨连续梁拱桥竖向动位移最大值为4.046 cm，远小于我国《铁路桥涵设计基本规范》(TB 10002.1—99)规定的L/1000(18 cm)的容许值；加速度峰值均远小于我国《秦沈客运专线综合试验段线桥养护维修技术条件》(科技基函2002—103)规定桥梁垂向加速度限值0.35 g，这在一定程度上可以说明该大跨连续梁拱桥的动力性能良好。

4 车辆参数对桥梁动力响应的影响

4.1 车速影响

车速是影响桥梁动力响应的重要因素。为了分析不同车速的影响，取3种车速，进行列车通过桥梁时的动力响应分析。限于篇幅，仅给出了主跨跨中节点位移在不同车速时的变化情况如图7所示，各跨跨中节点在250 km/h、300 km/h、350 km/h三种车速下主要动力响应幅值如表2所示。

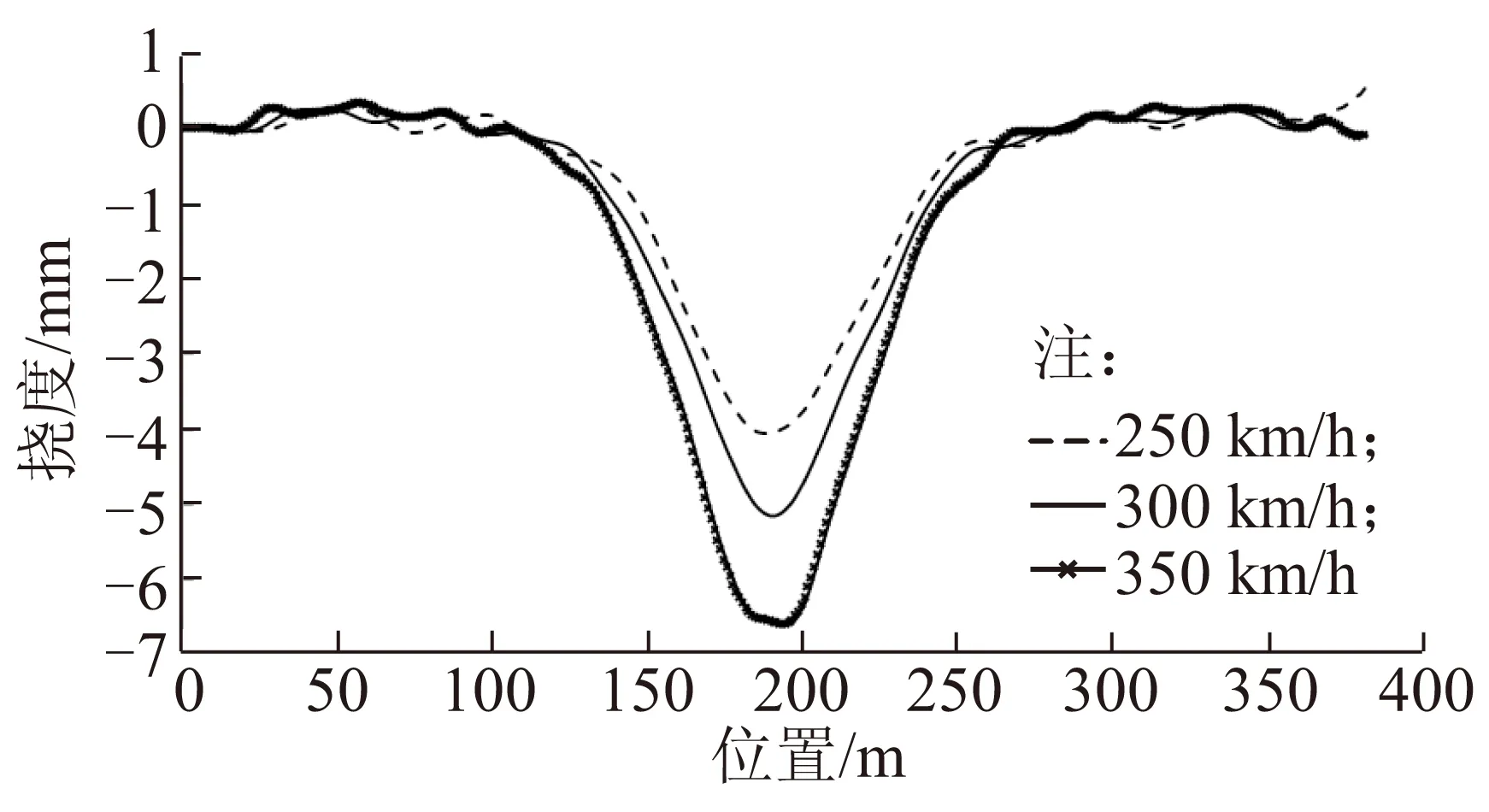
图7　不同车速下主跨跨中位移响应

车速/(km/h) 左边跨跨中 ①/mm②③④/(m·s-2) 中跨跨中 ①/mm②③④/(m·s-2) 右边跨跨中 ①/mm②③④/(m·s-2)2503.7261.4451.2490.5544.0411.2461.1620.5963.6241.4431.2450.5453004.3531.4681.4390.5725.1471.2441.3130.6094.2971.4671.4340.5803505.6191.5381.8380.6066.5791.2471.7360.6395.6221.5341.8840.618

注：①最大竖向位移；②弯矩冲击系数；③挠度冲击系数；④最大竖向加速度。

从图7可知，不同车速行驶过该桥时，桥梁中跨跨中节点动位移变化规律相同，最大动位移均发生在列车在该位置附近时，且随着车速增大，最大动位移呈增大趋势。

从不同车速下动力响应幅值可知：随着车速的提高，各跨跨中节点的动力响应均呈增大趋势，位移(挠度)冲击系数的变化明显强于内力(弯矩)冲击系数的变化，这说明车速对大跨度连续梁拱桥动位移的影响大于对结构动内力的影响。同时可以看出：在相同车速下，连续梁拱桥边跨跨中的挠度冲击系数略大于中跨跨中。

4.2 弹簧刚度影响

列车悬挂弹簧刚度对桥梁的动力响应有一定的影响。取0.5倍、1.0倍、1.5倍三种弹簧刚度系数，分析了列车通过时的桥梁动力响应。不同弹簧刚度时，桥梁中跨跨中竖向挠度曲线如图8所示，不同刚度系数下桥梁动力响应极值如表3所示。

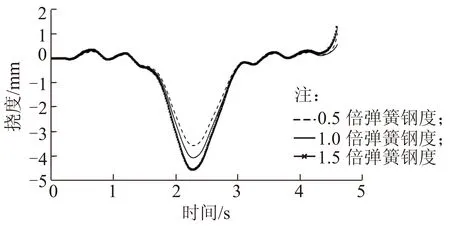
图8　连续梁拱桥各跨跨中弯矩响应

弹簧刚度 左边跨跨中 ①/mm②③④/(m·s-2) 中跨跨中 ①/mm②③④/(m·s-2) 右边跨跨中 ①/mm②③④/(m·s-2)0.5倍3.3211.4471.0850.6033.5451.2430.9350.5423.2211.4461.0800.5631.0倍3.7271.4461.2480.6554.0101.2431.1640.5963.6251.4441.2470.6461.5倍4.2211.5441.3790.7614.5381.2471.1980.6894.0431.5421.3490.701

注：①最大竖向位移；②弯矩冲击系数；③挠度冲击系数；④最大竖向加速度。

从图8可知，弹簧刚度对中跨跨中节点动位移的影响相同，不同弹簧刚度时，中跨跨中挠度出现最大值的时刻接近，且大致都是列车行驶至跨中附近；中跨跨中动位移随弹簧刚度的增加而增大；列车荷载行驶在边跨时，中跨跨中竖向挠度有稍许波动，波动规律基本一致。列车悬挂弹簧刚度大时，列车对桥梁的作用加大，导致振动增强。

从不同弹簧刚度各跨跨中节点动力响应幅值分析可知：随着弹簧刚度的增大，各跨跨中竖向动位移幅值和加速度峰值均呈增大趋势。竖向位移冲击系数受弹簧刚度影响较大，弯矩冲击系数对弹簧刚度不够敏感。总体上挠度和弯矩冲击系数随着弹簧刚度增大而增大。

5 结论

(1)相比于大跨度的连续梁桥，大跨度连续梁拱桥由于中跨拱肋和吊杆的作用，承载能力得以提高，在列车过桥时的动态响应同规范限制相比，相对较小，表明该类桥梁具有较好的动力性能。

(2)车速是影响大跨度连续梁拱桥动力响应的主要因素之一，桥梁控制截面动力响应极值和冲击系数等随车速的增加而增大。

(3)车辆弹簧刚度对大跨度连续梁拱桥动力响应有一定的影响，随着车辆弹簧刚度的增大，桥梁动力响应也呈增大趋势。

参考文献

[1]李慧乐,夏 禾,张 楠，等.基于车桥耦合动力分析的桥梁动应力计算方法[J].中国铁道科学，2015,36(1):68-74

[2]王慧东,马其森.韩江大桥(48+80+80+88+48)m道岔连续梁车桥耦合动力响应分析[J].石家庄铁道大学学报：自然科学版，2015,28(1):12-17

[3]张 鹏,钟晓林,李 星，等.车辆荷载激励下多跨连续梁桥的减振研究[J].广州建筑，2015,43(5):22-25

[4]冉志红,林 帆,陶蜀昆，等.车辆对钢筋混凝土拱桥的冲击效应简化分析方法研究[J].公路工程，2015,40(6):40-43

收稿日期：2016-04-27

作者简介：李广慧(1974—)，女，高级工程师，主要从事交通土建工程技术管理工作

DOI：10.13219/j.gjgyat.2016.04.010

中图分类号：U441.3

文献标识码：A

文章编号：1672-3953(2016)04-0037-05

An Analysis of the Dynamic Response of the Large-Spanned Continuous Beam-Arch Bridge Induced by a High-Speed Train

Li Guanghui1,Sun Chuan2

(1.4th Engineering Co. Ltd. of the 16th Bureau Group of the Railway Building Corporation of the PRC,Beijing 101400,China;2.The Municipal Construction Investment Holding Company of Shijiazhuang，Shijiazhuang 050051,China)

Abstract:With a certain large-spanned continuous beam-arch bridge as the object of our studies,a 3-dimensional dynamic analysis model for the bridge is established in the light of the finite element software of ANSYS,with the high-speed train simulated as a multi-body system made up of mass, spring and damper.Then,the train-bridge dynamic response of the large-spanned continuous beam-arch bridge is simulated and analyzed,upon the basis of which the effects of different train parameters on the dynamic response of the bridge are explored.The results of our analyses show that the maximum dynamic response of the continuous beam-arch bridge,under the excitation of the high-speed train,occurs when the train moves near the middle of each span; the influence of the train speed on the dynamic response of the bridge is great,while the stiffness of the train spring on the dynamic response of the bridge is relatively small.

Key words:continuous beam-arch bridge;vibration induced by the train;vibration response