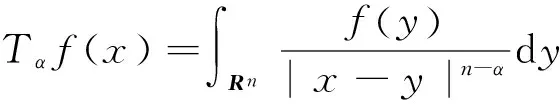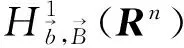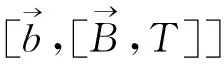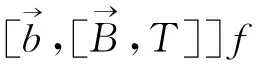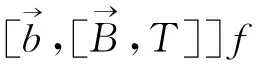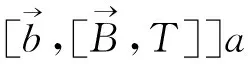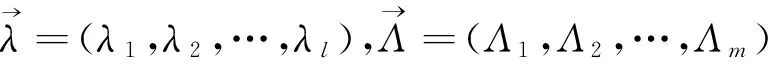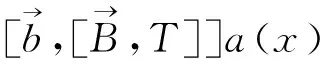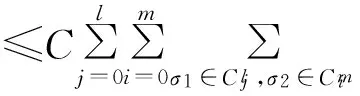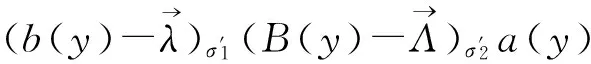一类多线性Calderón-Zygmund算子交换子的估计

王光庆，　周　疆

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐　830046)



一类多线性Calderón-Zygmund算子交换子的估计

王光庆，周疆

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐830046)

摘要：本文研究了由奇异积分算子T与Lipschitz函数bj(j=1,…,l)和BMO函数Bi(i=1，…,m)生成的混合多线性交换子在Lebesgue空间和Hardy空间上的有界性.得到了该多线性交换子是Lp(Rn)到Lq(Rn)和到有界的.

关键词：奇异积分算子；多线性交换子；Lipschitz函数；BMO函数

引言

众所周知，奇异积分算子理论在解决Possion方程解的正则性中起到了很重要的作用，交换子的有界性在调和分析中也扮演很重要的角色([1-8]).交换子的研究由来已久，在976年，Coifman,Rochberg,Weiss在文献[1]引入函数b与Calderón-Zygmund算子T生成的交换子

[b,T]f=bT(f)-T(bf),

多线性交换子是交换的一个自然推广，它由Pérez和Trujillo-González在[3]首先定义，即

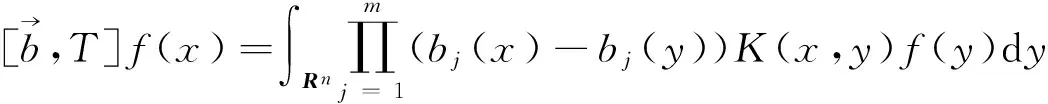
其中T为奇异积分算子

Tf(x)=∫RnK(x,y)f(y)dy,

这里K(x,y)为定义在Rn×Rn{(x,y):x≠y}上的局部可积函数，它满足对所有的x,y,z∈Rn，有

(1)|K(x,y)|≤C|x-y|-n,x≠y，

(1)

存在0<ε≤1，当2|x-z|≤|x-y|时，有

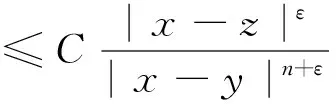
(2)

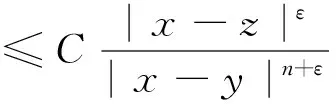
(3)

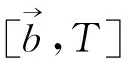
在给出本文相关结果之前，我们先给出该多线性交换子的定义及相关记号.

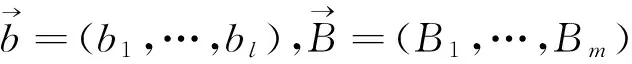
(4)

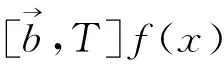
1相关定义和主要结果

定义1.1称函数f(x)属于Lipshitz空间Lipβ(Rn)，0<β≤1，是指函数f(x)满足

定义1.2设f∈Lloc(Rn),Sharp极大函数M#f(x)定义为

定义1.3设0<α

(i) suppa⊂Q=Q(x0,r)={x∈Rn:|x-x0|

(ii) ‖a‖∞≤|Q|-1；

现在我们给出本文的主要结果.

2主要结果证明

定理1.1的证明思路是借用变形的Fefferman和Stein的Sharp极大函数估计，这种思想被许多学者所借鉴(见文献[10-12]).类似地我们先给出Sharp极大函数的估计及相关引理.在以下证明过程中，为书写方便，不妨设‖bj‖Lipβ(Rn)=‖Bi‖BMO(Rn)=1.

引理2.1(见[6])如果0

对所有上式左边有限的函数f成立.

现固定x，设Q是以x为中心，R为半径的球，取λj=(bj)2Q(j=1,2,…,l),Λi=(Bi)2Q(i=1,2,…,m).由于0<δ<1，因而对于任意的α,β∈R，‖α|δ-|β|δ≤|α-β|δ都成立，我们有

=I+II+III.

≤CMα,ε(Tf)(x).

对于II，令f=f1+f2,f1=fχ2Q，则

=II1+II2.

≤CMα,p1f(x).

×f(w)(K(y,w)-K(z,w))dw)dz|dy

对于III的估计，类似于I，

定理1.1的证明由于BMO函数和Lipshitz函数都可以由有界函数来逼近[3]，因此只需证明定理1.1对bj(x)和Bi(x)都是L∞中的函数成立即可.与文献[3]的推理类拟，由引理2.1，引理2.2及Lebegsue微分定理可得，

-[b1,T]((B1(·)-Λ1,j)f(·))(x)

=J1+J2+J3.

对于J2，即当|x-xj|>2rj时，由原子aj的尺寸条件(ii)及消失性(iii)可得

|[b1,T]aj(x)|=|∫Qj(b1(x)-b1(y))K(x,y)aj(y)dy|

≤|∫Qj(b1(x)-b1(xj))(K(x,y)-K(x,xj))aj(y)dy|+|∫Qj(b1(xj)-b1(y))K(x,y)aj(y)dy|

所以，由上式可得

对于J3，由Hølder不等式，考虑到

‖(B1-Λ1,j)f‖1

即(B1(x)-Λ1,j)f(x)∈L1(Rn).对于b1∈Lipα1(Rn)，显然有|[b1，T]((B1(·)-Λ1,j)f(·))(x)|≤CTα1(|(B1(·)-Λ1,j)f(·)|)(x),所以由分数次积分算子Tα1的弱(1，q)有界性知

综上所述，有

再对f的所有的原子分解取下确界，即得结论.

=M1+M2.

则，由上式可得

倒数第三个不等号的估计类似于对引理2.2中II2的估计，最后一个不等号是因为α′<α是显然的，至此定理1.3证明完毕.

参考文献：

[1]COIFMANR，ROCHBERGR，WEISSG.FactorizationtheoremsforHardySpacesinseveralvariables[J]. Ann of Math, 1976,103:611-635.

[2]PÉREZ C. Endpoint estmates for commutators of singular operators[J]. Funct Anal, 1995,128:163-158.

[3]PÉREZ C, TRUJILLO-GONZÉLEZ R. Sharp weighted estimates for multilinear commutators[J]. London Math Soc, 2002,65(3):672-692.

[4]JANSON S. Mean oscillation and commutators of singular integral operator[J]. Ark Math 1978,16:263-270.

[5]CHEN Wengu, HU Guoen. Weak tpye (H1,L1) estimate for a multilinear singular integral operator[J]. Adv in Math(China), 2001,30(1):63-69.

[6]徐景实.多重奇异积分的多线性交换子[J].数学学报，2008，51(5)：1021-1034.

[7]黄政，黄爱武，徐景实.多重奇异积分与Lipschitz函数生成的多线性交换子[J].数学杂志，2011，31(4)：738-748.

[8]STEIN E M. On the functions of littlewood-paley, lusin, and marcinkiewicz[J]. Trans Amer Math Soc, 1958,88(2):430-466.

[9]GENEBASHVILI I, GOGATISHVILI A, KOKILASHVILI, KRBEC M. Weighted theory for integral transforms on spaces of homoogeneous type[J]. Piman Monogr and Surveys in Pure and Appl Math, 92, Longman: Addison-Wesley, 1998.

[10]PÉREZ C, TORRES R. Sharp maximal function estimates for multilinear singular integrals[J]. Harmonic Analysis at Mount Holyoke, Contemporary Mathematics, 2003,320:323-311.

[11]PÉREZ C, TURJILLO-GONZALEZ R. Sharp weighted estimates for vector-valued singular integral operators and commutators[J]. Tohoku Math, 2003,55(1):109-129.

[12]STEIN E. Harmonic analysis[M]. Princeton NJ: Princeton University Press, 2003.

DOI：10.14182/J.cnki.1001-2443.2016.04.005

收稿日期：2015-10-20

基金项目：国家自然科学基金资助项目(11261055)；新疆自然科学基金项目(2011211A005).

作者简介：王光庆(1987-)，男，安徽阜南人，硕士研究生，主要研究方向：调和分析；通讯作者：周疆(1968-)，男，博士，副教授，硕士研究生导师.

中图分类号：O174.2

文献标志码：A

文章编号：1001-2443(2016)04-0331-07

Estimates for a Class of Multilinear Commutators of Calderón-Zygmund Operators

WANG Guang-qing,ZHOU Jiang

(College of Mathermatics and System Sciences, Xinjiang University, Urumqi 830046, China)

Abstract:In this paper, the authors study the boundedness of mixed multilinear commutators ,T]] generated by the BMO functions Bi(i=1,…,m) and Lipschitz functions bj(j=1,…,l) on the Lebesgue space and Hadry space. Then the authors obtain that the multilinear commutators are bounded from Lp(Rn) to Lq(Rn) and (Rn) to (Rn). Furthermore, the authors also prove that when m=1, the multilinear commutators are bounded from H1(Rn) to (Rn).

Key words:singular integral; multilinear commutators; Lipschitz function; BMO function

引用格式：王光庆，周疆.一类多线性Calderón-Zygmund算子交换子的估计[J].安徽师范大学学报：自然科学版，2016，39(4)：331-337.