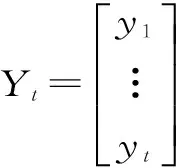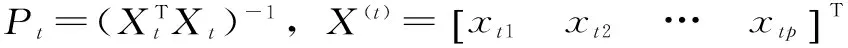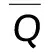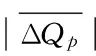产流误差动态系统响应曲线修正方法的应用

束慧连,包为民,2,杨姗姗,刘可新,赵丽平,杨小强

(1.河海大学水文水资源学院,江苏南京210098；2.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京210098)



产流误差动态系统响应曲线修正方法的应用

束慧连1,包为民1,2,杨姗姗1,刘可新1,赵丽平1,杨小强1

(1.河海大学水文水资源学院,江苏南京210098；2.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京210098)

摘要：动态系统响应曲线修正方法(Dynamic System Response Curve,DSRC)是一种基于微分响应的有明确物理意义并且有效的实时修正新方法,属于向误差源头进行修正的方法。通过计算产流的系统响应曲线对产流系列进行修正,实现流量过程的修正。将该方法与新安江模型相结合应用于闽江上游的水吉流域,并将修正效果与递推最小二乘法进行了比较。利用水吉流域29场洪水资料进行模拟和修正,结果表明该方法可以有效提高洪水预报的精度,且其效果优于递推最小二乘法。

关键词：产流误差；动态系统响应曲线；水吉流域

0引言

实时洪水预报作为防洪减灾的非工程措施,有其重要的经济和民生意义。然而,水文模型预报洪水习惯上是采用观测的历史水文资料来确定模型参数,然后用于未来的洪水预报中。但这样的预报方案往往在实时洪水预报中得不到满意的结果。因此,为了提高实时洪水预报的精度,有必要进行实时误差修正。所谓实时洪水预报误差修正就是对在水文模型中没有考虑或是考虑不得当却对预报结果有影响的因素,利用实测信息和其他可利用信息进行实时校正,达到弥补水文模型不足的目的[1]。按修正

内容划分,实时修正方法可以分为：模型误差修正,如自回归模型[2]；模型参数修正,如神经网络算法[3]；模型输入修正,如抗差估计理论[4]；模型状态修正,如卡尔曼滤波方法[5- 6]；综合修正,就是前四种方法的结合[7]。

现有的误差修正方法种类很多[8-12],源于海洋与气象学的数据同化方法也被应用于水文预报的误差修正中[13]。然而,常见的误差修正方法存在各种各样的问题,如没有明确物理意义、预见期的损失、资料不能合理利用等,再加上很多修正方法存在假设条件,当实际情况不能满足假设条件的时候修正效果显然不会理想。例如：卡尔曼滤波方法虽然在修正过程中明确地考虑了模型和资料的不确定性,但是假设条件不易得到满足,应用于分布式水文模型、多参数模型等时计算量大,结构复杂,实时洪水预报难以提供误差修正所需的信息量；自回归模型假设误差序列按时间排序是相关的,但是当预报量发生突变时破坏了相关关系,因此不再适用,修正能力较弱,而且随着预见期的增加修正效果迅速下降；神经网络算法虽然能模拟变量间的非线性关系,但其结构不唯一,且收敛极为缓慢。

动态响应曲线修正方法(Dynamic System Response Curve,DSRC)是一种追溯至误差源头的修正方法,没有采用传统的误差修正方法的修正模式——在预报结果中进行误差修正；而是通过修正用于进行洪水预报的资料达到误差修正的目的。新安江模型分为四个部分,产流误差动态响应曲线修正方法将产流以下的部分作为响应系统,并用差分近似代替微分,得到时段产流量所对应的系统响应曲线,将实测流量和计算流量的差值作为修正信息,用最小二乘估计修正产流过程,达到修正计算流量过程的目的[14]。本文在闽江上游的水吉流域将该误差修正方法与新安江模型相结合,比较分析了修正前后的结果,验证了该方法的可行性和有效性。

1修正方法介绍

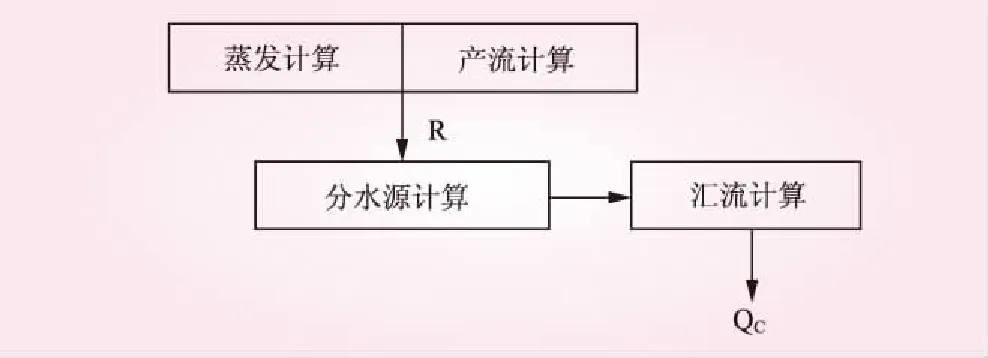
图1　系统示意

新安江模型将模型结构分散为蒸散发计算、产流计算、分水源计算和汇流计算四个层次,汇流计算又包含坡地汇流和河道汇流两部分,坡地汇流计算采用线性水库,河道汇流采用马斯京根分段连续演算。文献[14]提出将产流误差修正的动态系统响应曲线修正方法是将新安江模型的分水源计算和汇流计算这两个层次作为一个系统,如图1所示,系统响应曲线由线性差分近似代替微分得到,修正信息为实测流量系列,采用最小二乘估计原理,对产流量R进行修正,最终实现计算流量QC的修正。

1.1动态系统响应曲线

由文献[14]可知,所谓动态系统响应曲线,就是给某时段的产流量ri增加一个单位的值,用变化后的产流系列带入模型计算得到新的流量过程,这个新的流量过程与改变之前得到的模型计算流量过程Qc相减得到的曲线就是对应ri的系统响应曲线。由于该曲线受到其他时段产流量的影响实时变化,因此称作动态系统响应曲线。文献[14]对其计算过程进行了推导。

方法的关键是U矩阵的求解,即

(1)

式中,RC为模型初始计算径流系列[rc1,…,rcn]；t为时间；θ为模型参数；L为样本长度；Q(RC,θ,t)为模型初始计算流量过程QC。

U矩阵的每一项都可以通过线性差分来代替微分近似求得

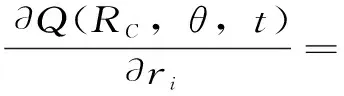
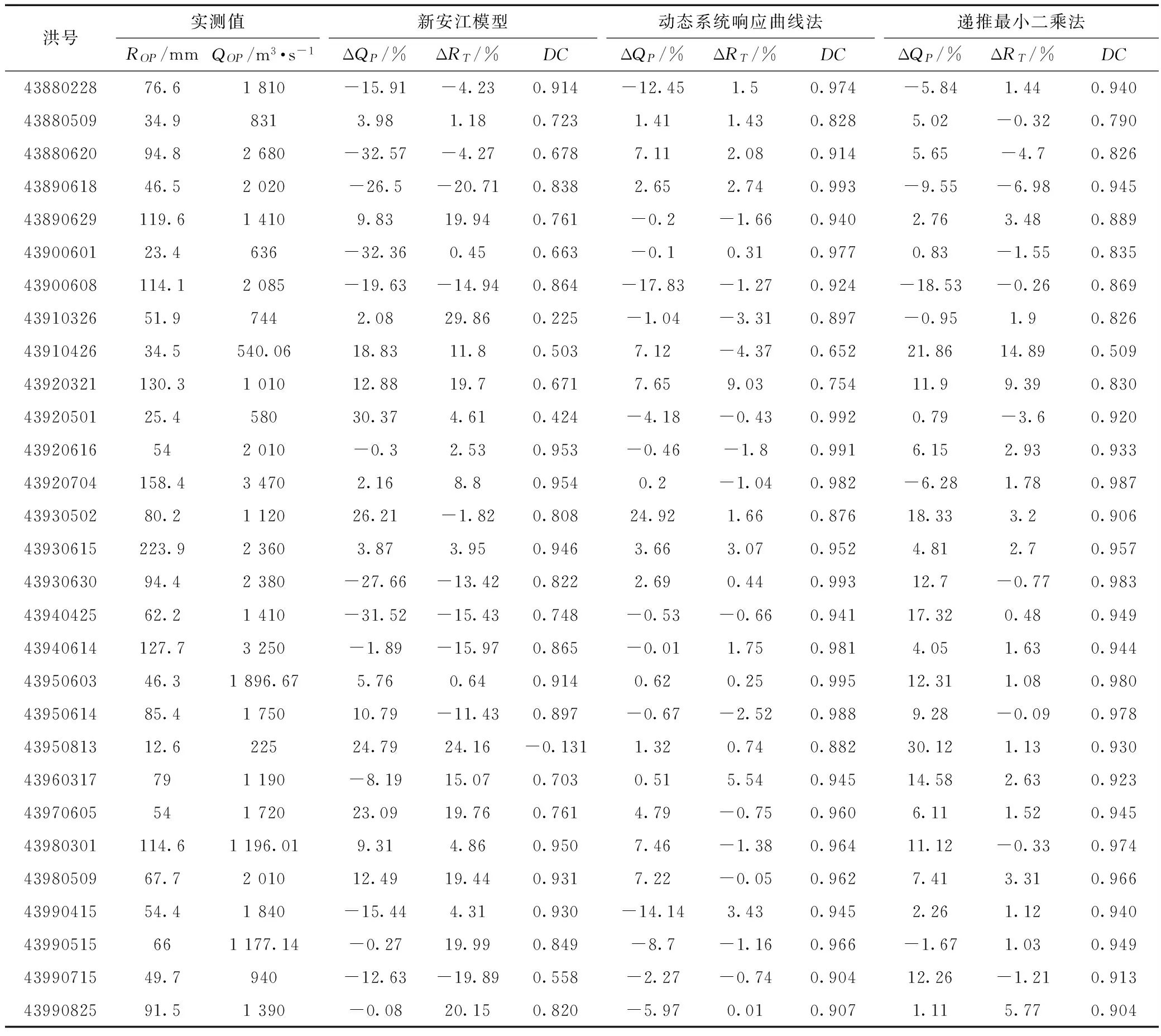
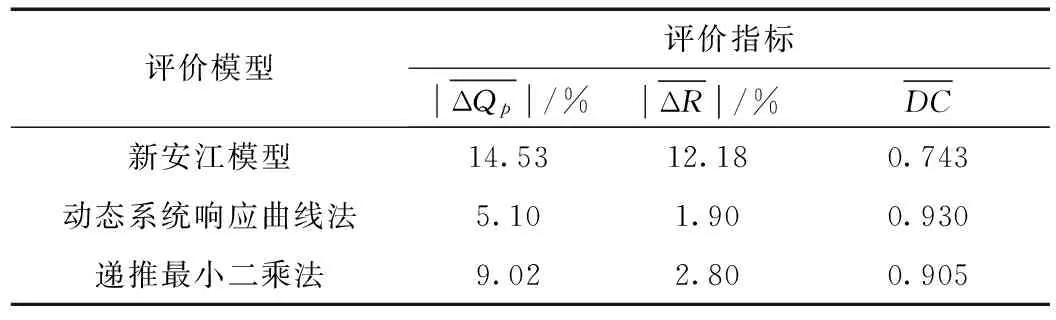
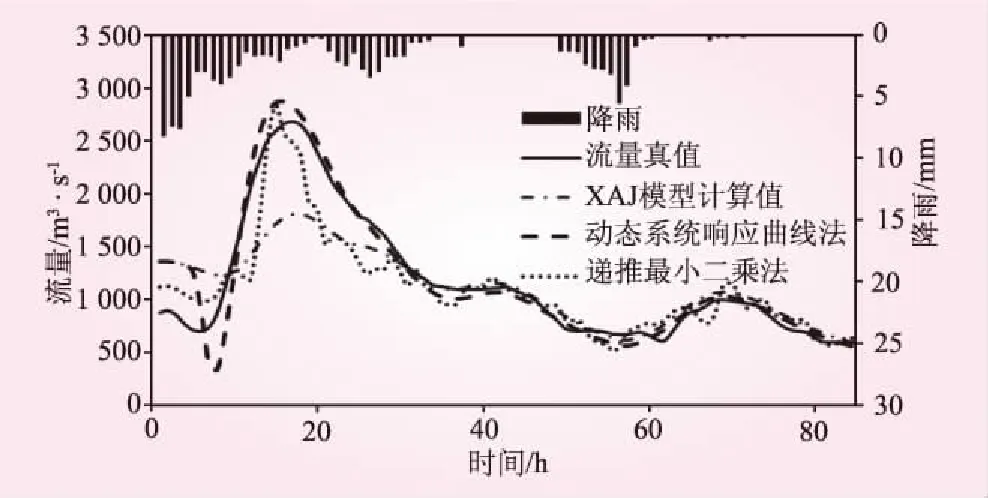
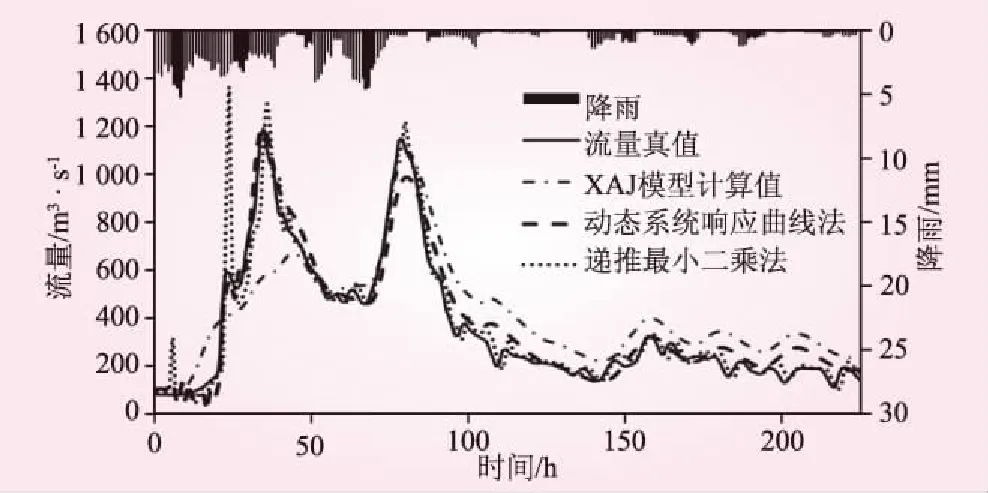
(t

(2)

得到U矩阵的具体计算步骤为：

(1)首先直接通过新安江模型进行计算,得到初始的计算径流过程RC和流量过程QC。

(2)在以计算得到的径流系列的基础上给i时段的径流量增加1个单位值,将变化后的径流系列带入新安江模型的分水源计算和汇流计算中,求得对应的流量过程。

(3)用步骤(2)中得到的流量过程与初始计算流量过程相减,得到对应时段径流的响应曲线,即U矩阵中的第i列。

(4)完成所有列的计算则得到U矩阵。

计算得到U矩阵后,产流量的修正量ΔR通过最小二乘法得到,即

ΔR=(UTU)-1UT(Q(R,θ,L)-Q(RC,θ,t))

(3)

将修正后的产流量R′=RC+ΔR带入新安江模型,计算得到修正后的计算流量过程,可以实现误差修正。

1.2递推最小二乘法

描述时间系列的线性回归模型[7],其观测系列为(x11,x12,…,x1p;y1),(x21,x22,…,x2p;y2),…,(xt1,xt2,…,xtp;yt)。其中,x为自变量；y为因变量；t为时刻；p为模型回归阶数。若已知t时刻之前的自变量和因变量的观测值,要估计t+1时刻的因变量,可根据这些观测信息先用最小二乘法估计出参数,然后再估计y值。递推最小二乘法可以解决当中计算量的问题和随着信息量的增大计算机容量的问题。

将每个观测值带入回归方程

(4)

写成矩阵形式为

Yt=XtCt+Et

(5)

表1水吉流域使用新安江模型的参数

WMUMLMKCBIMCSMEXKGKICGCICSKEXE16320801.350.7900.1613.751.50.450.40.9940.920.7451.99770.2175

注：表中WM为流域平均张力水容量,mm；UM为上土层张力水容量,mm；LM为下土层张力水容量,mm；KC为蒸散发折算系数；B为蓄水容量面积分布曲线指数；IM为不透水面积占全流域面积比例；C为深层蒸散发扩散系数；SM为自由水蓄水容量,mm；EX为自由水蓄水容量面积分布曲线指数；KG和KI分别为自由水蓄水库对地下水和壤中流的日出流系数；CG、CI、CS分别为地下水、壤中流、地面径流；KE和XE为马斯京根法参数,其中KE单位为h。

在t-1时刻和t时刻可得参数的最小二乘估计

(6)

(7)

经过一系列的简化和计算可以得到参数的递推最小二乘估计

(8)

2应用与检验

2.1流域简介

闽江流域处于亚热带季风气候区,雨量丰沛,气候温和。流域多年平均降水量1 724 mm,年内分布不均,年际变化大,其中60%左右的年降水量主要集中在4月～6月,丰水年降雨量是枯水年的2～3倍。受气候的影响,流域内多年平均蒸发量为915.0 mm[15],夏季蒸发量较大,冬季蒸发量较小。

水吉流域地处闽江上游地区,南平以上闽江支流南浦溪流经该流域,流域面积3 767 km2,多年平均气温15～20℃。本文选用水吉流域1988年～1999年之间的资料进行分析,流域年平均降水量为1 820 mm,年平均径流深972.0 mm[16],径流系数大于0.4,属于典型的湿润地区,使用三水源新安江模型进行洪水模拟预报是较为合理的。

水吉流域境内有11个雨量站,分别为：游枫、东坑、浦城、仙阳、高坊、山下、洋源、旧馆、管坦、水吉、外屯,有一个蒸发站,以水吉站作为预报站。

2.2应用检验

本文选用水吉流域1988年～1999年间29场洪水资料,使用新安江模型进行模拟,模型使用的参数采用日模参数率定获得的结果,具体见表1。

验证产流误差的动态响应曲线修正方法的修正效果,具体通过以下3项指标来衡量修正效果：

(1)确定性系数DC

(9)

(2)洪峰相对误差ΔQP

ΔQP=((QCP-QOP)/QOP)×100%

(10)

(3)洪量相对误差ΔQT

ΔQT=((RC-RO)/RO)×100%

(11)

29场洪水修正前和修正后的结果比较及修正效果见表2、表3。43880620和43960317场次洪水的修正结果如图2和图3所示。

表2水吉流域29场洪水实时修正前后计算结果

洪号实测值ROP/mmQOP/m3·s-1新安江模型ΔQP/%ΔRT/%DC动态系统响应曲线法ΔQP/%ΔRT/%DC递推最小二乘法ΔQP/%ΔRT/%DC4388022876.61810-15.91-4.230.914-12.451.50.974-5.841.440.9404388050934.98313.981.180.7231.411.430.8285.02-0.320.7904388062094.82680-32.57-4.270.6787.112.080.9145.65-4.70.8264389061846.52020-26.5-20.710.8382.652.740.993-9.55-6.980.94543890629119.614109.8319.940.761-0.2-1.660.9402.763.480.8894390060123.4636-32.360.450.663-0.10.310.9770.83-1.550.83543900608114.12085-19.63-14.940.864-17.83-1.270.924-18.53-0.260.8694391032651.97442.0829.860.225-1.04-3.310.897-0.951.90.8264391042634.5540.0618.8311.80.5037.12-4.370.65221.8614.890.50943920321130.3101012.8819.70.6717.659.030.75411.99.390.8304392050125.458030.374.610.424-4.18-0.430.9920.79-3.60.92043920616542010-0.32.530.953-0.46-1.80.9916.152.930.93343920704158.434702.168.80.9540.2-1.040.982-6.281.780.9874393050280.2112026.21-1.820.80824.921.660.87618.333.20.90643930615223.923603.873.950.9463.663.070.9524.812.70.9574393063094.42380-27.66-13.420.8222.690.440.99312.7-0.770.9834394042562.21410-31.52-15.430.748-0.53-0.660.94117.320.480.94943940614127.73250-1.89-15.970.865-0.011.750.9814.051.630.9444395060346.31896.675.760.640.9140.620.250.99512.311.080.9804395061485.4175010.79-11.430.897-0.67-2.520.9889.28-0.090.9784395081312.622524.7924.16-0.1311.320.740.88230.121.130.93043960317791190-8.1915.070.7030.515.540.94514.582.630.9234397060554172023.0919.760.7614.79-0.750.9606.111.520.94543980301114.61196.019.314.860.9507.46-1.380.96411.12-0.330.9744398050967.7201012.4919.440.9317.22-0.050.9627.413.310.9664399041554.41840-15.444.310.930-14.143.430.9452.261.120.94043990515661177.14-0.2719.990.849-8.7-1.160.966-1.671.030.9494399071549.7940-12.63-19.890.558-2.27-0.740.90412.26-1.210.9134399082591.51390-0.0820.150.820-5.970.010.9071.115.770.904

表3水吉流域29场洪水实时修正平均修正效果

评价模型评价指标ΔQp/%ΔR/%DC新安江模型14.5312.180.743动态系统响应曲线法5.101.900.930递推最小二乘法9.022.800.905

图2　43880620场次洪水的误差修正结果

图3　43960317场次洪水的误差修正结果

从图2、3和表2、3可以看出：采用基于动态系统响应曲线的产流误差修正方法之后,洪峰相对误差、洪量相对误差均有所减小,确定性系数均有所提高,平均修正效果也好于递推最小二乘法。计算过程中发现,采用递推最小二乘法修正时会出现时刻流量值突涨的现象。如43960317场次的洪水,修正后虽然各项指标有所提高但洪峰偏大且峰现时间提前,实际上修正后并不符合要求。而动态系统响应曲线方法则没有这一缺点。从后者模拟效果得到了明显的提升可以认为,产流误差动态响应曲线修正方法可以有效应用于水吉流域。

3结论

产流误差动态系统响应曲线修正方法是一种新的实时校正方法,其物理意义明确、结构简明,既不损失预见期也不增加模型的参数个数,且能有效保证预报精度。在水吉流域的应用进一步验证了该方法的合理性和实用性,将29场洪水的洪峰平均相对误差从14.53%降低到5.10%,洪量平均相对误差从12.18%降低到1.90%,平均确定性系数从0.743提高到0.930。与递推最小二乘法比较也体现了其优越性,整体修正效果相对较好。虽然该方法也存在问题,如U矩阵的稳定性问题等,但值得在更多流域进行应用验证推广和改进,以推进实时洪水预报误差修正方法的发展。

参考文献：

[1]包为民. 水文预报[M]. 北京: 中国水利水电出版社, 2006.

[2]周轶, 李致家. 改进最小二乘递推算法的洪水预报应用研究[J]. 水力发电, 2006, 32(8)： 14- 16.

[3]覃光华, 丁晶. 基于人工神经网络的卡尔曼滤波实时校正技术[J]. 水力发电, 2002(11)： 9- 12.

[4]包为民, 嵇海祥, 胡其美, 等. 抗差理论及在水文学中的应用[J]. 水科学进展, 2003, 14(4)： 528- 532.

[5]WU Xiaoling, WANG Chuanhai, CHEN Xi, et al. Kalman Filtering Correction in real-time forecasting with hydrodynamic model[J]. Journal of Hydrodynamics, Ser. B, 2008, 20(3): 391- 397.

[6]KOMMA J, BLÖSCHL G, RESZLER C. Soil moisture updating by Ensemble Kalman Filtering in real-time flood forecasting[J]. Journal of Hydrology, 2008, 357(3): 228- 242.

[7]瞿思敏, 包为民. 实时洪水预报综合修正方法初探[J]. 水科学进展, 2003, 14(2)： 167- 171.

[8]HINO M. Runoff forecasts by linear predictive filter[J]. Journal of the Hydraulics Division, 1970, 96(3): 681- 702.

[9]BIONDI D, De LUCA D L. A Bayesian approach for real-time flood forecasting[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2012, 42/44: 91- 97.

[10]HSU M H, FU J C, LIU W C. Flood routing with real-time stage correction method for flash flood forecasting in the Tanshui River, Taiwan[J]. Journal of Hydrology, 2003, 283(1): 267- 280.

[11]MADSEN H, SKOTNER C. Adaptive state updating in real-time river flow forecasting—A combined filtering and error forecasting procedure[J]. Journal of Hydrology, 2005, 308(1): 302- 312.

[12]PAGANO T C, WANG Q J, HAPUARACHCHI P, et al. A dual-pass error-correction technique for forecasting streamflow[J]. Journal of Hydrology, 2011, 405(3): 367- 381.

[13]YU Z, LIU D, LÜ H, et al. A multi-layer soil moisture data assimilation using support vector machines and ensemble particle filter[J]. Journal of Hydrology, 2012, 475: 53- 64.

[14]司伟, 包为民, 瞿思敏. 洪水预报产流误差的动态系统响应曲线修正方法[J]. 水科学进展, 2013, 24(004): 497- 503.

[15]林虹. 闽江流域实时洪水预报系统模型研究[D]. 南京： 河海大学, 2005.

[16]张章新. 闽江流域水文特性分析[J]. 水文, 2000, 20(6): 55- 58.

(责任编辑陈萍)

收稿日期：2015- 06- 23

基金项目：国家自然科学基金面上项目(51279057/41371048/51479062)；国家自然科学基金重大项目(51190090)；国家自然科学基金重大项目子项目(51190091)；中央高校基本科研业务费专项资金资助(2014B35314)

作者简介：束慧连(1989—),女,江苏盐城人,硕士研究生,主要从事水文物理规律模拟、水文预报方面研究．

中图分类号：P338(257)

文献标识码：A

文章编号：0559- 9342(2016)04- 0022- 05

Application of Runoff Error Correction Based on Dynamic System Response Curve

SHU Huilian1, BAO Weimin1,2, YANG Shanshan1, LIU Kexin1, ZHAO Liping1, YANG Xiaoqiang1

(1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China; 2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, Jiangsu, China)

Abstract:The correction method of Dynamic System Response Curve (DSRC) is a new real-time correction method that is based on differentiation and is with clear physical meaning. This method can trace back to the source of error. The dynamic system response curve of runoff is calculated and then it is used to correct the runoff, and eventually, the correction of flood process is realized. To verify the correction effectiveness of DSRC method, it is combined with the Xin’anjiang model and is tested in Shuiji Basin of Minjiang River, and the method is also compared to the recursive least square method. Total 29 floods in Shuiji Basin are calculated and corrected, and the results of correction show that the correction method of dynamic system response curve has a remarkable effect in improving the accuracy of flood forecasting and it is more effective than the recursive least square method．

Key Words:runoff error; dynamic system response curve; Shuiji Basin