MPI并行的节点大地电磁三维有限元正演

马　驹， 肖调杰*， 王　赟

(1. 中国科学院　地球化学研究所，贵阳　550002；2.中国科学院大学，北京　100049；3. 中国科学院　地质与地球物理研究所，北京　100029)



MPI并行的节点大地电磁三维有限元正演

马驹1,2， 肖调杰1,2*， 王赟1,3

(1. 中国科学院地球化学研究所，贵阳550002；2.中国科学院大学，北京100049；3. 中国科学院地质与地球物理研究所，北京100029)

摘要：用fortran语言编程实现了有限元三维大地电磁正演，通过层状介质模型、二维棱柱体模型及三维低阻体模型结果的对比，验证了所编写程序的正确性。首先通过加入第一类边界条件，减少了最终求解方程组的维数，同时对系数矩阵的存储采用非零存储技术，大大降低了对计算机内存的需求；最后在串行程序的基础上，基于MPI实现了频点间的并行，并对一个三维模型进行计算，并行后开启4进程时加速比达到了2.328，有效地减少了所需时间。

关键词：大地电磁； 三维； 正演； 并行； MPI

0引言

自上世纪70年代以来很多学者都对电磁三维正演进行了研究，主要有积分方程法[1-3]、有限差分法[4-6]及有限单元法[7]。Wannamaker[2]于对积分方程法的应用于三维大地电磁正演的进展进行了论述；Mackie等[4]讨论了有限差分法在三维大地电磁模拟中的应用，并与前人的积分方程法结果进行了对比。相对而言，有限元法更适用于地形复杂情况的三维电磁模拟， Thohru Mogi[7]利用二次场实现了三维正演，避免了电场在不连续界面不连续的问题，并通过模型验证了其正确性； Yuji Mitsuhata等[8]实现了电矢量位磁标量位三维有限元正演，效果不错； Puzyrev等[9]给出了基于磁矢量势和电标量势的并行频率域节点有限元法；Silva等[10]给出了基于多波前法的三维矢量有限元数值模拟结果。

目前，在地球物理学中，并行计算已经得到越来越多的关注和应用，当前主要有两种并行编程模式[11]，①基于消息传递型的进程级并行编程模式MPI(Message Passing Interface)；②共享内存型的线程级并行编程模式OpenMP(Open Multi-Processing)。相对于OpenMP ，这里选取移植性更强的MPI并行模式。作者基于有限单元法用fortran语言编程实现了大地电磁三维正演，采用六面体剖分，单元内进行线性插值，最后形成的总体刚度矩阵是一大型稀疏、带状、对称但不正定的复系数矩阵[12]，最后形成的系数矩阵采用CSR(Compressed Sparse Row format)非零存储以节省内存空间，解方程采用高效、收敛速度快的双共轭梯度法，同时采用直接法加入第一类边界条件，降低了系数矩阵的维数[13]；最后在串行程序基础上，基于MPI实现了频点间的并行计算，有效地节省了时间。

1三维正演基本理论

1.1边值问题

取时间因子为e-iωt，则由Maxwell方程组可得式(1)。

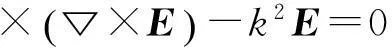
(1)

其中：E是电场；k2=iωμσ+ω2εμ；ω为角频率；μ是介质的导磁系数；σ是介质的电导率；ε是介质的介电常数。

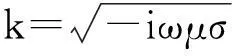
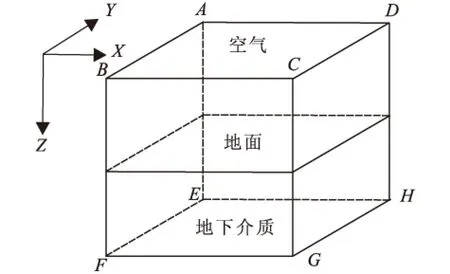
图1　三维大地电磁正演模型示意图Fig．1　Model of 3D magnetotelluric sounding

1.2六面体剖分

母单元是一个边长为2的正方体，取8个角点为节点，编号及坐标如图2(a)所示，图2(b)为子单元。

图2　六面体剖分单元Fig．2　Division of hexahedron(a)母单元；(b)子单元

构造形函数为式(2)。

(2)

其中：ξi、ηi、γi是节点i在母单元中的坐标。

1.3总体系数矩阵

由广义变分原理建立泛函，如式(3)所示。

k2E·E]dV

(3)

加入散度条件：

1)空气中散度条件为▽·E=0。

2)介质中散度条件为▽·σE=0，得到式(4)。

在式(4)中加入边界条件，进行离散，然后在单元内插值，再将积分转换为线性函数，最后得到总体刚度矩阵，进而得到线性方程组：

KE=0

(5)

解方程即可得各电场分量，进而可根据电场分量计算得到各磁场分量。

1.4张量阻抗计算

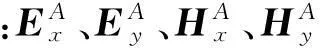
(6)

(7)

(8)

(9)

式(7)定义的响应称为XY模式响应，式(8)定义的响应称为YX模式响应。进一步便可计算得到相应的视电阻率和相位如式(10)所示。

(10)

(i=x,y;j=x,y)

2模型计算

分别对层状介质模型、二维模型及三维模型进行了计算并对比。

2.1三层层状状介质模型

三层层状介质模型如图3所示。我们用解析解与三维数值解进行了对比，计算频点为1 000 Hz、100 Hz、10 Hz、1 Hz、0.1 Hz、0.01 Hz与0.001 Hz共7个频点。视电阻率曲线见图4，相位曲线见图5。其中视电阻率最大相对误差为0.282 8%，相位最大相对误差为0.048 23%，表明三维数值模拟结果与解析解拟合得非常好。

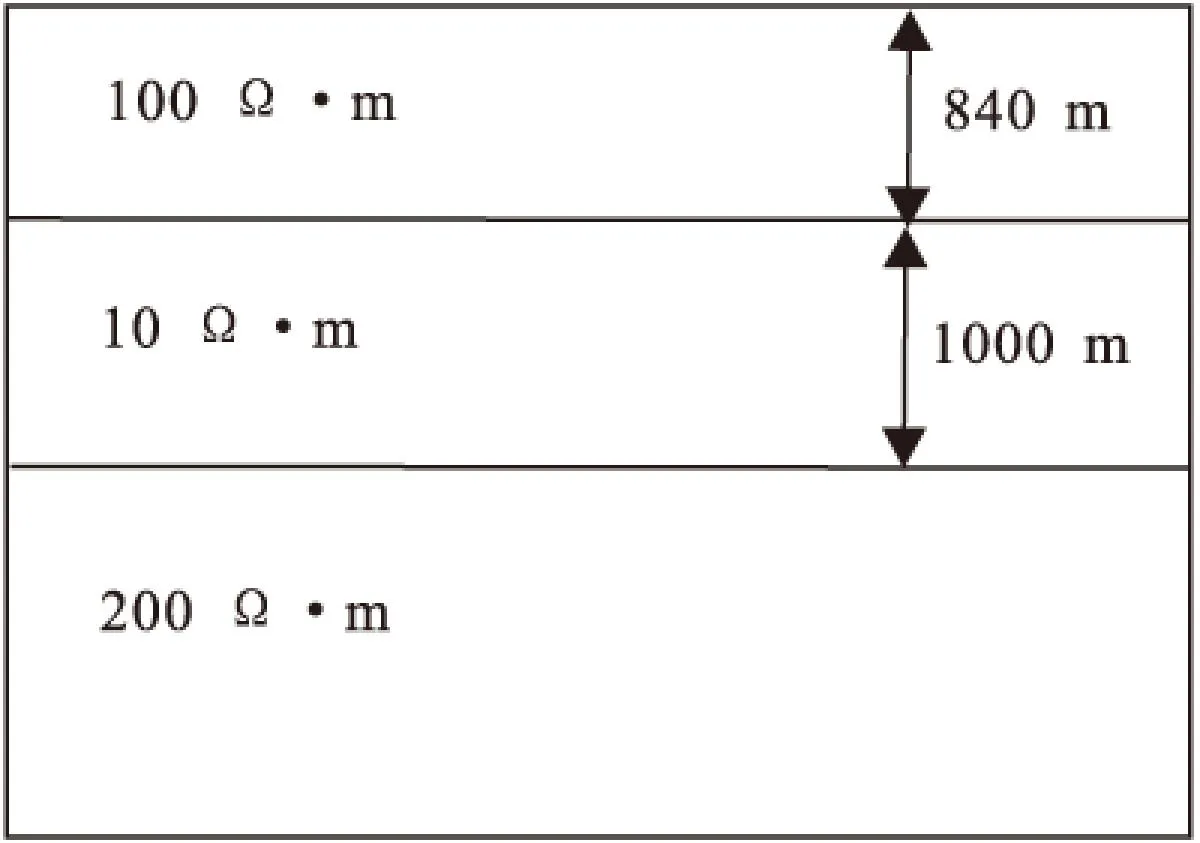
图3　三层层状介质模型Fig．3　The model of layered media

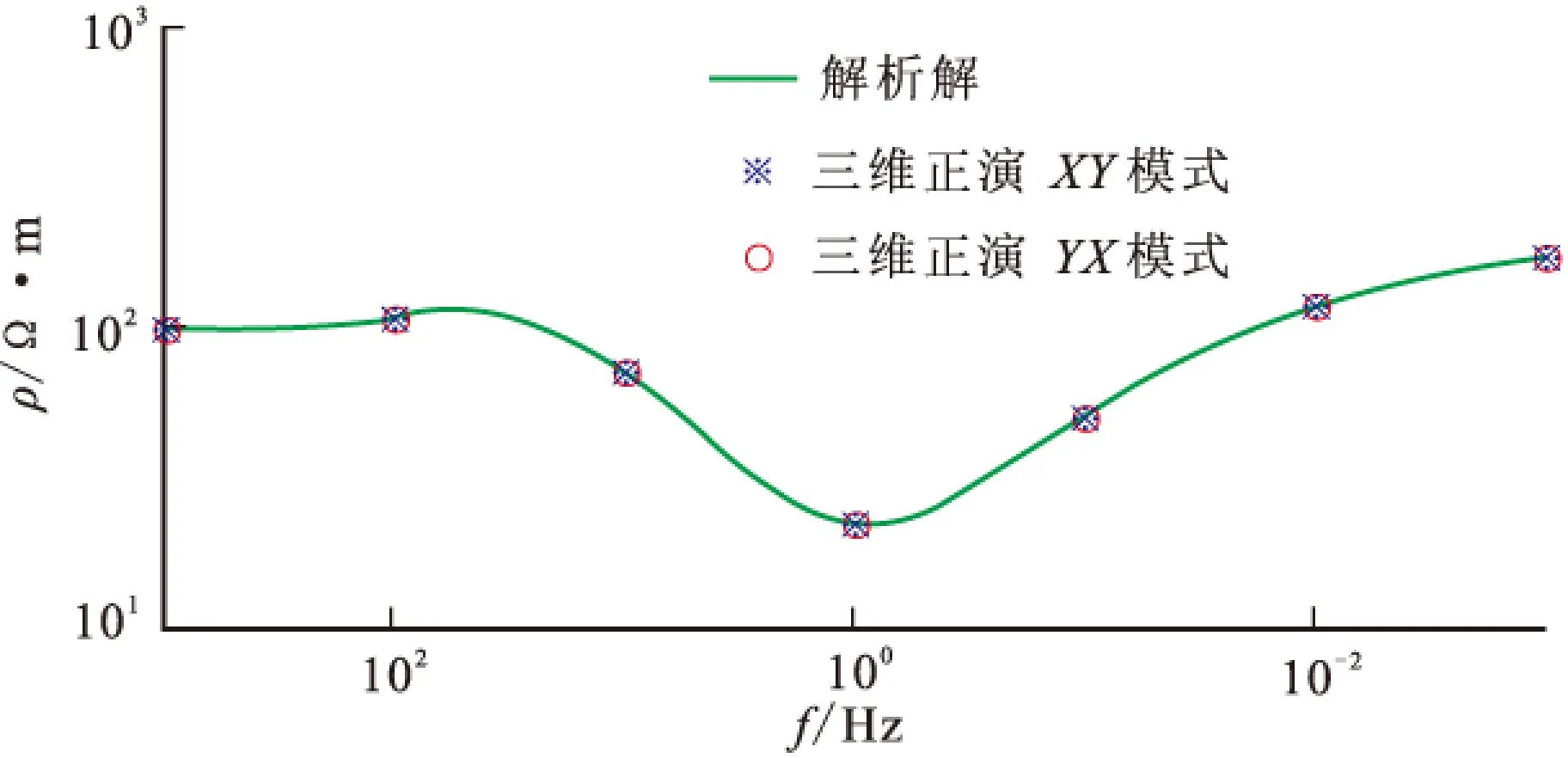
图4　三层层状介质三维大地电磁正演视电阻率值与解析解的对比Fig．4　The comparison of apparent resistivity between analytical results and numerical results

图5　三层层状介质三维大地电磁正演相位与解析解的对比Fig．5　The comparison of phase between analytical results and numerical results

2.2二维棱柱体模型

二维棱柱体模型如图6所示，棱柱体走向为Y方向，电阻率为10 Ω·m，几何尺寸为3 000 m×6 000 m ，顶面埋深为3 000 m ，围岩电阻率为100 Ω·m。

我们分别用二维有限单元法和三维有限单元法对该模型进行了计算，计算频点为3 Hz、1 Hz及0.5 Hz三个频点。将三维YX模式、XY模式分别与二维TE模式、TM模式进行了对比，图7为三维YX模式与二维TE模式对比，二者结果拟合得非常好，最大相对误差为0.378 7%，图8为三维XY模式与二维TM模式对比，二者结果拟合得很好，最大相对误差为1.288 8%。

图6　低阻体模型Fig．6　Geometry of 2D prism model

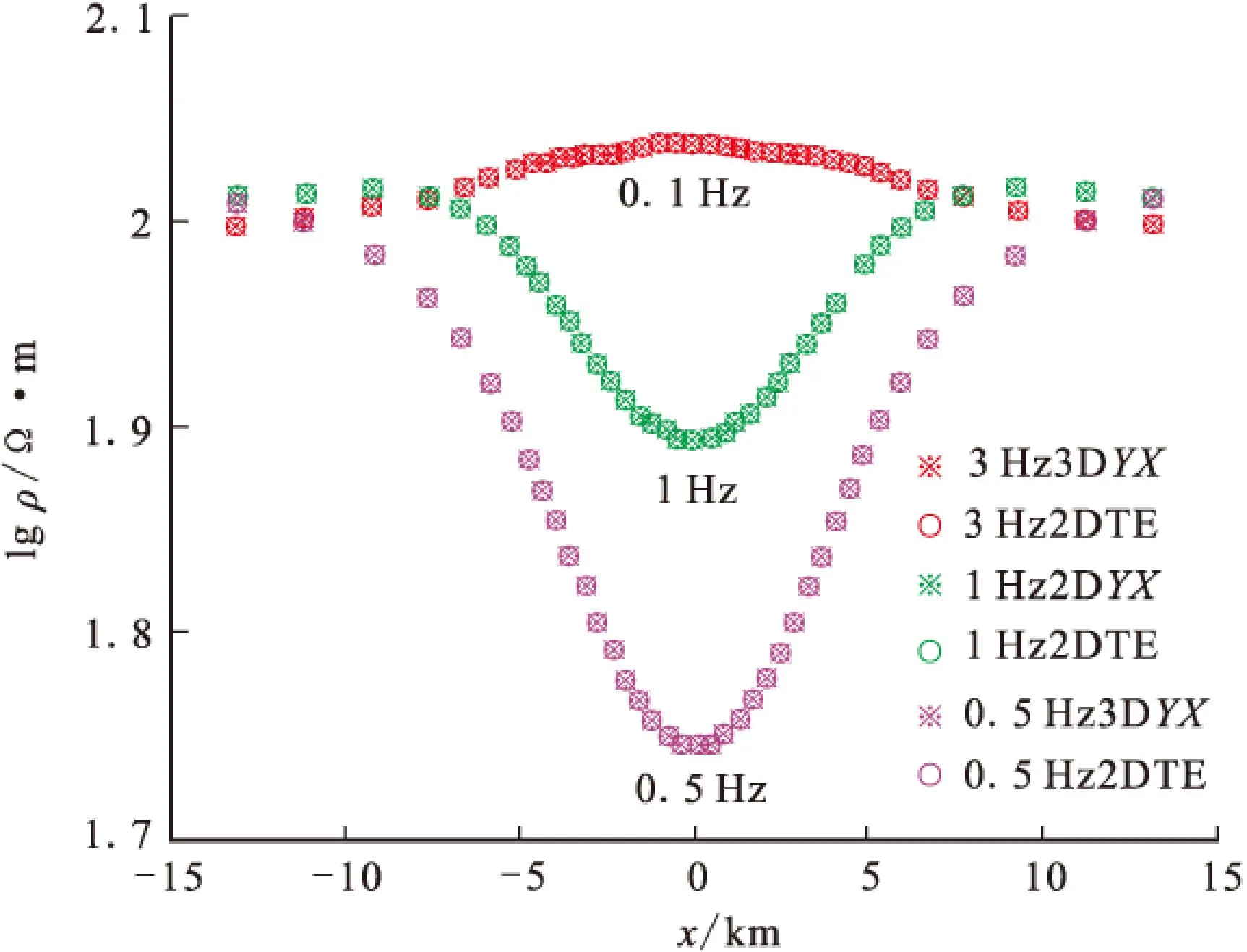
图7　YX模式与TE模式对比Fig．7　The comparison of YX mode and TE mode

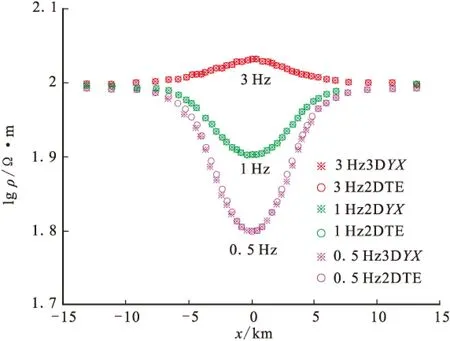
图8　XY模式与TM模式对比Fig．8　The comparison of XY mode and TM mode

2.3三维棱柱体

三维模型采用文献[6]的三维棱柱体模型，如图9所示，三维棱柱体尺寸为6 000 m×6 000 m×3 000 m，电阻率为10 Ω·m，顶面埋深为3 000 m，围岩电阻率为100 Ω·m。计算频点为3 Hz、1 Hz及0.1 Hz共3个频点，将YX模式、XY模式分别与参考文献[6]中的数值模拟结果进行了对比，YX模式对比如图10所示，可以看到不管是XY模式还是YX模式，3 Hz及1 Hz时二者拟合很好， 0.1 Hz时曲线形态基本一致，值有所差别，但最大相对误差都在5%以内。

图9　三维低阻体模型Fig．9　Geometry of 3D prism model

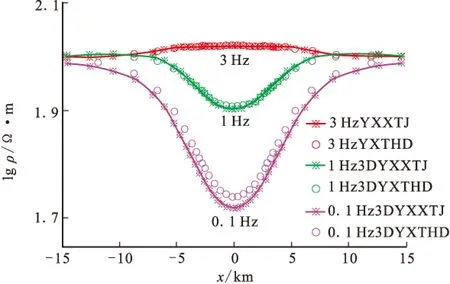
图10　YX模式视电阻率对比Fig．10　The apparent resistivity of YX mode

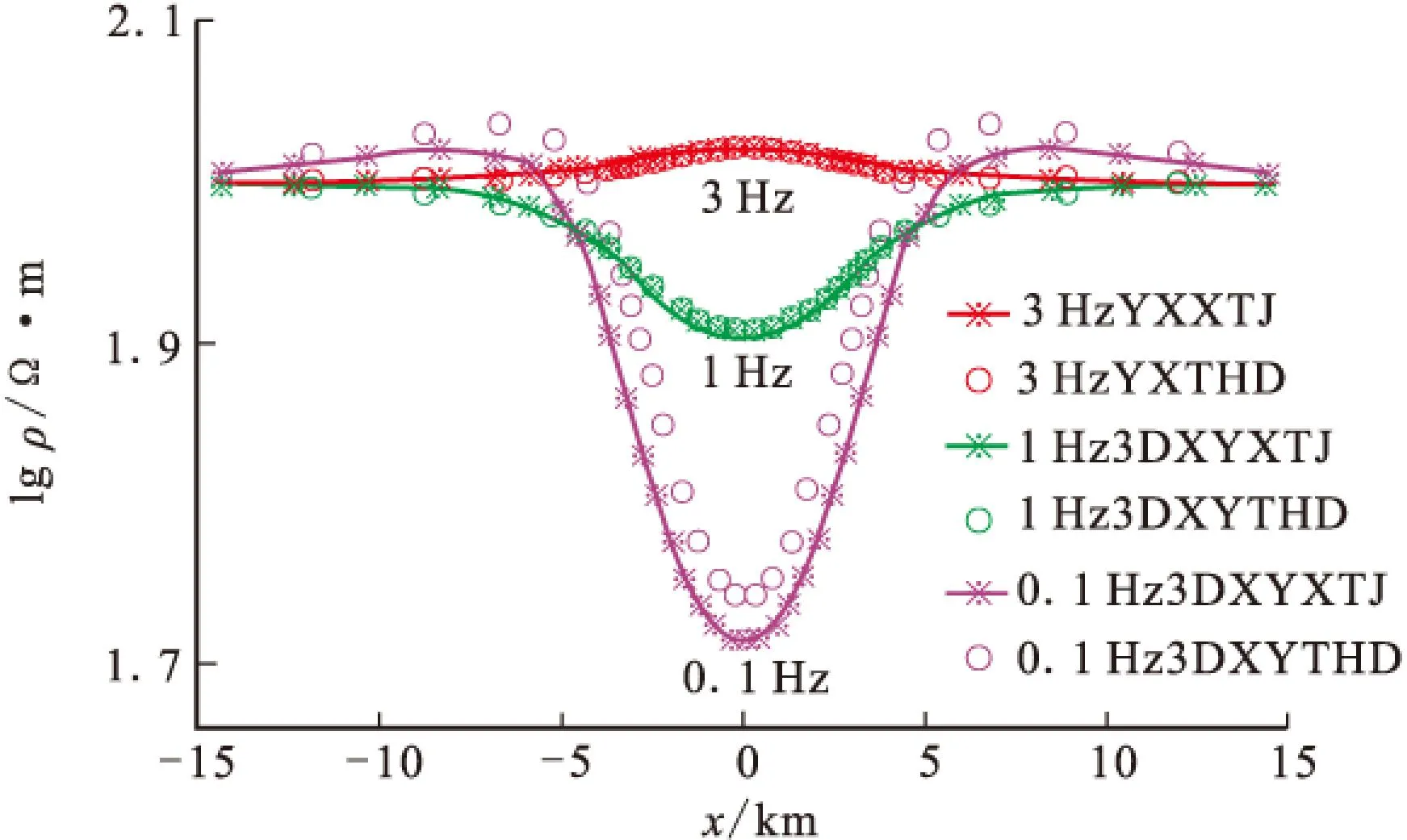
图11　XY模式视电阻率对比Fig．11　The apparent resistivity of XY mode

通过以上三个模型的计算与对比，表明三维有限元数值模拟是准确可靠的。

3MPI并行计算

3.1MPI并行实现

MPI(Massage Passing Interface)是目前最为通用的并行编程方式之一，也是分布式并行系统的主要编程环境，作者在实现了大地电磁三维正演基础上，基于MPI实现了频点间的并行，MPI并行算法伪代码如下：

PROGRAM MT3DForwardFEM

USE MPI !调用MPI模块

……

!初始化MPI系统；得到所有参加运算的进程的个数，放NUMPROCS中；得到当前正在运行的进程的标识号，放在MY_RANK中

CALL MPI_INIT(IERR)

CALL MPI_COMM_SIZE(MPI_COMM_WORLD,NUMPROCS,IERR)

CALL MPI_COMM_RANK(MPI_COMM_WORLD,MY_RANK,IERR)

……

!为每个进程都分配长度一样的一维数组用来存储每个进程得到的结果，FN是频点数，!UNX是测点数，在这里统一分配(FN/NUMPROCS+1)*UNX大小，后面对结果再进行一下处理，收集结果时就可以用MPI_GATHER()函数而不必使用麻烦的MPI_GATHERV()函数

ALLOCATE(RESXY((FN/NUMPROCS+1)*UNX))

ALLOCATE(APHXY((FN/NUMPROCS+1)*UNX))

ALLOCATE(RESYX((FN/NUMPROCS+1)*UNX))

ALLOCATE(APHYX((FN/NUMPROCS+1)*UNX))

……

IF(MY_RANK==0)THEN

读取电阻率、坐标等信息

END IF

CALL MPI_BCAST()!广播主进程读取的输入信息

……

DO

FI=MY_RANK+1,FN,NUMPROCS

… …

调用子程序计算形成总体系数矩阵、加入边界条件值、解方程、计算视电阻率及相位

… …

END DO

……

!进程同步后收集各进程上的结果

CALL MPI_BARRIER(MPI_COMM_WORLD,IERR)

!在主进程上收集XY模式及YX模式的视电阻率及相位

CALL MPI_GATHER()

CALL MPI_GATHER()

CALL MPI_GATHER()

CALL MPI_GATHER()

……

写入结果

……

CALL MPI_FINALIZE(IERR) !退出MPI系统

END PROGRAM MT3DFowardFEM

程序在采用MPI_GATHER()函数的情况下实现了对任意频点数的并行化。

3.2并行效率提升评价

对一个低阻体模型进行了并行计算，模型如图12所示，低阻体尺寸为800 m×800 m×1 050 m，顶面埋深为350 m，电阻率为40 Ω·m，围岩电阻率为100 Ω·m。并行程序可以不加修改的在其他并行平台上运算，我们在四核机上进行运算，配置为Intel(R) CoreTMi7-4790 CPU，主频为3.6 GHz，内存16 G，64位操作系统。从0.01 Hz～1 000 Hz范围内按对数均匀取26个频点进行并行计算，网格大小为42×42×23。并行计算时间见表1，图13与图14分别反映了开启不同进程时加速比及效率的变化，其中，并行加速比=串行时间/并行计算时间；并行效率=并行加速比/并行进程个数。

对图13、图14及表1进行分析：当开启进程数增加时，并行效率降低；随着进程数量的增加，并行加速比继续增大，但并行效率反而下降，这是因为随着进程数的增加，用于进程间通信的时间所占比例逐渐增大；1个进程的并行计算时间比串行时间长，这是因为采用并行需要额外的开销，总的看来，并行效果还是很明显的，当开启4个进程时达到了2.3的加速比。

图12　三维低阻体模型Fig．12　Geometry of 3D model

图13　开启进程数量不同时的加速比Fig．13　The speed-up with different 　numbers of threads

图14　开启进程数量不同时的效率Fig．14　The efficiency with different 　number of threads

3.3MPI并行计算结果

由于并行计算并没有改变算法，因此并行结果和串行结果一样。取X=-1 400 m、-800 m、-400 m、-200 m、0 m、200 m、400 m、800 m、1 400 m 测线的纵向剖面图，由于所得结果是关于X=0 m对称的，因此在这里只展示X=0 m、200 m、400 m、800 m、1 400 m处的剖面图，视电阻率剖面图如图15所示，相位剖面图如图16所示。

图15　视电阻率纵向切片图Fig．15　The cross-section of apparent resistivity with X=0 m,200 m,400 m,800 m,1 400 m respectively(a)x=0 k m;(b)x=0.2 km;(c)x=0.4 km; (d)x=0.8 km; (e)x=1.4 km

图16　相位纵向切片图Fig．16　The cross-section of phase with X=0 m,200 m,400 m,800 m,1 400 m respectively(a)x=0 km;(b)x=0.2 km;(c)x=0.4 km; (d)x=0.8 km; (e)x=1.4 km

取X=0 km处的二维模型进行TE模式正演，三维时X=0 km处的剖面图与二维TE模式剖面图对比,如图17、图18所示。

从图17及图18可看出，三维X=0 km处视电阻率图及相位图都分别与二维TE模式的视电阻率图和相位图相似但并不完全相同。需要考虑到三维正演时用的是三维低阻体，并不是二维模型，而二维本身是对实际情况的近似。

4结论及建议

1)三个模型的计算对比充分说明了算法和程序是可靠及有效的。

2)基于MPI实现了三维大地电磁频点间的并行，有效地减少了计算时间。

3)试验中采用乘大数法加入第一类边界条件有时会得到错误结果，可以进一步研究。

4)辅助场的求取对最后结果影响较大，如何求得高精度的辅助场很值得研究。

感谢：

谭捍东教授提供的三维模型数值模拟结果，在此表示感谢。

图17　三维X=0 km处剖面图与二维TE模式视电阻率剖面图Fig．17　The cross-section of apparent resistivity, the left is the section of 2D with TE model and the right is X=0 km section of 3D(a)二维TE模式视电阻率剖面图；(b)三维X=0处视电阻率剖面图

图18　相位剖面图Fig．18　The cross-section of phase(a)二维TE模式相位剖面图；(b)三维X=0处相位剖面图

参考文献：

[1]TING S C,HOHMANN G W.Integral equation modeling of three-dimensional magnetotelluric response [J].Geophysics,1981,46(2):182-197.

[2]WANNAMAKER P E.Advances in three-dimensional magnetotelluric modeling using integral equations [J].Geophysics,1991,56(11):1716-1728.

[3]WANNAMAKER P E,HOHMANN G W,WARD S H.Magnetotelluric responses of three-dimensional bodies in layered earths[J].Geophysics,1984,49(9):1517-1533.

[4]MACKIE R L,MADDEN T R,WANNAMAKER P E.Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions [J]. Geophysics,1993,58(2):215-226.

[5]MACKIE R L,SMITH J T,MADDEN T R.Three-dimensional electromagnetic modeling using finite difference equations:The magnetotelluric example[J].Radio Science,1994,29(4):923-935.

[6]谭捍东,余钦范,BOOKER J.大地电磁法三维交错采样有限差分数值模拟[J].地球物理学报,2003,46(5):705-715.

TAN H D,YU Q F,BOOKER J.Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J].Chinese Journal of Geophysics,2003,46(5):705-715.(In Chinese)

[7]MOGI T.Three-dimensional modeling of magnetotelluric data using finite element method[J].Journal of applied geophysics,1996,35(2):185-189.

[8]MITSUHATA Y,UCHIDA T.3D magnetotelluric modeling using the T-Ω Ω finite-element method[J].Geophysics,2004,69(1):108-119.

[9]PUZYREV V,KOLDAN J,DE LA PUENTE J,et al.A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling[J].Geophysical Journal International,2013,193(2):678-693.

[10]SILVA N V D,MORGAN J V,MACGREGOR L,et al.A finite element multifrontal method for 3D CSEM modeling in the frequency domain[J].GEOPHYSICS,2012,77(2):E101-E115.

[11]颜小洋,张伟文,布社辉,等.基于MPI/OPENMP混合编程的三维粒子模拟并行优化[J].华南理工大学学报：自然科学版,2012,40(4):71-78.

YAN X Y,ZHANG W W,BU S H,et al.Parallel Optimization of Three-Dimension Particle Simulation Based on Mixed MPI/OPENMP Programming[J].Journal of South China University of Technology (Natural Science Edition),2012,40(4):71-78.(In Chinese)

[12]童孝忠.大地电磁测深有限单元法正演与混合遗传算法正则化反演研究[D].长沙：中南大学,2008.

TONG X Z.Research of forward using finite method and regularized inversion using hybrid genetic algorithm in Magnetotellurics sounding[D].Changsha:Central South University,2008.(In Chinese)

[13]JIN J.The finite element method in electromagnetics[M].John Wiley & Sons,2014.

收稿日期：2015-04-13改回日期：2015-07-23

基金项目:国家科技973项目(2014CB440905)；国家重点实验室“十二五”项目群(SKLODG-ZY125-01)

作者简介：马驹(1990-)，男，硕士，主要从事大地电磁数值模拟研究，E-mail:maju_cug08@163.com。 *通信作者：肖调杰(1991-),男,硕士,从事大地电磁数值模拟，E-mail:xiaotiaojie@mail.gyig.ac.cn。

文章编号：1001-1749(2016)03-0289-08

中图分类号：P 631.3

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.03.01

Three dimensional modeling of magnetotelluric data using finite element method and MPI parallel computation

MA Ju1，2, XIAO Tiao-jie1，2*, WANG Yun1,3

(1. Institute of Geochemistry, Chinese Academy of Sciences, Guiyang550002, China;2.University of Chinese Academy of Sciences,Beijing100049,China;3. Institute of Geology and Geophysics, Chinese Academy of Science, Beijing100029, China)

Abstract:This paper deals with the forward modeling of three-dimensional (3D) magnetotelluric problem by using the finite element method with fortran language. The validity of this FEM approach is investigated and confirmed by comparing modeling results with a layered medium model, a 2D prism model and a 3D model. The bi-conjugate gradient method is applied in solving the governed equations, which reduced the dimensions of the linear system under the first boundary condition.In addition, the memory requirement is reduced obviously in which only nonzero elements stored. The solution of the linear system is obtained by using a massive parallel program based on MPI between frequencies which massively reduced the computing time. A 3D model has been calculated, and the speed-up ratio is up to 2.328 when 4 processes used.

Key words:magnetotelluric; three-dimensional; modeling; parallel programing; MPI