风电齿轮传动系统动力学方程与模态振动特性分析

李　斌　　沈意平　　韩清凯

（湖南科技大学 机械设备健康维护重点实验室，湘潭 411201）

风电齿轮传动系统动力学方程与模态振动特性分析

李斌沈意平韩清凯

（湖南科技大学 机械设备健康维护重点实验室，湘潭 411201）

本文利用相关参数对齿轮传动系统的固有特性与相关激振频率的共振区进行分析。分析表明：系统的低阶固有频率主要表现为与转动频率振动区重叠，系统中的高阶固有频率主要表现为中间轴和高速轴轮系的啮频共振；当系统的固有频率在共振区时，将引起系统的共振，影响系统的正常运行，研究结果将为风电机组齿轮传动系统的设计提供可靠的依据。

风力发电齿轮传动系统动力学模型固有特性

引言

风电齿轮箱通常为含行星轮系的三级斜齿轮传动系统，是具有大传动比、高动载的增速系统。齿轮箱动力学模型包括扭振模型、扭振-平移多自由度模型、柔性多体动力学模型［1-5］，Helsen、何玉林等［6-10］通过理论与实验研究对比并讨论了齿轮箱三种类型模型的准确度和计算效率，指出柔性多体动力学模型能更全面地揭示其耦合振动特性，避免简化数学模型造成频率成分丢失，但模型规模与效率、界面条件是高效准确建模的关键。但这些研究或仅限于对齿轮传动系统的某一部分，或不能完全的反映大型风机齿轮箱系统的振动特性。斜齿轮同时参与啮合的齿对数越多，单对轮齿分担的载荷越少，所以其凭借传动平稳、传递载荷能力强等特点广泛应用。但是，螺旋角过大其轴向力不可忽视，因此斜齿轮动力学系统除具有扭转、横向振动外，还会引起轴向振动，从而形成综合考虑误差激励、时变啮合刚度激励、啮入冲击激励的斜齿轮副啮合型弯-扭-轴耦合振动模型。

本文针对5MW风电齿轮传动系统，对系统弹性变形进行分析，建立平移、扭转六自由度斜齿轮传动系统的动力学分析模型，推导出动力学微分方程；利用该系统的有关参数进行固有特性分析，为齿轮传动系统的动力学响应分析与齿轮箱的设计奠定了基础。

1齿轮传动系统分析模型

图1为风电齿轮传动系统的结构简图，其结构为两级行星轮系+一级平行轴系的传动形式。在图1中，ri表示内齿圈，ci表示行星架，pi表示行星轮，si表示太阳轮（i=1，2）；g1为高速级输入齿轮，g2为高速级输出齿轮；Tin为输入，Tout为输出。表1为齿轮传动系统各个齿轮的参数表。

1.1齿轮传动系统的动力学模型

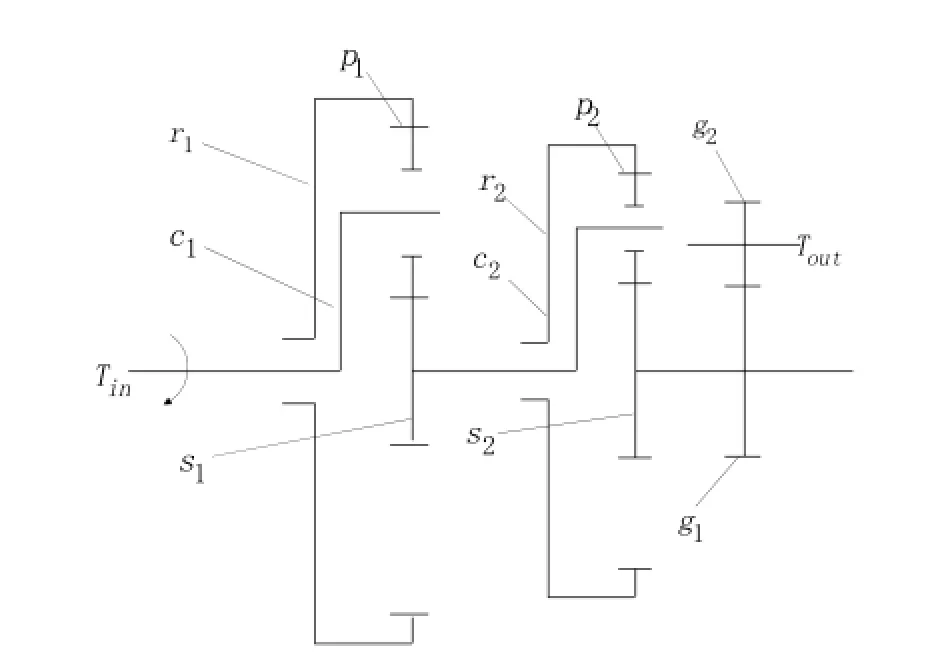
图1风电机组齿轮传动系统结构简图

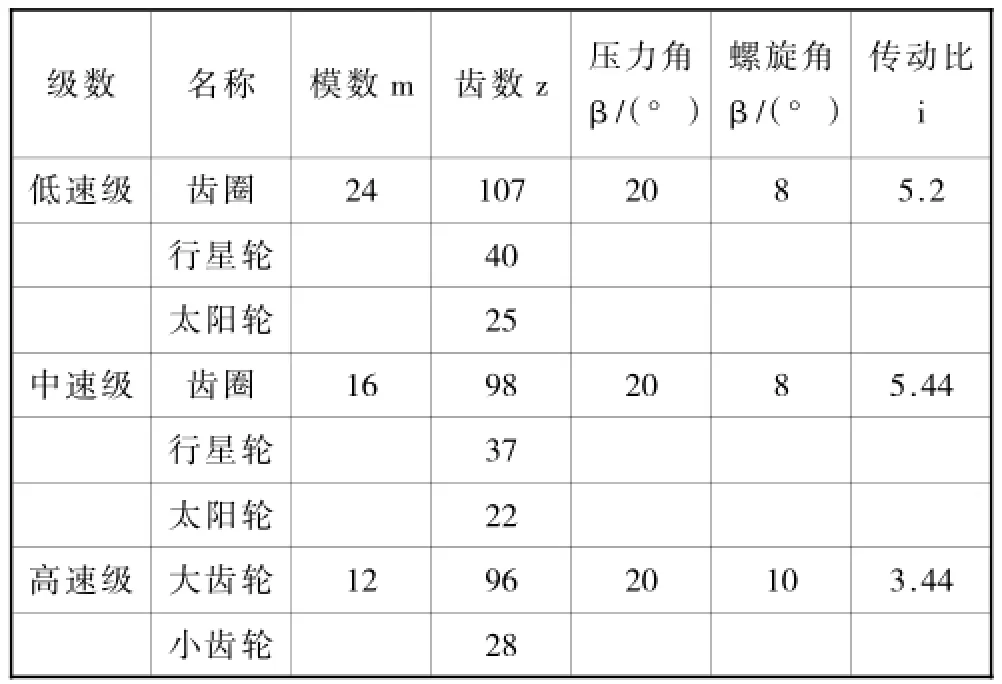
表1齿轮参数表

图2风电齿轮传动系统物理模型

建立系统的动力学模型如图2所示。建立系统模型的关键在于行星传动系统和斜齿轮传动系统，因此，以下内容对行星齿轮传动系统和斜齿轮传动系统的物理模型建模分别进行说明。

图中：kss—连接太阳轮1与太阳轮2轴的扭转刚度；css—连接太阳轮1与太阳轮2轴的阻尼；ks4—连接太阳轮2与斜齿轮 4轴的扭转刚度；cs4—连接太阳轮 2与斜齿轮4轴的阻尼。

内、外啮合齿轮副在大多数行星传动系统中均存在，而且斜齿轮啮合所产生的轴向推力还会影响斜齿行星传动，所以行星轮系传中的动力学特性非常复杂。因此，建立斜齿行星齿轮系统的动力学模型研究其对动力学特性是非常必要的。建立的行星轮系动力学模型主要考虑太阳轮、行星轮的三个平移自由度、三个转动自由度，共有24个自由度。

设x，y，z，θx，θy，θz依次为系统中构件在各自动坐标系内沿三个坐标轴方向的平移位移和绕三个坐标轴的转动位移，以下标区分不同的构件，忽略系杆和内齿圈的质量。设内齿圈下标为r，太阳轮下标为s，行星轮下标为（i=1，2，3，为行星轮的序号）。以r表示齿轮构件的基圆半径，rp表示行星轮基圆半径，rm表示构件节圆半径。

图3行星齿轮传动的动力学模型

太阳轮在啮合面与其端面的交线上、及行星轮在基圆切线方向上的等价线位移采用u表示，则有：

图4平行轴斜齿轮传动动力学模型

（2）平行轴斜齿轮传动动力学模型

图4中，kij为刚度，cij为阻尼，下标j和i分别表示主动轮和从动轮。eij为齿轮i和j啮合副的综合啮合误差；为齿轮i和j啮合副的端面啮合角；

图中，ksx=ksy=ksz，kcnx=kcny=kcnz，ksb=ksu，kcnb=kcnt，其中 ksx，ksy，ksz，knx，knz为行星轮与太阳轮的轴向、径向、周向等效支撑刚度，ksn、kcn为行星轮与太阳轮的啮合刚度，ksb、kcnb为行 星 轮 与 太 阳 轮 的 扭 转 刚 度 ；kix=kiy=kiz（i=4，5），kiθx=kiθy=kiθz（i=4，5），ki为高速级齿轮等效支撑刚度，kiθ为高速级齿轮扭转刚度，阻尼表述与刚度标注一致；Tin为齿轮系统输入扭矩，Tout为齿轮系统输出扭矩，为第二级行星架输入扭矩；ωc为行星轮架转速；ms，mn，m4，m5分别为太阳轮、行星轮、高速级输入齿轮、高速级输出齿轮质量，Is，In，I4，I5分别为太阳轮、行星轮、高速级输入齿轮、高速级输出齿轮转动惯量。

1.2系统各构建的相对位移分析

1）太阳轮与行星轮沿啮合线方向的相对位移

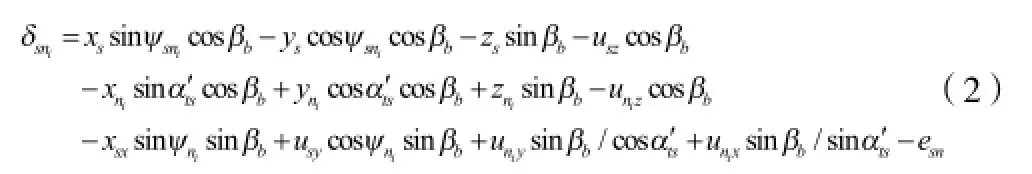
式中，βb为螺旋角；ψni为行星轮ni（i=1，2，3）的位置相角，ψsni=α′ts+ψni（当i=1时，ψni=0；当i=2时，ψni=120°；当i=3时，ψni=240°。）；α′ts为太阳轮和行星轮啮合副的端面啮合角。

2）内齿圈与行星轮沿啮合线方向的相对位移

式中，ern为内齿圈和行星轮啮合副的综合啮合误差；为内齿圈和行星轮啮合副的啮合角。

3）平行轴斜齿轮系的相对位移分析

斜齿轮4与斜齿轮5沿啮合作用线方向的相对位移

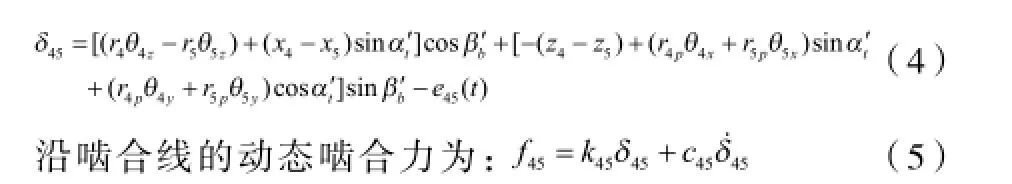
式中：k45、c45—斜齿轮啮合刚度、阻尼；ri、rip（i=4，5）—齿轮基圆、节圆半径；β′b为螺旋角。

1.3系统的动力学微分方程

第一级行星轮系太阳轮：

第一级行星轮系行星轮：

第二级行星轮系太阳轮：

第二级行星轮系行星轮：

高速级斜齿轮4：

高速级齿轮5：

把以上的每个部件的动力学方程组合在一起，就组成了系统的动力学微分方程，简写为：

式中：x为位移向量，它定义为：

θ为齿轮的扭转位移；z为齿轮的轴向位移；x，y为齿轮的径向位移；M、F为系统质量矩阵、外载荷向量；C、K为系统阻尼矩阵、刚度矩阵。

2齿轮传动系统固有特性分析

（1）系统无阻尼自由振动

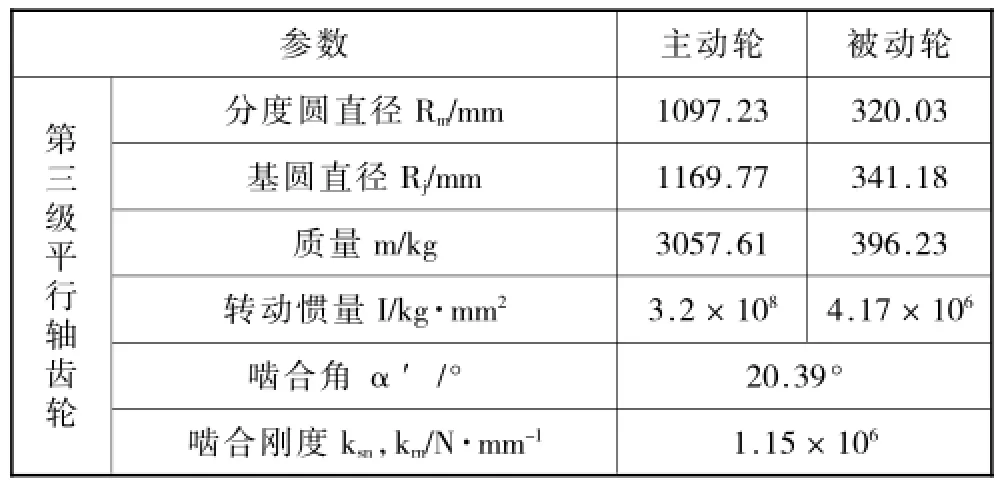
表2平行轴齿轮传动基本参数

表3两级行星轮系传动基本参数

对于n自由度的振动，系统的自由振动微分方程为：

不考虑阻尼和外部载荷的影响时，变为无阻尼自由振动：

设系统的各质量块做相同频率、相同相位做简谐振动，即：

式中：

φ为振幅列阵；ω为圆频率；t为时间变量；φ为初相位。

将式（14）代入系统自由振动微分方程（16）得：

上式两端左乘得：

化简得：

上述方程有非零解的条件为：

方程（20）为系统的特征方程，对其求解可以确定 φ 和ω，振动系统的固有频率和振型的求解在数学上就是求解特征值与特征向量。

（2）齿轮传动系统振动特征频率

转速同步频率：

定轴齿轮啮合频率：

行星轮齿轮中，啮合频率采用下式计算：

式中，n为轴转速（r/min），z为齿轮齿数；ωc为行星轮架转速（r/min），zr为齿圈齿数。

（3）齿轮传动系统模态性结果与分析

工程上规定当固有频率落入激振频率的范围内时容易导致振动，该范围称为共振区［11］。通过分析传动系统的固有频率是否落在工作范围的激振频率共振区内，并通过使固有频率避开激振频率共振区，从而提高其动力学性能，降低振动和动载水平。

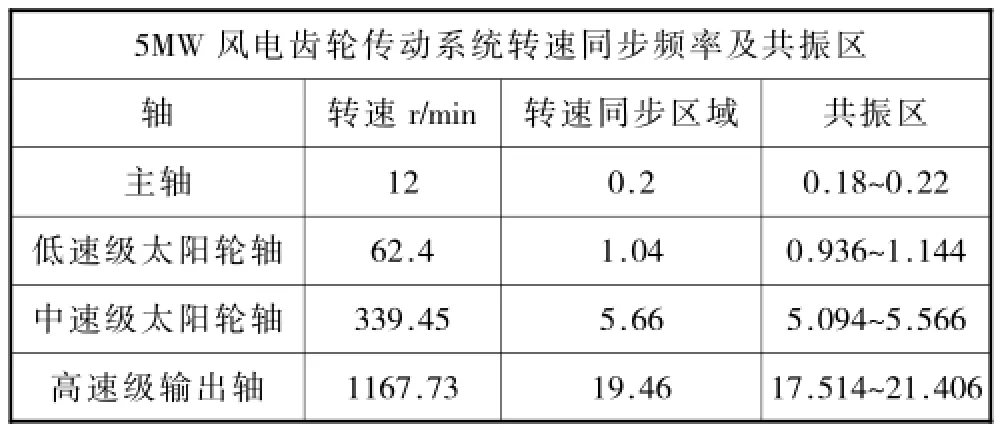
表4齿轮传动系统转速同步频率及共振区

表4列出了所研究对象风电齿轮传动系统各级传动轴的转速、其转速同步频率以及对应的共振区。表5列出了系统的各级齿轮副啮合频率及其对应的共振区。

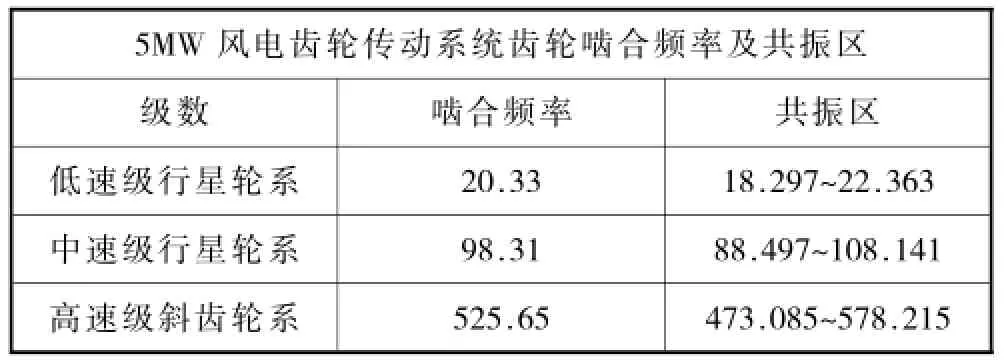
表5齿轮传动系统齿轮啮合频率及共振区

本文取其中的前50阶固有频率，表6列出了5MW风电齿轮传动系统的前50阶固有频率，图5-7给出了部分固有频率的振型图。

因为风力发电机叶轮采用三叶片式，并且每片叶片旋转到底端时都对风机进行一次激励。因此，在风机的设计中就要使系统的低阶固有频率避开风轮旋转频率的1倍频率和3倍频率，即0.2Hz和0.6Hz。

从表4～6的3个图表的计算结果中可以看出：

（1）系统的1阶固有频率在转频共振区避开了风轮1倍转频和3倍转频的激振；系统的1倍转频、3倍转频在啮合频率共振区内并未使系统产生有害的振动；5MW风电齿轮传动系统的50阶固有频率中有2对相等的固有频率，这是因为系统中含有3个行星轮的；第3阶固有频率落入了低速级行星轮系的啮合频率共振区，其振动将会比较剧烈。

表6 5MW风电机组齿轮传动系统前50阶固有频率

图5固有频率f=467.80Hz所对应的振型

图6固有频率f=505.59Hz所对应的振型

图7固有频率f=570.33Hz所对应的振型

（2）第7阶固有频率落入了中速级行星轮系的啮合频率共振区，说明中间级齿轮在设计时要考虑齿轮参数的选取，与啮合频率区重叠产生的振动应尽量避免；第3阶固有频率落入了高速级转频共振区；第31～39阶固有频率落入到了高速级啮合频率共振区。5MW风电机组其高速级齿轮由于固有频率落入了啮合频率共振区的频率阶次较多，振动较大。因此，对于给定的高速级齿轮的啮合频率，在设计时可以开展齿轮的模数、齿宽等设计参数优化，使其固有频率避开啮合频率。

图5高速级平行轴齿轮没有振动，两级行星轮系的行星轮轴均振动，而且两级的行星轮系也都振动且各自的行星轮振动状态相同；图6第一级行星轮轮系的各构件都不振动，第二级行星轮轮系和平行轴齿轮均振动，并且行星轮的振动状态相同；图7第一级行星轮系和第二级行星齿轮的行星轮系均有振动；行星轮系的各级行星轮轴均以不同的幅度作纯扭转振动。

3结论

（1）以两级行星轮系一级平行轴斜齿轮传动系统的5MW风电齿轮传动系统为研究对象，建立了系统的平移与扭转6个自由度的动力学模型；

（2）利用相关参数对齿轮传动系统的固有特性与相关激振频率的共振区进行了分析，系统的低阶固有频率主要表现为与转动频率振动区重叠，系统中的高阶固有频率主要表现为中间轴和高速轴轮系的啮频共振；当系统的固有频率与共振区重叠时，将引起系统的共振；

（3）对于5MW风电机组来说，其高速级齿轮由于固有频率存在啮合频率共振区内的频率阶次较多，导致振动较大。因此在设计时，对于高速级齿轮的啮合频率应加以重视，可以从齿轮的模数、齿宽等设计参数进行修改，从而使其固有频率避开啮合频视率。

［1］Hansen，M.O.L.，Madsen，H.A.Review Paper on Wind Turbine Aerodynamics.Journal of Fluids Engineering，2011，133 （11）：114001-012.

［2］Cordle，A.，Kaufer，D.，Vorpahl，F.，et al.Final report for WP4.3：Enhancement of design methods and standards.Garrad Hassan and Partners Ltd，2011.

［3］Jonkman，J.M.Dynamics modeling and loads analysis of an offshore floating wind turbine.NREL，2007.

［4］Struggl，S.，Berbyuk，V.，Johansson，H.Review on wind turbines with focus on drive train system dynamics.Wind Energy， 2014.

［5］邱星辉，韩勤锴，褚福磊.风力机行星齿轮传动系统动力学研究综述.机械工程学报，2014，50（11）：23-36.

［6］Peeters，J.L.，Vandepitte，D.，Sas，P.Analysis of internal drive train dynamics in a wind turbine.Wind Energy，2006，9（1-2）：141-161.

［7］Helsen，J.，Vanhollebeke，F.，Marrant，B.，et al.Multibody modelling of varying complexity for modal behaviour analysis of wind turbine gearboxes.Renewable Energy，2011，36（11）：3098-3113.

［8］J·rgensen，M.F.，Pedersen，N.L.，S？rensen，J.N.Comparison and implementation of a rigid and a flexible multibody planetary gearbox model.Modeling，Identification and Control，2014，35 （2）：59-77.

［9］LaCava，W.，Xing，Y.，Guo，Y.，et al.Determining wind turbine gearbox model complexity using measurement validation and cost comparison.European Wind Energy Association annual event，2012.

［10］何玉林，黄伟，李成武等.大型风力发电机传动链多柔体动力学建模与仿真分析.机械工程学报，2014，50（01）：61-69.

［11］AdvisoryBoardfortheDanishWindTurbineCertification Scheme.Recommendation to Comply with the Technical Criteria of the Danish Wind Turbine Certification Scheme［S］.The Danish Energy Authority，2005.

Dynamic Equation and Modal Vibration Characteristic Analysis of Wind Power Gear Transmission System

LI Bin，SHEN Yiping，HAN Qingkai
（HunanProvincialKeyLaboratoryofHealthMaintenancefor Mechanical Equipment，Hunan University of Science and Technology，Xiangtan，411201）

The dynamic model of gear system is established by the lumped-parameter method.Analysis was conducted by using the correlationparameterstotheinherentcharacteristicsofthegear transmission system and the resonance region of the relevant excitation frequency.Analysis shows that the low order natural frequency of the system is mainly manifested in the overlap with the rotating frequency vibration area，the high order frequency in the system mainly for meshing frequency resonance intermediate and high speed shaft gear. When the natural frequency of the system is in the resonance zone，willcausedthesystemresonance，affectedthesystem'snormal operation.The results of the study will provide reliable basis for the design of wind turbine gear transmission system.

wind power generation；gear transmission system；dynamics model；natural characteristics

国家自然科学基金资助项目“海上浮式风机整机刚柔耦合多体系统的动力学建模方法的研究”（51205124）。