神经网络模型在水文模拟中的应用研究

王呈会

（辽宁省水文局，辽宁沈阳110003）



神经网络模型在水文模拟中的应用研究

王呈会

（辽宁省水文局，辽宁沈阳110003）

［摘 要］针对传统BP神经网络模型存在收敛精度不高，引入小波函数对传统BP神经网络模型节点计算方法进行改进，并将改进的BP神经网络模型用于大洋河水文模拟研究中。研究结果表明：改进的BP神经网络模型可改变传统神经网络模型的收敛精度，在大洋河流域洪水尺度水文模拟中，相比于传统BP神经网络模型，模拟精度得到明显提高。

［关键词］小波函数；改进BP神经网络模型；水文模拟；模拟精度

1　引言

由于改进的BP神经网络模型在水文模拟研究中应用较少，为此，引入改进的BP神经网络模型，以辽宁东部大洋河流域为例，模拟大洋河流域的水文过程，并和流域内实测水文数据进行对比分析改进的BP神经网络模型在流域水文模拟的精度，研究成果对于区域水文模拟提供参考价值。

2　改进的神经网络模型原理

小波分析函数主要是通过一个基本单一的小波函数构成，经过水平位移和伸缩位移后的所得。然后再与小波分析信号函数进行内部积分，这个积分过程称为小波函数变化过程，该小波变化函数的过程具体表达式为：

在方程（1）中τ表示为小波分析函数中的水平位移量；α表示为小波分析函数中的的横向伸缩量；t表示为计算的时刻。

在小波变换方程中，小波分析函数结合小波信号变换的原理得到分析信号的局部特征值，该局部特征为可以在水平和横向两个方向上进行信号的选择。当前，在小波变化方程中小波变化分析函数主要采用的函数有Shannon小波变化函数、Harr小波变化分析函数、Morlet以及样条分析小波变换函数，各种小波分析函数都具有各自的计算优缺点，在计算过程中主要集合小波信号处理需求进行选择，选择Morlet小波分析函数作为这次小波变化信号处理的小波分析函数。Morlet小波分析函数的主要表现形式为：

改进的BP神经网络模型主要是在传统BP神经网络模型的基础上，引入小波分析函数作为传统BP神经网络模型各个节点计算的控制函数，结合放射变化建立各个节点之间的联系。当模型的输入变量为X=（x1，x2，…，xn），模型的输出变量为Y=（y1，y2…，yn）。集合两个变量（X，Y）可以确定改进的BP神经网络模型各个节点的n，模型隐含的计算节点数l，以及模型的输出变量的自由节点数n，改进的BP神经网络模型的小波分析函数的具体表达式为：

在方程（3）中准（j）表示小波分析函数中隐含的计算节点数j的模型输出值；准j表示的小波分析的基本函数；l表示小波分析函数计算的隐含的计算节点个数。

结合隐含的计算节点数与输出特征层之间的神经系数连接权重值Wjk，小波分析变化函数模型的输出值的表达式为：

在方程（4）中y（k）表示的模型的输出值。

在改进的BP神经网络模型需要采用梯度进行修正通过与实测值之间的相对误差进行反复训练计算，通过调整模型的权重特征值以及小波分析函数的各个参数值，使得改进的BP神经网络模型的输出值和实测值之间的误差减少到许可的范围。模型预测的相对误差计算公式为：

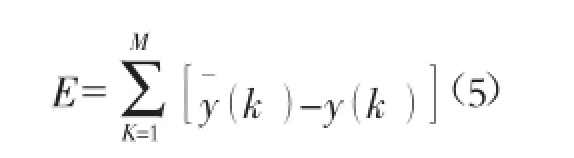
在方程（5）中y軃Σk Σ表示模型训练计算的数值；yΣk Σ表示小波分析函数模型的预测值；m比表示为具体的模型输出的节点的层数。

3　模型运用

3.1研究区域概况

大洋河位于辽宁省东部区域，河流总长为230.2 km，大洋河总的集水面积为6 504 km2，是辽宁省东部半岛区域最大河流，流域的水量较为丰育，水系较多，流域1960—2010年多年平均水量为3.1×109m3，文中的研究区域位于大洋河里寨水文站以上集水区域，研究区域集水面积为4 810 km2，研究区域内有9处雨量站点，流域1960—2010年多年平均降水量为650 mm。

3.2模拟结果对比分析

基于沙里寨水文站1980—2010年水文数据，其中1980—1999年水文数据用于模型训练，计算参数，2000—2010年水文数据用来验证模型模拟精度，模型验证结果见表1。

从表1中可以看出，改进的BP神经网络模型2000—2010年模拟值和沙里寨水文站实测值之间的相对误差均小于10%，而传统的BP神经网络模型2000—2010年模拟值和沙里寨水文站实测值之间的相对误差大都在10%以上，除2010年大水年份外，可见改进的BP神经网络模型在水量模拟误差有所改善，相比于传统BP神经网络模型，改进的BP神经网络模型相对误差均值减少6.57%。其次在水文过程模拟上，改进的BP神经网络模型模拟值和实测值之间的确定性系数均在0.8以上，明显好于传统BP神经网络模型的确定性系数，在确定性系数这一指标上，改进的BP神经网络模型相比于传统的BP神经网络模型，确定性系数提高0.2。可见，改进的BP神经网络模型在年尺度水文模拟上，精度有所提高。

表1改进前后BP神经网络模型模拟结果对比图

4　结论

本文引入改进的BP神经网络模型，并将模型应用于大洋河流域的水文模拟中，研究取得以下结论：

1）改进的BP神经网络模型可提高传统BP神经网络模型收敛精度不高的缺陷，模型收敛速度得到提升。

2）改进的BP神经网络模型适用于大洋河流域的水文模拟，在年尺度上，相比于传统BP神经网络模型，改进的BP神经网络模型年相对误差减少6.57%，确定性系数提高0.2。

［中图分类号］TV124

［文献标识码］B

［文章编号］1002－0624（2016）05－0028－02

[收稿日期]2016-01-20