基于一种新流水步距的工期优化分析*
2016-08-04韬汪梅王艳华李海霞
吴 韬汪 梅王艳华李海霞
(1.安徽新华学院土木与环境工程学院 安徽合肥 230088;2.合肥前城置业有限公司造价部 安徽合肥 230088)
基于一种新流水步距的工期优化分析*
吴 韬1汪 梅2王艳华1李海霞1
(1.安徽新华学院土木与环境工程学院 安徽合肥 230088;2.合肥前城置业有限公司造价部 安徽合肥 230088)
摘 要:传统流水施工组织方法在工程应用中存在工期较长、分层组织时主导施工过程不能连续作业等缺陷。为有效解决上述问题,本文重新界定了流水步距的含义,并引入了逆流水步距概念,从而重新构建了流水工期表达式。该表达式与流水工期的定义形式具有相同的构造组成,可较为方便地更新现有《施工组织》教材中流水施工的相应理论知识点,且实例应用表明,基于新型流水步距的工期优化可以实现工期与资源综合最优的效果,且工期缩短与费用增加可以实现量化评价。
关键词:流水施工 流水步距 工期优化 异步距异节拍
一、问题的提出
流水施工是现代施工管理领域中最科学的施工组织方法之一,并已在各类型的工程建设中得到了广泛应用,工程实践表明,科学合理地应用流水施工原理可以实现资源供应均衡、工期有效缩短、施工质量专业化等综合效益。土木类施工或施工组织的经典教材[1-3]介绍了流水施工的基本原理,如流水施工基本概念、流水参数、流水组织方式等,其中流水步距作为基本流水参数,同时也是间接性参数,在流水组织过程及实现流水工期效益中发挥着重要作用。也一直是流水施工原理的研究热点[4-6]。传统的流水步距有两种定义:其一是指相同施工过程的施工班组先后进入同一个施工段开始施工的最小且合理的时间间隔(不包括间歇和搭接)[3],其二是指相邻施工班组先后入场的最小且合理的时间间隔(不包括间歇和搭接)[1]。第一种定义在应用于成倍节拍流水时,与其流水特性不协调,因为成倍节拍流水的流水步距均相等的这一特性已成为行业共识,而依据第一种定义显然与此特性矛盾,因此第二种定义逐渐被学界和工程界所认同。依据第二种定义,“最小且合理”的含义主要体现出如下特点:(1)施工班组最大限度实现连续作业;(2)相邻施工过程尽可能平行搭接施工;(3)工作面尽可能连续利用。当组织等步距流水(全等节拍流水和成倍节拍流水)时,不分层时以上特点可理想化表现,而分层时则一般需要满足施工段数的限制;当组织异步距流水(异步距异节拍流水和无节奏流水)时,以上特点很难完全体现,不分层时考虑班组连续作业则工期会相对较长,且工作面闲置较长,如图1所示,分层时甚至连“主导施工过程连续作业”的关键流水条件也不能满足[7],如图2所示。工程实践中一般会在图1的基础上进行局部调整,如图3所示,但这种调整缺乏理论依据,调整后的流水工期不能直接应用其定义公式(1)校核评价。式中,,1i iK+为流水步距,NT 为最后一个班组的作业持续时间,1Z为首层层内所有间歇与搭接的代数和。
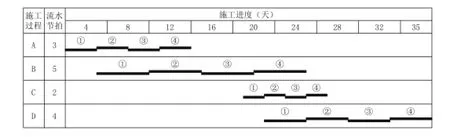
图1 不分层时的流水施工横道图(工期较长)

图2 分层时的流水施工横道图(主导施工过程层间作业不连续)

图3 不分层时的流水施工调整横道图(工期较短)
二、逆流水步距与流水工期优化原理
1.逆流水步距
为解决上述问题,尤其是异步距异节拍流水的施工组织及工期计算问题,本文建议适当调整流水步距定义中“最小且合理”的含义,即将基于班组连续作业的前提改变为基于工作面连续利用,并引入“逆流水步距”参数[7],所谓逆流水步距是指相邻施工班组先后退场的最小且合理的时间间隔(不包括间歇和搭接),用表示,当有N个施工班组时,逆流水步距的数目为(N-1)。
于是,流水步距和逆流水步距可分别按照式(2)和式(3)计算,如图4所示,能满足关键条件“主导施工过程连续作业”的约束。
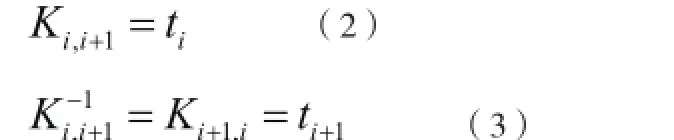
式中,it为第i个施工过程的流水节拍,1it+为第i+1个施工过程的流水节拍。
2.流水工期优化原理
重新界定流水步距含义及引入逆流水步距后的横道图如图4所示,比较图3和图4可知,两者工期相同,而图3可理解为在基于工作面连续利用的前提下实现最大程度的班组连续作业和施工过程最大限度的平行搭接。因此流水工期可参照图4,并依据定义公式(1)的概念化结构建立其表达式(4),进一步地,代入式(2)、(3)后,式(4)可简化成式(5)。
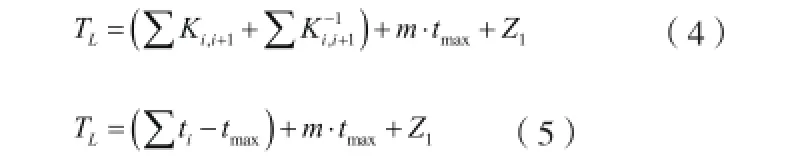
式中,m为施工段数,maxt为主导施工过程的流水节拍,其他符号与前文同。
于是,在资源总量不变的情况下,合理最短的工期可根据式(5)直接确定,而最优进度横道图可参照“图4→图3”的优化思路分两步绘制。
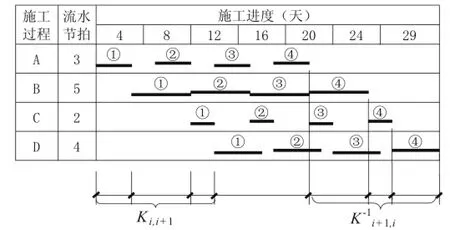
图4 流水步距与逆流水步距
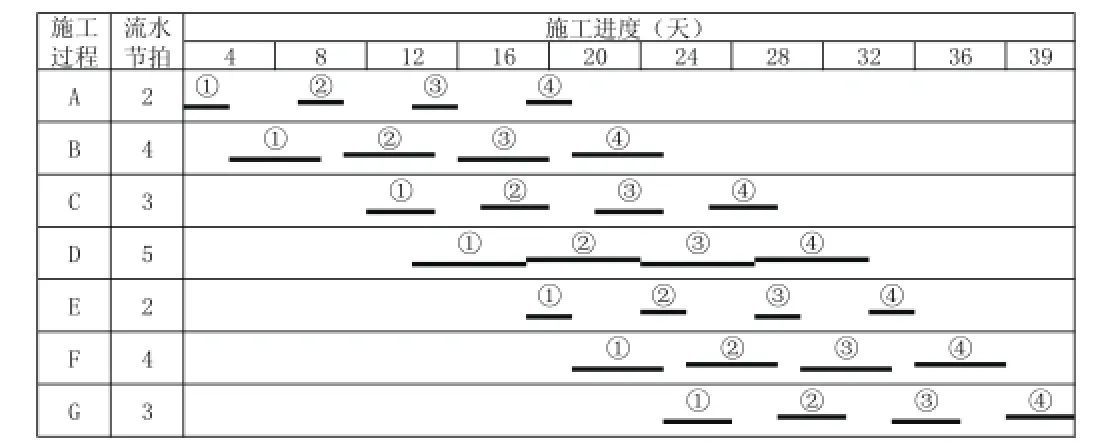
图5 基于工期最优原则绘制的横道图

图6 基于工期和资源综合最优原则绘制的横道图
三、应用分析
某工程按照异步距异节拍流水组织施工,包括施工过程A、B、C、D、E、F、G,含4个施工段,不分层,各施工过程的流水节拍分别为2、4、3、5、2、4、3,B、C之间存在2天技术间歇,C、D之间存在1天组织搭接。
依据式(5)计算流水工期为39天,而依据式(1)计算的流水工期为48天,可见应用本文的优化方法工期缩短了9天,降幅达18.75%。
基于工作面连续的新流水步距及其他流水参数,绘制横道图(即工期最优原则)如图5所示,再按照图3的传统思路尽量压缩班组作业的不连续时间,优化后的横道图(即工期和资源综合最优原则)如图6所示。
图6反映了C、D之间组织搭接参数的目的是为了组织D班组提前入场施作第一个施工段,以缩短工期,此后施工段可不考虑搭接关系;且图6中班组作业不连续的总时间为9天,正好等于按式(5)和式(1)计算的工期缩短差值,由此也可以获得进一步的结论,即在不考虑间歇和搭接的前提下,依据(5)计算得到的最优工期减少值即为班组作业不连续时间,这一结论不仅是初始横道图优化的目标,还可作为工期缩短与成本增加综合效益分析的评价指标。
四、结论
本文在不改变流水参数具体数值的前提下,基于最优流水工期为目标,重新界定了流水步距的含义,并引入了逆流水步距,进而建立了流水工期新的简明计算表达式,结合不分层时的异步距异节拍流水施工组织实例表明,本文提出的新型流水步距可以实现最短工期及其量化的优化目标,不仅完善了现有传统教材中关于流水施工的理论知识,而且在实例中采用的施工组织方法与思路可以直接应用于工程实践。
参考文献:
[1]重庆大学,同济大学,哈尔滨工业大学.土木工程施工[M],北京:中国建筑工业出版社,2008.
[2]于立君,孙宝庆.建筑工程施工组织[M],北京:高等教育出版社,2014.
[3]危道军.建筑施工组织[M],北京:中国建筑工业出版社,2013.
[4]鲁雷,崔秀琴.流水步距定义问题的分析[J],焦作大学学报,2007,(1):92-93.
[5]何夕平.搭接与间歇对流水施工工期影响分析[J],四川建筑科学研究,2004,30(2):107-108.
[6]续宪宏,向健.关于流水步距和流水工期计算方法的讨论[J],甘肃科技,2007,23(6):155-156,66.
[7]吴韬,张文振,张劼,等.基于逆流水步距组织分层无节奏流水施工[J].合肥学院学报(自然科学版),2014,24(1):92-96.
本文创新点:
1.重新界定了流水步距的含义
2.引入逆流水步距参数,并提出其计算方法
3.基于新的流水步距和逆流水步距,构建了最优流水工期的计算表达式
4.提出基于工期和资源综合优化的流水施工组织方法
作者简介:
吴韬(1982-),男,安徽东至人,安徽新华学院土木与环境工程学院讲师,硕士,研究方向:工程结构动力分析与防震减灾。
*基金项目:安徽省教育厅教研项目(2012jyxm584);安徽新华学院教研项目(2013jy036);安徽新华学院骨干教师资助项目(2012xgg03)。
