浅析几类奇异积分算子的有界性

薛庆平 赵 辉

（河南牧业经济学院 河南郑州 450000）

浅析几类奇异积分算子的有界性

薛庆平 赵 辉

（河南牧业经济学院 河南郑州 450000）

对具有非光滑多线性奇异积分算子有界性进行研究。对一类广义Morrey空间次线性算子有界性进行探讨；深入阐述了非其次空间中Marcinkiewicz积分交换算子的有界性。

奇异积分算子 Morrey空间 Marcinkiewicz积分 有界性

引言

为了对非光滑核的多线性奇异积分算子进行研究，首先对极大交换子Cotlar不等式进行构建，通过非光滑核多线性奇异积分算子加权有界性，对非光滑核多线性奇异积分算子有界性进行证明。[1]

一、一类广义Morrey空间次线性算子有界性

Morrey为了对二阶椭圆偏微分方程解局部渐进行为进行研究，第一次引进经典Morrey空间。对于偏微分方程解正则性中，Morrey空间的研究具有非常重要的意义。下文就一类广义Morrey空间次线性算子有界性的进行探讨。[2]

式中， C0≥1，是绝对常数；假设Ω作为零次齐次函数，同时，有。当α , p ,q,r满足任何一个下面的条件：

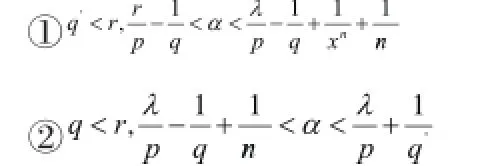
对于固定球 B= B(x0,d)，存在

将上式进行分解，

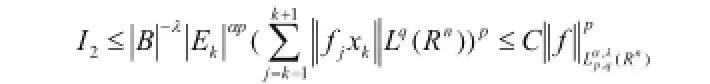
就I1，如果，那么，因此，

从而，证明了一类广义Morrey空间次线性算子的有界性。

二、非齐次空间中Marcinkiewicz积分交换算子的有界性

问题提出，假定μ是在 Rd上的正Radon测度，同时，与以下的增长条件吻合，就全部，存在式中，为正数，同时，满足 0＜n≤d,B(x,r)表示的是x是一个半径r的开球。就任何的，当，那么就叫μ是倍测度。

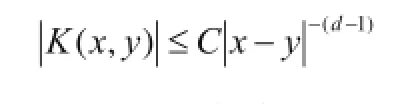
从而进行核 ),(yxK 的Marcinkiewicz积分算子的定义：

同理可得，

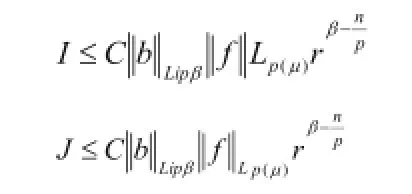
从而证明了非其次空间中Marcinkiewicz积分交换算子的有界性。

三、结束语

通过对一类广义Morrey空间次线性算子有界性和非其次空间中Marcinkiewicz积分交换算子的有界性的研究，针对不同函数空间中算子有界性的研究，为积分算子的有界性研究提供了参考。

[1]陈晓丽，陈杰诚.次线性算子在一类广义Morrey空间上的有界性及其应用[C].数学年刊A辑.2011.32:705-720

[2]陈秀琼.新型各向异性奇异积分算子的有界性[J].汕头大学学报（自然科学版）.2014.11（15）：26-30

[3]叶晓峰，胡媛媛.非其次空间上几类积分算子的有界性[J].华东交通大学学报.2012.8（15）：68-72