构配件构造因素对悬挑脚手架稳定承载力的影响*
2016-08-04李宝平穆召龙曾凡奎
李宝平,穆召龙,蔡 斌,曾凡奎
(西安工业大学 建筑工程学院,西安 710021)
构配件构造因素对悬挑脚手架稳定承载力的影响*
李宝平,穆召龙,蔡斌,曾凡奎
(西安工业大学 建筑工程学院,西安 710021)
摘要:为确定构配件不同构造因素下悬挑脚手架的稳定承载力,利用ANSYS有限元软件对扣件式钢管脚手架稳定承载力的影响因素以及不同构造因素下悬挑脚手架的屈曲变形进行了数值模拟分析.分析结果表明:脚手架稳定承载力受剪刀撑斜杆与大横杆夹角的变化影响显著,立杆间斜撑的设置方式对脚手架承载力有明显影响;增加斜撑长度,不同步距下脚手架承载力随之逐步下降,单位连墙件承载面积越小,脚手架的整体稳定性越好,稳定承载力越大.
关键词:悬挑脚手架;构造因素;屈曲变形;稳定承载力
随着高层建筑施工脚手架技术的发展,脚手架的搭设高度越来越高,导致了脚手架受荷不稳定的可能性,施工中各种不确定荷载的变化也使得脚手架受力复杂,这种状况极易导致脚手架因局部受荷过大而失稳,为建筑施工安全埋下重大的安全隐患.目前对悬手架体系的研究并不完善,导致设计人员在设计施工时缺乏理论依据,且绝大多数的工人对该体系存在认识上的偏差,在施工设计时采取半经验半概率的方式,存在较大的安全隐患,进而频频发生脚手架事故[1-2].扣件式钢管脚手架安装灵活方便,在各种建筑结构形式中通用性强,具有良好的经济效益,在土建施工过程中大量使用,相较常用的其他类型脚手架应用范围最为广泛,在施工单位对脚手架的选择使用中占据绝对的优势.随着各种建筑新材料的发展应用,许多新型脚手架也逐步进入到建筑工程施工的各个过程[3-4].
对于扣件式钢管脚手架的工作性能的研究显得尤为重要,国内外专家学者对此开展了大量研究.文献[5]对双排扣件式钢管脚手架工作性能进行了理论分析和试验研究,通过实验得到了保证脚手架结构刚度的扣件扭矩值的最低值,并与规范进行了对照分析,试验结果与规范规定的最低值相吻合.文献[6]给出了排架计算模型,认为与扣件式钢管脚手架的工作性能更加符合,但前提条件是扣件的拧紧力矩不足以承受脚手架正常工作,文献以该模型为基础,以试验结果和理论计算相结合的方式,进行了脚手架临界力的计算,计算结果表明,排架模型下的脚手架临界力计算方法可以很好地解决工程中脚手架搭设高度的问题.文献[7]采用格构式模型进行了脚手架稳定承载力的理论分析,并通过实际算例提出了针对脚手架稳定承载力的一种具有通用代表性的计算方法,推导过程中对影响其稳定承载力的各种因素(包括连接节点的半刚性)进行了考虑.通过原型试验结果和理论分析结果的对比,验证了该通用计算方法的可行性.文献[8]认为节点连接刚度对脚手架的屈曲承载力具有重要的影响,通过对非线性分析中考虑二阶效应的脚手架分析方法进行论述,提出采用弹性屈曲的方法分析脚手架的屈曲承载力,在分析脚手架杆件的有效长度时应该考虑连接节点的刚度.文献[9]以4种不同类型的大约5 m高的框架脚手架结构的载荷试验为基础,结合ANSYS有限元软件对试验中的脚手架模型进行了非线性屈曲分析,分别得到4种不同类型脚手架的特征屈曲值,通过与试验得到的脚手架极限承载力的对比,发现有限元结果和试验结果相接近.文献[10]对以色列最近出版的模板规范进行了研究,该规范在研究美国、欧洲以及澳大利亚的规范和一些类似的文件后,提出了一些比较新颖的观点:以永久结构的设计方法设计临时结构,通过比较得到了可能影响建筑安全和经济性的设计荷载数据.本文利用ANSYS有限元软件对扣件式钢管脚手架稳定承载力的影响因素以及不同构造因素下悬挑脚手架的屈曲变形进行了数值模拟分析,以确定悬挑脚手架稳定承载力,为脚手架设计及施工搭设提供可靠依据.
1有限元模型的建立
在ANSYS中选取梁单元BEAM188单元如图1所示.BEAM188单元是基于Timoshenko梁理论,具有扭切变形效果,其为一个二节点的三维线性梁.BEAM188单元在每个节点上有6或7个自由度,其数目的变化是由分析参量KEYOPT(1)来控制的.当KEYOPT(1)=0时(默认),每节点有6个自由度.分别是沿X,Y和Z方向的位移及绕其的转动.当KEYOPT(1)=1时,会添加第七个自由度(翘曲量).此元素能很好地应用于线性分析,以及大偏转、大应力的非线性分析.I,J和K为BEAM188单元的节点.
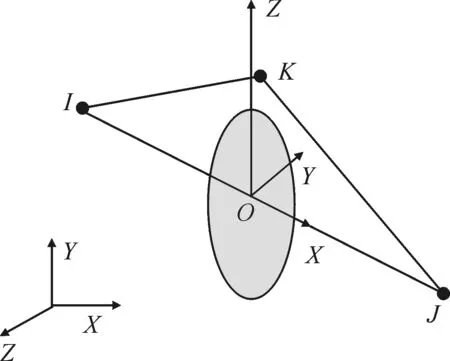
图1 BEAM188单元几何特性Fig.1 Geometric properties of BEAM188 unit
在默认情况下假设BEAM188元素横截面上的弯曲很小,可以被忽略(KEYOPT(1)=0).也可以使用KEYOPT(1)=1来打开弯曲度的自由度.若此自由度被打开,每个节点会有7个自由度:UX,UY,UZ,ROTX,ROTY,ROTZ和WARP.BEAM188单元允许用一个轴向延伸率的函数来改变横截面的转动惯量.默认情况下元素横截面的面积可以改变,但元素的体积在变形前后是相同的.此默认同样适用于弹塑性情况,使用分析变量KEYOPT(2),能使横截面面积为一个常量或保持不变.
在建模过程中,采取由下到上的顺序,关键点-线-面-体,再对体进行划分,划分成单元.单元的属性参考BEAM188单元的性质进行设置.采用子空间迭代法进行静力分析,对模态进行扩展,得到整个架体的屈曲荷载,提取出静力变形图;按照大变形理论进行非线性屈曲分析,得到屈曲荷载和非线性变形图.设定脚手架立杆间距为1.05 m,跨距为1.5 m,步距为1.8 m,可得到经典脚手架模型,如图2所示.
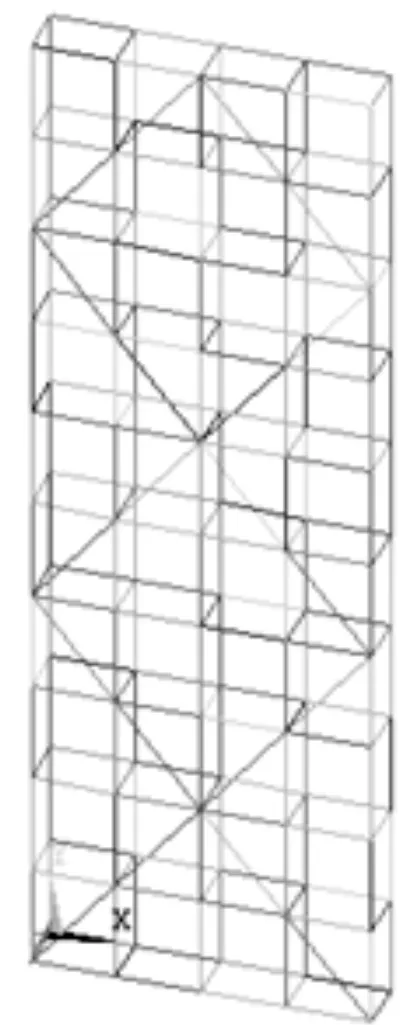
图2 经典脚手架模型Fig.2 Classical scaffolding model
2脚手架构配件布置对承载力的影响分析
扣件式钢管脚手架体系在受到的荷载超过其极限承载力时会表现出失稳模态,根据实际工程案例,脚手架架体失稳主要表现为整体失稳和局部失稳,其中整体失稳更难预防,造成的危害更加不可预计,是架体失稳的主要形式.扣件式钢管脚手架体系整体呈现出高且窄的形态,其横向框架是由双排立杆和双排大横杆共同构成,因而脚手架整体横向刚度较低,在架体整体失稳时会产生纵向与建筑物主体结构垂直的大波鼓曲现象,且鼓曲波长大于脚手架相邻立杆间距.架体局部失稳相对于整体失稳产生的鼓曲较小,且鼓曲发生在上下大横杆之间的立杆上,鼓曲波长与脚手架相邻立杆间距较接近.在其他条件不变的情况下,脚手架稳定承载力主要受构件材质、步距、连墙件布置密度、剪刀撑及横向剪刀撑等因素影响,材质的各种初始缺陷(管材壁厚锈蚀变薄,循环使用弯曲等)对脚手架承载力的影响具有不确定性,存在安全隐患;步距的不同能够明显影响立杆上下两个扣件间的计算长度,进而影响杆件受压稳定性;剪刀撑通过连接立杆和大横杆,在整体上起着协调架体的作用,保证了架体的整体刚度和稳定性,能够在一定程度上提升脚手架稳定承载力;连墙件的布置可以抵抗水平荷载,传递拉力和压力,对于加强脚手架的整体稳定性和避免出现坍塌等事故具有重要的作用;横向斜撑杆的设置可以增加横向框架的整体刚度,使其在失稳时具有足够的抗侧移能力,提高脚手架整体极限承载能力[11-13].
2.1竖向剪刀撑对脚手架体系稳定承载力的影响分析
通过对脚手架设置外立杆剪刀撑、内立杆剪刀撑、内外立杆剪刀撑及外立杆剪刀撑,交叉不同角度时脚手架的屈曲承载能力来确定竖向剪刀撑对脚手架稳定性的影响.当设置外立杆剪刀撑时,屈曲变形如图3所示,在第一荷载步作用下脚手架明显发生向Z轴方向的屈曲变形,单根立杆荷载达到最大值11.49 kN时脚手架整体发生变形,最大变形发生在脚手架的顶端角部,最大位移方向为Z轴方向.当设置内外立杆剪刀撑时,屈曲变形如图4所示,在第一荷载步作用下脚手架明显发生向Z轴方向的屈曲变形,单根立杆荷载达到最大值26.97 kN 时脚手架整体发生变形,最大变形也发生在脚手架的顶端角部,最大位移方向为Z轴方向.对比两种剪刀撑的设置方式可知,当脚手架设置内外立杆剪刀撑时,脚手架的承载能力有一定提高.

图3 竖向外立杆剪刀撑下屈曲变形图(mm)Fig.3 Buckling diagram under outside pole scissors (mm)
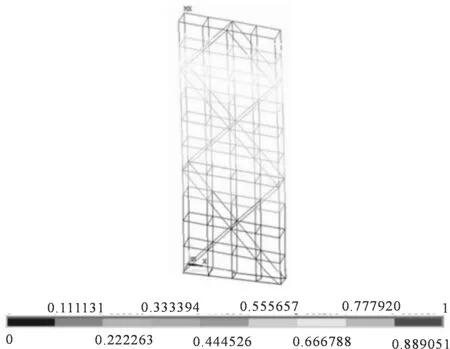
图4 竖向内外立杆剪刀撑下屈曲变形图(mm)Fig.4 Buckling diagram under inside-out pole scissors (mm)
当仅设置外立杆剪刀撑,剪刀撑与地面夹角成60° 时,屈曲变形如图5所示,在第一荷载步作用下脚手架发生向Z轴方向的屈曲变形,在单根立杆荷载达到最大值8.64 kN时脚手架整体发生变形,最大变形发生在脚手架的顶端中部,最大位移方向为Z轴方向,相较于剪刀撑与地面夹角为45°时(如图3所示),脚手架的单杆承载能力下降了24.6%.结果表明,脚手架剪刀撑夹角发生变化时,脚手架的稳定承载能力受到影响,因此,剪刀撑的合理布置能够改善脚手架的承载能力.
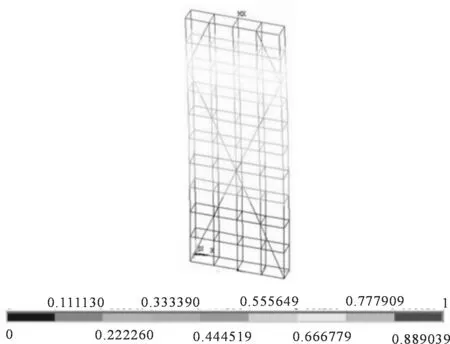
图5 剪刀撑与地面夹角60° 下屈曲变形图(mm)Fig.5 Buckling diagram under scissors with angle of 60° to ground (mm)
2.2连墙件密度对脚手架稳定承载力的影响分析
通过对脚手架设置內立杆和建筑墙体,或梁板柱间设置连墙件的疏密来确定连墙件对脚手架整体稳定承载能力大小的影响,当连墙件两步两跨布置时,屈曲变形如图6所示.
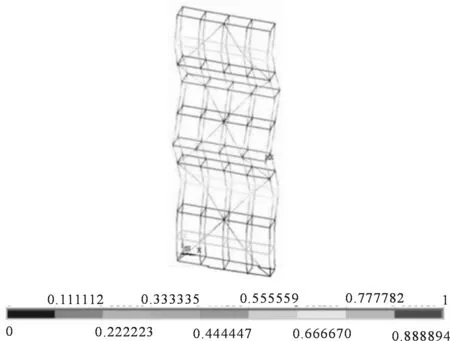
图6 连墙件两步两跨布置下屈曲变形图(mm)Fig.6 Buckling diagram under wall pieces with two-step and two-cross (mm)
在第一荷载步作用下脚手架明显发生向Z轴方向的屈曲变形,在单根立杆荷载达到最大值20.32 kN时脚手架整体发生变形,最大变形发生在未布置连墙件的外立杆上,即是在脚手架上下连墙件的中间位置,脚手架发生明显鼓曲变形,最大位移方向为Z轴方向.
当连墙件三步四跨布置时,屈曲变形如图7所示,在第一荷载步作用下脚手架上部明显发生向Z轴方向的屈曲变形,在单根立杆荷载达到最大值15.15 kN时脚手架整体发生变形,最大变形发生在脚手架顶部,脚手架发生明显鼓曲变形,脚手架顶部位置明显朝向Z轴正方向位移.由于连墙件布置密度变小,脚手架稳定承载能力相较于两步两跨布置时下降了25.4%.
当连墙件四步四跨布置时,屈曲变形如图8所示,在第一荷载步作用下脚手架上部明显发生向Z轴方向的屈曲变形,在单根立杆荷载达到最大值12.41 kN时脚手架整体发生变形失稳,最大变形发生在脚手架顶部,脚手架发生明显弯曲变形,脚手架顶部位置明显朝向Z轴正方向位移.

图7 连墙件三步四跨布置下屈曲变形图(mm)Fig.7 Buckling diagram under wall pieces with three-step and four-cross (mm)

图8连墙件四步四跨布置下屈曲变形图(mm)
Fig.8Buckling diagram under wall pieces with four-step and four-cross (mm)
随着连墙件布置密度减小,脚手架稳定承载能力相较于三步四跨下降了38.9%,相较于两步两跨下降了18.1%.
当连墙件分别按照两步两跨、三步四跨和四步四跨布置时,单个连墙件在设定模型上所负载的面积分别为10.8 m2, 32.4 m2和43.2 m2.结果表明,随着连墙件布置密度的减小,脚手架的稳定承载能力明显下降,即单个连墙件的负荷面积越大,脚手架的稳定承载能力越小.
2.3水平剪刀撑对脚手架稳定承载力的影响分析
设定剪刀撑为外立杆四步四跨布置,连墙件两步两跨布置时的模型为经典脚手架模型,分析水平剪刀撑的布置方式对脚手架稳定承载力时,采取改变其步数和跨数的方式进行研究.当采用上述经典脚手架模型,水平剪刀撑分别按照两步两跨和四步四跨布置时,屈曲变形分别如图9~10所示.
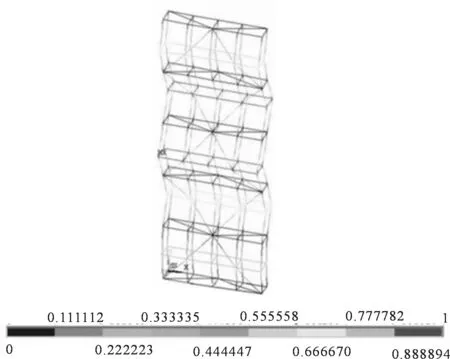
图9 水平剪刀撑两步两跨布置下屈曲变形图(mm)Fig.9 Buckling diagram under horizontal scissors with two-step and two-cross (mm)
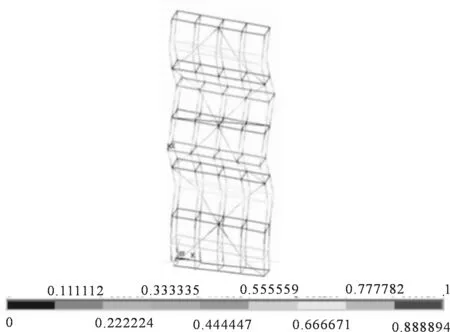
图10 水平剪刀撑四步四跨布置下屈曲变形图(mm)Fig.10 Buckling diagram under horizontal scissors with four-step and four-cross (mm)
根据图9~10分析可知,水平剪刀撑两步两跨和四步四跨布置情况下,脚手架的第一荷载步屈曲承载能力分别为20.4 kN和20.3 kN,脚手架在没有布置连墙件的位置均发生明显的屈曲变形,变形方向均为Z轴方向.当不布置水平剪刀撑时,屈曲承载能力为20.32 kN时脚手架发生屈曲失稳,水平剪刀撑四步四跨布置时脚手架的屈曲承载能力相较于两步两跨仅下降了5.0×10-3%,水平剪刀撑不布置时脚手架承载能力相较于两步两跨下降了3.9×10-3%,即水平剪刀撑的布置与否、水平剪刀撑的跨度以及步高的变化对脚手架的承载能力没有显著影响.
2.4立杆间斜撑对脚手架稳定承载力的影响分析
设定剪刀撑为外立杆四步四跨布置,连墙件为两步两跨布置,不布置水平剪刀撑的脚手架模型为基本模型,通过对脚手架立杆间设置斜撑,并根据立杆间斜撑步高和跨步的变化,来确定立杆间斜撑对脚手架整体稳定承载力的影响.
当采用上述经典脚手架模型,竖向斜撑按两步两跨布置时,屈曲变形如图11~12所示.脚手架第一荷载步屈曲承载力为24.9 kN,在没有布置连墙件的位置发生明显的屈曲变形,变形方向为Z轴方向.
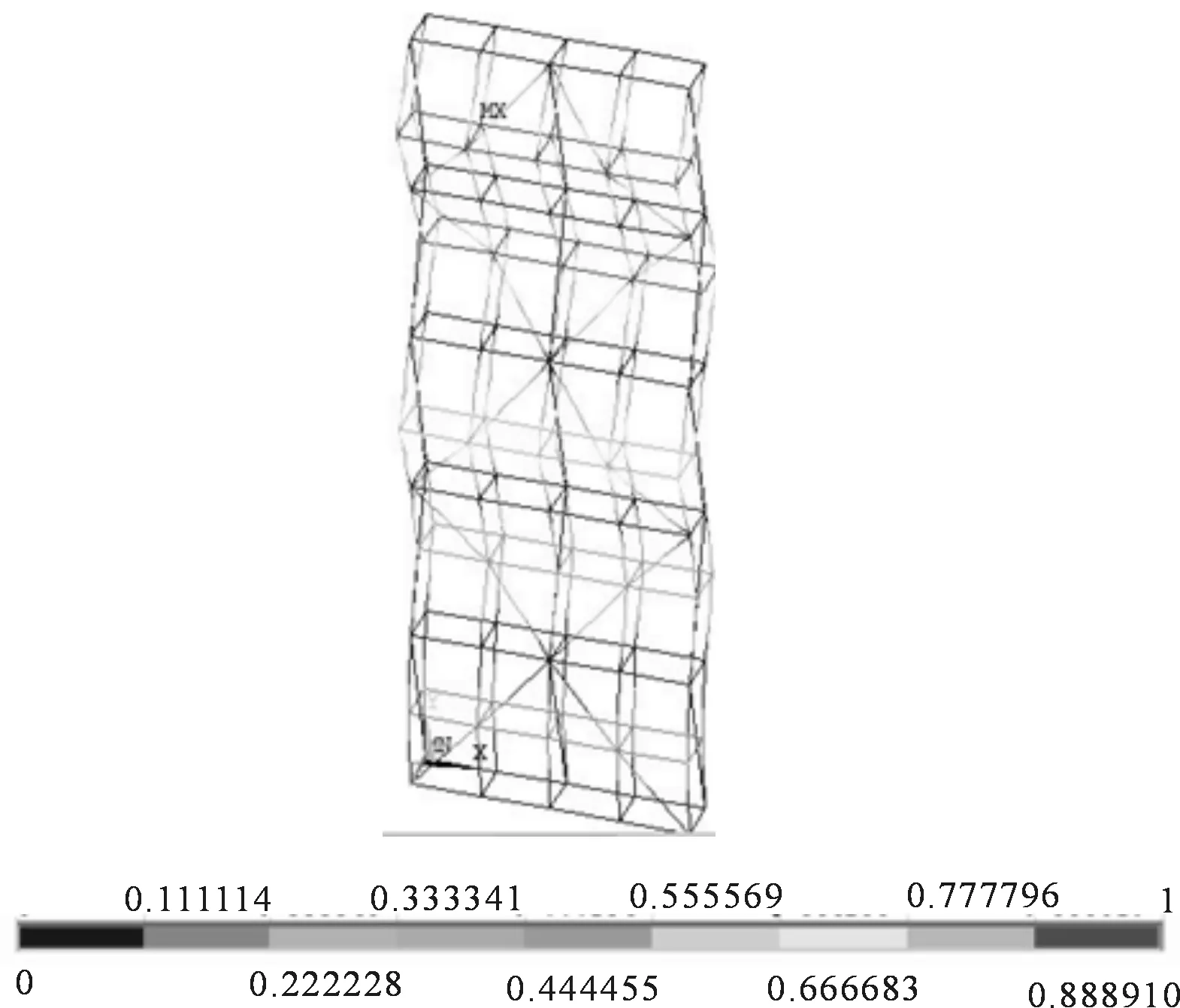
图11 立杆间斜撑两步两跨布置下屈曲变形图(mm)Fig.11 Buckling diagram under diagonal brace with two-step and two-cross (mm)
当采用上述经典脚手架模型,竖向斜撑按照一步两跨布置时,屈曲变形如图13~14所示,脚手架的第一荷载步屈曲承载能力为48.5 kN,脚手架在顶端两步内的位置发生明显的屈曲变形,而脚手架除顶端两步内有明显变形外,其他部分均没有明显的屈曲变形.
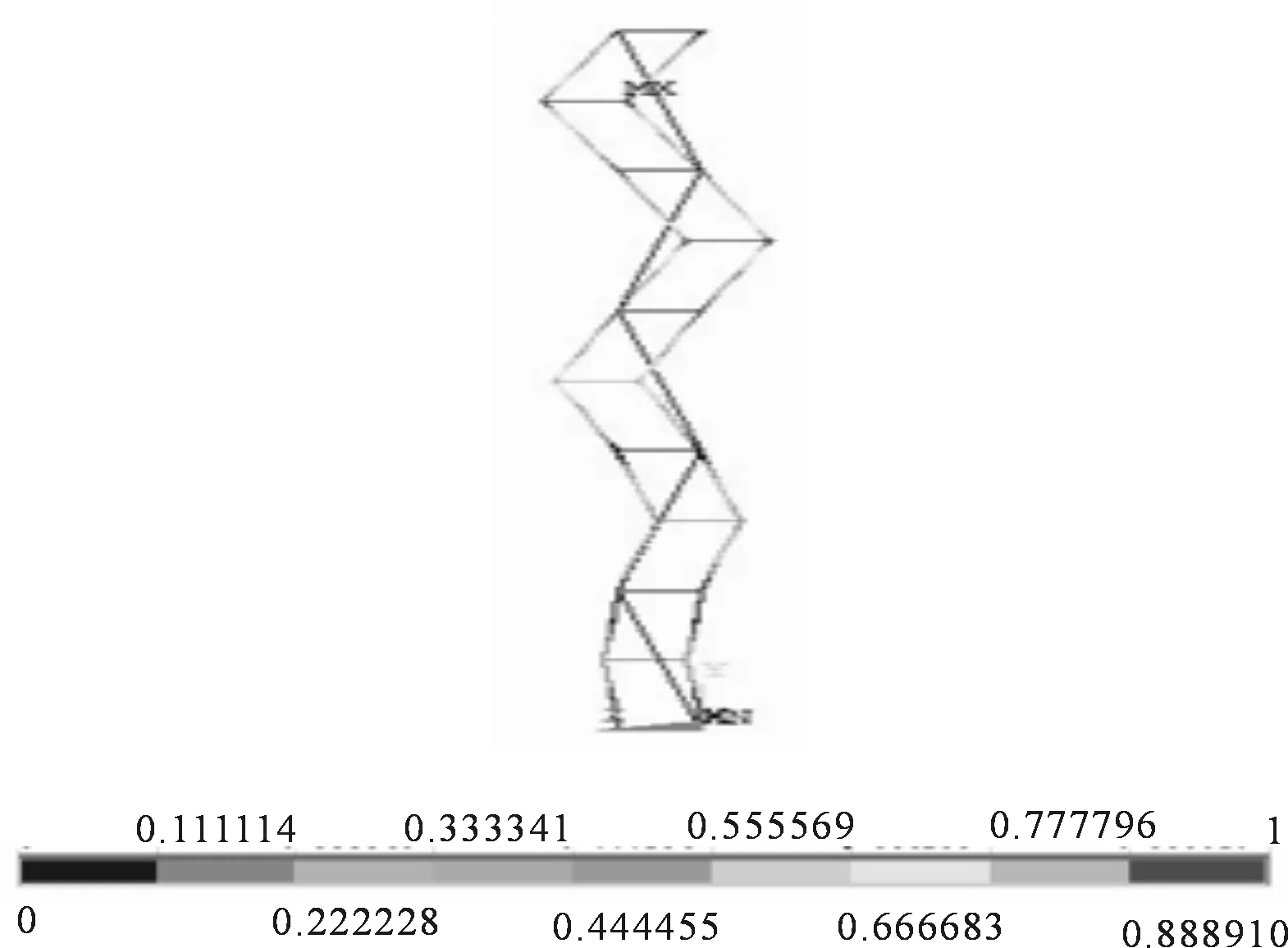
图12 立杆间斜撑两步两跨布置Z轴变形图(mm)Fig.12 Z-axis deformation diagram under diagonal brace with two-step and two-cross (mm)

图13 立杆间斜撑一步两跨布置下屈曲变形图(mm)Fig.13 Buckling diagram under diagonal brace with one-step and two-cross (mm)
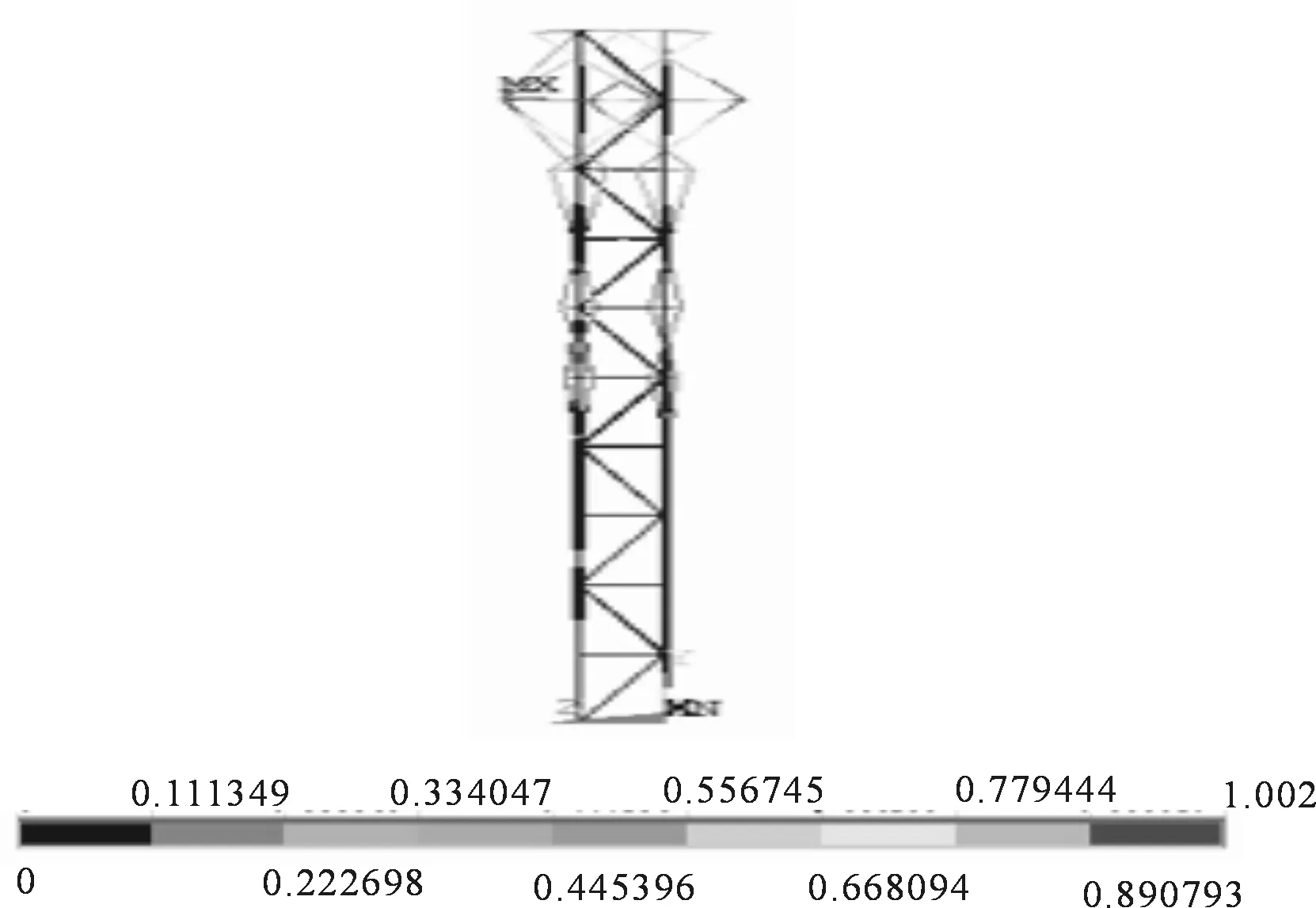
图14 立杆间斜撑一步两跨布置Z轴变形图(mm)Fig.14 Z-axis deformation diagram under diagonal brace with one-step and two-cross (mm)
对比两种立杆间斜撑布置情况可知,立杆间斜撑为两步两跨布置时,脚手架的承载能力相较于一步两跨布置时提高了94.8%.若不布置立杆间斜撑,脚手架的承载能力为20.32 kN,相较于一步两跨布置时,减小了41.9%.故在同等条件下,立杆间斜撑的布置能大幅提升脚手架的承载能力.
3结 论
1) 设置剪刀撑显著提高了脚手架的承载力.在设置竖向内外立杆剪刀撑时,脚手架的承载能力大于仅设置外立杆剪刀撑的情况,且剪刀撑与水平地面夹角的大小对脚手架的承载力有显著影响,设置水平剪刀撑对脚手架承载能力没有影响.合理布设剪刀撑实现了脚手架稳定承载力的提升.
2) 当设置连墙件时,脚手架承载性能明显优于未设置连墙件的脚手架;连墙件密度越大,脚手架承载力也越大,即单个连墙件的负荷面积越小,脚手架的稳定承载能力越大.
3) 设置立杆间斜撑实现了脚手架稳定承载性能的提升,且斜撑设置步高对脚手架稳定承载性能影响显著.
参 考 文 献:
[1]杜荣军.建筑施工脚手架实用手册[M].北京:中国建筑工业出版社,1994.
DU Rongjun.Practical Manual of Construction Scaffolding[M].Beijing:China Architecture and Building Press,1994.(in Chinese)
[2]葛召深,胡长明,王静,等.扣件式钢管模板支架剪刀撑研究[J].中国建筑金属结构,2009(5):62.
GE Zhaoshen,HU Changming,WANG Jing,et al.Study on Bridging of Fastener-style Steel Pipe Formwork Support[J].Construction Technology,2009(5):62.
(in Chinese)
[3]陆征然,陈志华,王小盾,等.扣件式钢管满堂支撑体系稳定性的有限元分析及试验研究[J].土木工程学报,2012(1):49.
LU Zhengran,CHEN Zhihua,WANG Xiaodun,et al.Experimental and Finite Element Study of the Bearing Capacity of Fastener Steel Tube Full-hall Formwork Support System[J].China Civil Engineering Journal,2012(1):49.(in Chinese)
[4]陈培润,杨晓华.对悬挑脚手架一次悬挑高度的探讨[J].建筑安全,2009,24(2):13.
CHEN Peirun,YANG Xiaohua.The Study for A High Degree of Cantilever Scaffold[J].Construction Safety,2009,24(2):13.(in Chinese)
[5]徐崇宝,张铁铮,潘景龙,等.双排扣件式钢管脚手架工作性能的理论分析与实验研究[J].哈尔滨建筑大学学报,1989,22(2):38.
XU Chongbao,ZHANG Tiezheng,PAN Jinglong,et al.Theoretical Analyses and Experimental Study on Working Behavior of Tubular Steel Scaffold Joining by Couplers[J].Journal of Harbin University of Construction,1989,22(2):38.(in Chinese)
[6]刘宗仁,涂新华,丁永胜.扣件式钢管脚手架临界力下限计算方法[J].建筑技术,2001,32(8):541.
LIU Zongren,TU Xinhua,DING Yongsheng.Method of Calculating Lower Limit of Buckling Load of Tubular Steel Scaffold Joined by Couplers[J].Architecture Technology,2001,32(8):541.(in Chinese)
[7]敖鸿斐,罗兴隆.双排脚手架整体稳定极限承载力通用计算方法[J].施工技术,2005,34(3):39.
AO Hongfei,LUO Xinglong.A General Calculation Method for the Ultimate Bearing Capacity of Integral Stability of Two-wall Scaffolding[J].Construction Technology,2005,34(3):39.(in Chinese)
[8]CHAN S L,ZHOU Z H,CHEN W F,et al.Stability Analysis of Semirigid Steel Scaffolding[J].Engineering Structures,1995,17(8):568.
[9]WEESNER L B ,JONES H L.Experimental and Analytical Capacity of Frame Scaffolding[J].Engineering Structures,2001,23(6):592.
[10]SYLVESTER A.Contemporary Trends in Formwork Standards:A Case Study[J].Journal of Construction Engineering and Management,1999,125(2):69.
[11]周洪涛,郭志鑫.扣件式钢管满堂脚手架ANSYS受力性能分析[J].施工技术,2013,42(14):98.
ZHOU Hongtao,GUO Zhixin.Mechanical Analysis of Fastener Steel Tube Full-hall Scaffold with ANSYS[J].Construction Technology,2013,42(14):98.(in Chinese)
[12]陈剑波.扣件式钢管脚手架整体稳定性的ANSYS分析[J].水利与建筑工程学报,2011,9(6):105.
CHEN Jianbo.Analysis on Overall Steady-state Load-bearing Capacity of Steel Tubular Scaffold with Couplers Based on ANSYS[J].Journal of Water Resources and Architectural Engineering,2011,9(6):105.
(in Chinese)
[13]田高超.扣件式钢管脚手架稳定承载力影响因素分析[J].建筑安全,2010,25(8):36.
TIAN Gaochao.Analysis of Influential Factors of Stability Bearing Capacity of Steel Tubular Scaffold with Couplers[J].Construction Safety,2010,25(8):36.
(in Chinese)
(责任编辑、校对潘秋岑)
【相关参考文献链接】
何晖,曾凡奎,李宝平,等.高层建筑施工悬挑脚手架研究进展[J].2015,35(1):1.
滕宇思,夏维力.西安市土地综合承载力可持续利用评价[J].2015,35(5):397.
刘慧萍,李宝平.预应力混凝土结构正截面承载力的计算[J].2008,28(2):181.
陈以田.轴向运动屈曲梁非线性振动研究[J].2014,34(4):280.
DOI:10.16185/j.jxatu.edu.cn.2016.06.006
*收稿日期:2015-10-16
基金资助:西安市2014年科技计划项目(CXY1432(1));陕西省教育厅科学研究专项资助项目(14JK1337);陕西省自然科学基础研究计划项目(2014JM2-5079)
作者简介:李宝平(1971-),男,西安工业大学副教授,主要研究方向为结构优化设计、岩土地下工程设计.E-mail:459485782@qq.com.
文献标志码:中图号:TU731.2A
文章编号:1673-9965(2016)06-0461-07
Affecting of Structural Factors of Components and Parts to the Stable Carrying Capacity of Cantilevered Scaffolding
LIBaoping,MUZhaolong,CAIBin,ZENGFankui
(School of Civil Engineering,Xi’an Technological University,Xi’an 710021,China)
Abstract:To determine the stable bearing capacity of cantilevered scaffold under different structural factors,ANSYS finite element software was used to analyze the affecting factors of stability capacity for steel tubular scaffold and buckling of cantilevered scaffold under different structural factors.The results confirm:The change of angle between scissors and the ground has a significant impact on the scaffolding stable capacity,so do the settings of diagonal braces between vertical rods.Along with the length of diagonal braces increases,the stability of scaffold gradually declines under different step distance.The smaller the units wall pieces bearing area is,the higher the overall stability of the scaffold,and the greater the stability of the bearing capacity.
Key words:cantilevered scaffold;structural factors;buckling;stable carrying capacity
