不同顶端结构声屏障绕射声衰减量模拟分析

王金瑞，李舜酩，韩宝坤

（1.南京航空航天大学 能源与动力学院，南京 210000 2.山东科技大学 机械电子工程学院，山东 青岛 266590）



不同顶端结构声屏障绕射声衰减量模拟分析

王金瑞1，李舜酩1，韩宝坤2

（1.南京航空航天大学 能源与动力学院，南京 210000 2.山东科技大学 机械电子工程学院，山东 青岛 266590）

摘要：针对不同顶端结构的声屏障对绕射声衰减量的影响，对四种常见的顶端结构利用国标GB/T17247.2-1998中规定的绕射声衰减量公式进行计算分析，根据0-5 000 Hz频域段内四种结构的绕射量变化曲线选择出最佳构型，结果表明Y形和T形结构绕射声衰减量最多，且几乎相等；然后通过声学软件Virtual Lab对Y形和T形结构进行隔声效果仿真分析，根据声影区内声压级分布情况判断降噪效果，结果显示Y形结构的声压级较T形降低覆盖面积更广，并计算这两种结构的插入损失，结果显示Y形结构较T形障板的降噪效果更好。

关键词：声学；声屏障；顶端结构；绕射量；仿真分析；插入损失

面对日益严重的交通噪声扰民现象，声屏障在道路交通噪声的控制上所表现出来有效的吸声隔声性能及其广阔的发展前景引起了越来越多学者和机构的关注。国外对声屏障研究主要是针对其声学特性和几何形状研究了声波的传播规律和声屏障的插入损失，Van Leeuwen[1]测试了14种不同的声屏障模型，对比后发现都有各自突出的声学性能。Salomons[2]研究了在空气折射的情况下声屏障插入损失模型，比较声波经过声屏障时的传播，经由类比法得到模型的精度。国内研究主要针对噪声的声源和声屏障的声学结构研究，张增海[3]根据国标(GB/ T27347.4-2009)中规定的声屏障对点声源插入损失的计算公式[4]，将列车噪声设置为线声源，设铁路两侧声屏障的长度为无限长，运用Matlab编程计算，计算与测量及理论分析结果对比，表明该模型能达到预期效果。高莉萍[5]等结合铁路声屏障声学结构设计时涉及到的问题，研究了声屏障声学结构设计原则和几种不同绕射声衰减量的理论计算方法。

声屏障不同顶端结构对绕射声会产生不同的影响，所以通过研究不同顶端结构绕射声衰减量的分布情况[6]可以适当选择出应用在城市居民区附近的最佳构型，居民区一般都为高层建筑，因此对声屏障在相对较高位置的降噪性能有一定要求。

本文以声屏障顶端结构作为研究对象，探究声波在遇到声屏障时的绕射声衰减，通过对不同顶端结构的分析选择出最佳结构，也对声屏障的研究应用提供一些理论依据和数据。

1声屏障构型选择

声屏障高度设计一般在3 m～5 m，过高的声屏障会对人们视觉产生压迫感，相对较低的障板上添加不同顶端绕射结已构成为当今声屏障结构设计的重要发展趋势。本文设计以3 m为基本高度[7]，对不同绕射结构进行绕射声衰减量分析。

选取声源的位置在声屏障内侧距障板水平距离为4 m处，接收点在障板背侧后20 m处，高度均在水平地面上，根据我国交通噪声频谱特点设置声波频率范围为100 Hz～5 000 Hz[8]。当声源为点声源时，声屏障可视为无限长声屏障。根据GBT 17247.2-1998[9]中规定其绕射声衰减计算公式为：DS=10lg[3+(C2/λ)C3zKmet]dB。式中：C2等于40，不考虑地面反射影响，C3等于1，单绕射；

λ——声波波长为声速，f为频率；

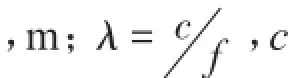
z——声程差，m；

Kmet——气象影响修正因子，等于1。

1.1直立型声屏障

由图1得，A=5 m，B=20.2 m，d=24 m得

z=A+B-d=5+20.2-24=1.2 m

图1　直立型声波绕射路径

1.2内倾型声屏障

由 图 2得 ，A=4.615 m ，B=20.715 m ，d=24 m得

z=A+B-d=4.615+20.715-24=1.33 m

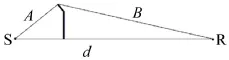
图2　内倾型声波绕射路径

1.3 Y形声屏障

由 图 1.3得 ，A=4.814 m ，B=20.585 m ， d=24 m得

z=A+B-d=4.814+20.585-24=1.399 m

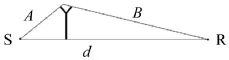
图3　Y形声波绕射路径

1.4 T形声屏障

由 图 4得 ，A=4.811 m ，B=20.582 m ，d=24 m得

z=A+B-d=4.811+20.582-24=1.393 m

图4　T形声波绕射路径

将菲涅尔数代入绕射声的衰减量的计算公式DS=10lg[3+(C2/λ)C3zKmet]dB

经Matlab计算得如图5。

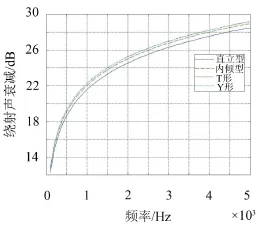
图5　四种声波绕射衰减量结果对比

由图1.5可知，在声屏障后水平距离20 m处随着频率的增加，四种不同顶端结构的声屏障的绕射声衰减量都呈上升趋势，在低频区域上升趋势很快，到高频区域上升趋势减缓，到5 000 Hz处都能达到28 dB以上。其中Y形和T形的绕射声衰减最多且几乎相等，因此在下文中主要对Y形和T形结构声屏障进行仿真分析并确定结构选形。

2　声屏障声学结构仿真

采用声学软件Virtual Lab对Y形和T形结构的声屏障进行仿真分析，观察声屏障背后区域的声场分布情况，根据结果选择出适合用于城市道路两侧的声屏障顶端结构。

2.1声屏障仿真条件设定

（1）噪声源条件设置

将道路交通噪声假设成一条线声源，根据交通噪声频率段特点，线声源的频率取500 Hz[10]，障板离线声源的水平距离是4 m。

（2）声屏障布置

假定声屏障水平长度是200 m，计算在中间位置100 m处剖面的声影区，这是为了消除障板两端的侧向声绕射影响。声影区的范围为障板后水平距离50 m高度30 m内，研究在此范围内的声压级的分布情况，符合交通噪声对两侧居民区噪声波及范围的实际状况。本文在研究声屏障的声压级分布上是选取与声屏障垂直的立面进行研究，布置情况如图6，线声源距离障板的水平距离为4 m，竖直网格是要分析的声影区的声压分布剖面。同障板的竖面垂直，宽为50 m，高为30 m。

图6　声屏障降噪模拟分析布置图

2.2屏障背后声场分布仿真结果

（1）无声屏障时噪声传播

图7是在未布置声屏障时的声压分布情况，以此为基础对比布置了声屏障之后的声场分布情况。

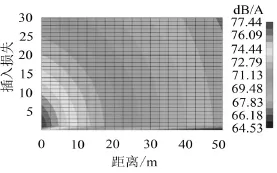
图7　未设置声屏障时交通噪声声压级分布

（2）Y形声屏障仿真结果

由图8可以看出，相比于未布置声屏障的情况，声压分布在大范围内都有所降低，并且表示低声压级的深黑色区域在50 m处要高出声屏障的高度。

图8　Y形声屏障降噪效果模拟声压级分布

（3）T形声屏障仿真结果

由图9可以看出，相比于Y形声屏障，表示低声压级的深黑色区域分布比较紧凑，而且都集中在小于3 m高的区域内，即都没有超出T形声屏障的高度。

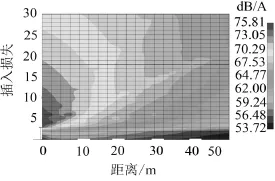
图9　T形声屏障降噪效果模拟声压级分布

3降噪仿真结果分析

由图7、图8、图9可以看出，在声屏障后水平距离20 m处Y形和T形声屏障降噪量都能达到17 dB以上，随着水平距离的不断增加降噪量逐步增加。对比这两种不同的声屏障顶部结构，可以看出其后面形成的声压分布也有很大差异，Y形形成的声压级分布的层次相比T形更清晰明显，而T形声压级的分布相对比较集中，且在高度3 m以下的声压级分布都相对较低，而在3 m以上降噪效果则不明显，所以T形声屏障适合用于高速公路两侧，濒临城镇农村建筑周围。而Y形声屏障在较高的高度也有较好的降噪效果，即其声压级降低的覆盖面积更广，所以适用于城市道路两侧，濒临高层建筑的地区。

3.1插入损失计算

为更直观地观察声压级的分布情况，引入插入损失的计算。插入损失（IL）是指保持噪声源、地形和气候条件不变的情况下安装声屏障前后受声点处测得声压级之差，如下式所示[11]

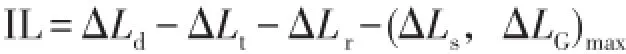
ΔLd——绕射声衰减；

ΔLt——透射声衰减；

ΔLr——反射声衰减；

ΔLs——障碍物声衰减；

ΔLG——地面吸收声衰减。

表1列出Y形和T形声屏障在10 m、20 m、30 m、40 m、50 m等不同距离，高度2 m～20 m范围内插入损失。列出的插入损失为声影区内数据，对比这两种不同顶端结构声屏障的降噪效果。

由表1可知，在高度低于障板高度的位置，不同距离隔声降噪效果较好的是T形结构。如在高度2m，距离30 m时，T形结构插入损失为14.10 dB，比Y形结构高0.65 dB。随着高度增加到2 m以上，降噪性能显著下降，如距离30 m时，高度2 m降噪量为14.10 dB，而高度8 m时，降噪量降为6.35 dB，插入损失下降量达到7.75 dB。而Y形声屏障在距离30 m，高度从2 m增加到8 m时，插入损失降低量为4.10 dB。因此T形结构适用于低位置降噪。

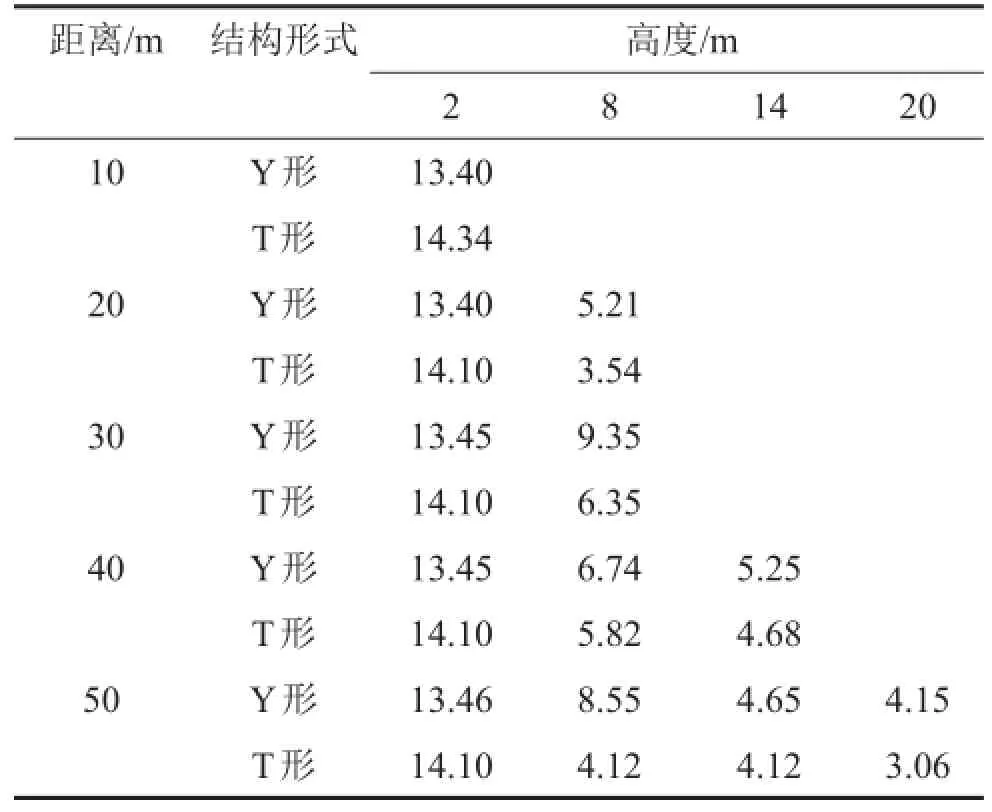
表1　两种结构插入损失比较/dB

而Y形声屏障在较高高度仍有较好的降噪效果，随高度增高，插入损失下降比T形少。如在50 m距离，高度20 m的位置，插入损失比T形声屏障高1.09 dB，测点高度由2 m升高到20 m时，Y形声屏障插入损失变化量为9.31 dB，T形声屏障插入损失变化量为11.04 dB。因此Y形声屏障在高度增加时插入损失降低量较小，比较适用于道路两边较高的建筑，即在较高的位置仍然有较好的降噪效果。

究其原因，因为Y形声屏障的顶部分叉结构，可以使声波在分叉处发生衍射，同时在分叉处又可经历多次反射，声能得到消耗，所以在较高位置有较好降噪效果。而T形的顶部结构向两端延伸，在较低位置对声波绕射遮蔽较多，因此有较好隔声效果，随着高度上升，顶端遮蔽功能越来越弱，所以在较高位置隔声效果较差。

3.2仿真结果对比

表2列出了文献[12]使用声学仿真软件Raynoise得出的数据。

由表2可知，各组仿真数据均比表1数据略低，随水平距离和高度的变化趋势与表1相同。如在距离为30 m，高度从2 m增加到8 m时，Y形和T形的插入损失降低量分别为3.3 dB和7.1 dB，与表1的4.10 dB和7.75 dB数值近似。同样在距离50 m处，测点高度由2 m升高到20 m时，Y形声屏障插入损失变化量为7.9 dB，T形声屏障插入损失变化量为10.2 dB。与表1的9.31 dB和11.04 dB数值近似。因此结论相同，即T形结构适用于低位置降噪，Y形结构适用于高位置降噪。

表2　文献[12]的两种结构插入损失比较/dB

文献[12]中的仿真数据都略低于本文的仿真计算数据，原因可能是与Raynoise降噪原理的局限有关。Raynoise在低频或小尺度空间的模拟效果比较差，这必然会大大缩小其应用范围。同时，它只能给出简单声源在给定点的模拟结果，而对于运动声源、分布式声源、指向性声源以及更为复杂的情况则有局限。

综上所述，城市道路两侧的声屏障对较高建筑的降噪效果要求高，所以更适合采用顶端结构为Y形的声屏障。

4结　语

（1）声屏障的不同顶端结构对绕射声衰减量有较大影响，计算声屏障后一固定点的绕射声衰减量随声波频率的变化情况，可以选择出最佳构型；

（2）利用声学软件Virtuallab可仿真得到声屏障背后声影区的声压分布情况，对比分析可得不同构型在不同水平位置和不同高度处的降噪效果；

（3）通过插入损失的计算验证了T形结构适用于低位置降噪，Y形结构适用于高位置降噪。

参考文献：

[1]J J A Van Leeuwen.Noise prediction models to determine the effect of barriers placed alongside railway lines[J]. Journal of Sound and Vibration,2010,193(1):269-276.

[2]ErikM,Salomons.Noisebarriersinarefracting atmosphere[J].AppliedAcoustics,2013,47(3):217-238.

[3]张增海,王重实.无限长声屏障对运行列车噪声降噪模型研究[J].噪声与振动控制，2012，32(1)：12-14.

[4]宫本贤.声屏障隔声量的计算方法与设计[J].噪声与振动控制，2007，27(3)：41-44.

[5]高莉萍，刘达德.铁路声屏障插入损失的研究[J].噪声与振动控制，2008，28(4)：28-31.

[6]彭立新，胡卫保.道路声屏障设计探讨[J].冶金矿山设计与建设，2013，6(3)：509-515.

[7]王孚懋，任勇生，韩宝坤.机械振动与噪声分析基础[M].北京：国防工业出版社，2010.

[8]董建昆.城市轨道交通声屏障设计探讨[D].噪声与振动控制，2009，29(6)：33-37.

[9]马大猷.噪声控制学[M].北京：科学出版社，2013.

[10]彭立新，胡卫保.道路声屏障设计探讨[J].冶金矿山设计与建设，2013，6(3)：509-515.

[11]章力，郑长聚.声屏障对交通噪声的A计权插入损失[J].同济大学学报，2010，17(2)：265-271.

[12]陈继浩.隔声屏障结构声学模拟、设计与性能优化应用研究[J].北京：中国建筑材料科学研究总院，2010.

要研究方向：车辆振动与噪声控制。

E-mail:smli@nuaa.edu.cn

中图分类号：O422

文献标识码：A

DOI编码：10.3969/j.issn.1006-1335.2016.01.027

文章编号：1006-1355(2016)01-0125-04+132

收稿日期：2015-09-21

作者简介：王金瑞（1989-），男，山东省滕州市人，博士生，主

通讯作者：李舜酩，男，博士生导师。

SimulationAnalysis of Sound DiffractionAttenuation of Different Sound Barrier’s Top Structures

WANG Jin-rui1,LI Shun-ming1,HAN Bao-kun2

（1.College of Energy and Power Engineering,Nanjing University ofAeronautics andAstronautics, Nanjing 210000,China; 2.College of Mechanical and Electrical Engineering,Shandong University of Science and Technology, Qingdao 266590,Shandong China）

Abstract:In order to study the influence of different top structures of the sound barriers on the effect of sound diffraction attenuation,the attenuation formula in GB/T17247.2-1998 standard was used to analyze and calculate the diffraction attenuation of four kinds of common apex structures.The optimal configuration was selected according to the curve of diffraction attenuation change in 0-5 000 Hz frequency range.The results show that the Y-type and T-type structure’s diffraction attenuations are the largest and nearly the same.Then,using the acoustic software Virtual Lab,the sound insulation simulation was done for the Y-type and T-type structures.And their noise-reduction effects were determined according to the distribution of sound pressure level in the acoustic shadow.The results show that the sound pressure level’s reduction area of the Y-type structure is wider than that of the T-type.Then,the insertion losses of the two structures were calculated.The results show that the noise reduction effect of the Y-type structure is better than that of the T-type.

Key words:acoustics;noise barrier;top structure;diffraction attenuation;simulation analysis;insertion loss