UPFC的暂态分析及电容选取方法
2016-08-03唐立华杭州凯达电力建设有限公司杭州300陕西省电力设计院有限公司西安70054
唐立华,申 滔,吕 锋(.杭州凯达电力建设有限公司,杭州 300;.陕西省电力设计院有限公司,西安 70054)
UPFC的暂态分析及电容选取方法
唐立华1,申 滔2,吕 锋1
(1.杭州凯达电力建设有限公司,杭州 311100;2.陕西省电力设计院有限公司,西安 710054)
摘要:为了保证统一潮流控制器的性能,维持直流侧电压的稳定至关重要,需要选取合适的电容参数。本文基于瞬时电压和电流矢量理论,首先对统一潮流控制的暂态过程进行分析,证明暂态过程中流经串联侧的有功存储为线路电感的磁场能,由此推导出电容选取的依据。然后在MATLAB中搭建含有统一潮流控制器的单机无穷大系统仿真模型,获得暂态过程的时域波形。结果表明若由直流侧电容提供暂态能量,其存储电能的变化量与线路电感的磁能变化量相同,与理论分析相吻合,为实际电容的设计提供了重要依据。
关键词:统一潮流控制器;暂态分析;直流侧电容;单机无穷大系统
自1991年美国西屋科技中心的Gyugyi博士提出统一潮流控制器UPFC(unified power flow control⁃ler)的概念以来,不少学者开始致力于对它的研究[1]。UPFC作为柔性交流输电家族中最复杂的也是最有吸引力的一种补偿器,能够对电力线路上的阻抗,相角及有功和无功进行任意组合控制,集多种功能于一身,具有很强的灵活性。美国电力公司于1998年在肯塔基东部INEZ地区安装了世界上第1台UPFC,它作为世界上最大的逆变器,具有640 MV·A的控制能力,得到世界电力工业界的广泛关注[2]。
现有文献大多致力于UPFC潮流控制的效果及稳定性的改善[3-13],鲜有文献研究UPFC的暂态行为及装置参数的选取。UPFC快速潮流控制会引起直流侧电压的波动,因为串联侧注入的电压与线路电流会产生一定的有功功率,这部分功率在暂态过程中会流入(或流出)直流侧电容。若该功率数值较大,则会引起直流侧电压的骤升(或骤降),而直流侧的过电压不利于UPFC的安全运行。因此有必要选取合适的电容值以避免其发生。
为了对UPFC潮流控制的暂态过程进行分析,本文基于瞬时电压、电流矢量理论,从原理上讨论了流经串联侧的有功功率,分析结果表明暂态过程中流出串联侧的有功功率转移至线路电感中,这部分功率若由直流侧电容提供,则电容在暂态过程中释放的电能等同于线路电感存储的磁能,电容选择的依据可由此获得。
1 UPFC的数学模型和控制原理
UPFC的基本结构如图1所示。它由两个电压源型的变流器组成,连接两个变流器的直流环节由两个变压器组成。图1中Ls和Rs是并联变流器的输入电感和电阻,L和R是传输线路的电感和电阻,C为直流侧电容。相关变量的物理意义见表1。

图1 UPFC的基本结构Fig.1 Basic structure of UPFC

表1 相关变量及其物理意义Tab.1 Relevant variables and their physical meanings
当并联变流器单独运行时,相当于静止同步补偿器STATCOM(static synchronous compensator),而当串联变流器单独运行时,相当于静止同步串联补偿器SSSC(static synchronous series compensator)。并联变流器主要负责进行无功补偿和维持端点电压,同时根据串联部分需要来提供有功支持以维持直流环节的有功功率平衡。串联变流器系统注入幅值和相角均可调的电压,实现对传输线路上的潮流控制。
1.1 UPFC的并联侧分析
根据图1列出UPFC并联侧的状态方程为
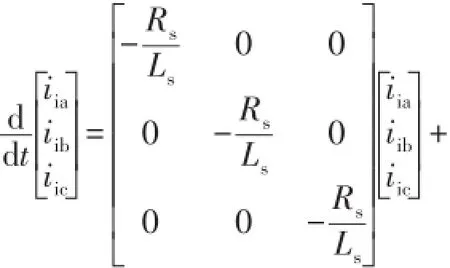

令d轴以vs空间矢量定向(即 vsd= ||vs,vsq=0),对式(1)做Park变换,得到两相同步旋转坐标系下的状态方程为

式中ω为坐标系的旋转角频率,ω=dθ/dt,θ可由锁相环PLL(phase locked loop)测得,同步旋转时ω为电网基准角频率。为实现对iid、iiq的解耦控制,式(2)改写为
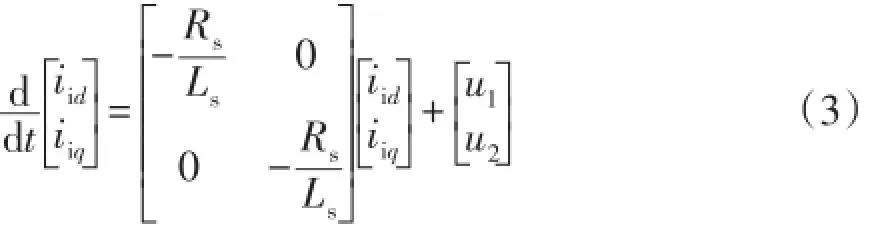
其中

由式(4)和式(5)得到控制律为

根据式(6)和式(7),可实现对送电端电压vs和直流侧电压vdc的前馈解耦控制,如图2所示。
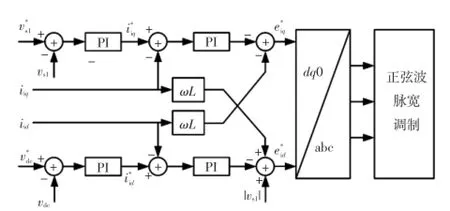
图2 UPFC并联侧控制框图Fig.2 Control block diagram of UPFC shunt converter
1.2 UPFC的串联侧分析
类似地,令d轴以vs空间矢量定向,可列出dq轴系下线路电流的状态方程为
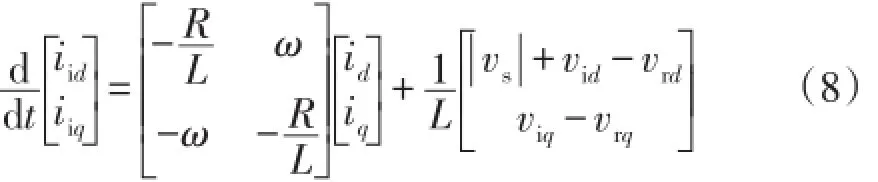
由于ωL≫R,可得式(8)稳态解为

因送电端与受电端的电压幅值近似相等,即

设功率角为δ,则有

忽略变流器自身损耗,可推得输出的有功功率Po和无功功率Qo分别为

将式(12)和式(13)改写为增量形式,即
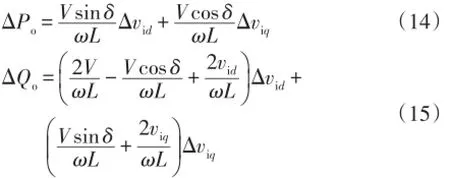
通常,功率角δ不超过30°,则cosδ>sinδ。因此,从式(14)和式(15)可知,Δviq对Po的影响较大,Δvid对Qo的影响较大。这也是诸多文献中,通过调节viq控制Po,调节vid控制Qo的原因。UPFC串联侧控制框图如图3所示。
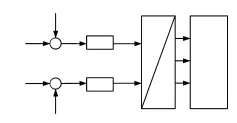
图3 UPFC串联侧控制框图Fig.3 Control block diagram of UPFC series converter
2 暂态分析与电容选取
2.1 潮流的暂态分析
直流侧等效电路如图4所示。

图4 直流侧等效电路Fig.4 DC-link equivalent circuit
由瞬时功率平衡可知

式中:PC为直流侧电容吸收的功率;Psh为由并联侧变流器传输的有功功率;Pi为串联侧注入系统的有功功率。
式(8)与式(18)联立,解得
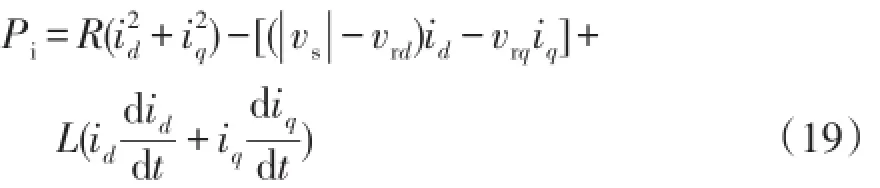
式(19)表明了暂态过程中,配有UPFC的电力线路有功功率的构成,前两项为稳态功率,第3项为暂态功率,如图5所示。

图5 暂态过程的UPFC潮流Fig.5 Power flow of the UPFC in transient states
式(19)第1项为线路电阻R消耗的有功功率;第2项表征送电端与受电端的有功功率之差,大小依赖于vs和vr的幅值及相位差;第3项为流入线路电感L的功率。通常,第3项的值远小于前两项之代数和,但在潮流快速变化(即潮流控制响应速度很快)的情况下,第3项的值较大,不能忽略。
假设暂态从t=0时刻持续至t=T,id从Id0变为Id1,iq从Iq0变为Iq1。对式(19)的第3项做积分可得

式中,ΔW为t=0至t=T时间内电感L存储能量的增量,其值取决于线路电流幅值的变化。
假设三相电流对称正弦,即
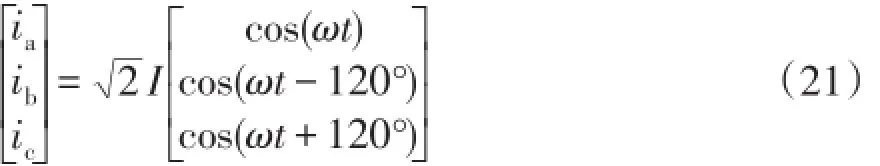
式中,I为电流有效值。令d轴以i空间矢量定向,对式(21)做Park变换,得

将式(22)代入式(20),得

式中,I0和I1分别为t=0和t=T时的电流有效值。式(23)将作为直流侧电容选取的重要依据。
2.2 电容的选取
由式(16)和式(19)可知,传输至电感的电能是由直流侧电容释放或并联侧变流器提供,若由并联侧变流器经串联侧向线路电感提供式(19)中所有能量,则直流侧电压几乎没有波动,此时所需的并联侧变流器容量较大。
另一方面,若由直流侧电容提供暂态能量,则所需的并联侧容量较小,略大于式(19)的稳态功率(前两项之代数和)即可。此时,直流侧电压会根据暂态中释放或吸收的能量多少而产生波动,因此有必要选择合理电容值以抑制其波动。
假设直流侧电容提供暂态功率,而并联侧变流器仅提供稳态有功。直流侧电压由Vdc0变为Vdc1,则电容释放的能量ΔWdc为

式中,ΔWdc应等于式(23)的ΔW。定义电压变化率ε 为

结合式(23)~式(25)可得

由于ε2≪2ε,式(26)可近似为

由式(27)可知,所需的电容值正比于线路电感,因此远距离传输系统需要较大的电容。
3 仿真验证
为了验证上述理论,搭建单机无穷大系统仿真模型,发电机、变压器经双回220 kV,100 km输电线路与无穷大母线相连,发电机发出功率为100 MW,UPFC安装在其中1条输电线路上,系统结构图及参数如图6所示。相关参数及取值如表2所示。
表2中线路电感和电阻的值取自文献[13]。由表2可推得,线路电流的基准值Ib=0.251 kA,假设线路有功潮流受UPFC控制,由50 MW增至80 MW,则UPFC所在线路的电流有效值由0.125 5 kA变为0.200 8 kA。为了使电容电压在暂态过程的变化率不超过10%,由式(27)可知所需的电容为

图6 含UPFC的单机无穷大系统Fig.6 Single-machine infinitive bus system with UPFC
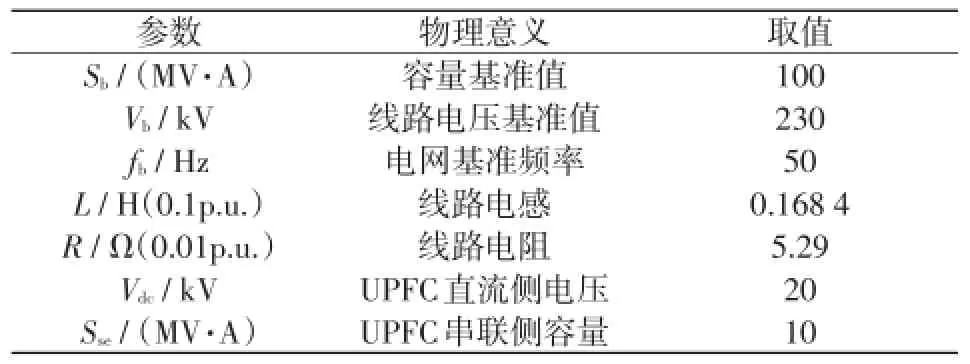
表2 相关参数及取值Tab.2 Relevant parameters and their values
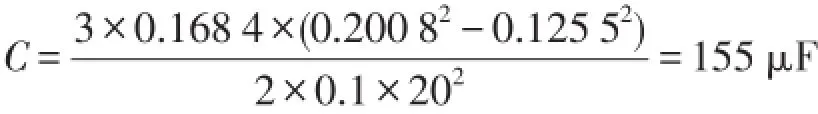
仿真参数取C=200 μF。
假设由并联侧变流器向线路电感提供式(19)中所有能量,所需的并联侧容量较大,取并联侧变流器传输的容量Ssh=5 MVA,即串联侧容量Sse的。仿真10 s时UPFC进行潮流控制,由原来的自然功率50 MW增至80 MW,获得仿真时域波形如图7所示。
由图7(a)~(e)可知,仿真10 s之后UPFC将线路有功潮流由50 MW控制为80 MW。图7(f)表明,暂态过程中流经串联侧的有功功率约为0.9 MW,稳态之后为0.68 MW,而选取的并联侧变流器容量为5 MVA,可提供式(19)中所有功率,故直流侧电容电压波动很小,如图7(g)所示。
假设由直流侧电容提供式(19)中的暂态功率(即第3项),并联侧变流器只提供式(19)中的稳态功率(即前两项之代数和,约0.68 MW),将其容量Ssh改为0.7 MW,再次进行仿真。可发现,其他变量波形与图7基本相同,只有直流侧电压波形不同,如图8所示。
由图8可知,暂态过程中直流侧电压由20 kV降至18.4 kV,可解得


图7 仿真时域波形Fig.7 Time domain simulation waveforms

图8 直流侧电压波形Fig.8 Time domain waveforms of DC-link voltage
ΔWdc≈ΔW,与理论分析吻合,即暂态过程中直流侧电容存储的电能转移并存储为线路电感的磁能。
4 结论
本文基于瞬时功率理论,分析并仿真验证了UPFC潮流控制的暂态过程,结果表明流经串联侧变流器的有功功率传输至线路电感。这部分能量可由并联侧变流器提供,也可由直流侧电容提供。相关结论总结如下。
(1)快速的潮流控制会产生一定的有功功率,存在于串联侧与线路电感之间,潮流控制的响应速度越快,这部分有功功率的值越大。
(2)为了保持直流侧电压恒定,所需的并联侧变流器容量是暂、稳态功率之和。若由直流侧电容提供暂态功率,则并联侧只需提供稳态功率,其容量较小。
当UPFC安装于长线路时,仅靠电容提供所有的暂态功率不切实际,此时需要并联侧变流器分担部分暂态功率,或对串联侧的潮流控制响应速度加以限制。本文的理论分析与仿真为UPFC的电容选取提供了依据。
参考文献:
[1]Gyugyi L.Unified power-flow control concept for flexible AC transmission systems[J].IEE Proceedings-Generation,Transmission and Distribution,1992,139(4):323-331.
[2]Mehraban A S,Edris A,Schauder C D,et al.Installation,commissioning,and operation of the world's first UPFC on the AEP system[C]//IEEE International Conference on Power System Technology.Beijing,China,1998:323-327.
[3]Jiang Zhenhua.Design of a nonlinear power system stabi⁃lizer using synergetic control theory[J].Electric Power Sys⁃tems Research,2009,79(6):855-862.
[4]Cai Lijun,Erlich Istvan.Simultaneous coordinated tuning of PSS and FACTS damping controllers in large power sys⁃tems[J].IEEE Trans on Power Systems,2005,20(1):294-300.
[5]Leung J S K,Hill D J,Yixin Ni.Global power system con⁃trol using generator excitation,PSS,FACTS devices and capacitor switching[J].International Journal of Electrical Power and Energy Systems,2005,27(5/6):448-464.
[6]Furini M A,Pereira A L S,Araujo P B.Pole placement by coordinated tuning ofpowersystem stabilizersand FACTS-POD stabilizers[J].International Journal of Elec⁃trical Power and Energy Systems,2011,33(3):615-622.
[7]蔡松,段善旭,蔡礼(Cai Song,Duan Shanxu,Cai Li).基于交叉耦合与交叉解耦的UPFC控制性能对比(Com⁃parison of UPFC performance between crossing coupling and decoupling controls)[J].电力自动化设备(Electric Power Automation Equipment),2007,27(5):45-49.
[8]朱鹏程,刘黎明,刘小元,等(Zhu Pengcheng,Liu Lim⁃ing,Liu Xiaoyuan,et al).统一潮流控制器的分析与控制策略(Analysis and study on control strategy for UPFC)[J].电力系统自动化(Automation of Electric Power Sys⁃tems),2006,30(1):45-51.
[9] Mishra S.Neural-network-based adaptive UPFC for im⁃proving transient stability performance of power system[J].IEEE Trans on Neural Networks,2006,17(2):461-470.
[10]杜文娟,秦川,王海风,等(Du Wenjuan,Qin Chuan,Wang Haifeng,et al).UPFC控制的协调设计 变参数开环解耦控制方法(Coordinated design of UPFC— Avariable-parameter open-loop decoupling method)[J].电力系统自动化(Automation of Electric Power Systems),2008,32(8):19-23.
[11]陈剑平,李林川,张芳,等(Chen Jianping,Li Linchuan,Zhang Fang,et al).基于PSASP的UPFC潮流控制建模与仿真(Modeling and simulation of power flow control for UPFC based on PSASP)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26(2):66-70.
[12]谢桦,梅生伟,徐政,等(Xie Hua,Mei Shengwei,Xu Zheng,et al).统一潮流控制器的非线性控制和对电力系统稳定性的改善(Nonlinear control for UPFC to im⁃prove transient stability of power systems)[J].电力系统自动化(Automation of Electric Power Systems),2001,25 (19):1-5.
[13]Kundur P.Power System Stability and Control[M].New York:McGraw-Hill,1994.
唐立华(1979—),男,本科,工程师,研究方向为电力系统及其自动化。Email:1146675738@qq.com
申 滔(1988—),男,硕士,工程师,研究方向为电力电子技术在电力系统中应用。Email:xtst200373@126.com
吕 锋(1985—),男,本科,工程师,研究方向为电力系统及其自动化。Email:zjlvfeng@163.com
中图分类号:TM761
文献标志码:A
文章编号:1003-8930(2016)07-0063-05
DOI:10.3969/j.issn.1003-8930.2016.07.012
作者简介:
收稿日期:2014-09-10;修回日期:2015-12-02
基金项目:输配电装备及系统安全与新技术国家重点实验室自主研究项目(2007DA10512711205)
Transient Analysis of UPFC and Selection of Capacitor
TANG Lihua1,SHEN Tao2,LYUFeng1
(1.Kaida Electric Power Construction Co.Ltd in Hangzhou,Hangzhou 310000,China;2.Shaanxi Electric Power Design Institute,Xi’an 710054,China)
Abstract:In order to guarantee the performance of unified power flow controller(UPFC),it is essential to maintain the required voltage at DC side and select appropriate capacitor parameter.Therefore,based on instantaneous voltage and current vectors theory,a transient analysis of UPFC in power flow control is presented firstly.It is clarified that the ac⁃tive power flowing through the series convertor is stored in the line inductance as magnetic energy during transient states,which derives the basis for choosing capacitor.After that,a single-machine infinite bus system model with UP⁃FC is simulated in MATLAB,and time domain waveforms in transient states are attained.The results show that,if the transient energy is supplied by the capacitor,the variation of electrical energy equals to that of magnetic energy in the line inductance,which coincided with theoretical analysis and can provide important basis for the design of DC-link ca⁃pacitor.
Key words:unified power flow controller;transient analysis;DC-link capacitor;single machine infinite bus system
