大型海上风电场集电系统网络拓扑优化设计
2016-08-03卢永魁黄玲玲魏书荣山东电力工程咨询院有限公司济南5003上海电力学院电力与自动化工程学院上海00090
樊 潇,卢永魁,黄玲玲,魏书荣(.山东电力工程咨询院有限公司,济南 5003;.上海电力学院电力与自动化工程学院,上海 00090)
大型海上风电场集电系统网络拓扑优化设计
樊 潇1,卢永魁1,黄玲玲2,魏书荣2
(1.山东电力工程咨询院有限公司,济南 250013;2.上海电力学院电力与自动化工程学院,上海 200090)
摘要:大型海上风电场集电系统由于需要采用大量的海底电缆及其他海上设备,其成本在海上风电场投资中占据较大比例。本文在构建大型海上风电场集电系统经济性模型的基础上,为了解决影响各因素之间相互联系又相互制约的关系,采用由上而下的方法将经济性优化问题分解为海上变电站优化与风机连接优化两个相对独立的部分。此外,为了实现算法的工程实用性,本文也充分考虑了海底电缆的非交叉性要求以及特殊海底条件造成的规避区情况。图论方法被用于该优化问题,算例结果显示该方法是合理有效的。
关键词:大型海上风电场;集电系统;图论;模糊C均值算法
作为一种清洁的可再生能源,风能是能源可持续发展的战略选择。将风力发电作为应对全球气候变化的重要手段已经是世界范围内的共识。据全球风能理事会统计,截止到2014年底,全球海上风电装机累计约8 771 MW[1],预计到2020年,将达到51.2 GW。从世界各国海上风电的发展与规划来看,建立远海、大型海上风电场已经成为海上风电开发的主要方向[2]。现有已并网运行的最大规模海上风电场是London Array海上风电场,该风电场由175台风机构成,总装机容量达到630 MW,而规划中的最大规模海上风电场Blekinge装机容量将达到2 500 MW。更大规模的海上风电场与更远距离的电能传输,对海上风电场集电系统的经济型与可靠性提出了更高的要求。
近年来,不少学者开始对此进行研究。海上风电场由于受地理环境影响较小,海底电缆路由具有更加多样的选择性。文献[3]介绍了风电场内部风机之间常用的几种拓扑连接形式,如放射性和环形是目前最常用的两种连接方式。文献[4-6]以风电场集电系统电气设备成本经济性优化为目标,通过建立数学模型,优化集电系统的连接方式。另外,文献[4,7-8]还考虑了海上变电站容量和数量的影响,建立了基于大型海上风电场投资成本最小的数学模型,并采用遗传算法优化集电系统的规划。这些文献大都侧重于如文献[4]所描述的离散变量的优化部分或优化算法的研究,对集电系统所表现出来的图形拓扑性质、拓扑约束及其对离散变量的影响研究相对较少,甚至如文献[8]的优化结果在保证海缆线路不相互交叉上存在不足。
本文在上述研究基础上,针对海上风电场拓扑形式相对自由的特点,充分考虑集电系统的图形拓扑特点与约束,将集电系统优化问题从上而下的分解为海上变电站优化与风机连接优化两个相对独立的部分,并采用图论的方法对问题进行求解。最后的算例表明,该方法是合理有效的。
1 大型海上风电场集电系统优化模型
海上风电场集电系统包括电力传输系统、海上变电站和中压海缆网络3个部分。结合文献[4]可以将海上风电场集电系统总投资成本模型表示为

式中:Ecost为风电场电气连接的总投资费用;Cmtr为风机出口箱变及相关开关设备成本;Csub为海上变电站投资成本;Ccab为海底电缆成本费用;Coth为其他施工、管道交叉以及海域使用费用等;Sbranch为电气接线每一条支路上传输的视在功率;Smax为每条支路所能传输的最大视在功率。
文献[4]对该模型进行分析整理,将影响海上风电场集电系统经济性的7个重要因素归纳为离散变量函数的最优求解和线路拓扑优化两类问题,并采用遗传算法对其中的离散变量优化问题进行求解。但是该文献并未对线路拓扑连接的优化及其对集电系统设计的影响展开进一步的分析。而实际上拓扑连接的方式不仅决定了所选电气设备的容量,同时也可能影响海上变电站的数量与分布。
为了充分描述海底电缆的拓扑连接对集电系统成本的影响,本文在对放射型的集电系统进行研究的基础上,从图论的角度出发,将海上风电场中的每段海底电缆线路视为图论中的“边”,风机视为“节点”,每段海底电缆的价格则是各条“边”的加权。因此,一个海上风电场集电系统可以视为由许多以海上变电站为“根”节点的“树”型结构构成的一个连通图。海底电缆的成本计算可以表示为

式中:M为海上变电站的数量,即该海上风电场内部变电区域的数量;Ni为第i个变电区域中,以该海上变电站为“根”的“树”的数量,即该变电区域中的风机被划分的串数;Lij为第j棵树所包含的边的数量,即该串风机上的电缆的数量;lijk与cijk分别为第i个变电区域中第j棵树的第k条边的长度与价格;sij与cij分别为第i个变电区域的第j棵树中离变电站最近的风电机组与该海上变电站之间电缆的长度与价格。这里的电缆长度由相互连接的两个节点之间的距离并考虑一定的裕量来决定。
从式(2)可以看出,海底电缆的长度及其价格都与集电系统的连接拓扑直接相关。同时,考虑到海上风电场风机为固定分布但是海上变电站位置具有可调节性的特点,海上风电场集电系统可行解的组合空间非常大。以一个装设有s台风机的海上风电场为例,在不考虑其他各种离散变量的影响下,集电系统的可行拓扑方案也有ss-2种。其优化问题求解的时间与空间复杂度相当高。
2 大型海上风电场集电系统经济性优化算法
本文对海上风电场的工程特点和约束条件进行分析,发现海上风电场集电系统有以下特点。
(1)适用于海上风电场集电系统的电压等级有限,海上风电场高压侧大都采用220 kV(其他可选范围目前仅限110 kV和500 kV),低压侧大都采用35 kV。即电压变量的可优化空间较小。
(2)海底电缆大都采用标准化生产,可供选择的电缆型号较为有限,如35 kV海底电缆通常在50~400 mm2之间,可承载3 MW机组约4~11台。这极大地约束了拓扑空间的连接方式,即“每串”风机的数量变化范围。
(3)变压器情况与海底电缆相似,一个大规模海上风电场中的海上变电站数量非常有限,即由海上变电站决定的风电机组分区数量也是有限。
本文在此基础上对大型海上风电场集电系统优化设计问题进行了分割,将这些可变化范围不大的离散变量采用全局搜索的方式寻优,其基本流程如图1所示。
这个算法实际上将大型海上风电场集电系统设计分成两大块:变电站优化与风机连接拓扑优化。4个相对独立的部分:确定海上变电站的数量与位置并将风机进行分区(即变电区域优化)、考虑到每个变电区域内海底电缆路由的实际约束生成可行海底电缆敷设路径、将每个变电区域内的风机按“串”分组、风机间优化连接(风机连接优化)。因此,在枚举算法的条件下,集电系统优化问题便演变为在给定离散变量下的连接拓扑优化问题。
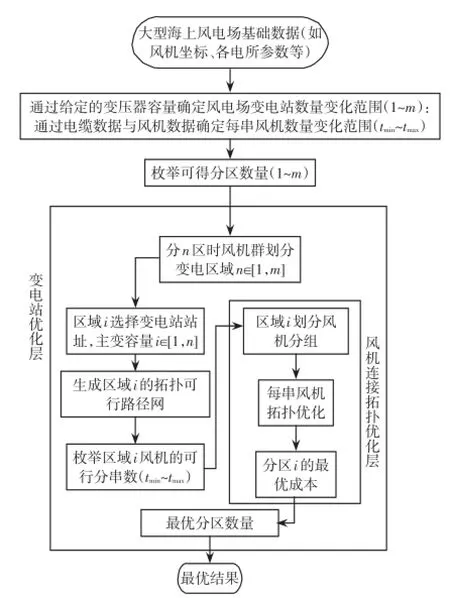
图1 大型海上风电场集电系统优化算法流程Fig.1 Flow chart of optimization of electrical collection system in large-scale offshore wind farm
2.1 大型海上风电场风机机群变电区域划分
对于一个小型的海上风电场,一般可以将电能直接接入陆上变电站,即一个风电场即属于一个变电区域。但是对于一个拥有近百台或几百台风机的大型海上风电场来说,建设一个甚至多个海上变电站是十分必要的。因此,就带来了海上变电站数量优化、选址以及风机机群的变电区域划分(将风机根据所要连接的海上变电站的不同进行分组)的问题。
结合目前变压器容量的考虑,一个大型海上风电场即使建设多个海上变电站,其数量也是非常有限的,可以采用枚举算法进行数量优化。
海上变电站选址与变电区域划分两者是相互影响与制约的。根据海上变电站选址而进行的风机机群变电区域划分,其结果即是将大型风电场划分成了若干区块,区块与区块之间相互区别,风机对每个海上变电站来说,从连接成本上表现出一定的亲疏关系,但各变电区块的归属在未划分之前具有一定的不确定性。且在进行变电区域划分时,地理位置相对聚集的风电机组同属于一个变电区域的可能性较大。这与聚类算法具有许多相似之处。本文采用模糊C均值FCM(fuzzy C-means)[9]算法进行变电区域划分。

式中:m为一个加权指数,m∈[1,∞);dij为第i个聚类中心(即海上变电站)与第j个数据点(即第j台风机)间的欧几里得距离,取dij=‖Oi-Xj‖,Xj为风机节点(j=1,2,…,NWT),Oi为群心(即第i个海上变电站的位置),Oi的更新计算公式为Oi(k+1)=;uij为数据隶属度,介于0~1之间,在第k次迭代中,如果∀j,r,drj(k)>0,则

如果∀j,r,drj(k)=0,则

当迭代至群心O的变化矩阵范数‖O(k+1)-O(k)‖小于给定的阈值时,迭代结束。
计算结果的n个聚类中心为海上变电站位置,而n个子集对应的风机节点分类即为风机集群的分区结果。
2.2 考虑规避区域的海底电缆连接拓扑可行解
每个变电区域内的风机经海底电缆相互连接后,接入该区域中的海上变电站。考虑到海底条件的限制,可能会对海底电缆敷设产生一定的制约,因此,海底电缆敷设需要考虑一定的规避区域。通过海底勘测获得的规避区域通常是有限并且明确的,可以作为输入的约束条件。在进行海上风电场集电系统优化时,为了保证优化结果的实际可操作性,可以事先形成海底电缆拓扑的可行解空间。
经过分析发现,风机偏向于与它周围较近的风机连接,并且考虑到工程实际的需要,海底电缆不允许出现交叉、大跨越等情况。本文采用Delaunay三角剖分算法[9]对风电场进行网格化处理从而获得风机之间的连接拓扑可行解。Delaunay三角剖分将点集形成的凸多边形剖分成一系列三角形,从而能够保证所有的边之间没有交叉。考虑到规避区域的存在,若生成的Delaunay三角网格中的某些边与规避区存在交叉关系的话,这样的边由于实际施工关系是无法利用的。为了解决该问题,本文对生成的Delaunay三角网格的每条边进行筛选,对于与规避区有交叉的边进行删除处理。规避区可以根据工程实测数据采用包围节点集描述。
根据数值模拟结果,基坑开挖卸载对隧道结构影响较大,近阶段隧道局部结构已经丧失继续承载的能力。为此,近接基坑区段的隧道套拱设计为钢筋混凝土结构形式。设计套拱结构为200 mm厚C30混凝土+120 mm格栅拱架+内侧单层钢筋网片结构。根据对隧道净空的调查结果,隧道套拱施作完成后,基本能够净宽1.3 m的使用要求。钢架采用4肢格栅钢架,纵向间距1.0 m/榀,相邻钢架之间采用直径20 mm的钢筋进行纵向连接,纵向连接筋环向间距0.5 m,内外双侧布置;钢筋网片网格间距150 mm×150 mm,钢筋直径6 mm。
以图2所示的12个节点为例,其中变形区域为规避区。采用Delaunay三角网格可生成图3所示路径,在此基础上,去除经过规避区的可行路径,则可以得到图4所示的可行解。该方法可以较好地解决海底电缆敷设的规避区域问题,能够避免出现海底电缆交叉,并进行海底电缆敷设路线的预处理。
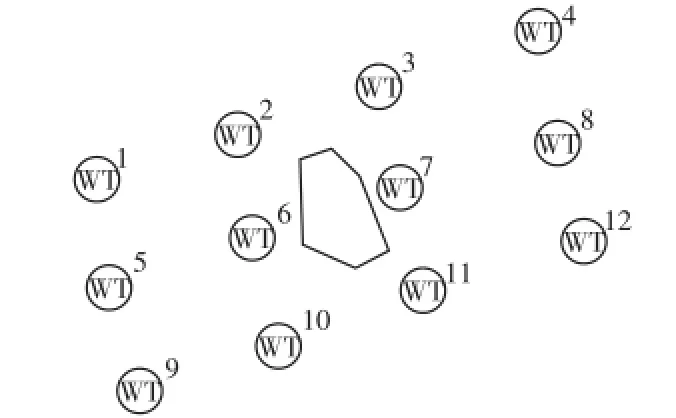
图2 12个风机节点及规避区域示意Fig.2 Schematic of 12 wind turbine nodes and the forbidden zone
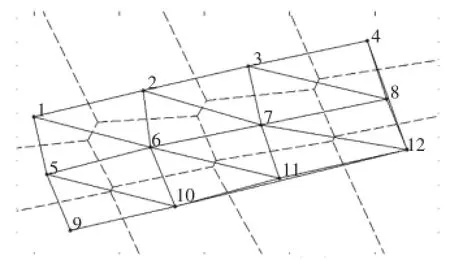
图3 Delaunay三角网格结果Fig.3 Result of Delaunay triangulation

图4 考虑规避区约束的可行网络拓扑Fig.4 Feasible network topology considering the forbidden zone
2.3 变电区域内风机群分组(串)算法
对于一个具有大量风机的海上风电场来说,即使通过第2.2节的方法构建了海底电缆拓扑连接的可行性方案,由于其中连接复杂,其可行解空间仍十分巨大。目前海上风电场内部风机通常以“串”形结构相互连接,且每串风机的数量大体相当。从可供选择的海底电缆载流量来看,每串风机的数量可以由最粗与最细的海底电缆与风机容量来确定,其值通常在5~20之间,可以考虑采用枚举法进行选优。因此,在每串风机数量给定的前提下,集电系统的拓扑连接问题便可以简化为对给定变电区域内的风机机群分组与组内风机之间的拓扑连接问题。
对于同一变电区域中的风机分组,即是将风机分“串”。“串”与“串”之间的风机由于海底电缆连接成本问题表现出一定的亲疏关系,且同样存在海底电缆不能交叉的约束。因此,从本质上看,风机分组与第2.1节中的风机变电区域划分并无本质的区别。不同的只是变电站分区是将风机群划分为相对松散的块状模式,如图5(a)所示,而风机的分组还需要保证每串风机均存在至变电站的通路,且不经过其他分组,如图5(b)所示。

图5 风机群的分区与分串聚类效果示意Fig.5 Schematic of partitioning and clustering of wind turbines
为了保证海底电缆之间没有交叉的问题,本文在第2.1节的聚类算法基础上进行改进,以实现节点如图5(b)所示的类似“扇形”的聚类效果。算法结构与第2.1节中的大致相同,计算方法如式(3)~式(5)所示,唯一的区别是这里重新定义了dij。dij定义为第j个风机节点到第i类聚类中心与由第2.1节方法确定的海上变电站节点的连线之间的距离,具体如图6所示。因此,若α<90∘,则dij= ||D sinα;若α>90∘,则dij=∞。该聚类方法本质上是将风机按线性结构聚集,从而保证风机各“串”之间不出现交叉的海底电缆接线。

图6 dij定义示意Fig.6 Schematic of definition of dij ij
2.4 风机“串”的拓扑寻优
“串”形连接的风机,由于每段海底电缆的载流量不同、拓扑结构不同导致的节点短路电流大小的差异都可能造成每段电缆的型号存在较大的差异,从而造成经济性的差异。也就是说,不同的风机“串”的拓扑结构对经济性成本有一定影响。考虑到大型风电场所需的海底电缆的数量相当可观,在满足相应技术要求的条件下可以通过寻求尽可能合理的拓扑方式以节约海底电缆的投资成本。
对于如图7(a)所示的某组风机间电缆连接的可行方案,为了找出其中最优的电缆拓扑,需要实现两个方面的要求:①连接是一棵“树”,以保证没有环路;②,其中n为包含风机和变电站的节点总数,Li与ci为第i段海底电缆的长度与价格。因此,风机“串”的连接优化问题可以视为是从一个如图7(a)所示的带权无向完全图中选择n-1条边并使这个图仍然连通(也即得到一个生成树),同时还要考虑使树的权最小。其本质即是图论中的最小生成树问题,因此,本文采用最著名的Prim算法进行求解[10]。
在上述基础上,完成所有海上变电站定容选址,并形成了风机之间的连接拓扑后就可按电气计算的方法进行海底电缆选型和校验,确定各电气设备的数量、容量及价格,最后按式(1)和式(2)计算得到整个海上风电场集电系统的总投资。在枚举的海上变电站数量及风机连接数量后,选定总投资最小的一组解为最优解。

图7 某“串”风机电缆拓扑示意Fig.7 Topological schematic of a string of wind turbines and cables
3 算例分析
以某规划中大型海上风电场为算例。该海上风电场共规划布置风机582台,单机容量2 MW,风机间距大于600 m,其分布如图8所示。

图8 某大型海上风电场风机布置Fig.8 Arrangement of wind turbines in large-scale offshore wind farm
按图1的总体流程思路进行优化,风电场总容量为1 164 MW,采用220 kV输电电压,根据220 kV变压器标准容量,变电站按双变压器配置计算,初步确定建设3~10个海上变电站。
根据风机1.5 MW的容量可以得到风机箱变出口35 kV侧额定电流为33 A,按35 kV可选截面的海底电缆额定载流量可以确定每串风机数量为7~18台。
1)变电区域划分
采用第2.1节中的FCM算法对该海上风电场风机进行变电区域划分,可以枚举分区数量分别为3~10时的分区结果,图9为4个海上变电站时的分区与选址结果。
2)拓扑连接优化
根据第2.2~2.4节的内容,在变电区域划分的基础上,生成每个变电区域中风机间连接拓扑的可行性方案,然后采用改进FCM算法进行风机分组,并采用Prim算法获得风机间的拓扑连接方案。图10是6个海上变电站时集电系统的拓扑优化结果。

图9 4个海上变电站时的分区结果与变电站选址Fig.9 Partitions and locations of 4 offshore substations

图10 分6区时的拓扑优化结果Fig.10 Result of topological optimization for wind turbines with 6 offshore substations
3)经济性比较
海上变电站数量不同时,整个风电场电气设备投资存在较大差异。本文通过枚举算法进行寻优,结果如图11所示。该海上风电场采用6个海上变电站时经济性最优。
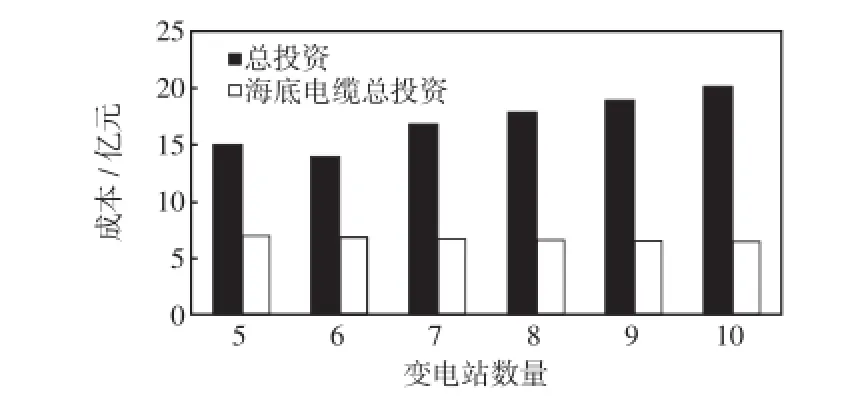
图11 不同海上变电站经济性比较Fig.11 Comparison of cost with different offshore substations
4 结论
(1)大型海上风电场采用海底电缆将风机、海上变电站相互连接,连接的拓扑形式对集电系统经济性具有较大影响。本文根据海上风电场集电系统固有的特点,将大型海上风电场集电系统优化问题整理为变电区域划分、风机拓扑可行性方案求解、风机“串”的划分以及风机间优化连接4个问题。
(2)本文结合海上风电场集电系统特性及图论理论,分别采用FCM算法、Delaunay三角剖分算法、改进FCM算法以及Prim算法进行上述4个问题的求解。实际算例说明,该算法是有效的。
参考文献:
[1]Global Wind Energy Council.Global wind statistics 2014 [EB/OL].http://www.gwec.net/global-figures/graphs,2015.
[2]蒋卫龙,邓文浪,郭有贵,等(Jiang Weilong,Deng Wen⁃lang,Guo Yougui,et al).基于RMC的海上风电-HVDC系统功率协调控制(Coordinated control of power for di⁃rect-driven offshore wind power generation-HVDC system based on RMC)[J].电力系统及其自动化学报(Proceed⁃ings of the CSU-EPSA),2015,10(27):1-8.
[3]王建东,李国杰(Wang Jiandong,Li Guojie).海上风电场内部电气系统布局经济性对比(Medium term unit commitment based on outer approximation method)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(11):99-103.
[4]Jin Yang,O’Reilly J,Fletcher J E.Redundancy analysis of offshore wind farm collection and transmission systems [C]//International Conference on Sustainable Power Gener⁃ation and Supply.Nanjing,China,2009.
[5]黄玲玲,符杨,郭晓明(Huang Linging,Fu Yang,Guo Xiaoming).大型海上风电场电气接线方案优化研究(Research on optimization of electrical connection scheme for a large offshore wind farm)[J].电网技术(Power Sys⁃tem Technology),2008,32(8):77-81.
[6]王锡凡,王碧阳,王秀丽,等(Wang Xifan,Wang Biyang,Wang Xiuli,et al).面向低碳的海上风电系统优化规划研究(Study of optimal planning methods for offshore wind oower systems oriented low-carbon)[J].电力系统自动化(Automation of Electric Power Systems),2014,38 (17):4-14.
[7]郑小霞,张秦墉,符杨,等(Zheng Xiaoxia,Zhang Qin⁃yong,Fu Yang,et al).面向海上风电机组运行维护的Petri网模型(Operation and maintenance model for off⁃shore wind turbine based on Petri nets)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26 (6):10-13.
[8]Dicorato M,Forte G,Pisani M,et al.Guidelines for assess⁃ment of investment cost for offshore wind generation[J].Renewable Energy,2011,36(8):2043-2051.
[9]龚劬.图论与网络最优化算法[M].重庆:重庆大学出版社,2009.
[10]王海英,黄强,李传涛,等.图论算法及其MATLAB实现[M].北京:北京航空航天大学出版社,2010.
樊 潇(1975—),女,硕士,高级工程师,研究方向为发电厂及新能源电气设计。Email:fanxiao@sdepci.com
卢永魁(1984—),男,硕士,工程师,研究方向为发电厂及新能源电气设计。Email:luyongkui@sdepci.com
黄玲玲(1982—),女,通信作者,硕士,副教授,研究方向为海上风力发电及电力系统继电保护等。Email:lingling⁃huang82@126.com
中图分类号:TM614
文献标志码:A
文章编号:1003-8930(2016)07-0051-06
DOI:10.3969/j.issn.1003-8930.2016.07.010
作者简介:
收稿日期:2014-10-11;修回日期:2015-12-26
基金项目:上海绿色能源并网工程技术研究中心资助项目(13DZ2251900);上海市科委科技创新资助项目(14DZ1200905)
Network Topology Optimization of Electrical Collection System of Large-scale Offshore Wind Farm
FAN Xiao1,LU Yongkui1,HUANG Lingling2,WEI Shurong2
(1.Shandong Electric Power Engineering Consulting Institute Corp.,Ltd,Jinan 250013,China;2.College of Power and Automation,Shanghai University of Electric Power,Shanghai 200090,China)
Abstract:The cost of large-scale offshore wind farm is very high due to the adoption of expensive offshore marine ca⁃bles and other offshore facilities.In this paper,an economic analysis model of electrical collection system is estab⁃lished.To analyze the interactive relationships among different factors,this paper decomposes the economic problem in⁃to two parts by using the top-down approach,i.e.,optimization at offshore substation level and optimization at wind tur⁃bines level.To improve the practicability of the proposed method,the requirement of non-intersection for marine cables and avoidance region resulting from particular seabed conditions are also considered.Graph theory is introduced to solve the problem,and an example shows that the proposed method is effective.
Key words:large-scale offshore wind farm;electrical collection system;graph theory;fuzzy C-means algorithm
