德州能见度与PM2.5、PM10和相对湿度的关系

2016-08-03高雷娜朱保美

海洋气象学报 2016年2期

关键词：德州能见度气溶胶

张　琳，高雷娜，朱保美

（1. 德州市气象局，山东　德州　253000；2. 齐河县气象局，山东　齐河　251100）

德州能见度与PM2.5、PM10和相对湿度的关系

张琳1，高雷娜1，朱保美2

（1. 德州市气象局，山东德州253000；2. 齐河县气象局，山东齐河251100）

为研究德州大气能见度与水汽和气溶胶的关系，利用2013年逐小时能见度、相对湿度、PM2.5和PM10浓度资料，对三者与能见度的关系进行分析。结果表明：能见度与相对湿度的线性相关最好，与PM2.5浓度的相关性次之；随着相对湿度、PM2.5和PM10浓度的增加，能见度明显降低。大气能见度与相对湿度、PM2.5和PM10浓度非线性相关系数明显高于线性相关系数。利用PM2.5和PM10浓度和相对湿度数据计算得到了非线性大气能见度拟合公式，经验证，该公式能较好地模拟德州大气能见度。

能见度；PM2.5；PM10；相对湿度；非线性拟合

引言

大气能见度是表征大气透明度的物理量，与百姓生活息息相关，而且可以反映当地的空气质量。德州市位于山东省北部，与河北交界。2006年以来，雾-霾天数明显增多，雾-霾天气出现时，不仅空气质量较差，对人体健康不利，而且由于能见度下降，常常造成交通事故。因此大气能见度的研究受到广大气象和环境工作者的广泛关注。国外一些学者发现大气能见度与大气气溶胶浓度密切相关［1-2］。马雁军［3-4］等将辽宁部分城市的大气能见度与影响因子进行分析，发现能见度与相对湿度和PM10呈明显负相关。宋宇［5］等讨论了北京市能见度下降与气溶胶浓度的关系，得出北京气溶胶粒子散射消光占总消光70%～80%。宋明等［6］利用天津相对湿度、PM10和PM2.5数据对当地大气能见度进行多元非线性拟合，并以此来推算大气能见度。崔宜少［7］分析了威海监测站的PM2.5平均值与风向、风速及天气形势的相关性。有些文章还对空气污染物时序特征与气象条件的关系进行了研究［8-10］。此文旨在研究德州大气中气溶胶浓度以及水汽与能见度下降的关系，在借鉴前人研究成果的基础上，采用非线性方法将PM10 和PM2.5浓度以及相对湿度与能见度的关系进行量化分析，并在此基础上建立多元非线性拟合方程，为大气能见度的业务预报提供参考依据。

1　资料来源和处理

大气气溶胶浓度数据来自德州市环保局监测站2013年1—12月全年逐小时资料。在使用前，先剔除数值为0或者999.9的资料。其次剔除由于监测设备异常时出现的 PM2.5浓度大于PM10浓度的资料。

气象资料来源于德州气象观测站，站点位于德州市开发区长河公园内。德州气象观测站CAWS737-V型能见度自动观测仪量程为0～20km，采集频率达到了1次/min。气象观测执行国家相关标准，所有设备进行过校准。所有资料均进行了严格的质量控制。所有数据统一处理成小时平均值。当出现明显降水时，能见度仪的观测值会出现明显降低，因此必须将出现降水时的资料剔除。

经过资料处理，最终所用数据均为较精细的小时平均资料，共计 6424组，完全可以满足分析大气能见度逐时变化、日变化规律及受各种气象因素实时影响的研究要求。

2　大气能见度与相对湿度及PM10和PM2.5的逐月变化

选取 2013年德州逐月大气能见度与同期相对湿度、PM2.5和PM10资料进行对比分析。由图1a可知，德州能见度和相对湿度逐月度变化较为明显。能见度在3—6月、11月较高，1—2月、7月、12月较低；相对湿度在1—2月、7—8月较高，3—6、11—12月较低，相对湿度与能见度呈现负相关关系。由图1b可知，PM2.5、PM10的月变化规律较为一致，在1—2月、7月、12月数值较高，其他月份相对较低，与能见度同样呈现出负相关关系。

3　大气能见度与相对湿度及PM10和PM2.5的线性关系

表1　大气能见度与相对湿度、PM2.5和PM10及PM10 与PM2.5浓度差线性相关系数

由表 1可知，大气能见度与相对湿度的相关系数最高，达到了-0.647，在0.001水平上显著相关；与PM2.5的相关系数较高，为-0.612，同样在0.001水平上显著相关。说明随相对湿度和PM2.5的升高，大气能见度明显下降。相对湿度增加，能见度下降主要是由于随相对湿度增高，核模态大气气溶胶粒子（粒径介于 0.005～0.050μm）吸湿增长，逐步转化为积聚模态（粒径介于 0.05～2.00μm）。大粒子的散射效率明显高于小粒子，从而加剧了对可见光的散射，使大气能见度下降。大气能见度与PM10和PM2.5差值的相关系数为-0.180，说明粒径介于2.5～10.0μm的大气气溶胶粒子较PM2.5对大气能见度影响小。虽然这部分粒子散射效率高于小粒子，但其浓度远低于小于2.5μm的气溶胶粒子，据统计，德州 PM2.5占到了PM10总量的67%，所以粒径介于2.5～10.0μm的粒子对太阳光的散射作用小于PM2.5。

4　大气能见度与相对湿度、PM2.5和 PM10的非线性关系

4.1大气能见度与PM2.5和PM10的非线性关系

实际情况下，能见度与PM2.5，PM10不呈现出简单的线性关系，由散点图（图 2）中，明显可以看出，其关系呈现较为复杂的非线性关系。

由以上分析可知，大气能见度受空气中的水汽、PM2.5、PM10浓度影响明显，为验证大气能见度与相对湿度、PM2.5、PM10浓度的关系，将大气能见度与相对湿度、PM2.5浓度、PM10浓度及PM10与PM2.5浓度差分别进行线性拟合（表1）。

图2　能见度与PM2.5（a）和PM10（b）浓度分布散点图

为验证大气能见度与相对湿度、大气气溶胶的关系，为业务化预报提供依据，宋明等［6］将相对湿度分为＜19%、20%～29%、30%～39%、40%～49%、50%～59%、60%～69%、70%～79%、80%～89%、＞90%共9个等级，分别对能见度与PM2.5和PM10浓度进行非线性拟合。很多科研工作者认为大气颗粒物与大气能见度呈负指数关系［11］。SPSS为IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品及相关服务的总称，它和SAS、BMDP并称为国际上最有影响的三大统计软件。《SPSS统计分析高级教程》［12］一书中指出，非线性回归的通用模型可以采用迭代法对各种复杂曲线模型进行拟合，按照书中教程可建立如下拟合方程：

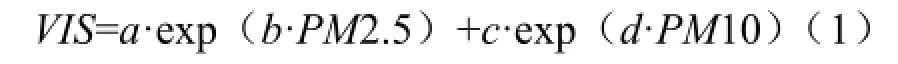
式（1）中，VIS为能见度（km），PM2.5、PM10为浓度（mg·m-3），a、b、c、d为系数。拟合方程参数如表2。

由表2中发现，当相对湿度大于80%时，拟合结果与实况值相关系数的平方（R2）较相对湿度比较小时有明显降低。这也说明当相对湿度大于80%时，随着相对湿度的增大，能见度受PM2.5 和PM10浓度的影响有所减小。气溶胶中硫酸盐、硝酸盐等潮解湿度一般在80%左右，当相对湿度超过潮解湿度时，会造成盐粒子粒径随相对湿度增加而迅速增加，加剧对可见光的散射，相对湿度对能见度的影响明显增加，受PM2.5和PM10浓度的影响则相对减小，与之前的分析一致。

表2　不同湿度条件下，能见度与PM2.5和PM10浓度拟合参数表

4.2大气能见度与相对湿度的非线性关系

图3中发现能见度与相对湿度的分布非常混乱，似乎不存在明显的相关性，但由前文分析结论，相对湿度与能见度呈现非常明显的负相关，图2之所以非常混乱，是因为未考虑气溶胶浓度的影响。下面分析在PM2.5和PM10浓度变化较小（小于等于 0.005mg·m-3）的情况下，能见度与相对湿度的关系。

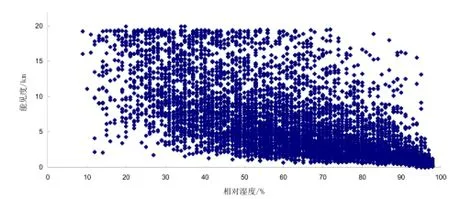
图3　能见度与相对湿度分布散点图

由于 PM2.5，PM10数据众多，因此采用6个分别代表低、中、高浓度的数据集进行分析，样本总量达1188个，使用SPSS软件进行分析，发现能见度与相对湿度的3次方多项式有较好的拟合关系，其方程如下：

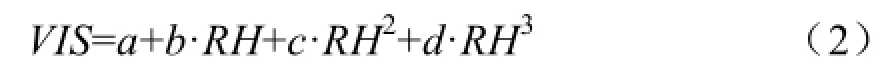
式（2）中，VIS为能见度（km），RH为相对湿度（0～100%），a、b、c、d为系数。拟合方程参数如表3。

由表3可知，相对湿度与能见度拟合的方程整体来看效果还是不错，可以使用方程2来模拟能见度与相对湿度的关系。但是随着PM10浓度增加，R2明显减小，这可能是与非吸湿性粒子的增多有关系，使能见度与相对湿度的相关性下降。

表3　不同PM2.5，PM10浓度下，能见度与相对湿度拟合参数表

5　大气能见度多元非线性拟合及验证

5.1大气能见度多元非线性拟合公式

综合以上结果，仅考虑PM2.5、PM10和相对湿度对大气能见度的影响，其他因素暂不考虑，利用SPSS软件对大气能见度进行多元非线性拟合。拟合公式：

式（3）中VIS1为能见度（km），PM2.5、PM10为浓度（mg·m-3），RH为相对湿度（%），a～g为系数。最终拟合参数如表4所示。

表4　大气能见度与PM2.5和PM10浓度及相对湿度非线性拟合参数

经过拟合之后的能见度在与实况能见度进行对比时发现，实际能见度与式（3）拟合结果仍呈现 2次多项式的关系，因此在式（3）的基础上，再次进行修正，最终得到拟合公式。

式（4）中，VIS为最终拟合能见度，VIS1为式（3）得出的拟合能见度。拟合结果偶尔会出现小于0的情况，这与实际明显不符，因此拟合结果小于0时，强制其为0。

5.2大气能见度多元非线性拟合公式验证

为了验证上节得出的能见度拟合公式，选取2013年4月和12月小时数据进行验证。由于雾、霾都出现在低能见度时，因此对拟合能见度小于3km（霾预警信号发布标准之一）的数据进行了单独分析，结果如表5所示。

表5　2013年4月和12月验证结果

图4为拟合能见度与实测能见度的散点图，4月（图4a）和12月（图4b）的拟合值与实测值吻合均较好，相关系数达到了0.93（通过显著性水平0.001检验），平均绝对误差在1.5km左右，尤其是在能见度小于3km时，平均绝对误差更是只有0.38km和0.59km（表5）。以上结果说明可以使用式（3）和式（4）通过PM10、PM2.5浓度和相对湿度对大气能见度进行模拟。