考虑节点自修复能力的C2关系网络毁伤特性研究*

任清辉，张东戈

（解放军理工大学指挥信息系统学院，南京　210007）

考虑节点自修复能力的C2关系网络毁伤特性研究*

任清辉，张东戈

（解放军理工大学指挥信息系统学院，南京210007）

摘要：针对指挥控制关系网络受到攻击时节点及网络毁伤程度的量化评价问题，首先形式化定义了攻击强度和节点自修复能力函数，在此基础上，分别给出了网络中节点无自修复能力和自修复能力随时间变化时的节点毁伤模型。最后通过仿真计算，得到了节点的失效过程描述以及随机攻击和选择性攻击两种不同攻击目标选择方式下网络效率随攻击时间的变化关系。

关键词：攻击强度，自修复能力，毁伤模型，网络效率

0　引言

指挥控制（Command and Control）关系网络，即C2关系网络是现代战场上的攻防热点。采用科学方法定量化地研究C2关系网络的毁伤特性，在C2组织设计、节点的针对性防护等诸多领域都具有重要价值，同时，它也是网络抗毁性研究中的一个重要研究内容之一［1］。

系统复杂性理论为C2关系网络抗毁性研究提供了有效方法，它将C2组织结构中的作战实体抽象为节点，节点之间如果存在信息流联系，则抽象为具有连接关系的边，进而，在抽象出的网络中利用复杂网络的各种特性分析C2组织结构的性质，并预测系统的行为特性［2-3］。Albert等［4］最早对复杂网络抗毁性进行了研究并指出“在随机攻击下，无标度网络相对随机网络具有更强的抗毁性，但是无标度网络面对选择性攻击却显得异常脆弱”。在Albert等人研究的基础上，Xiong J S等［5］根据核度理论、Wang W等［6］基于随机游走介入模型（RB）、He S J等［7］提出了循环介入策略分别对Albert的研究进行了拓展，并证明了网络抗毁性的可计算性。这些研究为C2关系网络抗毁性的量化研究提供了有效方法。然而研究中也发现，直接移除节点的攻击方式与C2关系网络遭受攻击的实际情况不符。为解决这一问题，田旭光等［8］提出了一种网络动态抗毁性的度量方法，从打击效果的角度对指挥控制系统的动态抗毁性进行了研究，得到了更符合指挥控制系统的网络动态抗毁性特征。不过，在田旭光的研究中，没有考虑节点本身效能的下降过程。从以上研究中可以看到，当前研究主要是从攻击目标选择、网络受到攻击后损伤大小的角度对网络的抗毁性进行了研究，但是对于节点的毁伤过程以及由此引发的网络性能的变化过程依然缺少足够的定量化描述。

为更进一步研究C2关系网络遭受攻击后的毁伤特性，本文通过引入节点自修复能力和攻击强度函数，将对C2节点状态的定性描述转化为其失效过程的定量描述，从而建立更符合一般化要求的节点毁伤模型，进而在随机攻击和选择性攻击下，仿真计算网络受到攻击后网络效率随攻击时间的变化过程。

1　节点毁伤特性分析

从攻击效果的角度来观察，人们将C2关系网络所受到的攻击分为毁伤性攻击和非毁伤性攻击，其中，毁伤性攻击是攻击强度足够大的非毁伤性攻击的极端情况。为了对网络节点遭受非毁伤性攻击时的毁伤特性进行分析，将节点的毁伤过程转化为其效能的下降过程，并在此基础上研究C2关系网络的毁伤特性。

在本研究中，将指挥控制系统的拓扑结构联系抽象为复杂网络模型G=（V，E）［9］，其中V和E分别是网络中节点的集合和边的集合，设定正整数N=是网络的节点个数。网络节点间的邻接矩阵设为A=aij，aij=1表示节点i和节点（ji≠j）之间具有直接连接关系，否则设定aij=0。

1.1节点毁伤过程影响因素

为量化描述节点任一时刻的工作状态，记节点完好率为H（t），它表示t时刻某一节点的可用效能占其初始最大完好效能的比例，由此在t时刻节点的失效率可表示为G（t）=1-H（t），G（t）=1表示节点完全失效。假设初始时网络中的所有节点效能可以达到最大完好，由此t=0时有G（0）=0。进而，可经由G（t）的值对网络中任一节点在t时刻的毁伤状态进行评价。

C2节点受到攻击时，其毁伤过程主要受以下两个因素的影响：①攻击方的攻击强度大小；②节点自修复能力的强弱。为研究节点毁伤过程，首先要对这两个影响因素进行形式化描述。

定义1记ω是节点受到攻击的攻击强度，它表示不考虑自修复能力的情况下，攻击目标节点在单位时间内效能下降的百分比。

在实际战场环境中，攻击方的攻击强度ω是一个与战场环境因素、攻击方实施攻击的能力以及目标节点重要程度等有关的量，但是攻击时多半会采用一招制敌的战术，因此，多半会取一个较大的固定可用值。为简化计算，作出如下假设：

假设1网络中任一节点受到攻击时的攻击强度大小相同，为ω。

定义2记v是节点的自修复速率，它表示不考虑节点所受攻击强度的情况下，单位时间内修复自身效能的百分比，节点的自修复速率越大，则其自修复能力越强。

由于在实际作战中，重要性高的节点往往会受到更多的保护，因此，就节点重要性我们有如下假设：

假设2假设在C2关系网络中，节点的重要性越大，那么该节点在修复过程中的平均自修复速率vi越大，并且设其表达式为：

这里采用与节点直接相连的个体数，即度（数）的大小，来评价节点重要性［10］，认定度数越大，节点越重要，可得节点i的重要性的值。式（1）中，是网络中共计N个节点的重要性的平均值；v0是一个常数值，它用来表示重要性为S的节点的平均自修复速率。显然，若仅以vi作为节点受到攻击时自修复能力的评价标准，只能得到节点毁伤过程的粗略描述，而无法反映节点毁伤过程的一般特性。

分析C2节点的自修复过程，我们发现：在任一时刻t，节点的自修复速率v（t）的大小与其当前完好率H（t）以及是否迫切需要修复的紧急程度有关。通常失效率G（t）的值越大，意味着紧急程度越高，由此可以用失效率G（t）来代表紧急程度。也就是说，当节点完好率较低时，意味着修复该节点的紧急性程度要求较高，但由于节点的毁伤程度较大，修复难度也就较大，这使得自修复速率较小，此时节点的自修复速率随着完好率的增长而逐渐变大；而当完好率较高时，意味着修复该节点的紧急程度会低，节点上的资源会更多地用在使命任务的完成上面，这使得此时的节点自修复速率虽然较大，但其值随着完好率的增长而逐渐变小。当节点数目足够大的时候，上述统计特征规律就会比较明显。

通过以上分析可知，v（t）是一个关于H（t）和G（t）的函数，这里设定它与二者均成正比例关系，即有：

其中，c是与节点的重要程度等因素有关的一个比例系数。分析式（2）求极值可得，当H（t）=0.5时，有节点自修复速率的最大值vmax=14c，将c代入可得节点自修复速率表达式（2）有：

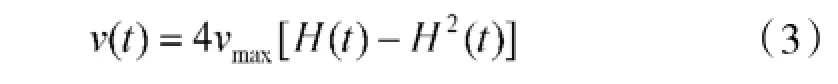
分别考虑节点自修复速率以平均值v=vi以及随时间变化v=v（t）两种情况，得到节点自修复速率随其完好率的变化关系曲线如图1所示。

图1　节点自修复速率—完好率变化关系图

从图1（a）可以看出，对任一节点i，如果设定v= vi，节点自修复速率是一个与节点完好率状态无关的常数vi，无法反映节点在各毁伤状态时自修复能力的差异性；而设定v=v（t）时，其变化曲线如图1 （b）所示，节点自修复速率在各完好率状态下均不相同，可以反映节点自修复过程的一般规律。

根据假设2，节点i在自修复过程中，其自修复速率的平均值为vi，则当该节点自修复速率随时间变化时，自修复速率的平均值也应该满足v（t）=vi。设Tr是节点的总修复时间，由于v（t）是t∈［0，Tr］上的连续函数，所以v（t）等于v（t）在［0，Tr］区间上的定积分除以该区间长度Tr，进而有如下关系式：

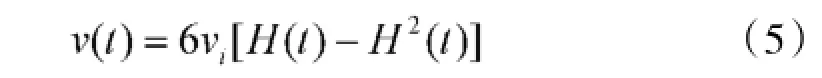
结合攻击方攻击强度及节点自修复速率变化情况，可以对C2网络中节点的毁伤过程进行建模研究。

1.2节点毁伤特性建模

在非毁伤性攻击下，可以通过一段时间内节点失效率增加的多少来表示这段时间内节点的平均毁伤速率。Δt时间内节点的平均毁伤速率可表示为：，当Δt足够小时，该式的计算结果即是t时刻节点毁伤的瞬时速率。又由于节点的失效过程随时间的变化是一个连续过程，所以G（t）在定义域t∈［0，Tlast］内可导，其中Tlast是节点失效时间，进而得到节点在t时刻的毁伤速率：

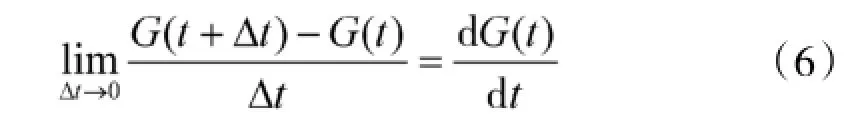
式中，dG（t）/dt是失效率G（t）在t时刻的导数，在这里表示节点在t时刻的毁伤速率。

通过对节点毁伤速率的计算，可以对各种自修复速率取值下的节点毁伤过程进行研究。对任一节点i，将其毁伤影响过程从简单到复杂分为以下2种情况：

1）不考虑节点自修复能力

此时是节点失效过程的最简化情况，节点毁伤速率为：

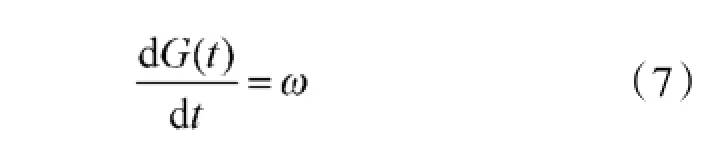
解微分方程得G（t）=ωt+C，其中C是常数，由于设定开始时节点最大完好，即G（0）=0，所以可得C=0，G（t）=ωt。从而可得：在不考虑节点自修复能力情况下，节点的失效时间仅与攻击强度有关，并在t=1/ω时刻节点达到完全失效。

2）节点自修复能力随时间变化

设定节点自修复速率为v（t），由于G（t）=1-H（t），代入式（5）可得：

此时节点毁伤速率为：

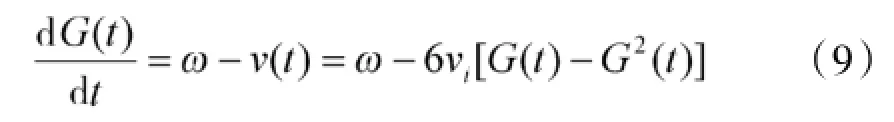
2　C2关系网络毁伤特性仿真研究

从第1节的计算结果可以看出，对网络中的不同节点，即使它们受到的攻击强度大小相同，但由于自修复能力的强弱差异，其失效过程也各不相同，而节点的失效又必然会导致网络性能的下降，本节中依据复杂网络中的BA模型［11］构造节点个数N=100，度分布p（k）∝k-3［12］的指挥控制关系无尺度网络图，在此基础上仿真计算研究节点的失效过程以及C2关系网络的毁伤影响过程。

图2　C2关系网络拓扑结构示意图

2.1节点失效过程的仿真计算

由于仅当攻击强度大于节点自修复速率时其完好率才会下降，因此，研究中假设节点受到的攻击强度总是大于其最大自修复速率，即设定ω＞3/2max （vi），其中max（vi）是网络中所有节点中平均自修复速率的最大值，进而不等式可表示为：

式（10）中，max（Si）是网络中所有节点的重要性的最大值。按照仿真参数设定计算可得，网络中max（Si）= 20、S=5.34，当设定ω=0.2时，由满足不等式（10）计算可得v0＜0.068 9。据此，研究中取v0=0.065。

根据上述设定和计算，以重要性Si=13的节点为例，可以得到节点无自修复能力v=0以及自修复速率随时间变化v=v（t）两种情况下，节点失效率随时间的变化关系，如图3所示。

图3　节点失效率随时间变化曲线图

从图3中可以看到，v=0时的节点完全失效时间为t=5时刻，而当v=v（t）时，其完全失效时间则为t=12.411 7，远大于v=0时的情况。此外，当v=v（t）时的节点失效率随时间t的变化是一条曲线，曲线的斜率开始时逐渐减小，再逐渐增大，并且拐点在t=3.875处，此时曲线斜率最小。由此可得：

结论1：节点的自修复能力能够极大地提高其承受攻击的能力，并且节点的毁伤速率在开始受到攻击的一段时间内由快逐渐变慢直至降到最小值，然后再逐渐变快。即毁伤达到一定程度的时候，毁伤状况会呈现出加速发展的情况。

2.2C2关系网络毁伤过程仿真

节点因受到攻击而失效，最终都会反映在整个C2关系网络性能的下降上，由于在指挥控制系统中，指挥控制信息的传输效率在一定程度上代表了系统的效率，因此，可以用信息传输的网络效率［13］作为C2关系网络性能的评价指标，以下简称为网络效率，其表达式为：

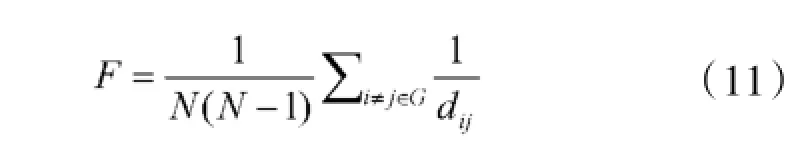
式（11）中，dij是网络中任意两个不同节点之间的最短路径长度。

在计算网络效率的基础上，可以对C2关系网络受到攻击后的毁伤状态进行仿真研究，并作出如下攻击想定：

想定1假设攻击方同一时刻只对一个节点进行攻击，并且攻击方针对某一节点的攻击会持续到该节点完全失效后才选择下一个节点进行攻击。

想定2攻击方的攻击目标节点选择方式分为随机攻击和选择性攻击［14］两种，随机攻击即是随机的选择网络中的节点作为攻击目标，选择性攻击则会按照网络中节点重要性的大小顺序依次进行攻击。

在以上攻击想定的基础上，将整个仿真研究过程分为以下两种情况：

2.2.1不同攻击目标节点选择方式

针对图2所示无尺度型指挥控制关系网络，设定仿真时间t=100、攻击方式分别为随机攻击和选择性攻击的情况下，仿真得到节点无自修复能力v=0以及自修复速率随时间变化v=v（t）时网络效率随时间的变化关系，如下页图4所示。

从图4可以看到，t=0时刻网络处于初始状态，此时网络效率为F=0.197 8，随着攻击时间逐渐变长，网络效率呈下降趋势。当v=0时，两种攻击方式均渐次有20个节点失效，而当v=v（t）时则分别有14个和11个节点失效，由此导致v=v（t）时的网络效率下降速率均比v=0时的慢。需要说明的是，由于我们假设节点在未完全失效时依然能正常工作，使得节点受到攻击但未失效时，网络效率处于不变状态，所以图4中为阶梯形曲线。

图4　不同攻击方式下网络效率随时间变化曲线图

结论2无论采取哪种攻击目标节点选择方式，节点的自修复特性都可以有效减少相同时间内完全失效节点的数量，进而减缓网络受到攻击后的毁伤过程。

2.2.2不同节点自修复能力取值情况

设定仿真时间t=100、节点无自修复能力v=0以及自修复速率随时间变化v=v（t）的情况下，随机攻击和选择性攻击下的网络效率随时间的变化关系，如图5所示。

图5　不同修复能力下网络效率随时间变化曲线图

从图5中可以看到，当v=0时，随机攻击情况下的网络效率下降的速率小于选择性攻击时网络效率的下降速率，这与Albert等［4］的结论相同，但当v=v（t）时，随机攻击情况下网络效率的下降速率虽然小于选择性攻击时网络效率的下降速率，但二者差距不大。由此可得：

结论3对重要节点的选择性攻击可以取得更大的攻击效果，但有针对性地加强高重要性节点的自修复能力，可以极大地降低网络毁伤速率，使得随机攻击和选择性攻击的攻击效果差别不大。

3　结论

C2关系网络遭受攻击时，节点及网络的毁伤过程与攻击方特性以及C2关系网络自身特性密切相关。本文综合考虑了攻击强度、节点的重要性以及自修复能力等指标，相对于传统的研究方式更具有一般性，因此，可应用到C2关系网络抗毁性的一般性研究中。文中模型进行了一定程度的简化，未来还可以提出更加符合C2关系网络特性的节点重要性计算方法，以及节点效能下降对网络性能的影响等。

参考文献：

［1］段谟意.网络抗毁性及其评价指标研究［J］.小型微型计算机系统，2013，34（11）：2553-2557.

［2］马秀丽，孙可心，王红霞.基于复杂网络理论的C2组织网络拓扑结构研究［J］.火力与指挥控制，2010，35（2）：69-71.

［3］胡晓峰.战争复杂性与复杂体系仿真问题［J］.军事运筹与系统工程，2010，24（3）：27-34.

［4］ALBERT R，JEONG H，BARABASI A-L.Error and attack tolerance of complex networks［J］.Nature，2000（406）：378-382.

［5］XIONG J S.Invulnerability analysis of networked information system topologies based on core&coritivity theory［J］. Telecommunication Engineering，2013，53（4）：467-469.

［6］WANG W，HU B，DI P.Optimization of network invulnerability to cascading failure based on random-walk betweenness model［J］.IEEE，2011（1）：231-234.

［7］HE S J.A measure method for network invulnerability based on improved albert algorithm［J］.IEEE，2011：812-815.

［8］田旭光，朱元昌，邸彦强.指挥控制系统网络动态抗毁性［J］.火力与指挥控制，2012，37（6）：88-92.

［9］周道安，张东戈，常树春.C2组织指挥控制关系的形式化描述［J］.指挥控制与仿真，2009，30（4）：13-17.

［10］刘建国，任卓明，郭强，等.复杂网络中节点重要性排序的研究进展［J］.物理学报，2013，62（17）：178901-9.

［11］ANN A.The structure and function of complex networks［J］. Society for Industrial and Applied Mathematic Review，2003，45（2）：167-256.

［12］陶九阳，张东戈，赵普山.适应性指挥控制关系网的度分布［J］.系统工程理论与实践，2012，32（8）：1808-1813.

［13］TRAJANOVSKI S，HERNANDEZ J M，WINTERBACH W，et al.Robustness envelopes of networks［J］.Journal of Complex Networks，2013，1（1）：44-62.

［14］胡斌，黎放.多种攻击策略下无标度网络修复策略［J］.系统工程与电子技术，2010，32（1）：86-89.

中图分类号：N94

文献标识码：A

文章编号：1002-0640（2016）04-0030-05

收稿日期：2015-03-26修回日期：2015-04-15

*基金项目：国家自然科学基金（61174198）；全军军事学研究生基金资助项目（2011JY002-163）

作者简介：任清辉（1991-），男，黑龙江佳木斯人，硕士研究生。研究方向：指控系统与军事系统运筹分析。

Research on Mutilate Characteristics of C2 Network Considering Nodes'Self-healing Ability

REN Qing-hui，ZHANG Dong-ge
（College of Command Information Systems，PLA University of Science and Technology，Nanjing 210007，China）

Abstract：This paper quantitatively evaluate the damage degree of command and control relationship network when being attacked.Firstly，the attack strength and self-healing ability function of nodes in the network are defined.And then，two mutilate models are built considering nodes without self-healing ability and nodes whose self-healing ability is changing over time.Finally，the failure process of the nodes is simulated and simulate the network efficiency is analyzed under random attack and targeted attack.

Key words：attack strength，self-healing ability，mutilate models，network efficiency