新二维离散超混沌映射及其在图像加密的应用
2016-08-02崔明章王光义任国瑞靳培培
崔明章,王光义,任国瑞,靳培培
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
新二维离散超混沌映射及其在图像加密的应用
崔明章,王光义,任国瑞,靳培培
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
摘要:在分析logistic映射和cubic映射的基础上,针对一维映射混沌区间窄、映射函数简单的综合考量,提出了一种新的超混沌二维离散映射.该映射系统参数混沌区间大于logistic映射和cubic映射,映射值域也同样大于前二者,同时存在2个正的Laypunov指数的超混沌现象.迭代运算受计算机精度影响方面也低于一维映射.对其产生的二值伪随机序列进行了NIST标准测试,其随机性明显好于logistic和cubic映射.最后提出一个基于该二维映射的图像灰度加密算法,相比logistic和henon加密增大了密钥空间、降低了映射迭代的时间复杂度.
关键词:二维离散;伪随机;超混沌;图像加密
0引言
近年来,混沌系统的初值敏感及不可预测性被广泛应用于信息加密和保密通信领域.在对信息加密要求愈加严格的背景下,如何产生性能更加良好的混沌系统逐步发展成为热门的研究领域[1-6].混沌学包含离散混沌和连续混沌两种.连续混沌系统结构更为复杂,密钥空间大,然而从应用的角度来看,信息加密往往都是数字化的,连续混沌系统虽然结构复杂,但其迭代运算占用更多的系统资源与时间,且离散之后产生二值序列的随机性往往受限于离散算法的优劣.相比之下离散混沌在这方面就具有天然的优势.但是离散混沌也有其不足之处,如目前比较经典的logistic映射、cubic映射以及各种由它们衍生出来的一维映射[7-8],其共同点都是结构复杂性不高,系统参数少且混沌参数区间小,致使密钥空间窄.为增加混沌的复杂性,文献[9]提出了Henon映射,它是一个二维映射但是它仅包含一个平方非线性项.文献[10]提出将两个离散映射级联在一起,将一个混沌的映射区间嵌入到另一个混沌的初值区间中.本文则在logistic映射和cubic映射基础上,提出一个新的二维混沌映射,系统包含一个二次非线性项和一个乘积非线性项,同时有6个可变参数,扩展了密钥空间.并利用该离散混沌系统设计了一个简单的灰度加密算法,应用到图像灰度加密中,在实际应用中对比分析了logistic加密、henon加密以及新二维映射算法的安全性.
1新的二维超混沌离散混沌
本文提出的二维离散映射是将logistic映射和cubic映射进行改进融合在一起.其中,logistic映射为
x(n+1)=ux(n)(1-x(n))
(1)
cubic映射为
x(n+1)=ax(n)3-bx(n)
(2)
将式(1)与式(2)合并,改进后的二维映射如下:
(3)
式中,μ∈[0,4],a∈[0,4],b∈[0,3],c∈[0,4].
当μ=1.8,a=0.5,b=1,c=1,x(0)=0.1,y(0)=0.1时,二维映射产生混沌现象.图1为x(n),y(n)的迭代波形图.图2为x(n)与y(n)形成的吸引子相图.
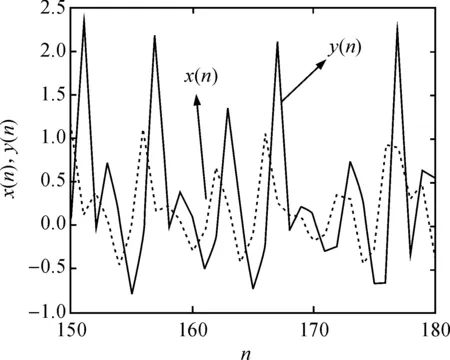
图1 x(n)与y(n)迭代波形图
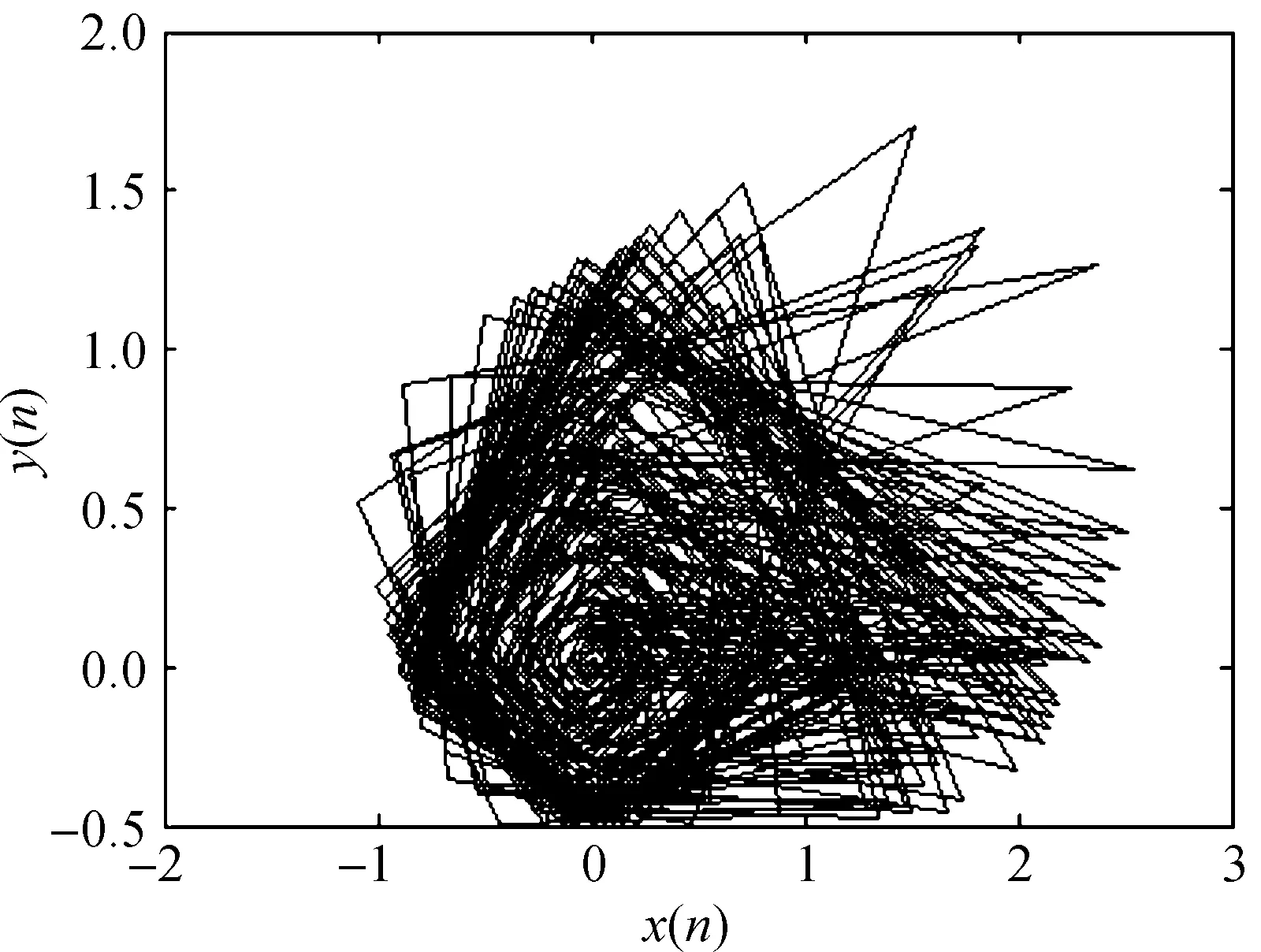
图2 映射吸引子图
2混沌特性分析
2.1Lyapunov指数与分叉图
Laypunov指数是系统是否产生混沌的一个重要判据,为进一步探索该系统动力学特性,本小节结合logistic映射和cubic映射对本映射系统进行Laypunov指数以及分岔图分析.
图3为3个离散映射的Laypunov指数图,Laypunov指数大于零表示系统处于混沌态.图4为3个混沌系统的分岔图.
取logistic映射中的可变参数u∈(0,4),令式(1)中x(0)=0.5,得到其Laypunov指数和分岔图分别为图3(a)和图4(a)所示;取cubic映射中的可变参数b∈(0,3),令式(2)中a=4,x(0)=0.1,得到其Laypunov指数和分岔图分别为图3(b)和图4(b)所示;取二维映射系统中的可变参数a∈(0,4),令其它参数不变,得到新二维映射的Laypunov指数和分岔图分别为图3(c)和图4(c)所示,在a∈[0.75,4]内存在2个正的Lyapunov指数LE1和LE2,产生超混沌现象.
具体混沌区间参数以及Laypunov指数参数如表1所示.对比图3中(a),(b),(c)可得到表1中Laypunov大于0的混沌区间,经过比较可以得出二维映射参数的混沌区间是大于logistic和cubic映射的.并且二维映射处于(0.75,4)时2个Laypunov指数全部大于0,出现了超混沌态,这对于二维离散混沌是一个非常重要的特性.从图4中可以得到,3个映射系统混沌区间中,新二维映射的区间明显大于前两者,同时在最大映射区间分布方面二维映射也大于2个一维映射.综合上述两方面分析,表明二维映射的混沌特性优于logistic映射和cubic映射.
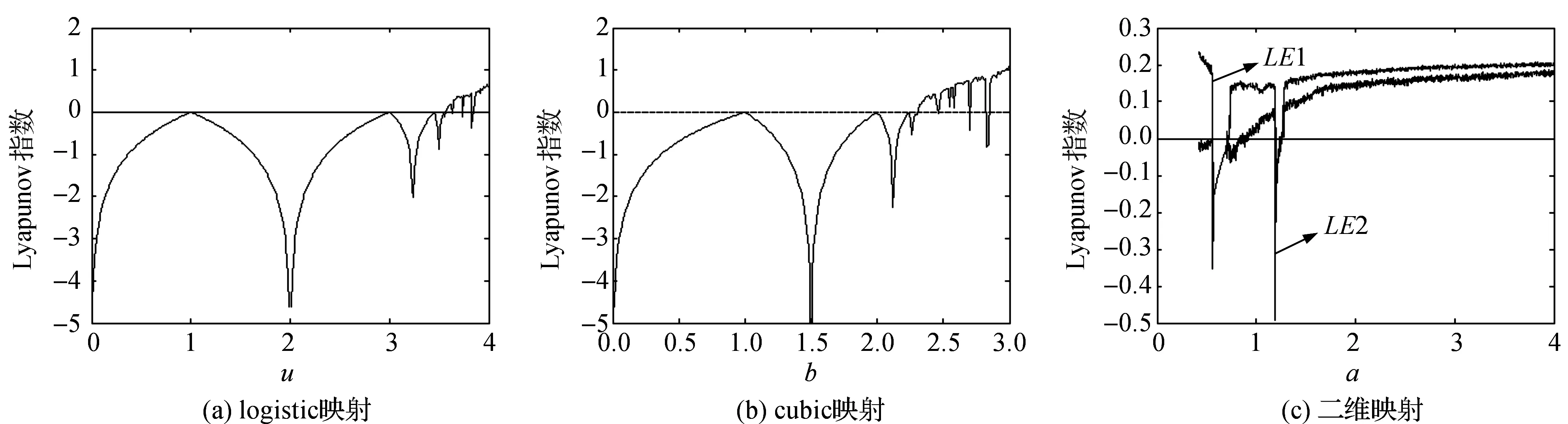
图3 Laypunov指数图
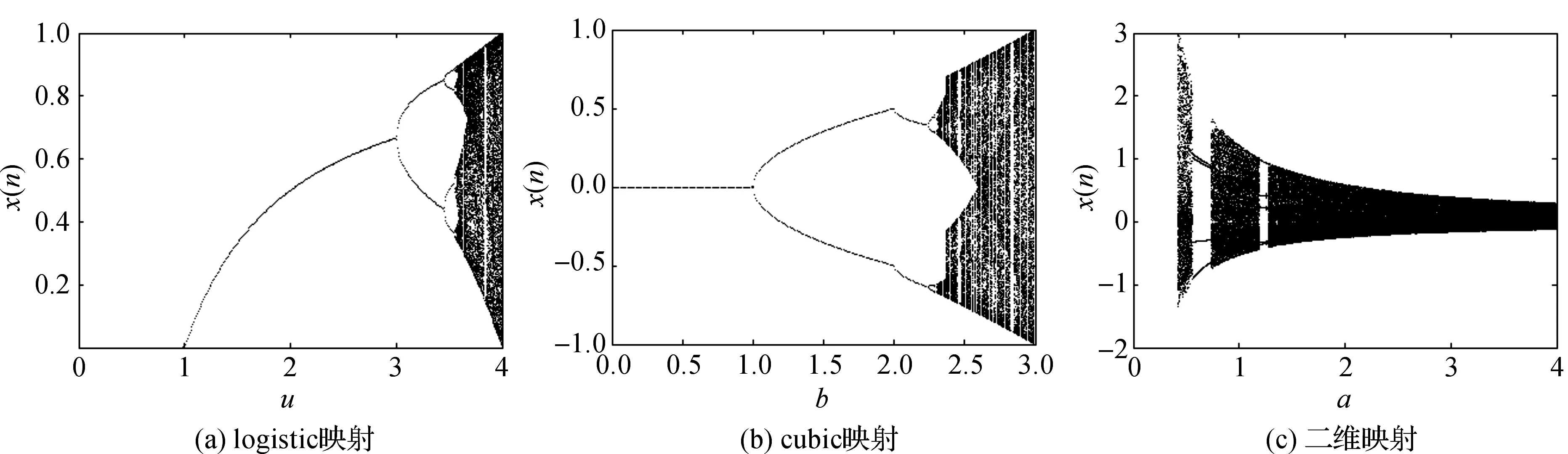
图4 分岔图

特性项混沌区间logistic映射cubic映射新二维映射Laypunov大于0的混沌区间(3.57,4)(2.31,3)(0.4,0.55)∪(0.75,4)最大映射区间(0,1)(-1,1)(-1,3)
2.2映射特性分析
图5为3个离散映射的映射图,其反映的是x(n)与x(n+1)逐次迭代产生的离散集合.图5中,(a)为logistic的映射图,类似于1条二次曲线;(b)为cubic的映射图,类似于1条三次曲线;(c)为二维系统的映射图,其图形不再类似于1条线,而是类似于1个平面.
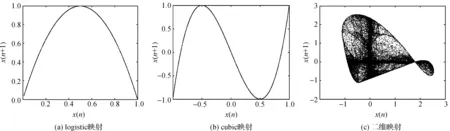
图5 x(n)之间的映射图
图5(a)与(b)均为一维离散映射图,由x(n)能够得到唯一的x(n+1),当处于混沌状态下x(n)之间是不存在x(i)=x(j)(i≠j)的,所以理想情况下,两者的图形都为1条无限接近于二次或者三次曲线的离散集合.但是实际情况下受限于计算机精度的影响不会无限接近,当超出计算精度时就会出现x(i)=x(j)(i≠j)情况,产生周期现象.
图5(c)为二维映射图,由x(n)与y(n)得到唯一的x(n+1),每进行1次迭代,x(n)到x(n+1)的映射函数都随着y(n)进行改变,不再像图5(a)和(b)那样是固定的映射函数,这就是映射图不再类似于1条线而是类似于1个平面的原因.此时当受计算机精度位数的影响,将小数点16位之后的数字忽略就会产生x(i)=x(j)(i≠j),映射函数也会因为y(i)≠y(j)(i≠j)而不同,系统仍然不会进入周期态,当然也不排除此时y(i)也受到到精度的影响恰巧y(i)=y(j)(i≠j)而进入周期态.综合上述分析,二维映射虽然不能避免受计算机精度影响,但是相比于一维映射可以降低其影响.
2.3NIST伪随机特性测试
为检测新混沌系统伪随机特性的优劣,本小节对logistic映射、cubic映射以及文章提出的二维映射分别作了NIST测试.采用相同的方法对这3个混沌系统二值化.步骤如下:
1)取伪随机数的小数点后5位数字;
2)将每位数字大于等于5取二进制的1,小于5取二进制0,从而得到5位二进制数;
3)循环迭代2×108次,得到1×109的二进序列.
采用美国国家技术标准局NIST推出的测试标准对产生的二进制序列进行了随机性测试[11].NIST评判序列性能的依据是:1)序列的通过率需大于0.96;2)P_VALUE值的均匀性大于等于0.000 1时,表示被测试序列的分布是均匀的.NIST测试结果如表2所示.
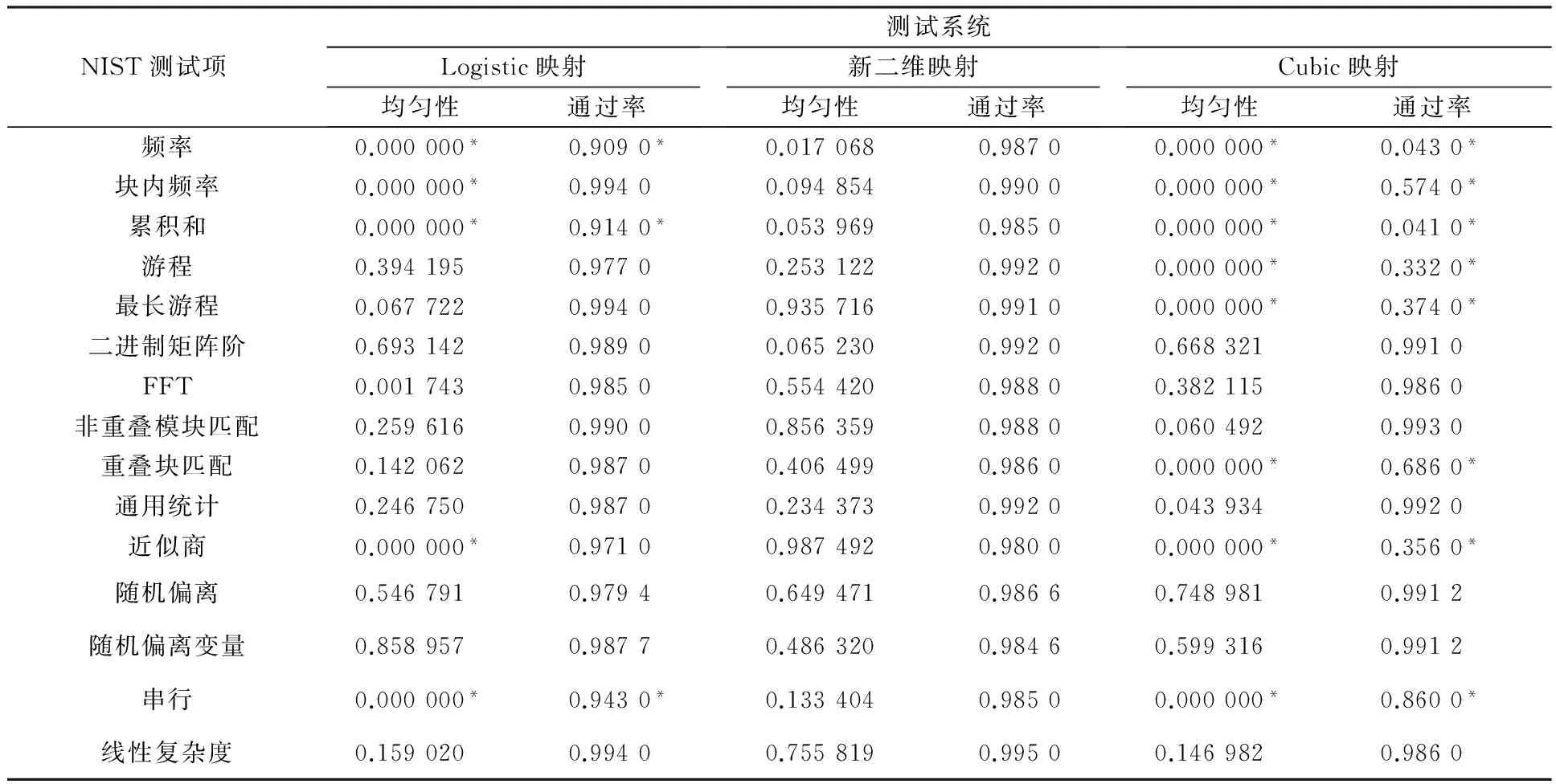
表2 伪随机序列NIST测试结果
表2中,带*的表示未通过检测的项,3个系统对比分析可得,logistic和cubic映射分别有5项和8项没有通过,本文提出的二维映射全部通过,表明本文提出的二维映射的伪随机性优于logistic映射以及cubic映射.
3二维离散混沌系统在图片加密中的应用
3.1混沌加密算法设计
定义图像像素点为m×n个,其中B(i,j)为第i行j列的像素值,加密算法如下:
4)K(i,j)=Kx(i)⊕Ky(j)i=1,…,m;j=1,…,n
5)M(i,j)=K(i,j)⊕B(i,j)i=1,…,m;j=1,…n
此算法的构造基础就是利用二维混沌序列x(i)和y(j)构造了1个m×n行的秘钥矩阵,使之与像素矩阵异或.参数a,b,c,μ为密钥参数.其优势是将混沌迭代的时间复杂度由o(m×n)降低到了o(MAX(m,n)).图6为利用上述算法的加解密结果.

图6 利用二维离散混沌系统的加解密图
3.2安全性分析
3.2.1密钥空间分析
在matlab平台下32位计算机的计算精度一般为10-16,因此加密算法中增加1个密钥其密钥空间就会增加1016倍.3个映射系统的密钥参数、密钥空间统计表如表3所示.由表3得出,新二维映射加密算法的密钥空间为1096,能很好地抗击唯密文攻击,同时得出新二维映射加密算法的密钥空间明显大于logistic映射和henon映射加密算法.

表3 logistic,henon映射和新二维映射密钥参数、密钥空间统计表
3.2.2相关性分析
为检验原始图像和加密图像相邻像素的相关性,分别从水平、垂直和对角方向,在图像中随机选取10 000对相邻像素,3个离散加密系统在3个方向加密前后像素的相关系数如表4所示.由表4可以得出3个加密系统都很好地掩盖了像素之间的相关性.

表4 相关系数统计表
3.2.3密钥敏感性分析
密钥敏感性在一定程度上反映了混沌加密算法抗穷举攻击的能力[12],为探索加密算法密钥敏感性,分别对3个系统中的初始值密钥参数x(1)做10-16的微小改变,其它密钥保持不变,对加密图像进行解密.图7中(a),(b),(c)分别为logistic,henon映射和新二维映射算法解密结果.由图7可以看出,在初值密钥x(1)敏感性方面新二维映射优于henon二维映射以及logistic映射.
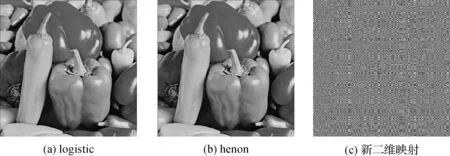
图7 初始值x(1)敏感性测试结果
分别取logistic映射的参数u,henon二维映射的参数a,新二维映射的参数a,使它们分别进行10-16的微小改变,其余密钥参数保持不变,对加密图像进行解密.图8中(a),(b),(c)分别为3个系统的解密结果.由图8表明在选取的3个参数密钥的敏感性方面,新二维映射和henon二维映射优于一维logistic映射.综合上述分析新二维映射具有较好的密钥敏感性.

图8参数敏感性测试结果
4结束语
本文从一维logistic映射和cubic映射出发,针对一维映射映射区间窄以及参数空间小的缺点,提出了一种新的二维离散映射.经过分析表明,本文提出的二维映射能够产生超混沌现象,这对二维离散映射具有重要的意义.同时,新二维映射相比logistic映射和cubic映射能够很好的降低计算机精度对混沌周期性的影响.最后将新二维映射应用于图像加密中,通过对比分析之前较为常见的logistic加密算法和henon加密算法,得到新二维映射在密钥空间和密钥敏感性方面优于logistic和henon映射,同时新二维映射加密算法降低了映射迭代的时间复杂度,缩短了加密时间,使算法更具有实用性.综合上述分析表明新二维映射具有较好的混沌特性以及广泛的应用前景,未来可以不断探索多维的离散混沌映射.
参考文献
[1]CHUA L. Memristor, Hodgkin-Huxley, and Edge of Chaos[J]. Nanotechnology, 2013, 24(38): 383001.
[2]JUNASNGSRI P,LOMBARDI F.Design of a Hybrid Memory Cell Using Memristance and Ambipolarity[J]. Nanotechnology,IEEE Transaction on,2013,12(1):71-80.
[3]王大朋,王光义,贺洁玲.双指数混沌系统及数字化实现研究[J].杭州电子科技大学学报,2013,33(5):1-4.
[4]LORENZ E N.Deterministic nonperiodic flow[J].Journal of the atmospheric sciences, 1963, 20(2):130-141.
[5]王光义,丘水生,许志益.一个新的三维二次混沌系统及其电路实现[J].物理学报,2006,5(7):3295-3301.
[6]邓斌,王忠林,侯承玺,等.一个四翼混沌系统的设计与实现[J].济南大学学报(自然科学版),2010,24(4):402-406.
[7]MAY R M.Simple mathematical models with very complicated dynamics[J].Natures, 1976,261(5560):459-467.
[8]DAMGÅRD I B,FRANDSEN G S.Efficient algorithms for the gcd and cubic residuosity in the ring of Eisenstein integers[J].Journal of Symbolic Computation,2005,39(6):643-652.
[10]王光义,袁方.级联混沌及其动力学特性研究[J].物理学报,2013,62(2):020506.
[11]ANDREW R,JUAN S,JAMES N. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Application[EB/OL].(2010-09-16)[2015-10-1].http://csrc.nist.gov/publications/PubsSPs.html#800-22.
[12]CHEN G, ZHAO X Y, LI J L. A Self-Adaptive Algorithm on Image Encryption[J].Journal of Software, 2005, 16(11):1975-1982.
DOI:10.13954/j.cnki.hdu.2016.03.002
收稿日期:2015-10-13
基金项目:国家自然科学基金资助项目(60971046,61281230357);浙江省自然科学基金重点资助项目(LZ12F01001)
作者简介:崔明章(1990-),男,山东济南人,硕士研究生,非线性电路域智能信息处理.通信作者:王光义教授,E-mail:wanggyi@163.com.
中图分类号:TN919.81
文献标识码:A
文章编号:1001-9146(2016)03-0006-06
A New Two-dimensional Discrete Hyperchaos Mapping and Its Application in Image Encryption
CUI Mingzhang, WANG Guangyi, REN Guorui, JIN Peipei
(SchoolofElectronicInformation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:Based on logistic mapping and cubic mapping, for one dimensional mapping chaotic narrow range and simple of mapping function, this paper proposes a new two-dimensional discrete hyperchaos mapping. The chaotic interval of system’s parameters is greater than the logistic mapping and cubic mapping, mapping domain is also greater than before, and there are two positive Laypunov indexs with having a hyperchaos phenomenon that. Iterative operation affected by the precision of computer is less than one dimensional mapping. The binary pseudorandom sequence of mapping is tested by NIST, resulting shows that the randomness of two-dimensional mapping is much better than logistic mapping and cubic mapping. Finally, putting forward a grayscale image encryption algorithm based on the two-dimensional mapping. The algorithm is compared with the logistic and Henon encryption increases the key space, reduces the time complexity of mapping iterative.
Key words:two-dimensional discrete; pseudo random; hyperchaos; image encryption
