两相异步电机的数学模型及动态特性仿真

汪　敏

(江汉大学 数学与计算机科学学院， 武汉　430056)



两相异步电机的数学模型及动态特性仿真

汪敏

(江汉大学 数学与计算机科学学院， 武汉430056)

摘要：通过对两相异步电机绕组结构的分析，在理想化假设的情况下推导了两相电机的电磁关系，建立了电机在任意速旋转坐标系dqn下的通用数学模型，并在分析电机数学模型的基础上，应用搭建模块法建立了Matlab/Simulink软件环境下两相异步电机的动态模型．并以实际应用中的小功率电机为例，对电机运行进行了仿真分析．对其启动后突加负载及带负载启动等多种瞬态过程进行了仿真计算．仿真结果表明应用此数学模型对电机运行过程进行仿真具有较高的精度、较好的通用性等优点，具有一定的实用价值．

关键词：两相异步电机；dq变换；Simulink仿真

0引言

小功率单相异步电机在家用电器和工农业生产中获得了广泛应用[1-3]，如水泵、空调、洗衣机等设备所采用的单相异步电机结构具有结构简单、控制方便、运行可靠等优点．小功率异步电机很多场合都希望能调节速度，比如空调用电机运行于高精度温度调节、洗衣机运行于洗衣或者甩干模式时，都希望电机能在很宽的范围内调节速度，同时又希望电机的输出转矩不要出现太大的波动，很显然单相电机偏软的机械特性已不能满足实际需求，由于单相电机只有一个主绕组，通电后所产生的磁场是脉振磁场，不是旋转磁场，不能使鼠笼式转子产生启动转矩．因此一般利用电容启动的单相异步电机都设置了一个在空间上与主绕组相差90°电角度的副绕组，利用交流电路中电容的电流超前电压90°相角这一原理产生旋转磁场．单相异步电机的这种结构导致调速控制方法受到很大的限制，实际控制中一般采用较为简单的调压或调频的方式，其转速调节密度较低，导致效率低、经济性差；在实行变频调速时，频率变化将导致电机内部磁场由圆形变成椭圆，造成转子转矩波动，电机运行效率降低，不能满足家电和工业用电机不断增长的性能需求[4-6]．

而采用对称绕组的两相异步电机则可以解决以上这些问题，两相异步电机内部有两个主绕组，可用变频器输出对称两相电压来直接驱动，因此可以实现精确、灵活而连续的速度控制，并且运行非常平稳．随着电力电子技术、微处理器及现代控制技术的发展，实现两相异步电机的变频调速系统非常方便，同时具有结构简单、运行可靠、调速性能好、工作寿命长等优点．既可以获得和三相异步电机相近的动态性能，结构又相对简单．

1两相异步电机参数的确定

两相异步电机绕组由定子绕组和转子绕组两部分构成，定子绕组采用相差90°电角度的结构，转子绕组采用鼠笼式结构．两相异步电机是一个高阶、强耦合、非线性的多变量系统，其基本结构如图1所示，由理想化电机的假设可以推导出两相异步电机的绕组电感．

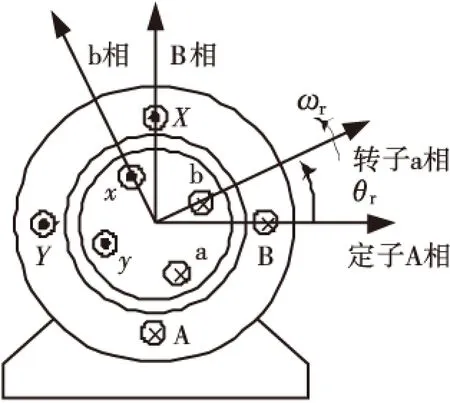
图1　两相异步电机结构

异步电机的基本模型参数计算中，对于p对极电机x相绕组和y相绕组电感系数lxy的一般化计算公式为[2]：

(1)

式中，Λg为气隙磁导，Nx，Ny分别为x绕组和y绕组的匝数，αxy为x绕组和y绕组轴线的夹角．

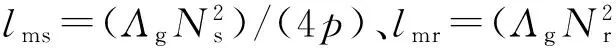
(2)

定、转子绕组之间的互感矩阵为：

(3)

式中，θr为定、转子绕组之间夹角．可以看出两相异步电机与三相异步电机的数学模型的区别在于两相电机定子绕组两相之间和转子绕组两相之间互感为零，消除了耦合．

2dqn坐标系中的数学模型

建立旋转坐标系如图2所示[2]，从相坐标系到dq坐标系的变换矩阵为：

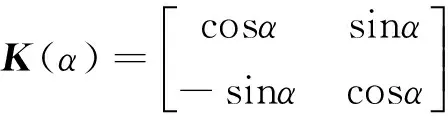
(4)

式中，α为d轴与定(转)子A(a)相绕组轴线之间的夹角．

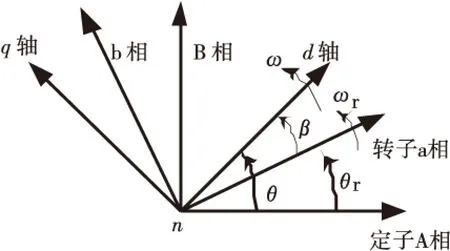
图2　相坐标系和dq坐标系

由旋转变换得dq坐标系中的磁链方程为：

(5)

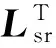
(6)

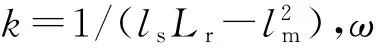
3静止坐标系下模型的构建

忽略电机内部的铁磁损耗及磁饱和等因素可以简化电机模型，在静止坐标系中以定子电流和磁链作为状态变量建立两相鼠笼式异步电机的动态数学模型，由式(6)中的数学模型[7-8]得两相异步电机在αβ静止坐标系下的表达式：

(7)

(8)

电磁转矩和转子运动方程为：

(9)

(10)

式中，Te、TL为电磁转矩、负载转矩；np为电机极对数；J为转子转动惯量．

可以在Simulink中利用丰富的模型库建立两相鼠笼式异步电机的数学模型，将电机模型分解为独立的子模块，由式(7)(8)建立定子侧α轴电流、磁链仿真子系统如图3所示，类似地可以建立定子侧β轴电流、磁链仿真模块、转子侧α轴电流、磁链仿真模块和转子侧β轴的电流、磁链仿真模块如图4～6所示．

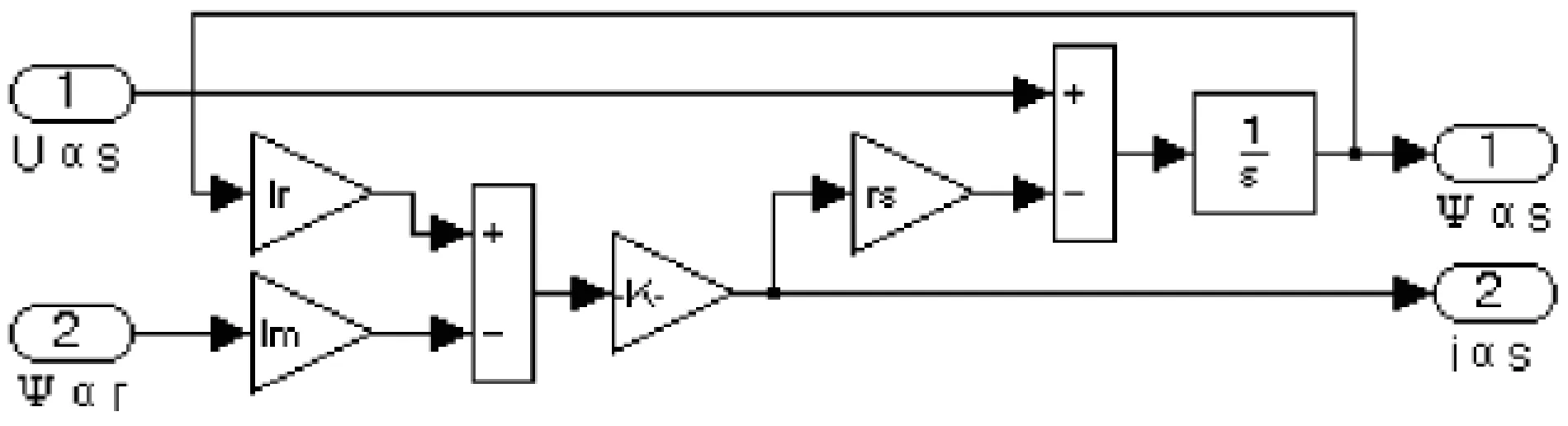
图3　定子侧α轴的电流、磁链仿真子系统

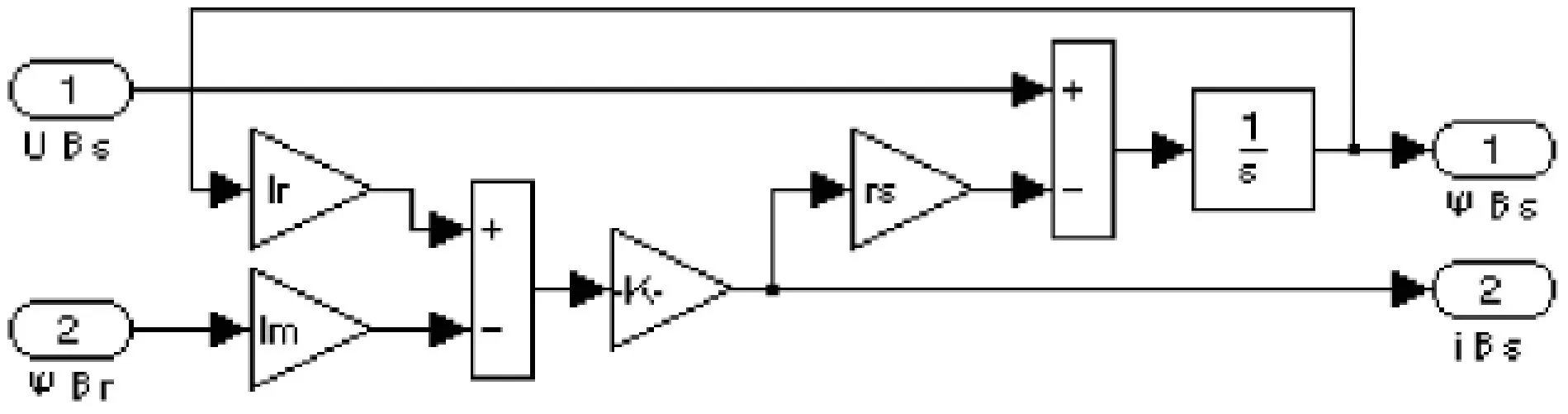
图4　定子侧β轴的电流、磁链仿真子系统

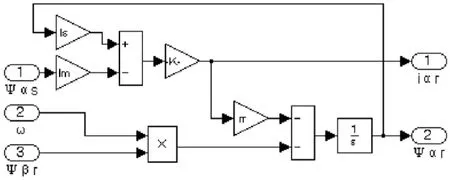
图5　转子侧α轴的电流、磁链仿真子系统

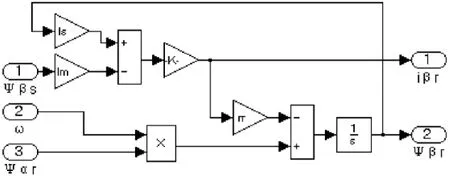
图6　转子侧β轴的电流、磁链仿真子系统

根据两相异步电机数学模型中的电磁转矩方程式(9)(10)，可建立电机电磁转矩及转子运动仿真子系统如图7所示，图中Te为电机输出转矩，TL为负载转矩．

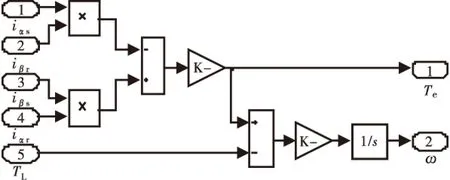
图7　电磁转矩仿真子系统

由两相异步电机的数学模型和Simulink信号流图，可以建立两相异步电机的仿真模型如图8所示．

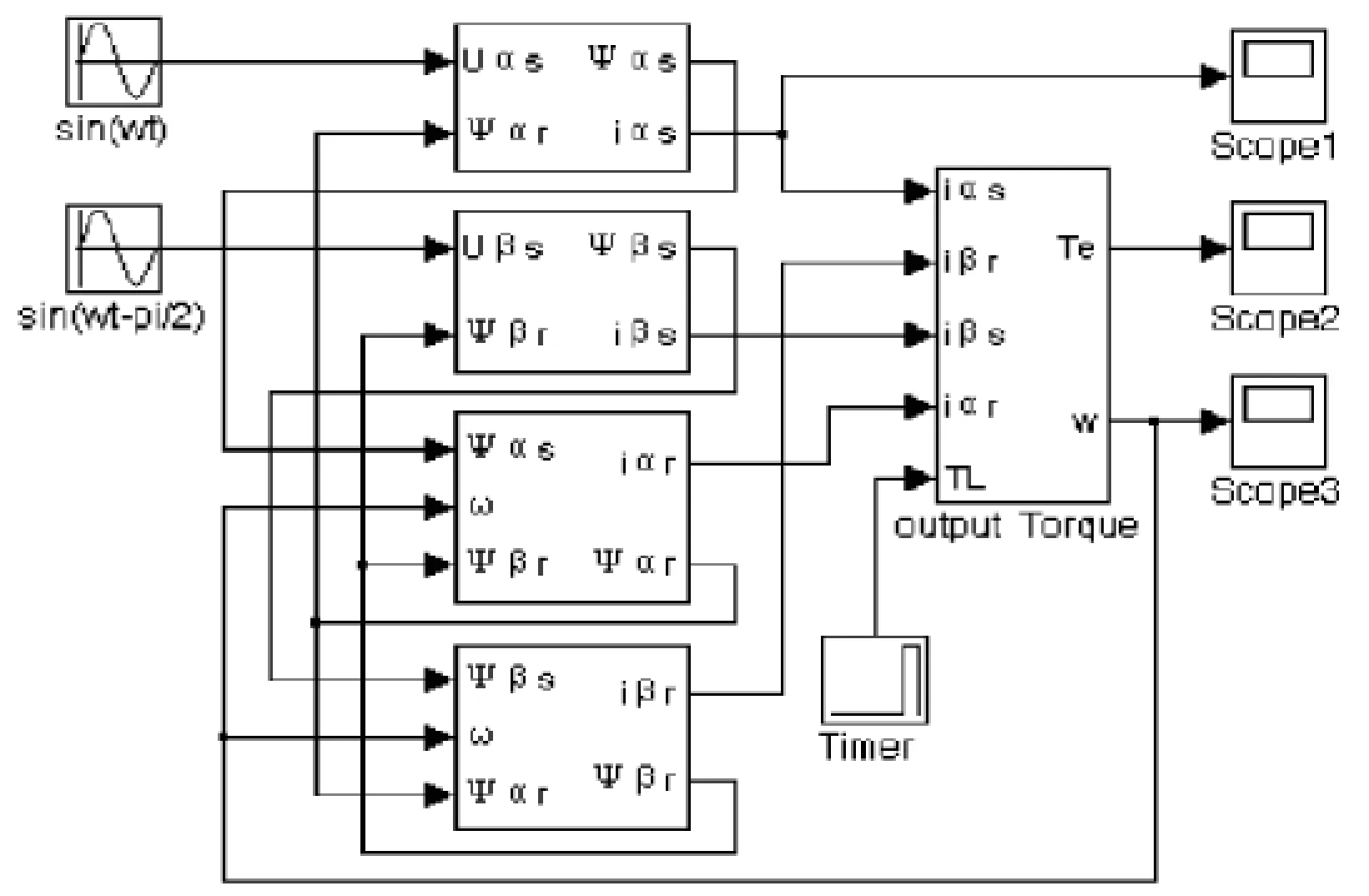
图8　两相异步电机的仿真模型

4实例仿真

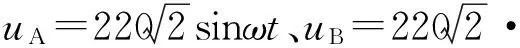
1) 空载启动，在0.5～0.6 s时间段加上6 N·m负载，定子A相电流、电磁转矩Te、转子转速ω如图9所示．

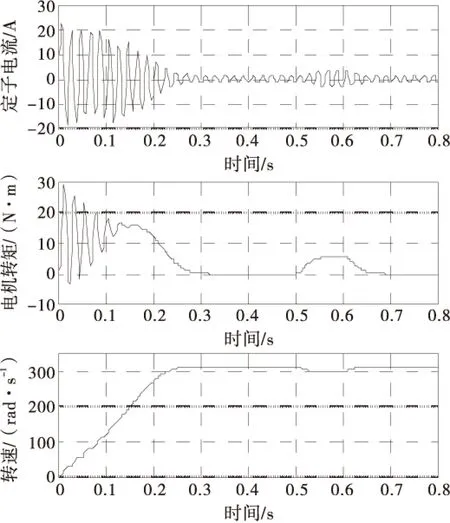
图9　空载启动后加负载的仿真波形

空载启动时，起动过程冲击电流较大，幅值可达额定值的4倍，电机转速在0.3 s左右上升到额定值，0.5～0.6 s加上负载时电机转速开始下降，电磁转矩迅速上升，具备很强的转矩跟踪能力，负载波动造成的影响能很快消除，转速下降幅度很小，并能很快恢复到稳定值．这主要是由于电机具备较大的惯性，稳定运行时态已存储一定的电磁能和机械能，因此负载突变造成的影响不明显．

2)电机带负载启动，负载转矩为6 N·m，a相电流、电磁转矩Te、转子转速ω仿真结果如图10所示．

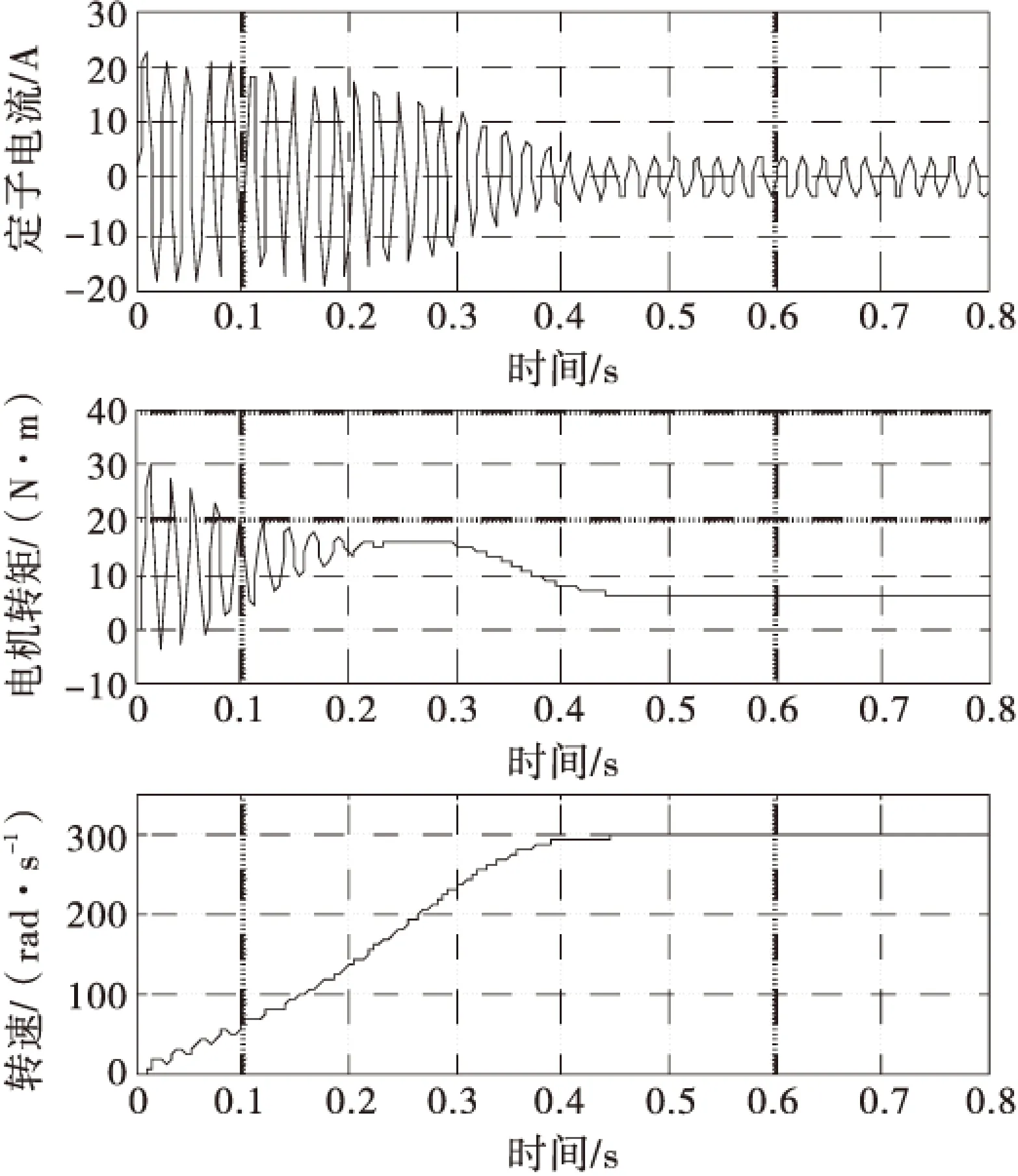
图10　带负载启动时的仿真波形

带负载启动时电机冲击电流比较大，和空载启动时相比电流持续时间和转速上升到稳定值的时间都相对有所延长，大概需要0.4 s左右，有转矩扰动时，两相异步电机只需0.2 s左右就能达到新的稳态．在启动转矩波动及稳定性方面有很大提升．仿真结果验证了模型的有效性，由于两相异步电机的定子磁链轨迹接近圆形，启动转矩大，转速上升快，消除了单相异步电机中脉动磁场缺陷而导致的较大幅度的转矩脉动，运行更加平稳，理论上稳态运行可以保证机械转矩恒定；同时两相结构和单相相比，具有较大的空间利用率，可以获得更大的功率密度，因此可以获得较强的带载能力，带负载启动时，电流和转矩脉动较小；稳态运行时，抗干扰能力也很强．

目前单相异步电机的控制主要通过控制电磁转矩和磁链来实现，将转矩和磁链经坐标变换后等效为直流电机进行控制．由于主副绕组匝数的不对称性，磁链矢量不能以固定幅值旋转，使电机内部磁场为椭圆型磁场而非圆形磁场，因此单相异步电机运行中转矩脉动较大．而采用两相模型的异步电机系统，很好地消除了磁场脉振、转矩脉动过大等问题，由数学模型可知两相结构内部磁场为圆形磁场，稳态运行没有转矩脉动，采用两相结构的电机模型具有良好的运行稳态性能，控制精度高，实用性较好．

5结语

介绍了两相异步电机矢量变换的数学模型，并在Simulink环境下建立了电机的数学模型并完成了仿真分析，采用该两相异步电机的仿真模型，可以十分便捷地对两相电机的启动性能进行了分析和仿真，得出该交流电机的转矩、转速等运行曲线，波形符合理论分析．

仿真结果表明两相异步电机具有较好的静态、动态性能，同时两相异步电机驱动系统可由变频器直接产生对称两相电压，直接驱动两相绕组，采用对称绕组的两相异步电机和三相异步电机相比，结构相对简单，却能够获得和三相异步电机相近的动态性能．两相异步电机可以克服单相电机转矩脉动的情况，在功率较大的情况下有明显的优势，可应用在空调、水泵等设备上，能在满足性能要求的前提下降低系统成本．

参考文献：

[1]傅海涛,杨长安．两相异步电机的动态特性仿真[J]．中小型电机，2005，32(4)：10-13．

[2]辜承林.机电动力系统分析[M]．武汉：华中科技大学出版社，1998．

[3]顾德英，季正东，张平．基于Simulink的异步电机的建模与仿真[J]．电力系统及其自动化学报，2003，15(2)：71-73．

[4]Yu X，Dunnigan M W，Williams B W．A novel rotor resistance identification method for an indirect rotor flux orientated controlled induction machine system[J]． IEEE. Transactions on Power Electronics，2002，17(3)：353-364．

[5]Avdiu N Z． Modeling of the induction motor with two sets of three phase windings in the stator and squirrel cage rotor. IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society[J]． IEEE Conference Publications, 2012 , 1900-1907．

[6]杨祖泉，姚绪梁，舒小芳．异步电动机直接转矩控制系统的仿真研究[J]．电机与控制学报，2004,8(4)：329-332．

[7]周力求，等．基于MATLAB/SIMULINK的异步电动机建模与仿真[J]．电机电器技术，2003(4)：32-35．

[8]Jezernik K． Robust Induction Motor Control for Electric Vehicles. Advanced Motion Control[C]． Tsu-City, Japan：1996. AMC '96-MIE. Proceedings．

[责任编辑张莉]

收稿日期：2015-09-06

通信作者：汪敏(1979-)，女，讲师，博士，研究方向为计算数学．E-mail： wangmin_6@163.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.017

中图分类号：TM343

文献标识码：A

文章编号：1672-948X(2016)02-0075-04

Dynamic Simulation and Mathematical Model of Two-Phase Asynchronous Motors

Wang Min

(School of Mathematics & Computer Science, Jianghan Univ., Wuhan 430056, China)

AbstractBased on analyzing the winding structure of two-phase asynchronous motor, the electrical and magnetical relationship has been deduced under an ideal assumption. The universal mathematical model under dqn coordinate turning at arbitrary angular velocity has been established. The simulation case of the two-phase asynchronous motor has been constructed under Matlab/Simulink environment. The starting and loading conditions have been simulated. The results demostrate that the two-phase asynchronous motor has characters of high accuracy and stability.

Keywordstwo-phase asynchronous motor；dq trasformation；Simulink