地铁盾构施工地层变形预测及数值分析

邱明明，杨果林，姜安龙，申　权

1)中南大学土木工程学院，湖南长沙 410075；2)厦门轨道交通集团有限公司，福建厦门 361001



地铁盾构施工地层变形预测及数值分析

邱明明1，杨果林1，姜安龙2，申权1

1)中南大学土木工程学院，湖南长沙 410075；2)厦门轨道交通集团有限公司，福建厦门 361001

摘要：以某城市地铁在建盾构隧道为研究对象，借助数值仿真建立了三维盾构施工有限差分计算模型，给出了盾构施工引起的地层变形三维地层损失预测方法，并对盾构施工地层竖向变形及水平变形计算结果进行对比分析. 结果表明，隧道横向地层变形接近“V”形分布，形成的地表沉降槽宽度约为6倍隧道直径；盾构前方土体产生隆起，开挖面后方表现为沉降，沿盾构掘进方向近似呈倒“S”形，并在开挖面前后3倍直径以外逐渐趋于稳定；地层水平变形左右两侧反对称，距隧道中心约1倍直径处地层水平变形值最大，6倍直径以外地层水平变形基本不受施工影响；随着埋深的增加，地层水平变形值减小，隧道拱腰上下一定范围土体向洞外移动.所得结论对城市地铁盾构隧道设计与施工变形控制有指导意义.

关键词：隧道工程；地铁； 盾构施工； 土体损失； 预测模型； 地层变形； 三维数值试验； 动态模拟

随着城市轨道交通建设的快速发展，盾构法逐渐成为一种被广泛应用于各种地质条件下修建隧道的施工方法，但其施工是在土体内部进行的，仍不可避免对周围土体产生扰动影响，引起隧道周围地层发生松动和变形，进而危及邻近建筑物安全或诱发诸多环境问题[1-2]. 因此，探讨盾构施工引起的地层移动和变形机理及规律，对盾构施工控制、变形预测及保护周围环境具有重要意义.

诸多学者曾致力于盾构施工变形的研究[3-14]，分别采用经验公式法[3-5]、理论解析法[6-13]、随机介质理论法[14-16]和数值分析法[17-20]等方法对这一问题尝试解答，取得了很多有益的成果. 其中，经验公式法简单明了、计算方便，被广泛应用于预测盾构隧道开挖引起的地表沉降，但这是建立在一种经验的基础之上，缺乏理论依据，应用具有一定的局限性. 实际上盾构法施工过程是一个复杂的动态三维问题，其施工过程中受开挖面支护力、盾尾间隙、壁后注浆和支护时间等因素的影响，使得对盾构施工变形这一问题的深入研究变得十分困难. 因此，借助数值仿真手段，对盾构隧道施工过程进行精细化数值模拟分析，对进一步掌握盾构施工过程力学行为及地层变形规律具有积极意义.

三维有限差分软件FLAC在处理动态、大变形和非线性等问题中具有较强的优势[21-23]. 本研究以某地铁区间隧道盾构施工为研究背景，考虑盾构施工过程中开挖、推进、支护力、注浆和支护等工序，采用FLAC软件建立三维盾构施工力学模型，探讨盾构施工引起的地层变形横向分布规律、地层变形纵向分布规律及深层土体水平变形规律. 同时，基于地层损失理论的基础之上，对盾构施工引起的地层变形进行三维预测，并结合数值计算结果进行对比分析. 研究成果可为地铁隧道设计和盾构施工控制提供参考.

1工程背景

某城市地铁区间盾构隧道，隧道起止里程为CK03+294.400～CK03+993.447，右线区间长699.047 m. 拟建场区沿线主要地层为近代人工填筑土层、第四系全新统海积层、海陆交互相沉积层、冲洪积层及残积层. 根据工程地质勘察报告，该段地层自上而下分布情况为：杂填土、素填土、中粗砾砂、残积砾质黏性土、全风化花岗岩、强风化花岗岩、中风化花岗岩和微风化花岗岩. 岩层埋藏于第四系地层之下，风化层厚度较大，且岩性、分布、厚度及性能变化较为复杂. 各土层的物理力学性质指标见表1. 其中，H为土层厚度； ρ为密度； φ为土体内摩擦角； c为黏聚力； E为弹性模量； ν为土体泊松比.

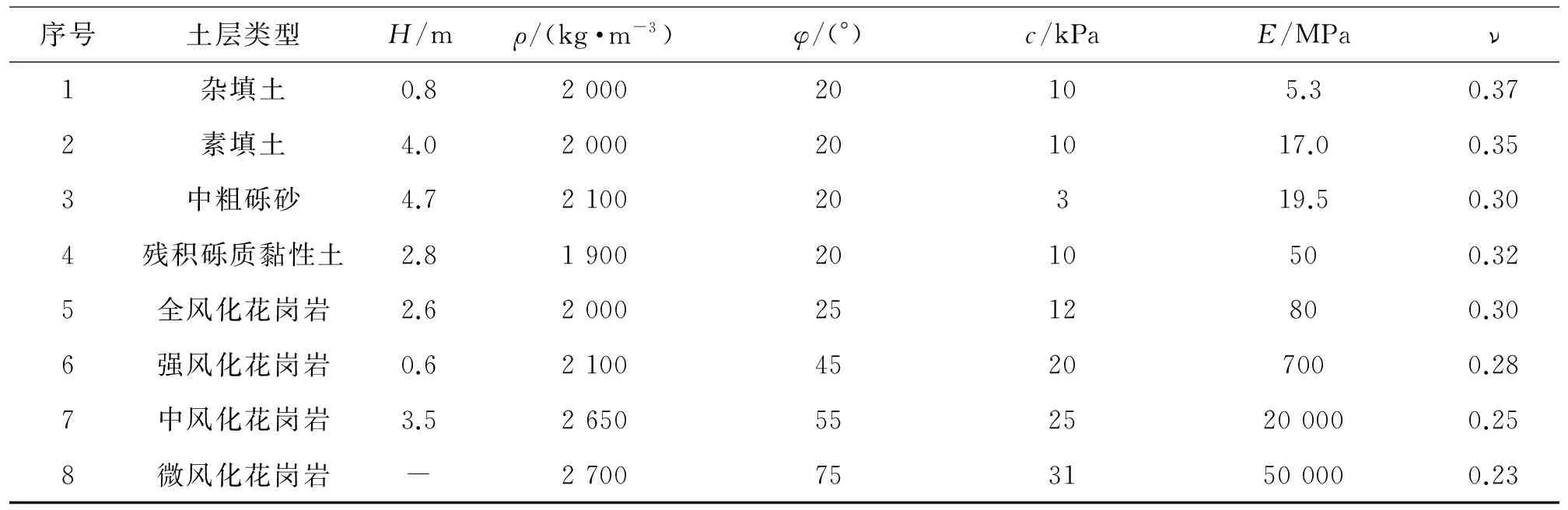
表1　土层物理力学参数

本次设计范围内区间右线穿越地层，主要为残积砾质黏性土、散体状强风化花岗岩和全风化花岗岩；隧道顶部地层为残积砾质黏性土和残积砂质黏性土. 区间隧道沿线均是城市主要干道道路，周边建筑物及地下管线较多，区间埋深变化较小，不宜采用明挖施工. 盾构法在该地层施工时，较矿山法经济、安全、合理，故采用盾构法施工.

区间隧道断面为圆形隧道，隧道衬砌管环外径为6.20 m，内径为5.50 m，环宽1.20 m，厚度为0.35 m. 采用单层衬砌，衬砌管环由一块封顶块、两块邻接块和三块标准块构成，采用预制装配式钢筋混凝土管片错缝拼装而成，管片之间连接采用弯螺栓连接.

2基于地层损失的地层变形预测

2.1地层变形计算方法

在众多地铁隧道盾构施工地表变形预测方法中以经验公式法应用最为广泛，而经验公式法又以Peck[3]提出的简捷方便的估算公式最为著名，其计算原理如图1. 该方法以统计有限区域工程实测数据为基础，系统地提出了地层损失的概念和隧道开挖引起的横向地表变形实用预测公式，即著名的Peck曲线，其表达式如式(1).

图1　地表沉降槽断面形状Fig.1　Sectional shape of surface settlement trough

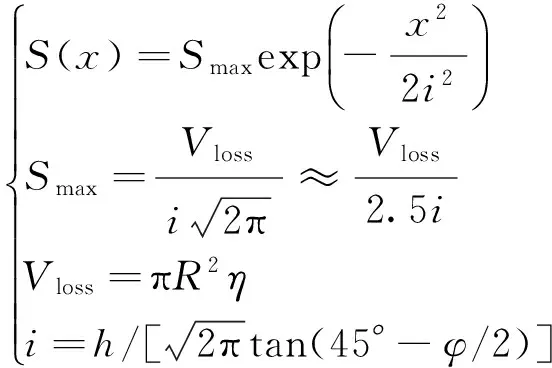
(1)

其中，S(x)为地表变形；x为沿隧道横向水平距离； Smax为地表最大变形；i为地表沉降槽宽度系数； R为隧道计算半径； Vloss为施工引起的隧道单位长度的地层损失量； h为隧道中心埋深； η为地层体积损失率，即单位长度地层损失占盾构开挖体积的百分比，其取值参考文献[24].

Sagaseta[6]在不排水条件下，假定土体是不可压缩的均匀弹性半无限体，土体损失沿轴线均匀分布，并将土体损失等效为圆柱体，推导了三维的地表变形解析解，其表达式为

(2)

Loganathan等[8]在文献[6]的基础之上，采用椭圆形非等量径向土体移动平面，提出了预测地层位移的二维解析解，其表达式为

其中， y为沿盾构推进方向的距离；z为距地表的深度；g为间隙参数；其他参数含义同式(1).

文献[12]基于地层损失理论的基础上，提出考虑土体泊松比以及椭圆形非等量径向土体位移模式的地表沉降计算公式：

(4)

根据文献[6, 8]的研究成果可知，盾构施工沿掘进方向的地层损失分布及地层损失率可表示为

(5)

参考式(3)和式(4)，并结合式(5)，可得地铁隧道盾构施工地层损失引起的三维地层变形预测模型为

(6)

盾构施工引起的地表沉降是反映周边土体移动变化直接的表现，也是工程中最为关注的问题之一. 当z=0时，式(6)即为盾构施工引起的的地表沉降预测公式，且与式(4)相同.

2.2实例验算

某城市地铁区间隧道盾构试验段，盾构施工主要穿越粗砂、砾砂、圆砾和泥质粉砂岩地层，采用辐条加泥式复合土压平衡盾构机，衬砌管片外径和内径分别为6.00 和5.40 m，管片宽度为1.20 m. 计算参数取值如下：R=3.20 m， h=15.80 m， φ=30.0°， c=5.0 kPa， ν=0.30， Es=6.40 MPa， η=1.00%.

采用不同方法计算得到的盾构地层损失引起的地表沉降曲线变化趋势较相近，见图2. 盾构施工引起的横向地表沉降呈“V”形沉降槽，沉降槽左右两侧基本对称，最大地表沉降发生在隧道中心正上方；盾构施工引起的纵向地表沉降曲线呈“S”形，开挖面前方隆起效应不明显，开挖面后沉降量先增大后趋于稳定；各方法所得的地表沉降最大值依次为-13.2、 -6.0、 17.7、 -17.0、 -20.6和-19.4 mm.可见，Sagaseta法计算的地表沉降值明显偏小，本研究方法所得结果与Loganathan方法、数值方法和现场实测结果较为相近，且可用于分析和评价盾构施工引起的三维地层变形.

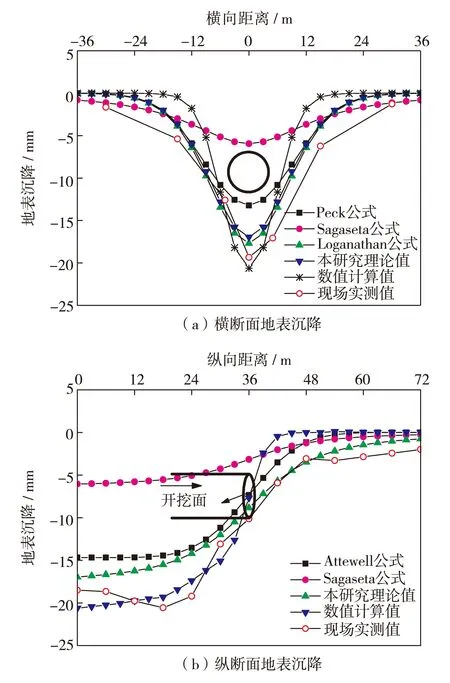
图2　盾构施工引起地表沉降曲线对比Fig.2　(Color online) Comparison of surface settlement curves by shield tuneling

3地铁盾构施工数值试验

3.1三维地层-结构计算模型

根据工程勘察报告及盾构隧道设计资料，其隧道直径D=6.4 m，模型上边界为地表，埋深h=13.3 m，取为自由边界；考虑隧道开挖影响区域3～5倍D最适宜，横向范围取36.0 m；模型下部取隧道底部下21.7 m；沿隧道推进方向长度取72 m(每环1.2 m，共计60环管片). 按照表1的土层分布情况，考虑模型的对称性和单元数量，建立的三维有限差分计算模型尺寸为(长)72 m×(宽)36 m×(高)35 m，模型共划分27 456个单元，30 184个节点.

模型四周限制水平移动，设为位移边界；模型底部限制水平和垂直移动，设为固定边界. 沿盾构隧道横断面方向为x轴，沿盾构推进方向为y轴，地层深度方向为z轴，建立三维坐标系，所建模型网格划分和隧道内部结构见图3. 其中，b为厚度.

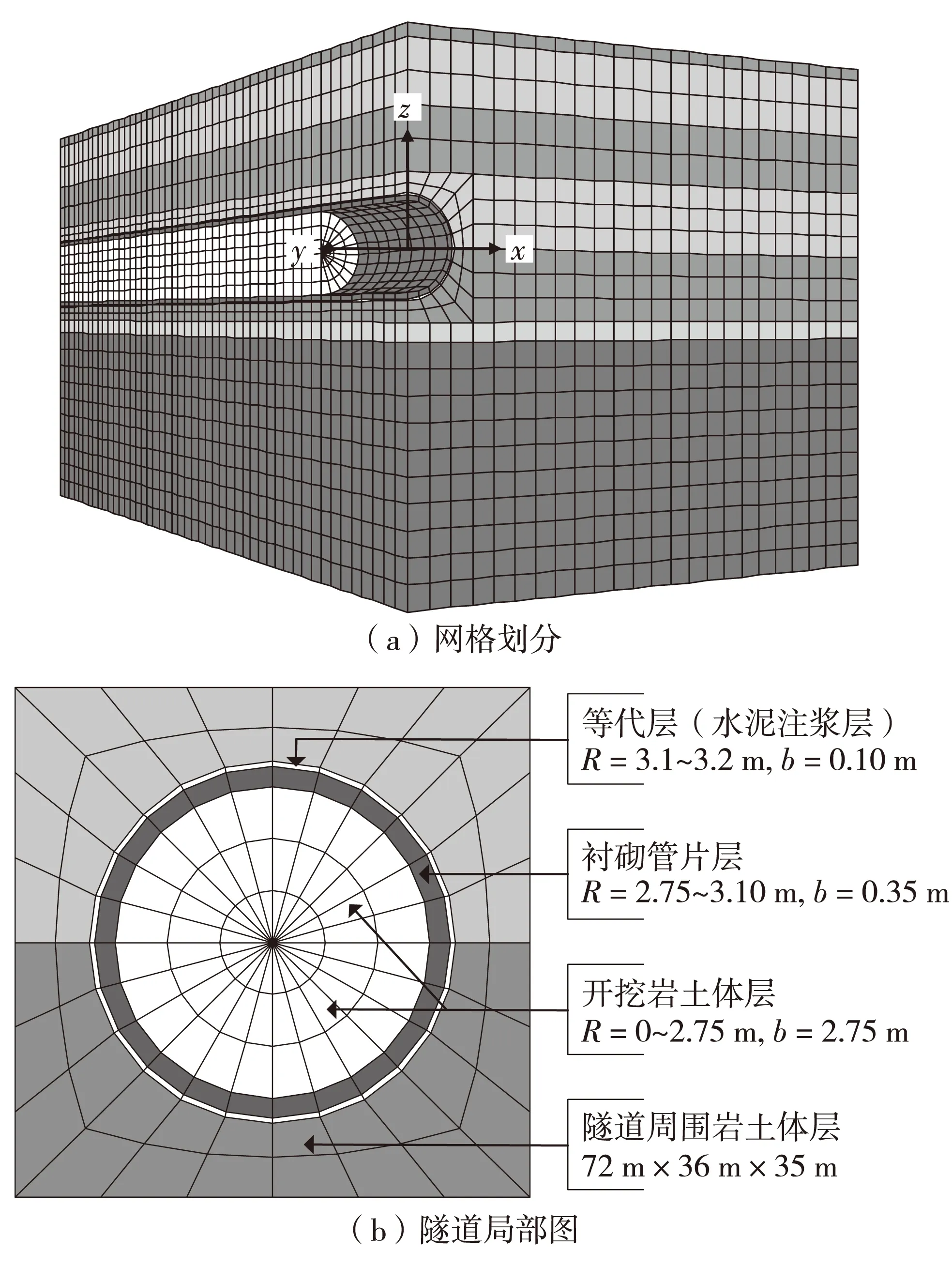
图3　三维数值计算模型Fig.3　Computational three-dimensional model

3.2材料模型

在数值计算过程中，土体采用实体单元模拟，其计算参数按表1取值. 考虑岩土体的非线性，材料强度准则采用Mohr-Coulomb弹塑性屈服准则，其表达式为

f=τn-c-σntanφ=0

(7)

其中， τn和σn分别为受力面上的剪应力和正应力.

M-C屈服条件在π平面上表现为一个不等角的等边六边形，其屈服面在主应力空间是一个棱锥面，且中心轴线与等倾线重合[25]，如图4. 其在三维应力空间中的表达式为

(8)

其中， I1为应力张量第1不变量； J2和J3分别为应力偏张量第2和第3不变量； τ8为八面体剪应力.

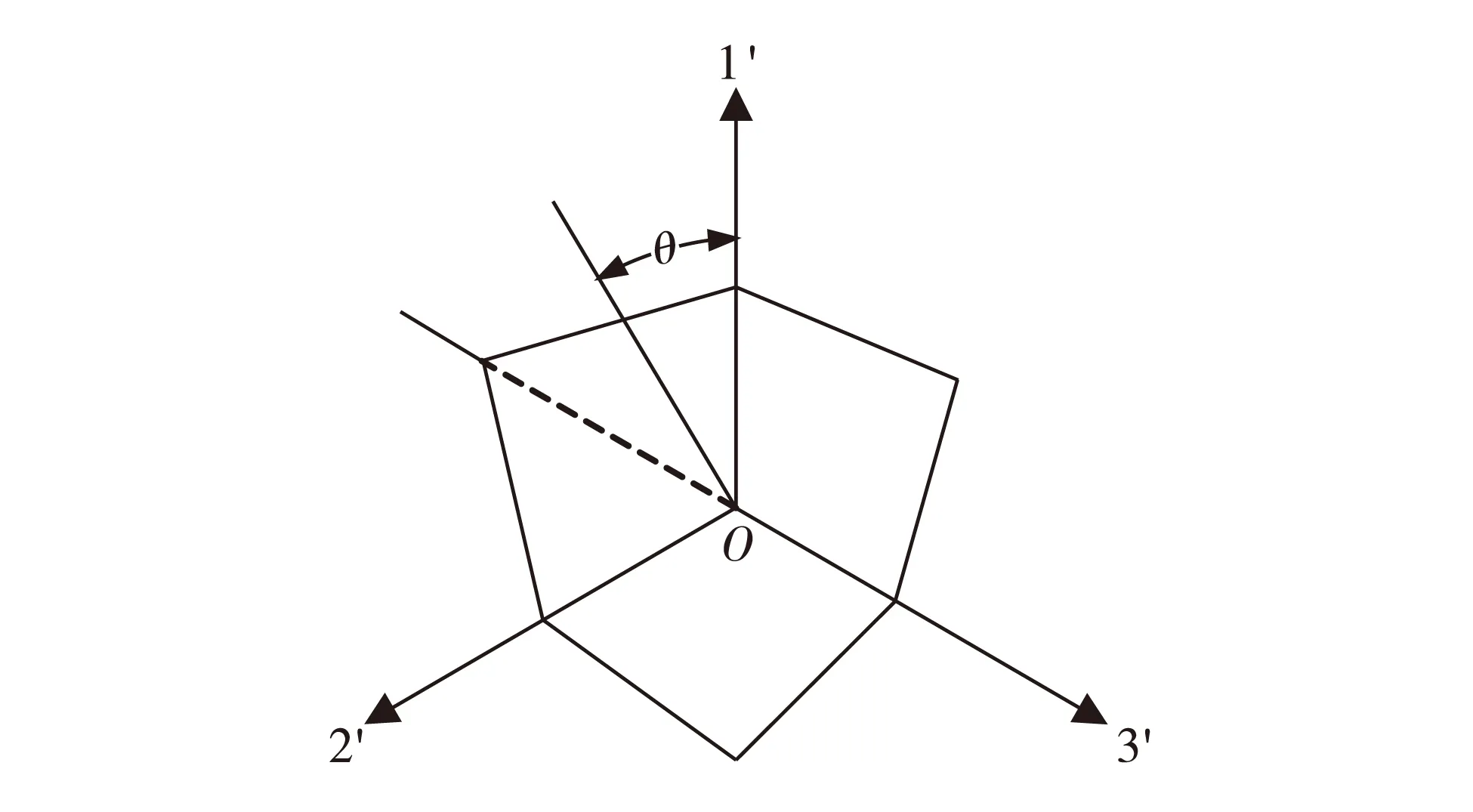
图4　Mohr-Coulomb屈服面Fig.4　Mohr-Coulomb yield surface

衬砌管片与围岩之间形成的盾尾间隙采用壁后注浆充填，壁后注浆圈层一般采用等代层来模拟[17]，本研究中等代层厚度取0.10 m. 衬砌管片采用C50钢筋混凝土，厚度为0.35 m，弹性模量为34.5 GPa，考虑管环接头效应，其刚度乘以系数0.85. 假定等代层和衬砌管片均为弹性材料，符合弹性本构关系，且均采用FLAC中的实体单元来模拟. 其材料属性通过体积模量K和剪切模量G两个弹性常量来描述，材料参数计算按式(9)进行换算[21]，支护材料力学参数见表2.其中， γ为容重.

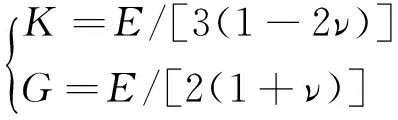
(9)

3.3盾构掘进过程的实现

通过对建立的三维数值计算模型施加重力荷载，清除自重作用下产生的土体位移，以模拟地层的初始应力状态；然后进行盾构掘进施工，每次推进5个环宽(1.2 m)，即为6.0 m，分12步开挖完成，见图5. 隧道动态施工过程具体如下：① 开挖隧道内部的土体，每步开挖5环；② 为模拟盾构开挖面支护效应，在开挖面施加支护力0.30 MPa的分布荷载；③ 运行一定的时步后，释放隧洞边界地层应力25%[18]，以模拟盾尾的空隙引起的地层损失；④ 拼装衬砌管片，并进行盾尾壁后注浆，壁后注浆采用等代层来模拟；⑤ 等代层为水泥加强土体，对注浆圈外的地层施加0.25 MPa注浆压力；⑥ 求解计算；⑦ 进行下一步开挖计算，直至隧道全部开挖完成.

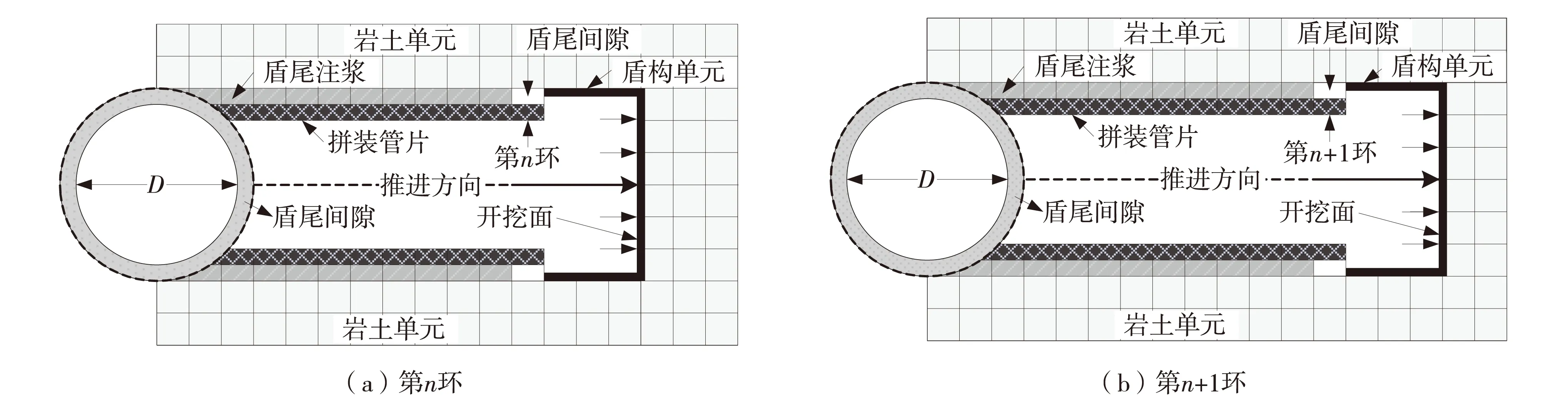
图5　盾构隧道动态掘进示意图Fig.5　Schematic diagram of shield tunneling

3.4变形监测点布设

取隧道推进方向y=36.0 m(断面Ⅲ)为横向监测断面，间隔3.0 m等间距布设监测点，研究不同深度位置横向地层变形动态变化规律；在监测断面Ⅲ上，设置A、B、C和D四个监测点，研究地层水平变形随深度方向变化规律；同时，在隧道中心正上方分别距地表0.8、4.8和8.8 m深度位置，并沿盾构推进方向间隔3.0 m等间距布设监测点，研究地层变形沿隧道纵向动态变化规律. 测点布置见图6.

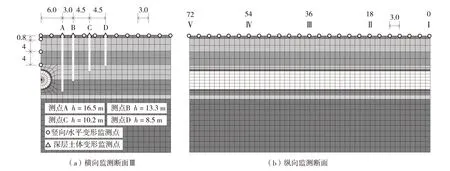
图6　监测断面及监测点布置(单位：m)Fig.6　Monitor points arrangement plan (unit: m)

4结果分析

4.1地层竖向变形规律

4.1.1横断面地层竖向变形

图7为盾构推进过程不同时步沿隧道横断面地表竖向变形曲线. 由图7可得，盾构推进第1、2、4、6、8和12时步，地表竖向变形最大值依次为-13.35、-16.57、-16.99、-17.02、-17.03和-17.04 mm，最终形成的地表竖向变形曲线与Peck公式计算值基本吻合；地表竖向变形随着盾构向前推进不断发展变化，形成的沉降槽宽度越来越大，沉降槽深度也越来越深，最后渐趋稳定.

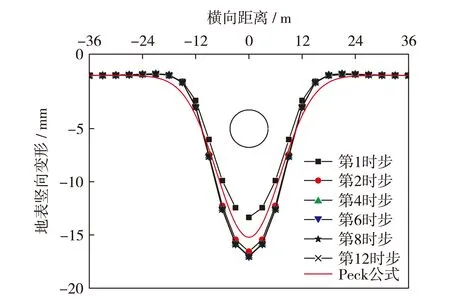
图7　不同时步地表竖向变形曲线Fig.7　(Color online) Curves of vertical deformations of ground for different time steps

不同深度位置沿隧道横断面地层竖向变形数值计算值与理论值对比如图8. 由图8可得，地表竖向变形数值计算值与采用本研究式(6)计算结果吻合较好；在地表下0、0.8、4.8和8.8 m不同位置，地层竖向变形最大值分别为-17.02、-17.46、-19.03和-22.14 mm；隧道开挖后，隧道周围土体向洞内逐渐移动，在隧道中心上方形成“V”形沉降槽，沉降槽宽度约为6D； 随着埋深的增加，沉降槽宽度逐渐减小，沉降值逐渐增大，即埋深越大，沉降曲线“窄高”型特征越明显，埋深越小，沉降曲线“矮胖”型特征越明显.

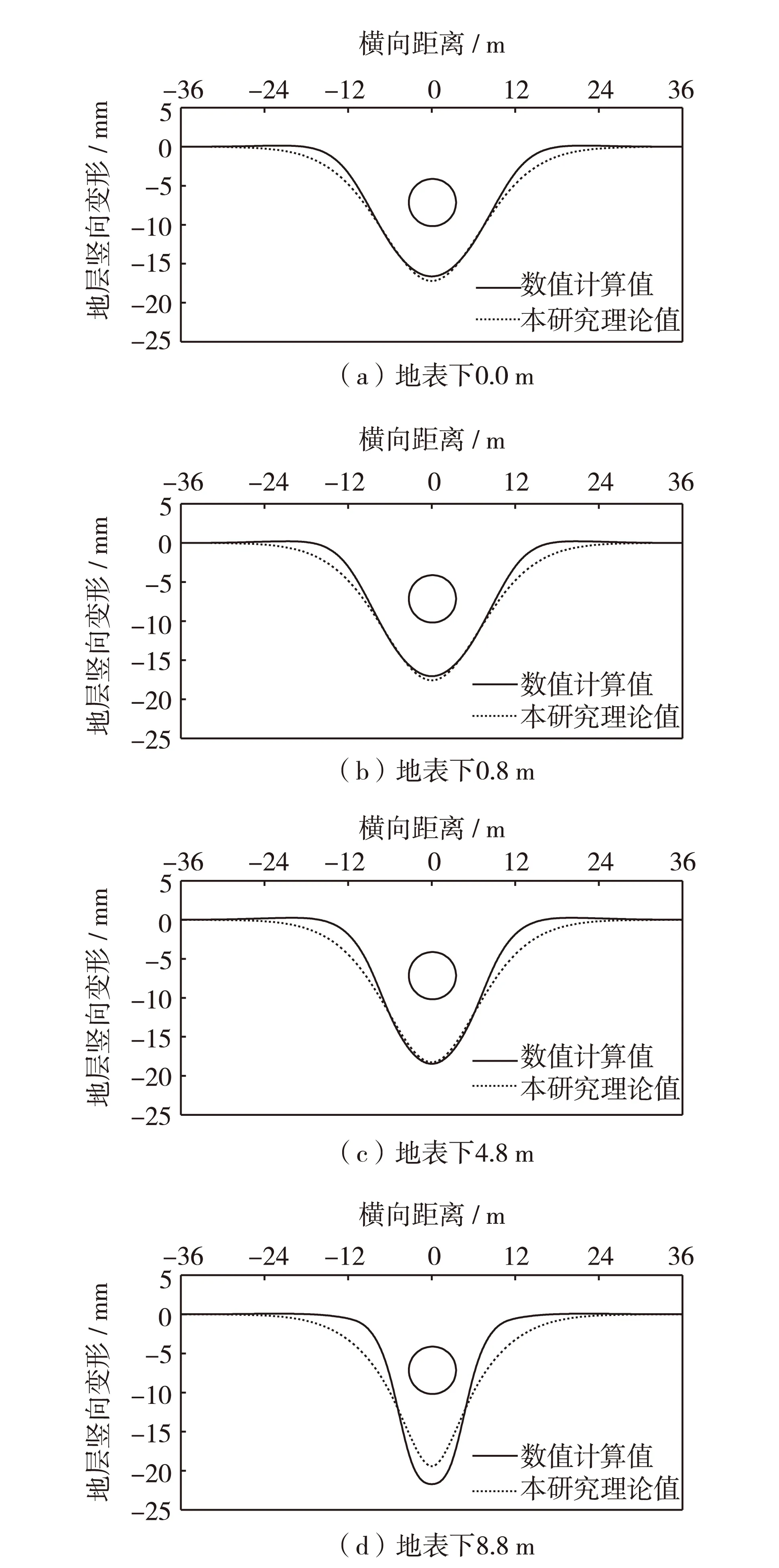
图8　不同深度处地层竖向变形曲线Fig.8　Curves of vertical deformations of stratum for different depths

4.1.2纵断面地层竖向变形

不同深度位置沿隧道轴线方向地层竖向变形数值计算值与理论值对比如图9所示. 由图9可得，在开挖面前方，隧道上部地层受到隧道周围土体的支撑及盾构推力的作用，地层表现为隆起；在开挖面后方，隧道内因土体开挖而脱空，土体逐渐向洞内移动表现为沉降；纵向地层变形呈倒“S”形分布，开挖面前后3D以外地层竖向变形逐渐趋于稳定，埋深越深，地层竖向变形值越大；数值试验值与本研究理论计算结果变化趋势较为接近，且数值试验过程中能考虑开挖面支护力、壁后注浆等施工因素.

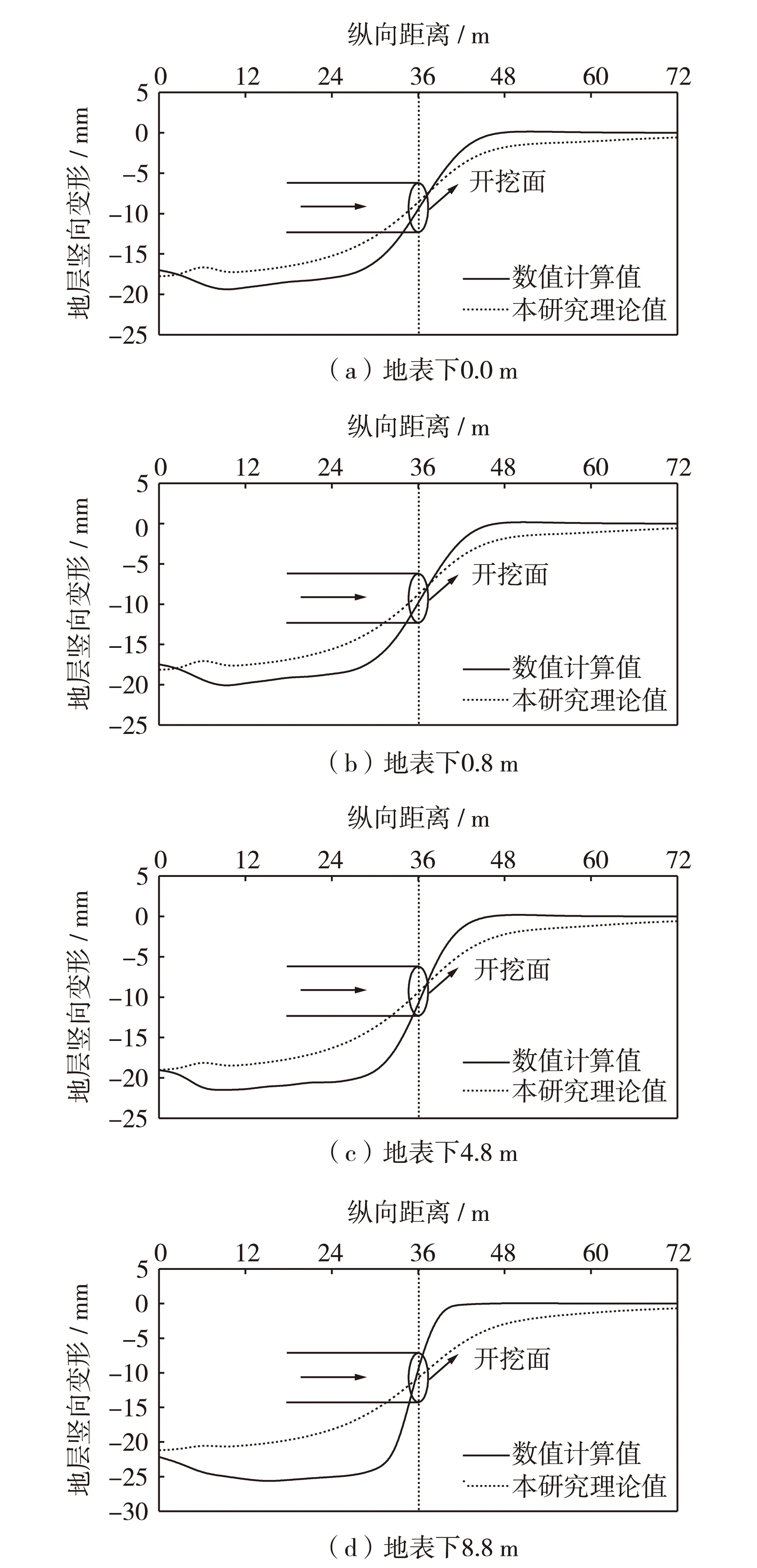
图9　地层竖向变形沿纵断面变化曲线Fig.9　Curves of vertical deformations of stratum with longitudinal section

4.2地层水平变形规律

4.2.1横断面地层水平变形

图10为盾构推进过程不同时步沿隧道横断面地层水平变形曲线. 由图10可得，盾构施工引起的地层水平变形左右两侧反对称；盾构推进第1、2、4、6、8和12时步，地表水平变形最大值依次为4.42、6.09、6.74、6.84、6.86和6.87 mm；地表水平变形随着盾构向前推进不断发展变化，水平变形值及扰动影响范围逐渐扩大，随着隧道的开挖和支护后地表水平变形逐渐趋于稳定.

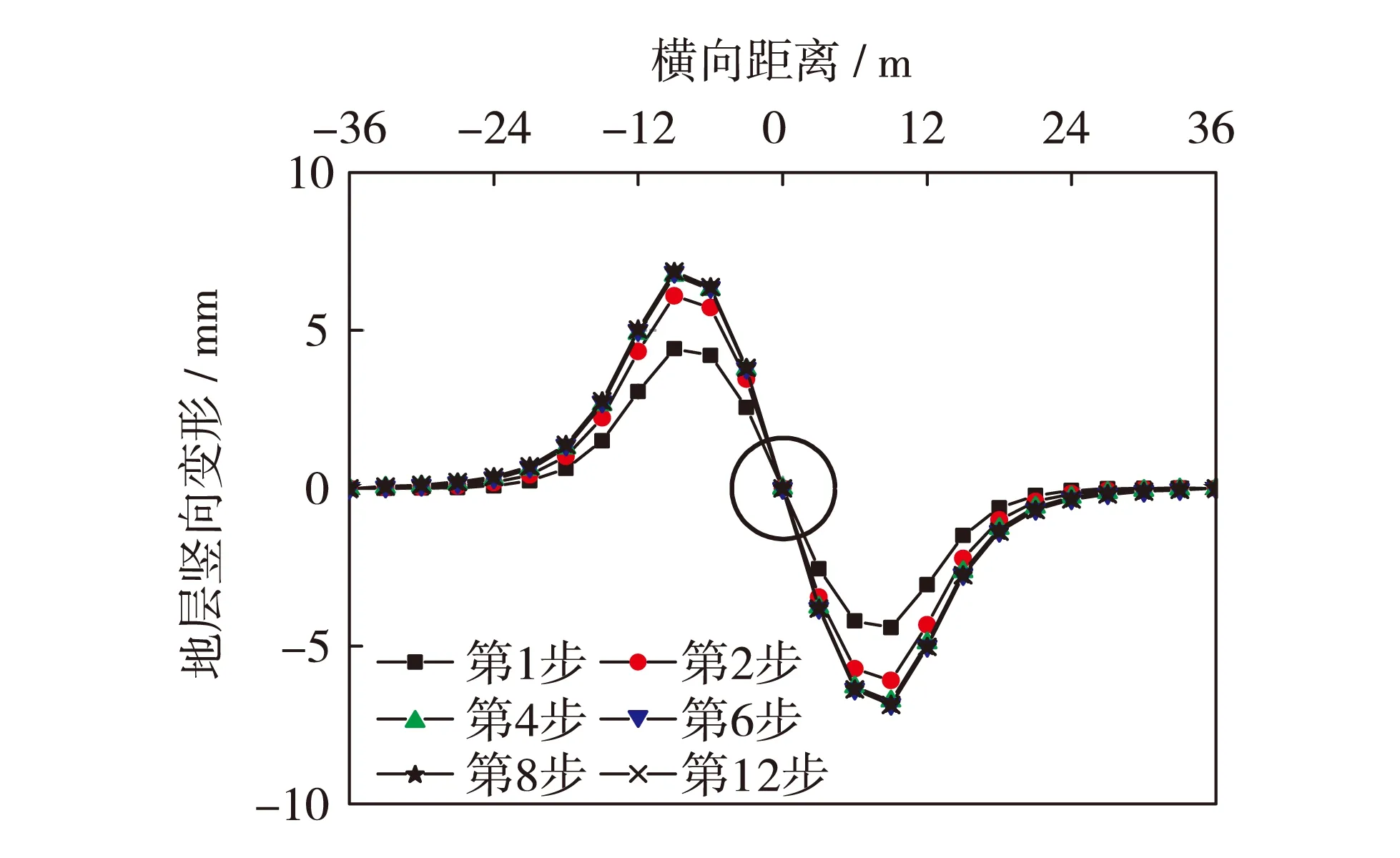
图10　不同时步横向地表水平变形曲线Fig.10　(Color online) Curves of horizontal deformations of ground for different time steps

不同深度位置沿隧道横断面地层水平变形曲线对比见图11. 由图11可得，地层水平变形左右两侧反对称，距隧道中心约D处地层水平变形值最大， 6D以外地层变形基本不受施工影响；随着埋深的增加，地层水平变形值减小，扰动影响范围也逐渐缩小；数值试验值与本研究理论计算结果变化趋势基本一致，但在埋深较大位置，理论值与数值试验结果略有差异，原因是理论方法仅考虑了地层损失的影响.

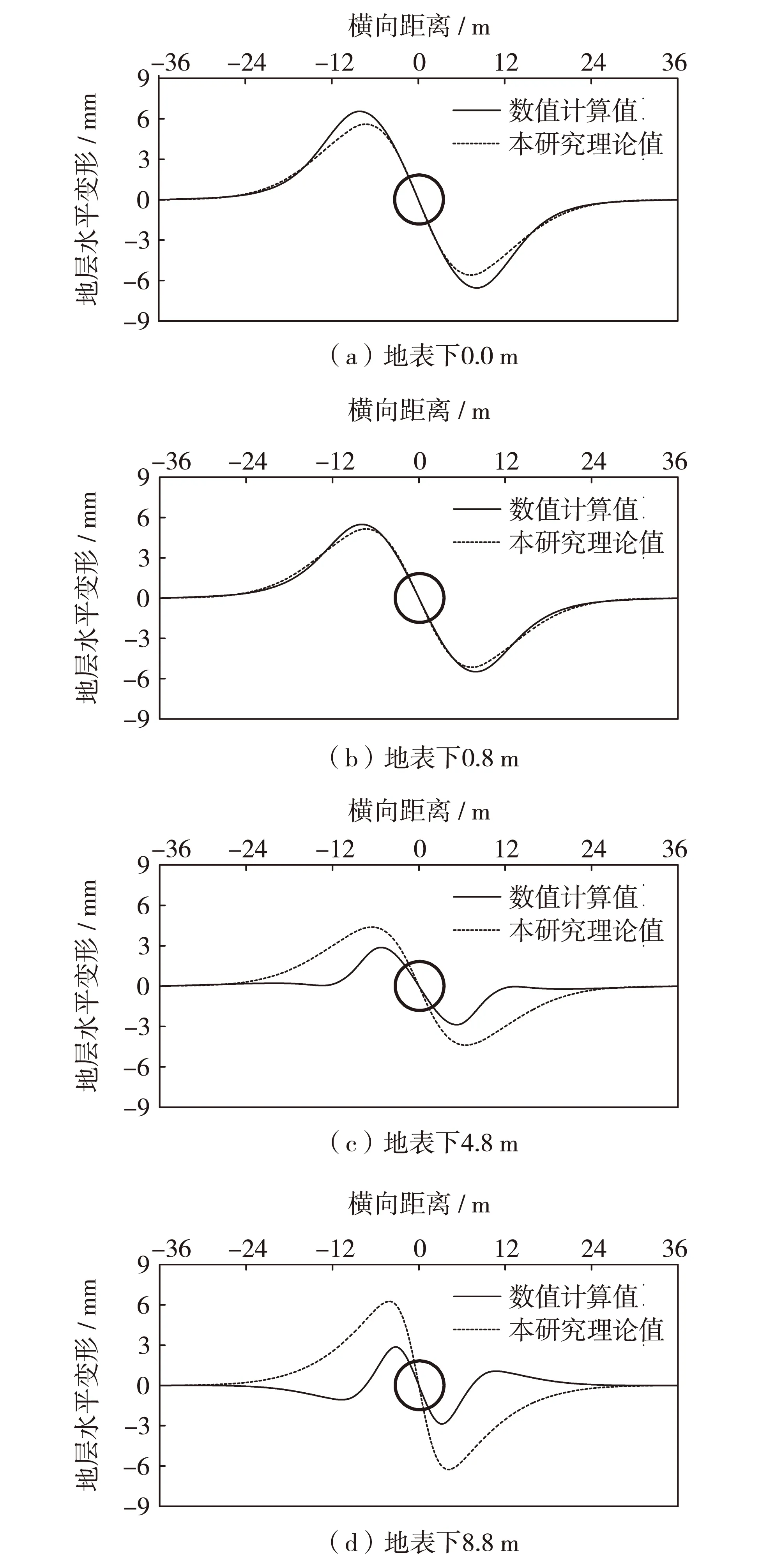
图11　不同深度横向地层水平变形曲线Fig.11　Curves of horizontal deformations of stratum for different depths

4.2.2深层土体水平变形

深层土体水平位移曲线对比如图12所示. 由图12可见，在同一深度，离隧道中心越近，地层水平变形受施工影响越大；测点D距隧道中心18.0 m，地表水平变形值为-1.06 mm，故距隧道中心3D以外地表水平变形受施工影响较小.

图12　深层土体水平变形曲线Fig.12　(Color online) Curves of horizontal deformations of soil for different depths

由水平变形数值试验值与理论计算结果对比可知，地层水平变形随深度变化趋势基本一致，但在隧道两侧土体水平移动方向相反. 其原因是数值试验过程中除考虑地层损失的影响外，还考虑了开挖面支护力、壁后注浆压力的影响，由于二力的作用使隧道左右两侧土体向外产生了移动，其值约为2.0 mm．本研究是基于地层损失理论基础上的地层变形预测方法，故未能反映此影响. 因此，在理论基础不完备的条件下，采用数值试验来模拟盾构施工地层移动和变形也不失为一种有效的手段，同时，基于盾构施工力学行为过程，建立能够考虑多因素的地层变形预测方法也是非常有必要的.

为进一步探讨深层土体水平变形规律，保持隧道计算半径R=3.2 m不变，取x=2.0R； h=1.5R、 2.0R、 2.5R、 3.0R、 4.0R、 6.0R、 8.0R和10.0R进行计算分析，计算结果见图13. 结果表明：① 隧道埋深越浅，地表水平变形值就越大；随着埋深的增加，深层土体水平位移最大值位置开始下移，并趋近于隧道的腰部； ② 当隧道埋深h≤2.0R时，水平位移曲线沿深度方向近似呈幂函数分布；当隧道埋深h≥8.0R时，水平位移曲线沿深度方向近似呈抛物线分布.

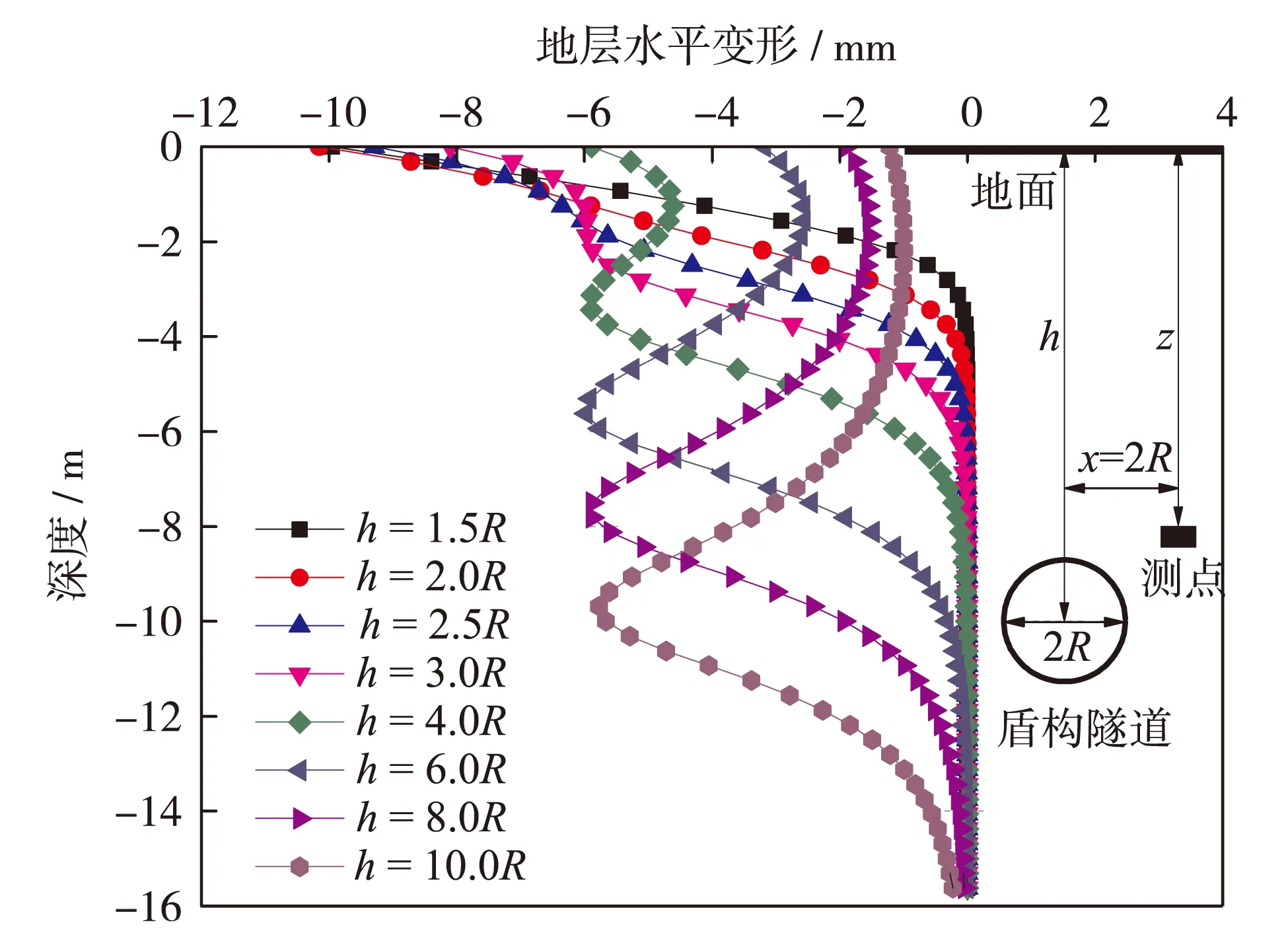
图13　深层土体水平变形比较Fig.13　(Color online) Comparison between horizontal deformations of soil for different depths

5结论

1)本研究理论计算方法能较好地反映盾构施工引起的地层变形特点，可用于盾构隧道设计与施工的前期计算分析；数值仿真能较好地再现盾构动态施工过程，计算结果与实测结果具有较高的一致性，可为盾构施工控制提供参考.

2)地层竖向变形沿隧道横断面呈“V”形沉降槽，沉降槽宽度约为6D， 地层深度越大，沉降槽宽度越小，沉降值越大；地层竖向变形沿隧道纵断面呈倒“S”形，开挖面前后3D以外地层竖向变形逐渐趋于稳定.

3)地层水平变形左右两侧反对称，距隧道中心约D处地层水平变形值最大， 6D以外地层变形基本不受施工影响，随着埋深的增加，地层水平变形值减小.

4)在同一深度，离隧道中心越近，地层水平变形受施工影响越大，距隧道中心3D以外地表水平变形几乎不受影响；隧道左右两侧土体受开挖面支护力和壁后注浆压力的挤压作用向外移动，水平变形值约为2.0 mm.

引文：邱明明，杨果林，姜安龙，等．地铁盾构施工地层变形预测及数值分析[J]. 深圳大学学报理工版，2016，33(4)：377-387.

参考文献/ References：

[1] 何川,封坤,方勇.盾构法修建地铁隧道的技术现状与展望[J].西南交通大学学报自然科学版,2015,50(1):97-109.

He Chuan, Feng Kun, Fang Yong. Review and prospects on constructing technologies of metro tunnels using shield tunnelling method. [J]. Journal of Southwest Jiaotong University Natural Science Edition, 2015,50(1):97-109.(in Chinese)

[2] 邱明明,姜安龙,舒勇.城市地铁盾构施工地层变形三维数值模拟分析[J].防灾减灾工程学报,2014,34(2):161-167.

Qiu Mingming, Jiang Anlong, Shu Yong. Three-dimensional numerical simulation analysis of stratum deformation induced by subway shield construction[J]. Journal of Disaster Prevention and Mitigation Engineering,2014,34(2):161-167.(in Chinese)

[3] Peck R B. Deep excavations and tunneling in soft ground[C]// Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico, Russia: [s.n.], 1969： 225-290.

[4] Attewell P B, Woodman J P. Predicting the dynamics of ground settlement and its derivatives caused by tunnelling in soil[J]. Ground Engineering,1982, 15(8):13-20.

[5] 陈春来,赵城丽,魏纲,等.基于Peck公式的双线盾构引起的土体沉降预测[J]. 岩土力学,2014,35(8):2212-2218.

Chen Chunlai, Zhao Chengli, Wei Gang, et al. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula[J]. Rock and Soil Mechanics, 2014,35(8): 2212-2218.(in Chinese)

[6] Sagaseta C. Analysis of undrained soil deformation due to ground loss[J].Geotechnique,1987,37(3):301-320.

[7] Verruijt A, Booker J R. Surface settlements due to deformation of a tunnel in an elastic half plane[J].Geotechnique,1996,46(4): 753-756.

[8] Loganathan N, Poulos H G. Analytical prediction for tunneling-induced ground movement in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846-856.

[9] Park K H. Elastic solution for tunneling-induced ground movements in clays[J]. International Journal of Geomechanics, 2004,4(4):310-318.

[10] Mirhabibi A，Soroush A. Effects of surface buildings on twin tunnelling-induced ground settlements[J]. Tunnelling and Underground Space Technology, 2012, 29: 40-51.

[11] 韩凯航,张成平,王梦恕.浅埋隧道围岩应力及位移的显式解析解[J].岩土工程学报,2014,36(12):2253-2259.

Han Kaihang, Zhang Chengping, Wang Mengshu. Explicit analytical solutions for stress and displacement of surrounding rock in shallow tunnels[J].Chinese Journal of Geotechnical Engineering,2014,36(12): 2253-2259.(in Chinese)

[12] 魏纲,张世民,齐静静,等.盾构隧道施工引起的地面变形计算方法研究[J].岩石力学和工程学报,2006,25(S1): 3317-3323.

Wei Gang, Zhang Shimin, Qi Jingjing, et al. Study on calculation method of ground deformation induced by shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(S1): 3317-3323.(in Chinese)

[13] 叶飞,苟长飞,陈治,等.盾构隧道同步注浆引起的地表变形分析[J].岩土工程学报,2014,36(4): 618-624.

Ye Fei, Gou Changfei, Chen Zhi, et al. Ground surface deformation caused by synchronous grouting of shield tunnels[J].Journal of Railway Engineering Society, 2014,36(4): 618-624.(in Chinese)

[14] Liu Baochen. Ground surface movement due to underground excavation in the P.R.China[J]. Comprehensive Rock Engineering, 1993(4): 780-816.

[15] Yang J S, Liu B C, Wang M C. Modeling of tunneling-induced ground surface movements using stochastic medium theory[J]. Tunnelling and Underground Space Technology, 2004, 19(2): 113-123.

[16] 谷拴成,李敏.西安地铁盾构施工地表沉降随机介质预测研究[J]. 铁道工程学报, 2014, 31(3): 110-116.

Gu Shuancheng, Li Min. Study and prediction of surface settlement in Xi’an subway during shield construction based on stochastic medium theory[J].Journal of Railway Engineering Society, 2014,31(3): 110-116.(in Chinese)

[17] 张云, 殷宗泽, 徐永福. 盾构法隧道引起的地表变形分析[J]. 岩石力学与工程学报, 2002, 21(3): 388-392.

Zhang Yun, Yin Zongze, Xu Yongfu. Analysis on three-dimensional ground surface deformations due to shield tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3): 388-392.(in Chinese)

[18] 张志强, 何川, 佘才高. 南京地铁盾构掘进施工的三维有限元仿真分析[J]. 铁道学报, 2005, 27(1): 84-89.

Zhang Zhiqiang, He Chuan, She Caigao. Three-dimensional finite element modeling of excavation and advancement processes of shield tunnel construction in Nanjing Metro[J]. Journal of the China Railway Society, 2005, 27(1): 84-89.(in Chinese)

[19] 王国才,马达君,杨阳,等.软土地层中地铁盾构施工引起地表沉降的三维有限元分析[J].岩土工程学报,2011, 33(1): 266-270.

Wang Guocai, Ma Dajun, Yang Yang, et al. 3D finite element analysis of ground settlement caused by shield construction of metro tunnels in soft soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 266-270.(in Chinese)

[20] Li Z L, Soga K, Wright P. Long-term performance of castiron tunnel cross passage in London clay[J]. Tunnelling and Underground Space Technology, 2015, 50: 152-170.

[21] Itasca Consulting Group. FLAC user manuals[M]. Minneapolis, USA:[s.n.], 2004.

[22] 彭文斌. FLAC实用教程[M]. 北京:机械出版社, 2011.

Peng Wenbin. FLAC practical tutorial[M]. Beijing: China Machine Press, 2011.(in Chinese)

[23] 任建喜,李庆园,郑赞赞,等.盾构诱发的地表及邻近建筑物变形规律研究[J].铁道工程学报,2014, 31(1): 69-74.

Ren Jianxi, Li Qingyuan, Zheng Zanzan, et al. Research on the deformation laws of surface and adjacent building induced by shield tunnel[J]. Journal of Railway Engineering Society,2014,31(1): 69-74.(in Chinese)

[24] 魏纲. 盾构隧道施工引起的土体损失率取值及分布研究[J]. 岩土工程学报, 2010, 32 (9): 1354-1361.

Wei Gang. Selection and distribution of ground loss ratio induced by shield tunnel construction[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1354-1361.(in Chinese)

[25] 龚晓南.土塑性力学[M].杭州:浙江大学出版社,1999.

Gong Xiaonan. Soil plasticity mechanics[M]. Hangzhou: Zhejiang University Press,1999.(in Chinese)

【中文责编：坪梓；英文责编：之聿】

中图分类号：U 455

文献标志码：A

doi：10.3724/SP.J.1249.2016.04377

基金项目：国家自然科学基金资助项目(51478484，51278499)；中央高校基本科研业务费专项基金资助项目(2016zzts063)

作者简介：邱明明(1985—)，男，中南大学博士研究生.研究方向：道路与铁道工程、隧道及地下工程力学行为及基础理论. E-mail: sxdfqiuming@163.com

Numerical analysis of stratum deformation induced by tunnel boring machine construction for metro

Qiu Mingming1, Yang Guolin1†, Jiang Anlong2, and Shen Quan1

1) School of Civil Engineering, Central South University, Changsha 410075, Hunan Province, P.R.China 2) Xiamen Rail Transit Group Limited Corporation, Xiamen 361001, Fujian Province, P.R.China

Abstract：On the basis of the case study of the subway tunnel by tunnel boring machine construction and adopting the finite difference software FLAC, we establish three-dimensional stratum-structure model to simulate the dynamic process of tunnel boring machine construction. We put forward an improved three-dimensional prediction method of stratum deformation caused by tunnel boring machine construction based on stratum loss theory. The horizontal and vertical deformations of stratum are analyzed and compared with theoretical results. The results indicate that transversal stratum vertical deformation induced by tunnel boring machine construction presents a V-shaped curve. The width of settlement tank is about six times the tunnel diameter. Longitudinal stratum vertical deformation induced by tunnel boring machine construction demonstrates a S-shaped curve. The front excavation surface is uplifted and the back excavation surface is settled. It is changed gradually stable when the distance is greater than three times the diameter from the excavation surface. The curves of stratum horizontal deformation are the anti-symmetrical distribution, the maximum horizontal deformation is happened at about one time the diameter from the tunnel center. About six times the diameter from the tunnel center will be not influenced by shield construction. With the buried depth of tunnel getting bigger, the deformation of stratum horizontal gets smaller and the soils of tunnel arch haunch move to outside of the hole. The conclusion can be used and referenced for the design and construction of subway tunnel.

Key words：tunneling engineering；subway; tunnel boring machine construction; ground loss; prediction model; stratum deformation; three-dimensional simulation; dynamic simulation

Received：2015-10-20；Accepted：2016-04-15

Foundation：National Natural Science Foundation of China (51478484, 51278499);Fundamental Research Funds for the Central Universities (2016zzts063)

† Corresponding author：Professor Yang Guolin. E-mail:guoling@mail.csu.edu.cn

Citation：Qiu Mingming, Yang Guolin, Jiang Anlong,et al. Numerical analysis of stratum deformation induced by tunnel boring machine construction for metro[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(4): 377-387.(in Chinese)

【土木建筑工程 / Architecture and Civil Engineering】