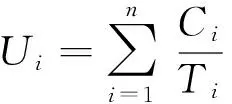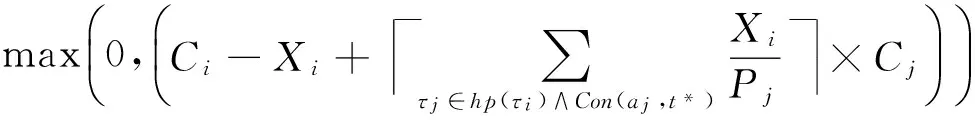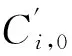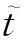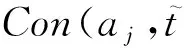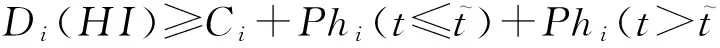截止时限为关键参数的混合关键级实时任务调度研究

黄丽达　　　李仁发

(湖南大学信息科学与工程学院　长沙　410082)



截止时限为关键参数的混合关键级实时任务调度研究

黄丽达李仁发

(湖南大学信息科学与工程学院长沙410082)

(hld_jt@hnu.edu.cn)

摘要混合关键级系统 (mixed criticality system)的研究源于在单一平台上执行多个重要级不同的功能,当前混合关键级调度研究，一般考虑高关键级任务在不同关键级运行模式表现为或周期或计算时间不同，即以任务释放时间间隔和最差情况执行时间为关键参数.但截至时限(dendline)也是实时任务的重要时间参数，尤其是对硬实时任务，以截止时限作为关键参数进行相应混合关键级调度的研究尚是空白.针对此问题，以截止时限作为关键参数，以响应时间分析为基础，对单处理器平台中的混和关键级任务的可调度性进行分析，并提出了一种预提升关键级的调度算法RCLA(raising critical-level in advance)，在低关键级运行模式下，高关键级低优先级任务有限度地提前抢占低关键级高优先级任务的执行，既确保了满足高关键级任务在不同关键级运行模式下的截止时限，也让尽可能多的任务可以被调度执行，使得计算资源得以充分利用.仿真结果验证了RCLA算法的有效性.

关键词混合关键级；实时调度；截止时限；关键参数；响应时间

嵌入式领域中，在单个共享的计算平台上执行具有不同功能的多个实时任务，已成为能够兼顾能耗、成本、散热等多方面需求的解决之道[1].混合关键级系统(mixed criticality system)正是此类系统中的典型代表[2].所谓混合关键级意味着在单一平台上同时执行多种功能(多种任务),其中某些任务比其他任务更为“重要”，例如汽车控制系统中防抱死制动系统的正确工作比车载收音机的正确工作要更关键，这里正确工作(或正确执行)的含义对于实时任务而言就是要满足其截止时限(deadline)[3].

在混合关键级系统中，待执行任务集里的各个任务按照关键程度会被分配相应的关键级，即相对更为重要的，或者对生命、重大财产的安全影响更大的任务就会有相对更高的关键级，称之为高关键级任务，反之则称为低关键级任务.运行中的混和关键级系统总是处于某一个关键级状态，此时不低于系统当前关键级的任务均可以被调度执行；当由于外界事件触发系统关键级提升时，相对于系统当前关键级更低的任务就不再保证其正确执行，换而言之不再保证满足其截止时限.混和关键级系统既实现了在同一物理平台上最大可能地利用资源，尽可能调度执行多种任务充分使用平台的计算能力，也总是能够满足高关键任务的时间截止时限，从而同时确保高资源利用率和高安全性.

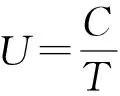
本文对混和关键级系统中不同关键级相应截止时限不同的待调度任务集模型进行定义，在单处理器平台上为了保证高关键级任务的截止时限在不同关键级执行总能被满足，基于固定优先级的响应时间分析，对以截止时限为关键参数的混和关键级系统的可调度性进行了分析，并提出了一种预关键级提升算法(raising critical-level in advance, RCLA)，分离任务被分配的优先级和关键级，具有低优先级的高关键级任务有限度地提前抢占具有高优先级的低关键级任务的执行，从而总能保证高关键级任务的截止时限，同时将对低关键级任务正确执行的影响控制在一个有限的范围内.

1任务模型与定义

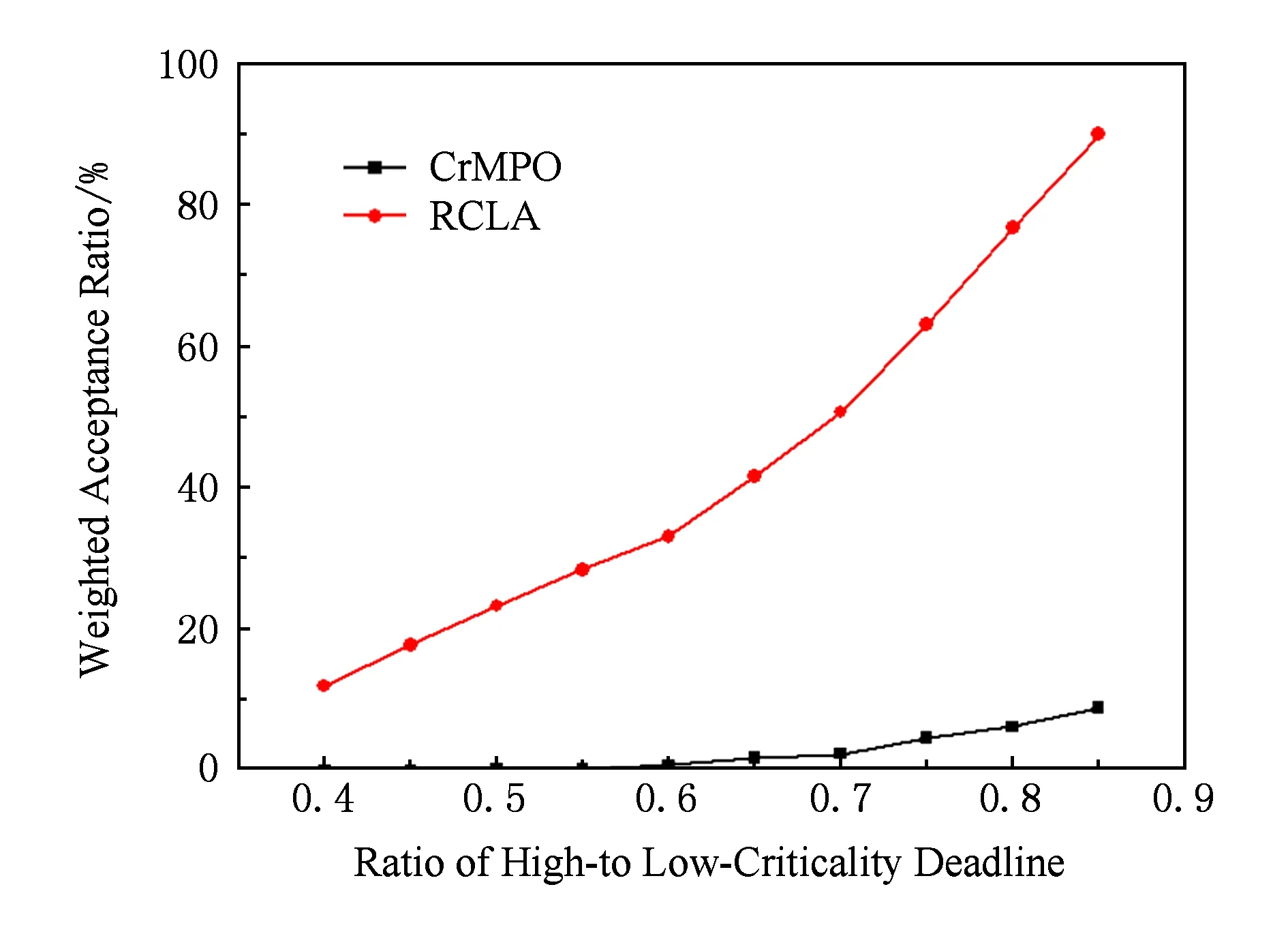
在单处理器平台上，待调度任务集τ由互不相关、允许抢占的有限个同步周期任务组成，τ={τ1,τ2,…,τn}，其中n表示任务个数.任务τi定义为τi(Ci,Pi,Di,li)，其中Ci是最差情况下的执行时间WCET；Pi是任务τi的周期；li表示任务τi的关键级属性；Di为一向量，表示不同关键级有不同截止时限值Di=(Di(L1),Di(L2),…,Di(Li))，L1表示系统最低关键级，通常是从数值1开始.为讨论方便，暂时仅考虑系统只有高低2个关键级的情况，即有τi(Ci,Pi,{Di(LO),Di(HI)},li)，若任务为低关键级任务(下文简称之为LO任务)，则li=LO且其截止时限Di(LO)=Di(HI)；若任务是高关键级任务(下文简称之为HI任务)，那么li=HI且其截止时限Di(LO)>Di(HI).∀i，Ci

定义1. 关键参数.实时任务的时间参数包括执行时间、周期、截止时限等，在混合关键级系统中，HI任务在不同系统关键级会有相应的不同时间参数，称这种对应不同关键级执行具有不同值的时间参数为关键参数.

定义2. 调度窗口.一个实时任务的调度窗口是指从其释放时间到其绝对截止时限的这一段时间间隔,其中绝对截止时限di=ai+Di.

系统处于不同关键级执行时，可调度执行的任务属性或者任务数量也会不同，这与文献[13]中模式的概念吻合，即称系统处于不同关键级模式.一般认为系统从低关键级模式开始执行，由于外界事件触发[14]，产生关键级提升，亦称为发生关键级切换，因此关键级提升时刻对于混和关键级系统本身是不能预先可知的.

在实际实时嵌入式应用中多使用固定优先级调度[15]，本文使用截止时限单一调度(deadline-monotonic, DM)算法对某一个系统关键级模式下的任务进行调度，使得所有任务均能在低关键级模式下被调度执行，HI任务在高关键级模式下均能被调度执行.

2截止时限作为关键参数的任务可调度性

如图1所示，a是HI任务τi的释放时刻，Ri是其响应时间，若时刻t*是系统由低关键级提升到高关键级的时刻，由于Di(HI)

Fig. 1　HI-task at the time of raising critical-level.图1　关键级提升时刻对任务的影响

1) 在时刻t*时，之前所释放的所有HI任务已经执行完毕，即Xi<0.此种情况下无需考虑HI任务由于系统关键级提升所受到的影响.在该调度窗口内继续执行完毕时刻t*时未执行完的LO任务.至少a+Pi后才进入高关键级模式调度.

2) 在时刻t*时，如果正在执行HI任务τi,即如图1所示情况，或者尚有HI任务没有执行完毕，那么就需要关注已经或正在执行的高优先级LO任务对相对低优先级的HI任务是否能满足提前的截止时限影响，即在时刻t*进入高关键级模式后，HI任务的相对截止时限提前，应分析是否HI任务在当前调度周期内可保证满足Di(HI)，即在(a+Di(HI)-t*)这一段时间内是否足以提供HI任务尚未完成的计算时间.

应用响应时间的概念[3]对上述情况1进行分析讨论.由于使用DM调度算法，那么任务τi的响应时间Ri可计算为

(1)

其中,hp(τi)表示优先级高于任务τi的任务集.由于相对截止时限是关键参数，所以由式(1)可知，任务响应时间的计算结果不受关键级变化的影响.

对于前述情况2进行2点讨论：

① 若ai+Di(HI)≥ai+Ri，那么在当前调度窗口[ai,ai+Di(HI))，正在执行的调度方案仍然有效，无需进行其他操作；

② 若ai+Di(HI)

Ci,0=

(2)

其中，条件Con(aj,t*)表示较高优先级任务τj的释放时间需满足aj>t*，即较高优先级任务在提升时刻t*之后还有释放.那么在系统处于低关键级运行模式时，已经开始执行的较低优先级的HI任务仍然可能在执行过程中被抢占.由此可得，HI任务τi未完成的执行时间可定义为

(3)

即，若满足：

(4)

那么就可以通过简单丢弃在Xi这段时间内将要执行的LO任务即可满足高关键级模式下的截止时限；若不满足式(4)，那么就需要从时刻t*前的高优先级LO任务“剥夺”计算时间，因为这些LO任务对于HI任务而言就是导致HI任务不能满足Di(HI)的干扰任务.

3预先提升关键级

若从关键级提升时刻之后无法获得足够的计算时间完成WCET，满足Di(HI)，可以从2种方案考虑保证HI任务调度问题：

方案1. 调整任务优先级分配方案.为防止LO任务被分配高优先级，从而对HI任务正确执行产生可能的干扰，总是先执行HI任务，即优先级与关键级一致.这样的调度方法实际已经退化成完全基于关键级的调度方案CrMPO[7]，对资源利用率的提升没有益处.

(5)

(6)

其中，Phi表示比任务τi优先级高的任务子集在任务τi执行完毕之前的执行时间，Phi由2部分组成：

(7)

(8)

(9)

Table 1　An Example of Mixed-Criticality Task Set

依据DM，表1中任务集的调度序列如图2所示:

Fig. 2　Scheduling in Low-Criticality with DM.图2　低关键级时使用DM调度任务集

如图2所示，在低关键级模式，任务优先级是按照DM进行分配，低关键级的任务τ2的优先级是最高的.设若关键级提升时刻以整数倍时间单元进行[16].以相对截止时限作为关键参数，对关键级提升的时刻分别进行讨论：

1) 若关键级提升发生在(5,8]期间，不满足式(4)，尚未执行完毕的高关键级任务τ1是没有办法满足其D1(HI)，解决方案只有预关键级提升.

2) 若关键级提升发生在(4,5]期间，对于HI任务τ2也无法满足式(4)，相应D2(HI)亦无法满足，解决方案只有预关键级提升.

3) 若在其它时刻进行关键级提升，对调度HI任务满足截止时限没有影响，无需考虑.

Fig. 3　Scheduling with RCLA.图3　使用预关键级提升的调度方案

依据图3所示调度方案，形成预关键级提升算法RCLA(raising critical-level in advanced)，算法表述如下：

算法1. 预关键级提升RCLA.

输入：有限个同步周期任务集τ={τ1,τ2,…,τn}，其中τi(Ci,Pi,{Di(LO),Di(HI)},li)；

输出：调度任务执行序列.

Step1. 按照DM排序待调度任务集τ={τ1,τ2,…,τn}，此时任务调度序列仅依据相对截止时限升序排列；

Step2. 根据式(1)计算HI任务的响应时间，若τi∈Γ∧li=HI，且Ri≤Di(HI)，则该高关键级任务无需提前执行；

Step5. 在最后一个执行的HI任务的响应时间之后，若没有发生系统关键级提升则继续依据DM顺序调度LO任务；否则进入高关键级运行模式，基于DM调度HI任务.

在待调度任务数目有限的情况下，由于响应时间分析的时间复杂度是伪多项式时间的，因此基于响应时间分析的RCLA算法的时间复杂度也是伪多项式时间的，若以z表示发生关键级提升时刻的调度窗口长度，那么RCLA算法的时间复杂度可表示为O(n2×z)，其中n为待调度任务数，即RCLA算法的时间复杂度是多项式时间的.

虽然在前文中，RCLA算法对于相对低和相对高的2种关键级任务进行讨论获得的，RCLA很容易被扩展到多于2级关键级的多关键级混合系统，且对跨关键级执行关键级提升的情况同样适用.

4仿真结果与分析

本节对以截止时限为关键参数的混合关键级系统使用RCAL算法调度任务集的有效性进行仿真评估.根据文献[17]，错过截止时限比率(miss deadline ration, MDR)是比较调度算法有效性的重要指标，即对相同待调度任务集满足截止时限的任务数目越多，则认为相应的调度算法更优.本文采用的评价指标为系统可接受任务比率(acceptance ration,A)，A=1-MDR=(满足截止时限的任务数)(任务集中待调度任务总数).

由于目前对混合关键级中以截止时限为关键参数的调度研究极少，在现有公开发表的文献中，以截止时限作为关键参数的混合关键级的调度至今仍是空白，使用CrMPO(criticality monotonic priority order)调度算法用作比对分析对象，并依据仿真结果讨论待调度任务集的特性对调度结果的影响.

仿真实验中用到的任务集参数按照5个过程随机生成：

2)设定最大执行时间Cmax，则Ci在{1,2,…,Cmax}范围内服从均匀分布随机生成；

4)Di(LO)=CF×Di(HI)，其中参数CF(criticality factor)为一个固定倍增数，由于Di(HI)

5) 随机生成任务li=HI，即为HI任务的可能性由参数CP确定，例如CP=0.5

仿真实验选取任务集利用率U∈[0.025,0.975]，步进间隔为0.025.每一个利用率值，生成任务数量为1 000个，选取Cmax=10.图4显示了在CP=0.5即有50%的任务为HI任务、每个HI任务的高关键级时截止时限是低关键级时截止时限的0.6倍即CF=0.6时，RCLA与CrMPO可调度任务比率随着任务利用率增长可接受任务比率的变化情况.由图4可知，使用RCLA算法，混和关键级的可接受任务数目，即可调度的任务数目远好于使用CrMPO，尤其是在轻负载，即利用率小于50%的情况下，使用RCLA可调度的任务数目平均比使用CrMPO的多出了4.8倍.

Fig. 4　Percentage of schedulable tasks.图4　可调度任务比率

下面我们研究调整参数CP和CF对可调度任务数目的影响.使用加权可调度任务比率(或称之加权可接受任务比率)[19]作为以前述可调整参数为变量的函数,加权可调度任务比率

(10)

其中,p是可变参数;y表示某一种可调度性算法;Sy(τ,p)是当参数值为p时使用调度算法y任务集τ的可调度性，其为1或0的二元值.使用加权可调度任务比例，可以降低问题的维度[17]，还可以覆盖到更大的利用率的值.

图5所示为随着HI任务的数目增加，即参数CP值增加，对可调度任务比率的影响.图6所示为随着参数CF值增加，即D(HI)与D(LO)逐渐接近时，对可调度任务比率的影响，总体上看，RCLA可调度的任务数目均优于CrMPO.

Fig. 5　The number of high criticality tasks affecting schedulable tasks.图5　HI任务数目对可调度任务比率的影响

Fig. 6　Varying CF affecting schedulable tasks.图6　不同参数CF对可调度任务比率的影响

不论随着HI任务比率的增加，还是D(HI)与D(LO)差异增加，从实验数据看，二者对于RCAL的影响相当，当HI任务超过一半，或D(HI)D(LO)<0.6，可调度任务集中基本上包含的LO任务已经不足13%，且可调度HI任务数目几乎是呈直线下降趋势，即调度成功的难度会大大增加.

5结束语

相对截止时限是实时任务最关键的时间参数之一，尤其对硬实时任务而言.在混合关键级系统中，很多时候高关键级任务需要被更紧急地正确执行，即高关键级时的截止时限相较于低关键级时的截止时限更小，即截止时限是混和关键级系统的关键参数.但据现有公开发表的文献，从提出混合关键级系统概念至今，关键级之间以任务计算时间或周期为关键参数的混合关键级系统调度算法被研究的较多，但是以(相对)截止时限作为关键参数的混合关键级系统的调度则被研究的极少.本文针对混和关键级调度需求，在单处理器平台，基于固定优先级，针对作为关键参数的截止时限的特点，对以截止时限为关键参数的混和关键级任务调度进行了任务建模，应用响应需求时间分析，进行了以截止时限为关键参数的混和关键级可调度分析，并提出了预关键级提升算法，使得在不同系统关键级下以及在关键级切换期间，高关键级任务的截止时限总能得到保证，同时尽可能让更多的低关键级任务得以执行，保证了平台计算资源安全、高效地使用，实验评估结果提供了良好的佐证.

在多处理器平台下，尤其是在允许任务在不同处理器之间迁移时，保证截止时限的情况更加复杂，尤其在混合关键级系统运行在多处理器平台时，计算能力得到提升，若没有良好调度算法的支持，高关键任务的正确执行并不会得到相应的保证，这是我们后续将继续研究的问题.

参考文献

[1]Homan D. Designing future systems for airworthiness certification[OL]. 2009[2012-01-19]. http:www.cse.wustl.edu～cdgillCPSWEEK09 MCARMCAR%20overview%20BoF%20CPS%20PA%20approved.pdf

[2]Vestal S. Preemptive scheduling of multi-criticality systems with varying degrees of execution time assurance[C]Proc of IEEE RTSS 2007. Piscataway, NJ: IEEE, 2007: 239-243

[3]Liu J. Real-Time Systems[M]. Upper Saddle River, NJ: Prentice-Hall, 2000

[4]Niz D D, Lakshmanan K, Rajkumar R. On the scheduling of mixed-criticality real-time task sets[C]Proc of IEEE RTSS 2009. Piscataway, NJ: IEEE, 2009: 291-300

[5]Baruah S, Li H, Stougie L. Towards the design of certifiable mixed-criticality systems[C]Proc of IEEE RTAS 2010. Piscataway, NJ: IEEE, 2010: 13-22

[6]Sebastian M, Axer P, Ernst R, et al. Efficient reliability and safety analysis for mixed-criticality embedded systems, PB 2011-01-0445 [R]. Detroit, Michigan: SAE Internatinal, 2011

[7]Guan N, Ekberg P, Stigge M, et al. Improving the scheduling of certifiable mixed-criticality sporadic task systems, PB 2013-008 [R]. Uppsala, Sweden: Department of Information Technology, Uppsala University, 2013

[8]Baruah S, Burns A. Fixed-priority scheduling of dual-criticality systems[C]Proc of the 21st ACM Int Conf on Real-Time Networks and Systems. New York: ACM, 2013: 173-181

[9]Fleming T. Extending mixed criticality scheduling [D]. York, UK: Department of Computer Science, University of York, 2013

[10]Hsiung P A, Lin C Y. Synthesis of real-time embedded software with local and global deadlines[C]Proc of the 1st IEEEACMIFIP Int Conf on HardwareSoftware Codesign and System Synthesis. New York: ACM, 2003: 114-119

[11]Burns A, Davis R. Mixed criticality systems—a review[R]. York, UK: Department of Computer Science, University of York, 2013

[12]Baruah S, Burns A. Implementing mixed criticality systems in Ada[C]Proc of the 16th Int Conf on Reliable Software Technologies. Edinburgh, UK: Ada-Europe, 2011: 174-188

[13]Real J, Crespo A. Mode change protocols for real-time systems: A survey and a new proposal[J]. Real-Time Systems, 2004, 26(2): 161-197

[14]Ng C K, Vyas S, Cytron R K, et al. Scheduling challenges in mixed critical real-time heterogeneous computing platforms[J]. Procedia Computer Science, 2013, 18: 1891-1898

[15]Baruah S, Pruhs K. Open problems in real-time scheduling[J]. Journal of Scheduling, 2010, 13(6): 577-582

[16]Ekberg P, Yi W. Bounding and shaping the demand of generalized mixed-criticality sporadic task systems[J]. Real-Time Systems, 2014, 50(1): 48-86

[17]Xiong M, Ramamritham K. Deriving deadlines and periods for real-time update transactions[J]. IEEE Trans on Computers, 2004, 53(5): 567--583

[18]Bini E, Buttazzo G C. Measuring the performance of schedulabilitytests[J]. Real-Time Systems, 2005, 30(12): 129-154

[19]Bastoni A, Brandenburg B, Anderson J. Cache-related preemption and migration delays: Empirical approximation and impact on schedulability[C]Proc of OSPERT 2010. Sankt Augustin, North Rhine-Westphalia, Germany: Euromicro, 2010: 33-44

Huang Lida, born in 1978. PhD candidate and lecturer at Hunan University. Her main research interests include real-time scheduling and embedded software.

Li Renfa, born in 1956. Professor and PhD supervisor at Hunan University. His main research interests include computer architecture and computer application technology.

收稿日期：2015-04-29；修回日期：2015-10-19

基金项目：国家自然科学基金项目(61173036)

中图法分类号TP316.2

Scheduling of Mixed Criticality Real-Time Tasks Set with Deadline as the Critical Parameter

Huang Lida and Li Renfa

(CollegeofComputerScienceandElectronicEngineering,HunanUniversity,Changsha410082)

AbstractAn increasing trend in real-time systems is to integrate multiple functionalities of different levels of criticality, or importance, on the same platform, which leads the research of mixed criticality systems. In the current mixed criticality scheduling research, worst-case execution times or periods of high critical-level tasks are critical parameters, which are different between in high-critical mode and low-critical mode. Deadline is also an important time-parameter, especially in hard real-time systems, whereas how to schedule mixed criticality tasks using deadline as the critical parameter is still lack of discussion. This paper considers the mixed criticality scheduling in which deadlines of tasks are the critical parameter on a uniprocessor platform. Towards satisfying schedulability of high-criticality tasks in both modes, we use response time analysis to get timing-demand of fixed priority tasks and propose the raising critical-level in advance (RCLA) scheduling algorithm. RCLA gets high-critical tasks with lower priority to preempt low-critical tasks with higher priority earlier and limitedly. As well as meeting the deadlines of high criticality tasks in high-criticality mode and low-criticality mode, RCLA can schedule mixed criticality tasks as many as possible. Simulation results illustrate the benefits of this scheme.

Key wordsmixed criticality; real-time scheduling; deadline; critical parameter; response time

This work was supported by the National Natural Science Foundation of China (61173036).