梯形加减速算法在伺服系统中的应用研究

李庆华

(中国电子科技集团公司第五十四研究所,河北 石家庄050081)



梯形加减速算法在伺服系统中的应用研究

李庆华

(中国电子科技集团公司第五十四研究所,河北 石家庄050081)

摘要伺服系统中经常出现大角度调转需求和追踪问题。典型PI算法在大角度调转时会出现严重的超调和振荡，因此要采取梯形加减速等改进算法来改善系统性能。分析了一种典型梯形加减速算法的原理，通过仿真和实际系统试验验证其效果，指出该算法对追踪问题具有的局限性，并提出了二次位置追踪算法和位置-速度追踪算法这2种减小局限性的方法。通过实际系统验证，证明改进方法有效。

关键词伺服系统；PI；梯形加减速；位置-速度追踪算法

0引言

在跟踪快速机动目标的应用场合，对伺服系统的快速性和稳定性要求很高。目前伺服系统一般采用PI算法[1]，对于连续位置指令可以快速高精度响应，但是对于大角度调转情形，由于积分饱和效应，会引起大的超调和多次振荡，产生的冲击会减小设备的寿命并可能造成安全隐患。尽管可以采取积分分离等改进措施，效果仍然不理想。

梯形加减速算法是根据误差按指定加速度调节速度指令，因此速度是连续的，尽管加速度的不连续也会造成冲击，但相对系统规模而言冲击较小，算法简单和响应快的优势却使得其适用性很强。

在一个3.7 m天线系统中采用梯形加减速算法验证其效果，大角度调转时天线可以平稳快速地指向目标位置，没有超调和振荡。但在给定斜坡函数即速度阶跃时，产生了系统不稳定、稳态有差等一系列问题。本文就这些问题进行分析，并给出解决方法。

1梯形加减速算法原理

1.1一类伺服系统的特征

伺服系统的通用化要求不外乎稳定、快速和准确地随动目标[2]。但是，根据目标特性的不同和天线伺服系统规模的大小，伺服系统也会对上述3个指标有所侧重。

机动目标没有确定轨道，在近场时，相对地面天线其速度快、加速度大，对伺服系统的快速性要求很高。实际的工作中需要各种操作模式，有利用引导使天线进入主波束后切入跟踪，有跟踪、引导随时人工切换，等等。这就要求天线在追踪(引导状态)时能够快速平稳地跟上引导值，各种方式切换时能够平稳无超调和振荡。本文的目的是找出一种能够支持大角度调转(静态及低速下的大角差引导)及追踪(快速下的大角差引导)方法并验证其实效。

1.2典型梯形加减速伺算法原理

梯形加减速算法用作大角度调转时对系统速度、加速度的控制。其运动过程为：运动起始，天线以给定加速度加速运动，当天线速度达到设定值后保持匀速运动；在此期间实时计算是否到达如下位置，即从该位置起，以给定加速度减速运动，到达目标点时天线速度减为零；从上述位置减速运动，到达目标点。

大角度调转时的运动包括匀加速段、恒速段和匀减速段3部分[3]，速度曲线呈梯形。在文献[4-6]中均指出，当调转距离短时，可能没有恒速段。此时速度曲线呈三角形[7]。

为简化算法，实际操作中采用速度-位置自适应算法：设定一个小的误差门限，当天线位置距离目标位置较远，即误差大于门限时采用位置开环的速度控制，当调转接近完成时误差小于门限，转入位置闭环，利用PI算法提高控制精度。

2梯形加减速算法改进及其在伺服系统中的应用

2.1典型加减速控制存在的问题

上述典型加减速控制是针对大角度调转问题的，在实际操作中没有任何问题。比如在一个3.7 m天线系统，设定最大速度35°/s，最大加速度20°/s2，分别给定10°和70°阶跃时，仿真的调转曲线如图1和图2所示。

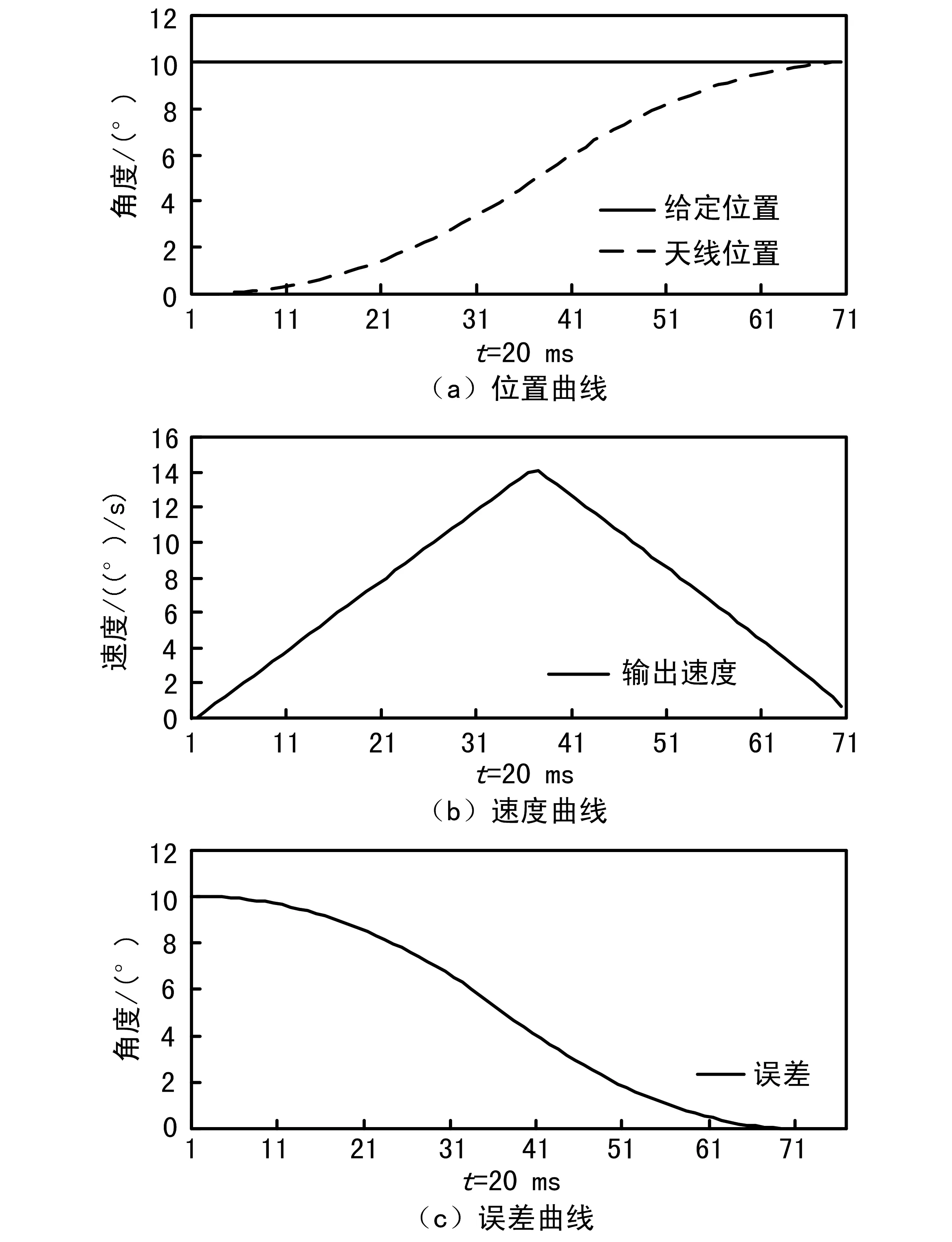
图1　10°阶跃调转曲线

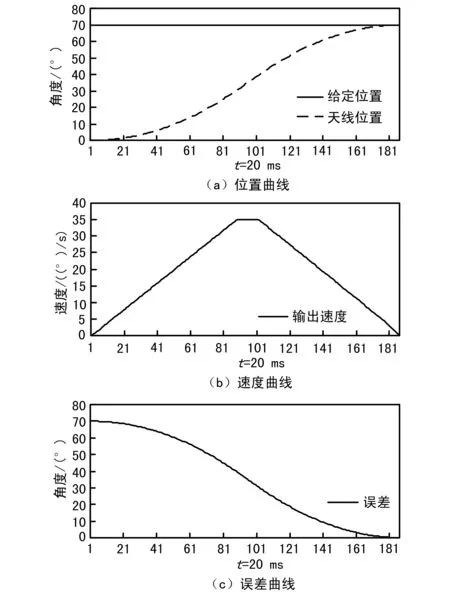
图2　70°阶跃调转曲线

由图1和图2可以看出，10°阶跃时由于调转行程小，没有恒速段，速度曲线呈三角形；70°阶跃时速度曲线则是典型的梯形，但是天线都能很快通过加速—减速过程平稳地调整到指定位置，没有超调。

但是，当给定斜坡函数即速度阶跃时，如设定10°/s的等速运动，天线很快调整进入到稳态，显示转速确实正确，但是显示偏差却不是零，而是一个常量，具有重复性，如图3所示。二型伺服系统对给定斜坡函数应该是稳态无差的，但给定的等速值又远远没有达到系统最大值，那么，这个偏差是哪里来的？

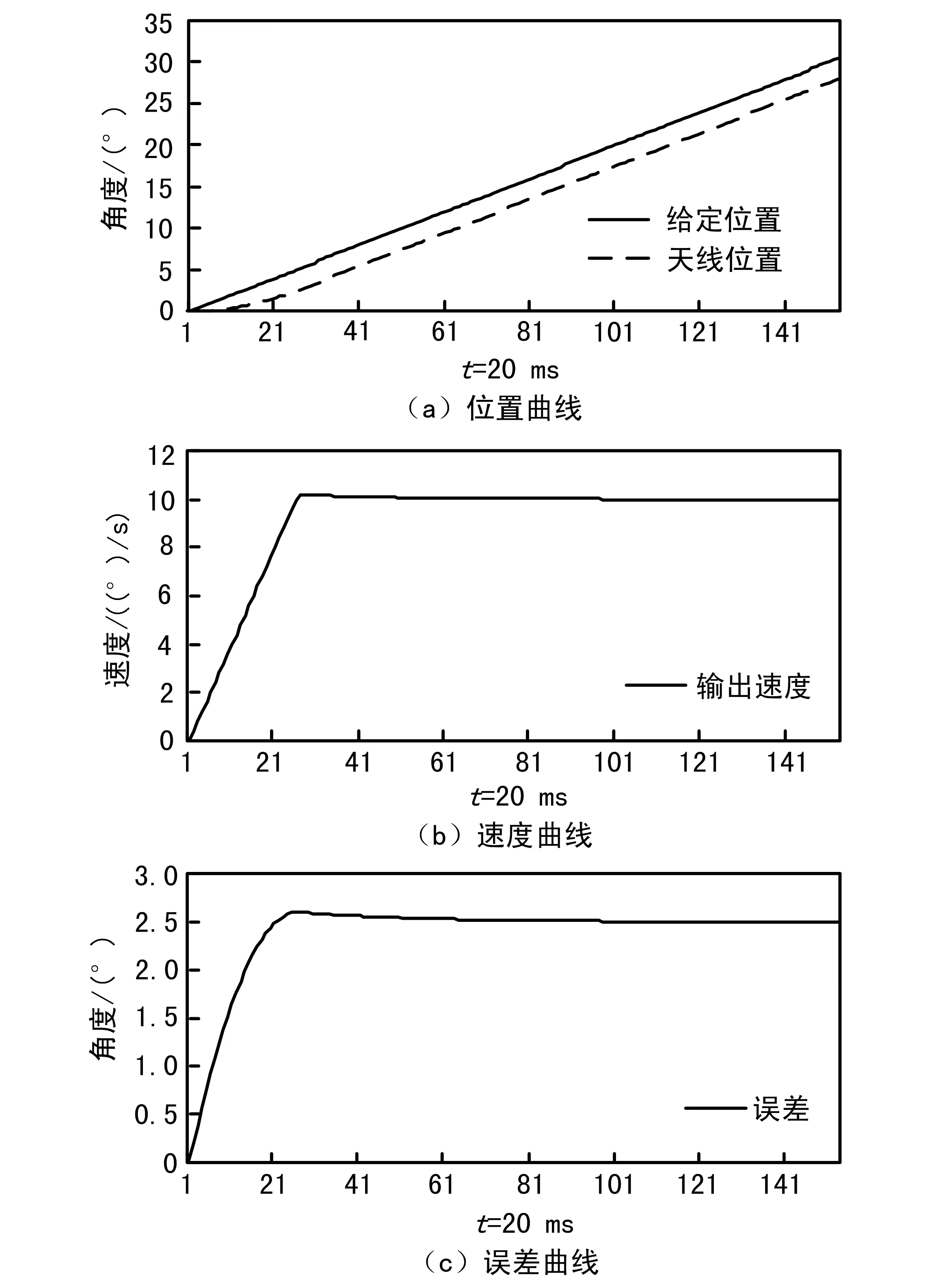
图3　10°/s速度阶跃调转曲线

经过仔细观察和分析，确认是调整没有进入位置闭环状态，也就是说稳态时误差大于闭环门限，伺服处于开环状态。将闭环门限向上调整，又出现2种现象：当闭环门限大于值后，调整可以进入位置闭环状态，只是闭环初期有抖动；当闭环门限在某值附近时，天线以极大概率进入不稳定状态，抖动剧烈。

经过分析可以得到一个结论：在减速段，当大于闭环门限的某一误差对应产生的速度恰好等于给定速度时，调整将进入稳态。因为不能位置闭环，此时误差将保留。如果调整给定速度，偏差也将随之变化，给定速度越大，这个偏差也越大。当给定速度对应的误差小于但接近闭环门限时，可以进入闭环状态，由于此时闭环算法中的积分项为零，天线仅以比例项运动，若相应速度小于给定转速，将导致误差加大而退出闭环门限，从而重新开始梯形加减速控制，由此产生振荡。

2.22次位置追踪算法

为实现大角度调转的平稳性，现在假设闭环门限取一个比较小的值，这样问题归结为：如何使天线逼近目标和如何平稳进入闭环。

仍然观察上述有差追踪过程。进入稳态后算法输出维持了与目标相同的速度，如果此时把该输出保存起来，例如保存在积分项，将输出清零，总输出改为算法输出和积分项相加，那么天线仍维持与目标同速。由于此刻天线与目标相对静止，把这种状态视作另一次大角度调转，调整后的状态应该是位置上追踪上目标，速度与目标相同(虽然第2次的大角度调转速度减为零，但此时的速度指令保存在积分项中)。此时进行位置闭环，由于积分项已经有维持目标速度的指令，比例项因为误差小(闭环门限很小)所以也很小，切换过程将十分平稳，这样通过2次梯形加减速控制实现了对斜坡函数的追踪。

2.3位置-速度追踪算法

2次位置追踪算法尽管可以实现对斜坡函数输入的跟踪，但是有些繁琐，调整过程也比较长。可以通过以下方法简化调整过程。

将原梯形加减速控制对象由追踪目标位置改为同时追踪目标位置和速度，这样当天线跟上目标时天线的转速和目标速度相同，此时进行闭环效果同前述算法。

给定误差和速度，对各种可能出现的情况进行仿真分析，证明该算法结果正确。仍然以10°/s的速度阶跃为例，从闭环原点开始施加阶跃，天线追踪的曲线如图4所示。从距离40°的位置施加反向阶跃，天线迎头赶上的调整过程如图5所示。2种情况最后天线都调整到位置、速度均与给定相同。

该算法的关键在目标速度的准确获取，流程比较简单，此处不再赘述。

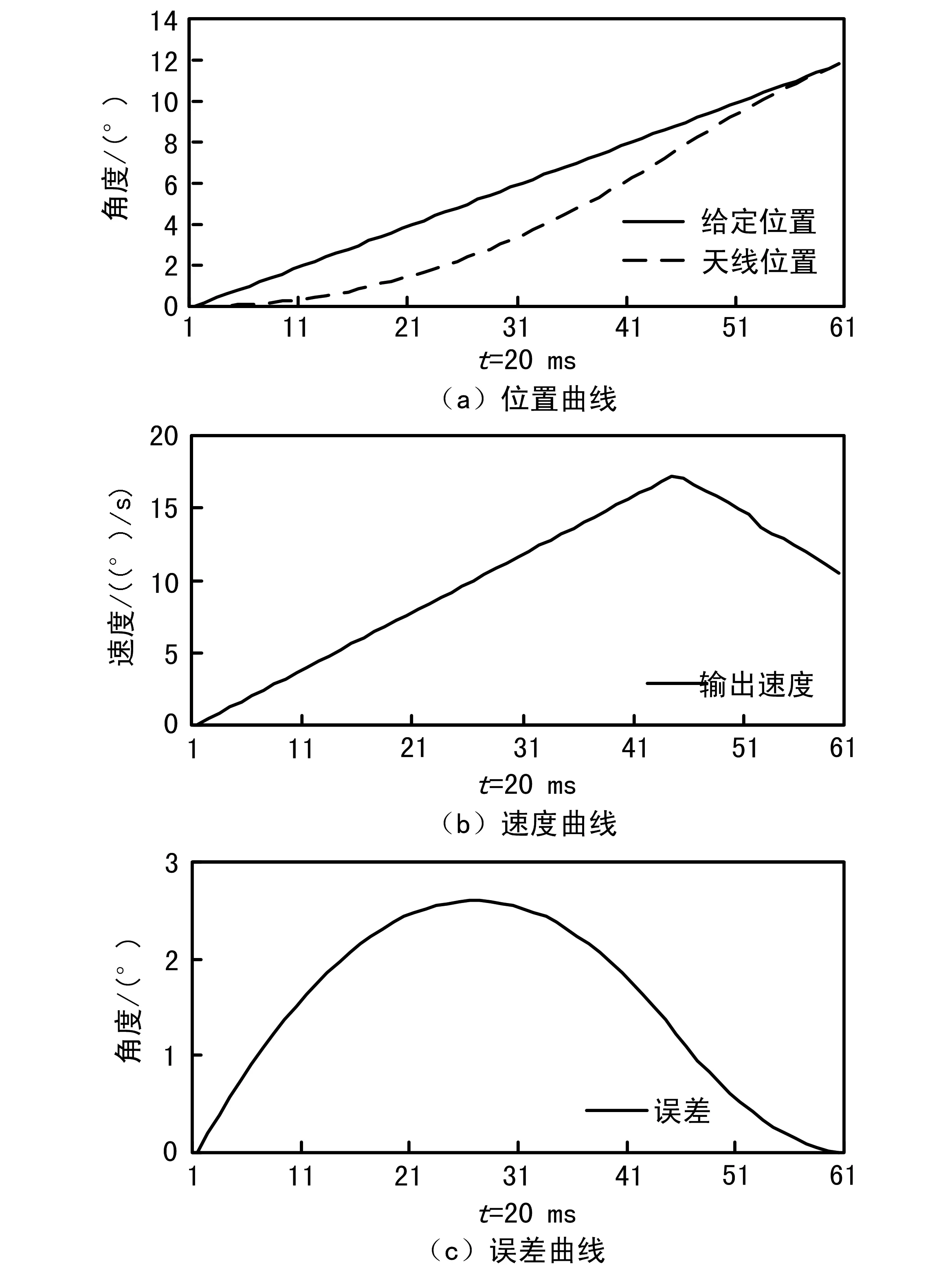
图4　10°/s速度阶跃位置-速度追踪曲线

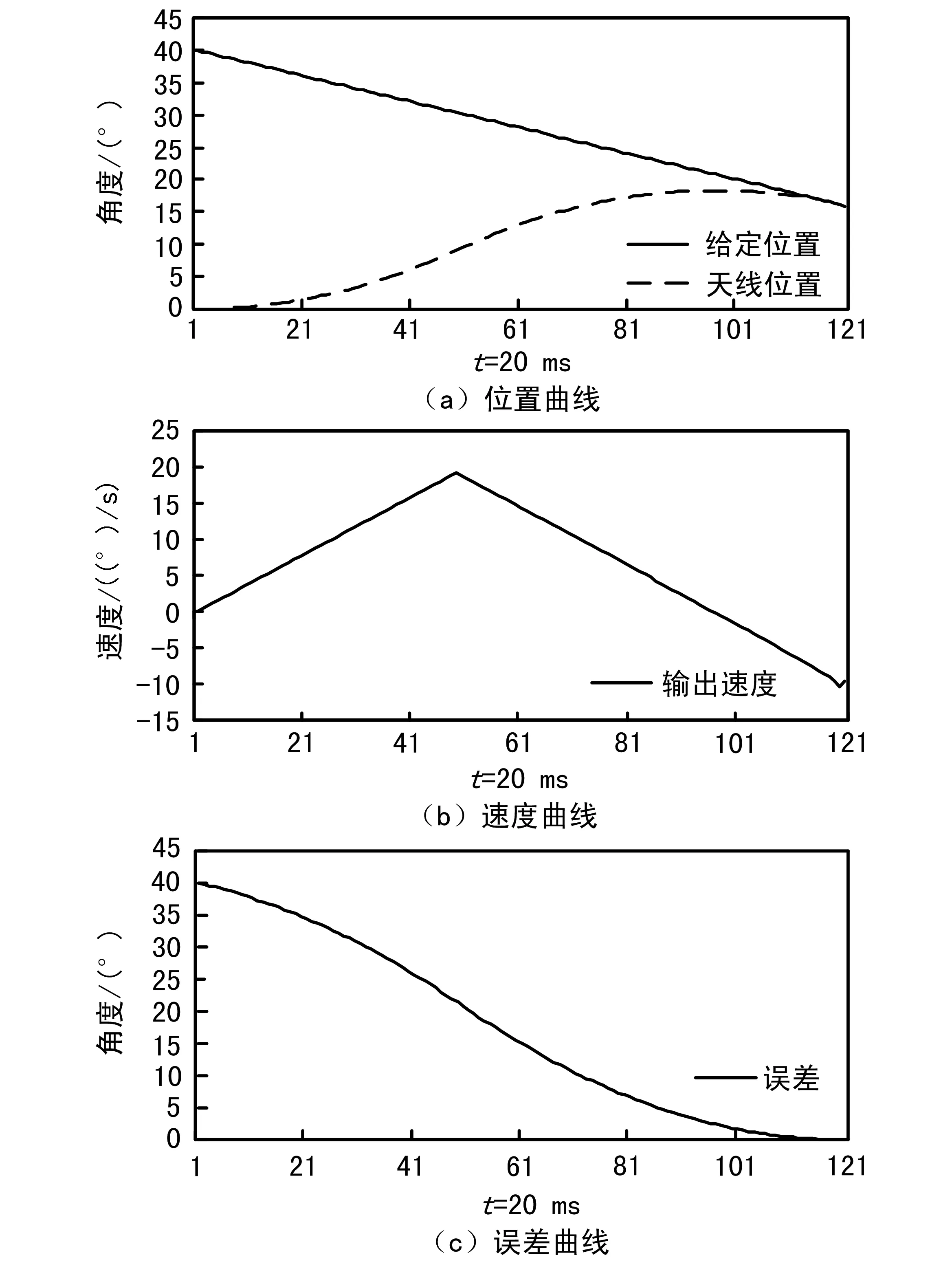
图5　10°/s反向速度阶跃位置-速度追踪曲线

3结束语

大角度调转和动态追踪等情况下，常规PI校正带来快速性和稳定性的矛盾，直观表现就是大超调和多次振荡。通过仿真证明，在典型梯形加减速算法的基础上，采用位置-速度追踪算法可以有效解决该问题，并且可以满足斜坡函数给定情况下的应用。经过在一套3.7 m天线系统上反复试验验证，该算法稳定可靠，试验结果与仿真结论相符。在试验中，采用了对输入量的跟踪-微分滤波器(TD)算法来近似获得目标速度量，当然也可以利用其他手段来获得目标速度量。相对于指数算法、S曲线算法等，该算法运算量要小得多，对于以低成本嵌入式处理器为控制器的系统，该算法有推广价值。

参考文献

[1]韩京清.自抗扰控制技术[M].北京：国防工业出版社，2008.

[2]胡寿松.自动控制原理[M].北京：科学出版社，2007.

[3]吴基斌.运动控制关键算法及嵌入式实现研究[D].广州：华南理工大学，2010.

[4]马志建.车载定向天线稳定跟踪平台的研究与开发[D].济南：山东科技大学，2009.

[5]赵明峰.基于PLCopen的运动功能模块的建模与实现[D].武汉：华中科技大学，2013.

[6]许鑫.嵌入式点胶控制系统研究与实现[D].武汉：华中科技大学，2014.

[7]严乐乐.基于DSP的运动控制器的软件开发[D].南京：南京航空航天大学，2007.

doi:10.3969/j.issn.1003-3106.2016.07.15

收稿日期：2016-03-31

基金项目：国家部委基金资助项目。

中图分类号TP202+.5

文献标志码A

文章编号1003-3106(2016)07-0056-04

作者简介

李庆华男，(1973—)，工程师。主要研究方向：自动控制。

Research on Application of Trapezium Ac/De Algorithm in Servo System

LI Qing-hua

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

AbstractThe large-angle rotation requirement and tracing problem often exist in conventional servo system.The typical PI algorithm may lead to large overshoot and vibration,so the improved algorithms are required to improve system performance,such as trapezium acceleration and deceleration(Ac/De).This paper analyzes the principle for the trapezium Ac/De algorithm,validates the effect of the algorithm by simulation and actual system testing,and indicates the limitations in tracing.Two methods are presented to reduce the limitation,Twice-Position Tracing algorithm and Position-Velocity Tracing algorithm.The test results for practical system show that this improved is available.

Key wordsservo system;PI;trapezium acceleration and deceleration;position-velocity tracing algorithm

引用格式：李庆华.梯形加减速算法在伺服系统中的应用研究[J].无线电工程,2016,46(7):56-59.