罕遇地震作用下高速铁路减隔震简支梁桥合理计算模型的探讨

卢　皓

(1.中铁第一勘察设计院集团有限公司，西安　710043；2.同济大学桥梁工程系，上海　200092)



罕遇地震作用下高速铁路减隔震简支梁桥合理计算模型的探讨

卢皓1，2

(1.中铁第一勘察设计院集团有限公司，西安710043；2.同济大学桥梁工程系，上海200092)

摘要：以往在分析减隔震桥梁的地震响应时，由于考虑到桥墩和基础应保持弹性工作状态，在基于强度的设计中偏于安全考虑桥墩一般采用毛截面刚度建立弹性梁单元模型。实际上，在罕遇地震作用下，桥墩墩底截面虽然未达到屈服状态，仍然会出现保护层混凝土开裂，并导致桥墩刚度降低。此时，应考虑对桥墩刚度进行适当修正以估计桥梁的各项地震响应参数，这也有利于实现减隔震桥梁基于位移的抗震设计。结合西部高速铁路中典型的简支梁桥结构形式，分别采用弹塑性纤维梁柱单元、弹性梁柱单元、考虑刚度修正的弹性梁柱单元模拟桥墩建立3种计算模型，探讨适用于罕遇地震作用下的高速铁路减隔震桥梁的合理计算模型。结果表明，当罕遇地震作用下桥墩位移延性超过0.5时，考虑刚度修正的弹性梁柱单元模拟桥墩的计算模型能够较好地估计桥梁各项地震响应参数。

关键词：高速铁路；简支梁桥；减隔震；计算模型；弹塑性纤维梁柱单元；非线性时程分析

高速铁路(客运专线)在建设中大量采用了“以桥代路”，据统计，桥梁比例已达到高速铁路线路总长度的70%～80%以上，而其中绝大部分都是简支箱梁桥[1]。因此，高速铁路桥梁抗震设计应重点研究解决简支箱梁桥所存在的问题。为了满足列车高速运行中的安全性和舒适度，高速铁路的桥墩以及支座必须有足够的刚度，在此基础上需要进一步保证高速铁路桥梁的抗震性能，中铁第一勘察设计院集团有针对性的研发了一种减震装置减震榫[2-3]。减震榫实际上是一种低屈服点软钢阻尼器，设置于梁部结构和桥墩之间，是弯曲型的金属阻尼器。该装置能够实现“支座功能分离”的设计理念，在地震作用下将塑性变形集中于减震榫，而桥墩及基础仍处于弹性工作状态，因此大幅度提高了结构的抗震性能。

对于传统铁路桥梁以及安装减隔震装置的铁路桥梁的地震响应和抗震性能研究已经有大量的研究成果[4-7]。以往在计算减隔震桥梁的地震响应时，由于考虑到桥墩和基础应保持弹性工作状态，因此桥墩一般采用毛截面刚度建立弹性单元模型，只将塑性变形控制在减隔震装置上。而在罕遇地震作用下，安装了减隔震装置的桥梁，桥墩墩底截面虽然未达到屈服状态，也发生了保护层混凝土的开裂，使得刚度降低，这在桥墩较高时尤为明显，此时，若仍采用毛截面刚度建立弹性单元模型将会对计算结果产生偏差，宜考虑在该模型上对桥墩刚度进行适当的修正。本文将以弹塑性纤维单元建立桥墩的有限元模型为基准，选取了7条II类场地强震记录作为地震输入进行非线性时程分析，探讨弹性单元模型以及修正刚度后的弹性单元模型在分析罕遇地震作用下高速铁路减隔震桥梁地震响应的适用性。

1工程背景及减隔震装置介绍

1.1计算模型

以宝兰(宝鸡—兰州)客专的无砟轨道后张法预应力混凝土48 m简支箱梁为例，箱梁构造和桥墩构造见图1(a)，其中梁体混凝土强度等级为C50。桥墩形式选择适用范围在墩高3～20 m的圆端形桥墩，桥墩构造见图1(b)，根据施工图设计的配筋情况可知，圆端形桥墩墩底截面的配筋率达到了0.9%。其中桥墩混凝土强度等级为C40，二期恒载按照160 kN/m设计。

图1　箱梁及桥墩构造(单位：cm)

1.2减震榫介绍

中铁第一勘察设计院集团有限公司联合北京交通大学及中船重工七二五研究所，依托国家“八六三”课题，研制成功了具有减、隔震功能的减震榫，并通过了试验验证，减震榫构造见图2。

图2　单个减震榫构造(单位：mm)

减震榫采用“支座功能分离”的构思，将传统支座的水平力传递和竖向支承功能完全分离，梁体竖向反力及梁端转角仍由支座实现，水平力及水平位移由采用低屈服点钢阻尼器减震榫支撑和控制。本文计算分析时，选用的850A型减震榫的滞回曲线特征值见表1。

由表1中可以看到，随着减震榫设计位移的增加，屈后刚度和对应设计位移的割线刚度在不断降低，而阻尼比和屈服荷载在不断增加，屈后刚度和屈前刚度之比也在不断降低。可见，不同设计位移对应的等效刚度和屈服强度并不同，而这两个参数会极大影响减隔震桥梁的地震响应，因此，选用减震榫的减、隔震设计是一个迭代的过程。

表1　850A型减震榫滞回曲线特征值

2计算模型及地震动输入

2.1计算模型

以宝兰客专简支箱梁为例，针对无砟轨道48 m预应力混凝土简支箱梁，采用圆端形实体桥墩(适用墩高范围3～20 m)，建立了10、15、20 m 3种不同墩高的桥墩计算模型。为了考虑边界联的影响，建立了3跨简支梁模型，最后取P1和P2桥墩及中间跨简支梁的计算结果。限于篇幅，本文只讨论了该类桥在纵桥向地震作用下的地震响应，计算简图见图3。

图3　计算模型(单位：m)

主梁采用三维弹性梁单元模拟，单元质量堆聚在单元两端节点。混凝土结构的阻尼比取5%的Rayleigh阻尼，由于场地为Ⅱ类场地，墩底假设为固结，不考虑土-结构的相互作用。

在考虑桥墩的模拟时，采用了以下3种计算模型，计算模型1将桥墩采用弹塑性纤维梁柱单元模拟；计算模型2将桥墩采用弹性梁柱单元模拟；计算模型3将桥墩采用修正刚度的弹性梁柱单元模拟，以第1种计算模型的计算结果为基准验证其他2种计算模型的适用性。

计算模型1中，桥墩模拟采用Taucer等人提出的基于柔度法的弹塑性梁柱单元(分布塑性单元)[8]，该单元将钢筋和混凝土离散为纤维，假设纤维之间完全粘结，且满足平截面假定。弹塑性纤维梁柱单元的非线性特性由纤维的非线性应力-应变关系(材料非线性)来表示，混凝土本构关系用Mander模型模拟[9]。钢筋应力-应变关系采用Giuffré-Menegotto-Pinto模型来模拟[10]。

减震榫的恢复力计算模型是进行桥梁结构减震体系非线性地震反应分析的基础，国内外大量试验表明软钢阻尼器的滞回曲线都可以用双线性模型表示[11]，见图3(b)。若能够确定减震榫的设计位移，减震榫的计算模型可选用Wen[12]提出的弹塑性连接单元模拟减震榫的非线性力学行为，本文的有限元分析采用SeismoStruct程序完成。

2.2桥墩刚度的修正

通过对宝兰客专实体桥墩建立弹塑性纤维梁柱单元进行pushover分析，可以得到桥墩刚度KP，i的变化规律，将对应不同位移延性下的高速铁路实体桥墩割线刚度(弹塑性纤维模型)与弹性刚度的比绘制在图4中。

图4　高速铁路实体桥墩刚度变化规律

从图4可以看出，随着位移延性的增加，相比弹性刚度，桥墩刚度不断下降，呈现了幂函数的下降规律。并且，当位移延性超过0.5以后，桥墩的刚度与对应屈服状态的割线刚度差别不大。因此，在计算模型3中将桥墩采用修正刚度的弹性梁柱单元模拟时，采用对应屈服状态的等效刚度代替毛截面刚度，计算公式可直接采用《城市桥梁抗震设计规范》(CJJ166—2011)的建议公式[13]

(1)

2.3地震波的挑选

以《铁路工程抗震设计规范》[14]中定义的Ⅱ类场地、8度罕遇地震、水平地震基本加速度为0.57g、特征周期0.4 s的5%阻尼比设计反应谱为目标反应谱进行强震记录的选择和调整。所选地震波为远场且无明显脉冲特征。

本文先按照吕红山(2007)对中美两国场地分类指标的比较找出的联系[15]，从美国太平洋地震工程中心(PEER)的强震数据库NGA-West2中挑选Ⅱ类场地远场地震波，选取的强震记录中的PGA≥0.1g，无明显脉冲特征，震级在6～8级。然后在其中选择7条Drms小于0.04的强震记录，尽量避免从一次地震中选择过多记录，这7条波选自6次地震，最大可用周期均超过4 s。Drms是Ambraseys(2004)和Bommer&Acevedo (2003)[16，17]提出的用于验证所选择强震记录反应谱与设计反应谱的谱形匹配程度的一个指标。具体公式见相关文献，这里不再冗述。选取的7条强震记录列在表2中。

表2　强震记录

对以上强震记录调整至与目标谱一致的PGA=0.57g的强度水平，并采用SeismoMatch软件采用小波调整技术对线性调整后的母波进一步予以调整，调整范围从0～2 s，最大偏差控制在30%以内。将线性调整和小波调整后的强震记录加速度谱和设计反应谱绘制在图5中。

图5　加速度反应谱

由图5可知，在2.0 s以内的周期范围内，按照与反应谱谱形一致的原则从PEER NGA数据库挑选出来的7条强震记录，在只采用线性调整后的平均谱频谱特性与设计反应谱较为一致，2.0～4.0 s周期范围内强震记录平均谱和设计反应谱的偏差较大，这与《铁路工程抗震设计规范》(GB 50111—2009)对2 s以后长周期范围内的反应谱规定较为保守有关。而即使安装了减震榫，48 m高速铁路简支梁的基阶周期也不会超过2 s。

3数据分析及计算模型适用性探讨

以下将采用调整后的表2中的7条波作为地震动输入对3种计算模型进行非线性时程分析，计算结果取7条波的平均值。针对罕遇地震作用下墩底剪力、墩底弯矩、墩顶位移、减震榫变形这4项地震响应参数来讨论减隔震铁路桥梁的合理计算模型。限于篇幅，只讨论纵桥向地震作用下的地震响应。

考虑刚度要求和桥墩不进入屈服状态(能力需求比大于1，即墩底屈服弯矩与墩底弯矩地震响应之比大于1)的要求，经过迭代计算，得到10 m墩高简支梁的1孔梁可以安装32根、20根、16根减震榫，减震榫设计位移分别对应30、40、50 mm；15 m墩高简支梁的1孔梁可以安装22根、18根、14根减震榫，减震榫设计位移分别对应50、60、70 mm；20 m墩高简支梁的1孔梁可以安装18根、16根、14根减震榫，减震设计位移分别对应40、50、60 mm，模态分析结果见表3。

3.1墩底剪力计算结果分析

将采用3种计算模型得到的罕遇地震作用下墩底剪力地震响应结果列在图6中。

表3　安装减隔震装置的48 m简支梁桥的模态分析结果

由图6可知，在计算10 m墩高的48 m简支梁模型的墩底剪力地震响应时，弹塑性纤维梁柱单元和考虑桥墩刚度修正以及不考虑桥墩刚度修正的弹性梁柱单元模型的墩底剪力计算结果基本一致，误差控制在5%以内。随着墩高的增加，相比弹塑性纤维单元模型，未考虑桥墩刚度修正的弹性梁柱单元模型的计算结果明显偏大。而考虑了桥墩刚度修正的弹性梁柱单元模型的计算结果误差较小，在计算15 m墩高计算模型和20 m墩高计算模型的墩底剪力地震响应时，误差都控制在5%以内。

3.2墩底弯矩计算结果分析

将采用3种计算模型得到的罕遇地震作用下墩底弯矩地震响应结果列于图7。

图6　3种计算模型的墩底剪力地震响应比较

图7　3种计算模型的墩底弯矩地震响应比较

由图7可知，在计算10 m墩高的48 m简支梁模型的墩底弯矩地震响应时，3种计算模型的墩底弯矩地震响应计算结果基本一致，而考虑桥墩刚度修正的弹性梁柱单元模型的计算结果更为接近弹塑性纤维梁柱单元模型，误差最大为7%(减震榫设计位移为40 mm的情况)。而随着墩高的增加，相比弹塑性纤维单元模型，未考虑桥墩刚度修正的弹性梁柱单元模型的计算结果明显偏大，而考虑桥墩刚度修正的弹性梁柱单元模型的计算结果略小。采用修正刚度的模型在计算墩高15 m的48 m简支梁桥的墩底弯矩地震响应时，误差控制在5%以内，在计算墩高20 m的48 m简支梁桥的墩底弯矩地震响应时，误差最大出现在减震榫设计位移为50 mm时，误差为14%。

3.3墩顶位移计算结果分析

将采用3种计算模型得到的罕遇地震作用下墩顶位移地震响应结果列于图8。

由图8可知，3种计算模型在计算墩顶位移地震响应时，相比弹塑性纤维单元模型，未考虑桥墩刚度修正的弹性梁柱单元模型的计算结果明显偏小，误差基本达到了65%。而考虑桥墩刚度修正的弹性梁柱单元模型的计算结果与弹塑性纤维单元模型较为接近，只在计算10 m墩高计算模型时误差较大，而在计算15 m和20 m墩高计算模型的墩顶位移地震响应时，误差基本控制在30%以内。这是由于10 m墩高的简支梁桥在安装了减震榫后，且考虑减震榫设计位移为30、40、50 mm时，墩顶位移延性分别为0.56、0.37、0.29，考虑刚度折减的计算模型适用于桥墩位移延性超过0.5的情况，因此在10 m墩高计算模型的墩顶位移地震响应分析时，考虑刚度折减产生的结果偏大。

3.4减震榫变形计算结果分析

将采用3种计算模型得到的罕遇地震作用下减震榫变形地震响应结果列于图9。

图8　3种计算模型的墩顶位移地震响应比较

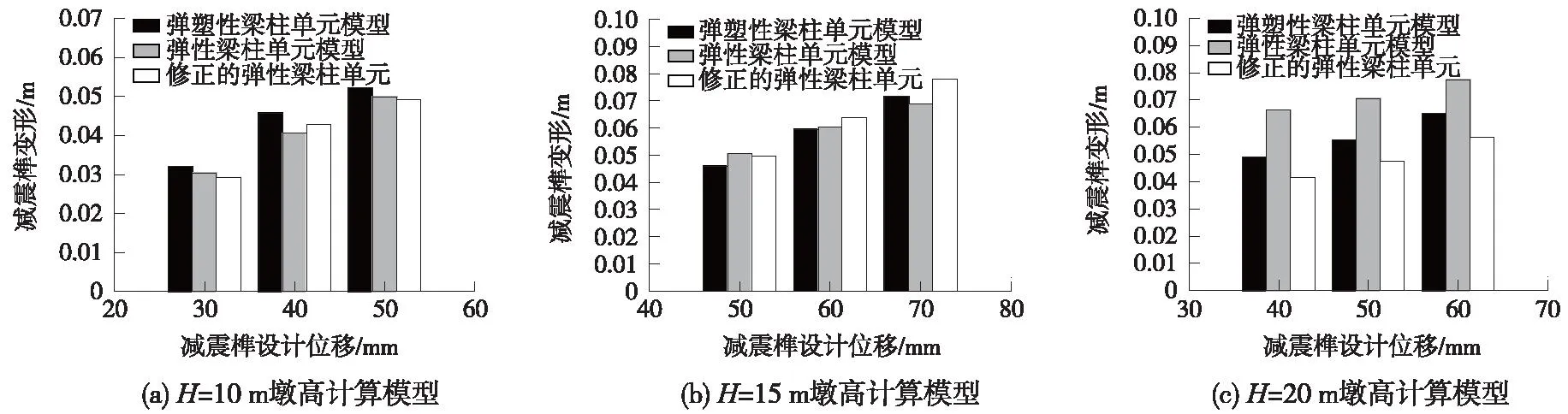
图9　3种计算模型的减震榫变形的地震响应比较

由图9可知，3种计算模型在计算减震榫变形时，10 m墩高和15 m墩高的计算结果差别并不大，说明用考虑桥墩刚度修正和不考虑桥墩刚度修正的弹性计算模型都能够对10 m墩高和15 m墩高简支梁减隔震设计方案中减震榫的个数以及设计位移等力学参数予以确定，而在分析20 m墩高简支梁的减震榫变形时，相比弹塑性纤维单元模型，未修正桥墩刚度的弹性梁柱单元模型的计算结果偏大，在减震榫设计位移取40 mm时，误差达到了34%，而考虑了桥墩刚度的修正后，计算误差缩小至15%以内。

3.5桥墩位移延性与弹性梁柱单元计算模型计算误差的关系

通过以上分析可知，由于在罕遇地震作用下，即使安装了减震榫，随着墩高的增加墩身质量贡献不断增大，桥墩的位移延性比(墩顶位移响应与屈服位移之比)也会超过0.5。在这种情况下，采用考虑桥墩刚度修正的弹性计算模型可以较为准确地估计墩底剪力、墩底弯矩、墩顶位移和减震榫变形等各项地震响应，这种建模方法可以应用在罕遇地震作用下的减隔震设计中(桥墩位移延性比超过0.5的情况)。为了较为直观地观察采用桥墩刚度修正和不采用桥墩刚度修正的计算模型在估计罕遇地震作用下各项地震响应的误差随桥墩位移延性的变化规律，将各项地震响应的计算误差列于图10中，以弹塑性纤维梁柱单元模型的计算结果为基准。

由图10可知，在桥墩位移延性超过0.5的情况下，修正桥墩刚度的弹性计算模型极大地降低了采用桥墩毛截面刚度的弹性计算模型的误差。尤其是在估计桥墩墩顶位移时，误差随着桥墩位移延性的增加呈现明显的降低，误差从65%作用降低至30%以内。而在估计墩底剪力、墩底弯矩、减震榫变形时，在桥墩位移延性超过0.7时，采用桥墩毛截面刚度的弹性计算模型会产生较大的误差，这使得该模型不再适用于桥梁的减隔震设计。通过以上分析可知，随着桥墩高度的增加，墩身质量贡献程度的增加，即使安装了减震榫，桥墩的位移延性也会超过0.5，例如20 m高桥墩的简支梁桥，此时若采用弹性计算模型进行减隔震设计，就需要对桥墩的刚度进行修正。

4结论

针对Ⅱ类场地的高速铁路减隔震桥梁，建立了不同墩高的空间有限元计算模型，在模拟桥墩时考虑了3种方案，即弹塑性纤维梁柱单元、弹性梁柱单元以及考虑刚度修正的弹性梁柱单元。选择了与设计反应谱相匹配的7条强震记录并予以调整，作为地震输入进行非线性时程分析，针对墩底剪力、墩底弯矩、墩顶位移以及减震榫变形这4项地震响应参数，以弹塑性纤维梁柱单元模型的计算结果为基准，探讨适用于罕遇地震作用下的高速铁路减隔震桥梁的合理计算模型。通过分析得到以下结论。

图10　弹性桥墩模型的桥墩位移延性与分析误差的关系

(1)在计算低墩减隔震简支梁桥在罕遇地震作用下的墩底剪力、墩底弯矩、减震榫变形时，采用弹性梁柱单元计算模型(桥墩刚度取毛截面刚度)能够得到较为准确的计算结果，而墩底位移地震响应的计算结果会偏小。

(2)随着墩高增加，桥墩自身质量对地震响应的贡献逐步增大，此时采用弹性梁柱单元计算模型(桥墩刚度取毛截面刚度)计算出的罕遇地震作用下的墩底剪力、墩底弯矩都偏大，而墩顶位移会偏小，偏差随着墩顶位移延性的增加而增大。

(3)采用考虑桥墩刚度修正的弹性梁柱单元计算模型能够较好的模拟罕遇地震作用下的计算结果，尤其是当桥墩位移延性超过0.5时，在分析墩底剪力、墩底弯矩、减震榫变形、墩顶位移的地震响应时都能够得到较为准确的计算结果，该计算模型适用于桥墩较高或位移延性较大的情况。

参考文献：

[1]郑健.中国高速铁路桥梁建设关键技术[J].中国工程科学，2008，10(7)：18-27.

[2]倪燕平.低屈服点钢阻尼器在高速铁路简支梁桥中的应用研究[J].铁道建筑，2013(6)：14-17.

[3]孟兮，高日，李承根.铁路简支梁桥中减震榫的设计及其减震性能研究[J].桥梁建设，2014，44(3):81-86.

[4]徐升桥.铁路桥梁罕遇地震设计研究[J].铁道工程学报，2008(S)：158-164.

[5]卢皓.罕遇地震作用下高速铁路简支梁桥抗震性能分析[J].铁道标准设计，2015，59(8):102-106.[6]钟铁毅，杨凤利，吴彬.铅芯橡胶支座隔震铁路简支梁桥双向地震响应分析[J].中国铁道科学，2008，28(3):38-43.

[7]聂晋涛.客运专线桥梁中减隔震技术应用研究[J].铁道工程学报，2012，28(3):53-57.

[8]Taucer F F, Enrico S. Fiber beam-column model for seismic response analysis of reinforced concrete structures[R]. EERC 91-17，1991.

[9]Mander J B，Priestley M J N, Park R. Theoretical Stress-Strain Model for Confined Concrete. J. Structural Eng.，ASCE，1988，114(8):1804-1826.

[10]Menegotto M，Pinto P E. Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending[C]. Proceedings，IABSE Symposium on Resistance and Ultimate Deformability of Structures，Lisbon，1973:15-22.

[11]周云.耗能减震加固技术与设计方法[M].北京：科学出版社，2006.

[12]Wen Y K. Equivalent Linearization for hysteretic systems under random excitation [J]. Journal of Applied Mechanics，1980，47(1):150-154.

[13]中华人民共和国住房和城乡建设部.CJJ166—2011城市桥梁抗震设计规范[S].北京:中国建筑工业出版社，2011.

[14]中华人民共和国住房和城乡建设部.GB 50111—2009铁路工程抗震设计规范[S].北京：中国计划出版社，2009.

[15]吕红山，赵凤新.适用于中国场地分类的地震动反应谱放大系数[J].地震学报，2007，29(1)：67-76.

[16]Ambraseys N N，Douglas J，Rinaldis D，et al. Dissemination of European strong-motion data[M]. vol. 2，CD-ROM collection. Engineering and Physical Sciences Research Council，UK，2004.

[17]Bommer JJ. Acevedo AB，Douglas J. The selection and scaling of real earthquake accelerograms for use in seismic design and assessment [C]. Proceedings of ACI International Conference on Seismic Bridge Design and Retdt，American Concrete Institute, 2003.

收稿日期：2015-11-03； 修回日期：2015-11-18

基金项目：国家重点基础研究发展计划(2013CB036302);中国博士后科学基金资助(2014M562526XB)

作者简介：卢皓(1984—)，男，工程师，工学博士，主要从事桥梁抗震方面的研究，E-mail：963alex@tongji.edu.cn。

文章编号：1004-2954(2016)06-0048-07

中图分类号：U238； U442.5+5

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.06.011

Investigation on Rational Analytical Model for High-speed Railway Simply-supported Girder Bridge with Steel Dampers under Strong Earthquake Motion

LU Hao

(1.China Railway First Survey and Design Institute Group Co.，Ltd.，Xi’an 710043，China; 2.Department of Bridge Engineering，Tongji University，Shanghai 200092，China)

Abstract：Elasticity beam-column element with gross section stiffness is generally used to simulate seismic response of isolated bridge piers in force-based seismic design method，because pier and foundation are considered to keep elastic state for the sake of safety. Actually，cracking of cover concrete in the bottom section of the pier appears before yield state under rare occurrence earthquake，and may lead to stiffness reduction. Therefore it is appropriate to estimate earthquake response parameters using elasticity beam-column element with stiffness correction of pier，which is helpful for the displacement-based seismic design. For simply-supported girder of high-speed railway in West China，three numerical analysis models are constructed to give rise to the rational model of high-speed railway simply-supported girder bridges with steel dampers under strong earthquake motion. The numerical model is a numerical analysis model respectively with elastic-plastic fiber beam-column element，elasticity beam-column element，as well as elasticity beam-column element in consideration of stiffness correction of pier. The results show that the numerical analysis model with elasticity beam-column element considering stiffness correction of pier is suitable for calculating earthquake response parameters of bridge in case the displacement ductility of pier is more than 0.5．

Key words：High-speed railway; Simply-supported girder bridge; Seismic mitigation and isolation; Analytical model; Elastic-plastic fiber beam-column element; Nonlinear time history analysis