基于扩张状态观测器的列车轨迹跟踪控制及其在CMC环境的测试
2016-08-01侯晓伟
郭 亮,侯晓伟,蔡 虎
(1.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044;2.北京交通大学电子信息工程学院,北京 100044)
基于扩张状态观测器的列车轨迹跟踪控制及其在CMC环境的测试
郭亮1,侯晓伟1,蔡虎2
(1.北京交通大学轨道交通控制与安全国家重点实验室,北京100044;2.北京交通大学电子信息工程学院,北京100044)
摘要:在列车运行过程中,存在着复杂且不确定的外部环境,很难获得阻力的表达式和阻力系数,因此,准确的外部阻力估计直接影响到列车轨迹跟踪精度。设计一种新型的基于扩张状态观测器的列车轨迹跟踪控制算法,将外部阻力和内部干扰扩展为一个新的状态变量,并进行精确估计。采用遗传算法对扩张状态观测器的参数进行优化。最后,在国产CMC芯片的硬件环境下进行测试。测试结果表明,基于扩张状态观测器的控制策略比现有广泛使用的PID算法具有更好的跟踪性能。得出以下结论:所设计控制算法通过补偿各种干扰的影响达到列车位置和速度的精确追踪,具有较强的抗干扰性。
关键词:列车自动控制;列车轨迹跟踪;扩张状态观测器;CMC芯片
铁路作为国家重要基础设施和大众化交通工具,承担着旅客周转和货物流通的重大责任。经过近十年的高速铁路建设和对既有铁路的高速化改造,中国目前已经拥有全世界最大规模以及最高运营速度的高速铁路网。截止2014年底,中国高铁总里程达到1.6万km,“四纵”干线基本成型[1]。铁路的快速发展则带来了许多与之相关的技术问题,铁路系统能否安全高效的运行成为其技术核心,因此采用更为安全、先进的列车自动控制策略进行保证其运营质量十分有必要[2]。
列车追踪问题主要包括追踪列车间隔时间、列车轨迹曲线追踪等,影响着列车运行安全性和区间通过能力。由于高速铁路列车追踪间隔时间计算法完全不同于普速铁路[3],周艳红等[4]基于列车追踪通用模型对固定闭塞、准移动闭塞及移动闭塞下的运行过程进行仿真,以验算区间安全间隔时间。任国彬等[5]利用着色Petri网建立移动闭塞条件下的高速列车两车追踪控制模型,可有效描述MAS下高速列车追踪过程。凌熙等[6]针对高速铁路追踪列车间隔时间测试没有标准化方法的现状,从司机操纵和站场条件等因素规范测试方法。
由于列车运行环境的复杂性,因此,在列车追踪建模时很难对其建立精确的数学表达式。国内外学者针对此问题,提出了重新建立列车动力学模型与采用智能算法排除干扰的解决思路,并做了大量深入的研究工作[7-9]。自抗扰控制方法由中国科学院韩京清研究员提出,通过设计具有不变性的最速反馈控制,实现了高效的非线性反馈,并利用非线性机制开发了跟踪微分器[10],扩张状态观测器[11],非线性反馈单元等[12],并逐步形成自抗扰控制器。本文采用自抗扰控制中扩张状态观测器,将列车运行过程中的阻力视为“统一干扰”,以达到列车目标距离曲线的精确跟踪。
CMC(Control Model on Chips)控制芯片是第一款面向自动控制的国产芯片,将组态处理、程序存储、信号输入输出、控制算法、通讯接口等全部集成在一个芯片中,实现片内逻辑控制和运动控制,程序处理及调度管理,数字量信号处理,以及多种数据接口通信的功能。
1列车单质点建模
目前,在列车运行牵引计算中,列车动力学模型主要可分为:列车单质点模型和列车多质点模型。其中,列车多质点模型将每节车厢当作单独对象分析,多应用于车厢间作用力分析和列车侧向受力分析。列车单质点模型不仅能够较完整地描述列车的受力特性,而且简化建模过程,降低了运算复杂度,主要应用于列车目标速度-距离曲线控制等过程。
列车运行过程中受力可大致分为牵引/制动力和运行阻力。根据牛顿运动学第二定律,基于时间的列车单质点模型建立如下
(1)
式中,m为列车质量;s(t)和v(t)分别为列车的实时位置和速度;u是列车的牵引/制动力;F0为列车基本阻力;Fi和Fr分别为坡道附加阻力和曲线附加阻力。
列车基本阻力包括轮轴间的摩擦,冲击和振动所损失的动能及空气阻力。基本阻力的计算十分复杂,难以用纯理论公式推算,只能通过大量试验得到经验公式。这些公式都是用单位阻力的形式表示的。所谓单位阻力指的是基本阻力作用在列车每kN重力上的值。其表达式为
(2)
式中,a为滚动阻力系数;b为滑动摩擦和滚动摩擦等系数;c为列车阻力系数。该表达式称为“戴维斯方程”,其广泛应用在列车动力学领域。
Fi为坡道附加阻力,是由列车重力的水平分力组成。其表达式为
(3)
式中,α为坡度的倾斜角度。当α足够小时,sinα≈tanα。因此,坡道附加阻力可重写为
(4)
式中,i为坡度值,单位为‰,随着坡度的上下,i可相应取值正负。
Fr为曲线附加阻力。机车车辆在曲线上运行时,受到的运行阻力大于在直线上的运行阻力,其增大部分叫曲线附加阻力。其表达式为
(5)
式中,r为列车运行线路的半径。
2基于扩张状态观测器的列车轨迹跟踪控制方法
2.1基于扩张状态观测器的列车轨迹跟踪设计
列车轨迹跟踪目的为实现对目标速度-距离曲线的跟踪。假设列车的位移跟踪误差 和速度跟踪误差为
(6)

(7)
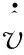
此时该系统满足状态观测器应用条件[13]。
设计三阶扩张状态观测器为
(8)
式中,防振颤函数fal(e,α,δ)为
(9)
通过选择合适的参数,则可满足关系
可见,通过非线性扩张观测器式(8),能够实现对被控对象的位移、速度和“总外部干扰”的精确估计。由于抽样间隔h足够小,t时刻和t+h时刻的“总外部干扰”e3(t)可以看作近似相等,实现对未知不确定性和外加干扰的补偿。因此设计控制器为
(10)
式中,α,β,λ和μ为常数且满足α>0,β>0。
2.2控制器稳定性和误差分析
将式(10)代入式(7),则可得新的误差方程
(11)
定理1:对[a,∞),a∈R上可微的函数f(t),若其极限存在,并且f(t)的导数有界,则该函数在其定义域内一致连续。

引理2:(类李雅普诺夫引理)在一个开球域内,如果存在一个标量函数V(x,t)满足下列条件:
· V(x,t)有界;



定理2:若含有外部阻力的列车单质点动力学模型如式(1)所示,和连续时间误差方程如式(6)所示,基于扩张状态观测器设计的控制器如式(10)所示,则该控制器能够保证当t→∞时,列车的位移跟踪误差e1(t)和速度跟踪误差e2(t)分别趋向于零,即
且闭环系统渐近稳定。
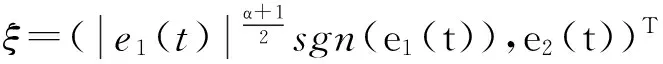

取

代入上式,则可得
(12)
则系统渐近稳定。


观察状态变量e1(t),e2(t)的运动方程为
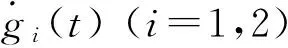
由e2(t)趋于零知g2(t)趋近于零。根据上述结论,则可知g1(t)同样趋于零。即有
定理1得证。
2.3基于遗传算法优化的观测器参数整定
尽管基于扩张状态观测器的控制器具有较强的鲁棒性和优越的适用性,但观测器中参数选择成为制约控制器性能的重要因素。上文中所包含的β1,β2,β33个参数需要进行合理的整定以达到列车轨迹的精确跟踪。黄一在设计观测器时[11],对其做出了基本试凑,但是该方法耗时长,精度低。在现代优化算法中,遗传算法在计算时只需要影响优化的目标函数和相应的适应度函数,对复杂问题提供了通用框架,适合于大规模复杂问题的优化。因此,该部分对观测器中的参数基于遗传算法进行整定。
(1)遗传算法优化流程
由于优化目标参数较少,二进制编码能够反映所求问题的结构特征和信息,加之其编码、解码简单易行,因此采用基于二进制编码方案的遗传算法对参数进行整定。下面5个步骤为对目标参数进行优化。
①确定参数的约束条件和编码

②确定解码方式
解码时需将30位长的二进制编码串切割为3个10位长的二进制编码串,然后分别将它们转换为对应的十进制整数代码,分别记为y1,y2和y3。依据个体编码方法和对定义域的离散化方法可知,可将yi转换为变量βi的编码公式为
③确定个体评价函数
遗传算法的应用目的在于使变量误差e(t)最小化。因此,设计统一的个体评价方法可以筛选最优解。目前,应用广泛的判断标准的性能指标有积分平方误差准则(Integral of Squared Error,简称ISE),积分误差绝对值准则(Integral of Absolute value of Error,简称IAE)和积分时间和误差的平方值准则(Integral of Time and the Squared value of Error,简称ITSE)。而积分时间和误差的绝对值的乘积准则(Integral of Time Multiplied by the Absolute Value of Error,简称ITAE)能够为系统提供一个全面的性能指标。因此,取ITAE为作为适应度函数
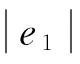
④惩罚策略
在列车运行过程中,列车的牵引/制动力往往存在饱和特性。而如果单纯考虑评价函数,可能会产生最优解所对应的牵引/制动力超出实际限定范围。因此必须引入惩罚因子来调节控制器的大小。同时,由于实际驾驶过程中牵引动作和制动动作的切换开关频率不应过大,因此加速度的变化率也应视为一项惩罚的指标。对于超越边界的染色体编码直接给出较大的惩罚值,从而在筛选时剔除。考虑这些因素,适应度函数改进为
式中,Umax和Umin为牵引/制动力的上下界;A为加速度变化率的最大值;M为一个足够大的惩罚值。
⑤选择,交叉和变异运算
首先,采用适应度比例法生成新的染色体,其次,单点交叉的概率为Pc,最后,基本位变异策略的变异概率为Pm。
(2)遗传算法优化参数仿真
在本文的仿真研究中,遗传优化算法的参数选择如下:
终止进化代数G=50;
群体大小M=30;
交叉概率Pc=0.6;
变异概率Pm=0.01。
优化的适应度曲线如图1所示。经过50代的遗传变异,评价值下降至稳定值。此时,经过遗传算法优化后的参数可使控制器达到良好的效果,得到的优化后的扩张状态观测器参数为:β1=172,β2=586,β3=2 520。

图1 适应度(ITAE)曲线
3CMC半实物环境下仿真与分析
3.1基于遗传算法优化的观测器参数整定
为测试该算法搭建了基于CMC芯片的半实物仿真平台,如图 2所示。该平台包括系统硬件和软件两部分内容。系统硬件部分包括外围电路和驱动程序;系统软件部分则是上位机PC端仿真软件[14,15]。其中硬件系统的作用是为列车目标距离曲线控制算法提供硬件运行环境,并且和上位机软件系统进行实时通信以及实现数据的交互;软件系统的作用是实现列车模型的仿真和列车运行环境的仿真,并且和下位机硬件系统进行数据通信,其系统结构框图见图3。

图2 基于CMC芯片的半实物仿真平台
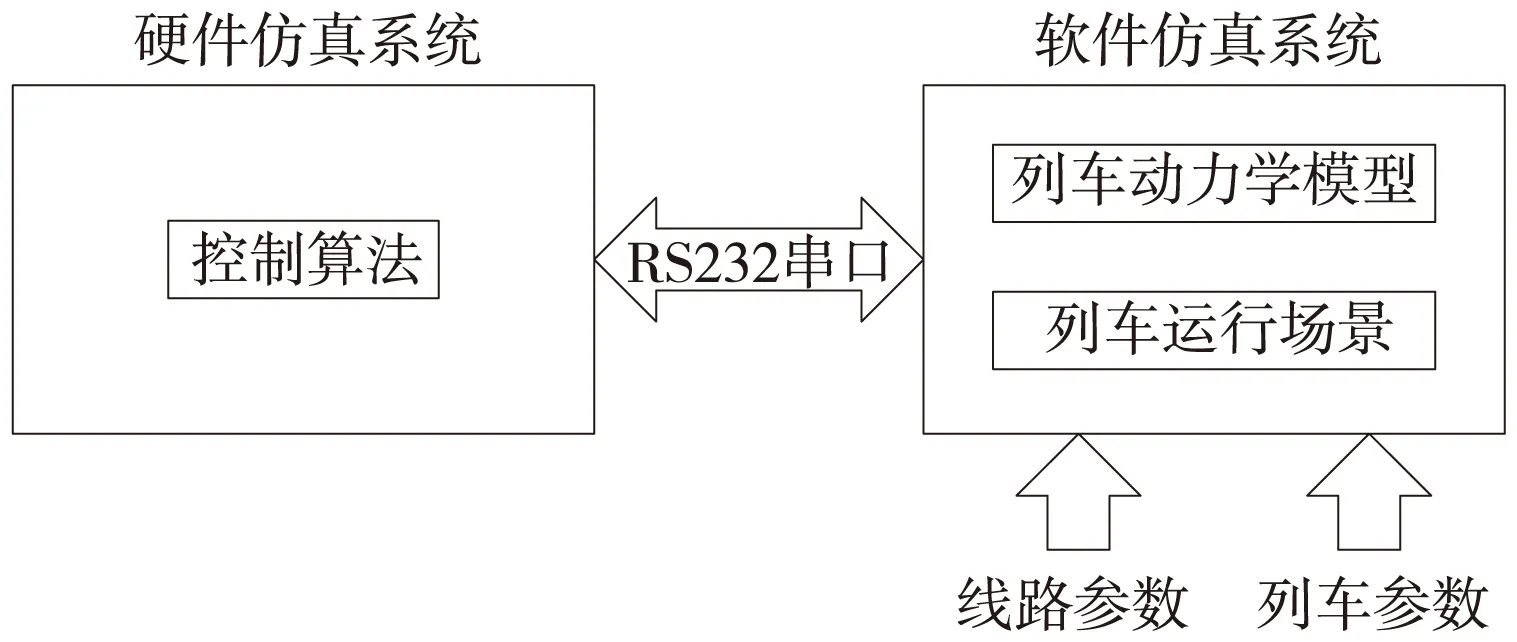
图3 系统结构框图
3.2基本线路条件下仿真
本节通过在试验线路条件下设计不同场景中的仿真算例,验证基于扩张状态观测器的列车轨迹跟踪控制算法的精确性和抗干扰性。其中,试验线路以某线路一段为基础,并参考和计算其坡度,曲线半径等数据,达到逼近实际应用环境的目的。
本算例中采用和谐号CRpA型动车组,其编组总质量为3.45×105kg。若按其标准载客量610人,每名旅客质量估算为60 kg,则列车总质量为3.816×105kg。重力加速度取9.8 m/s2。该试验线路总长为3 500 m,列车运行时间为200 s。其他线路参数如表 1所示。
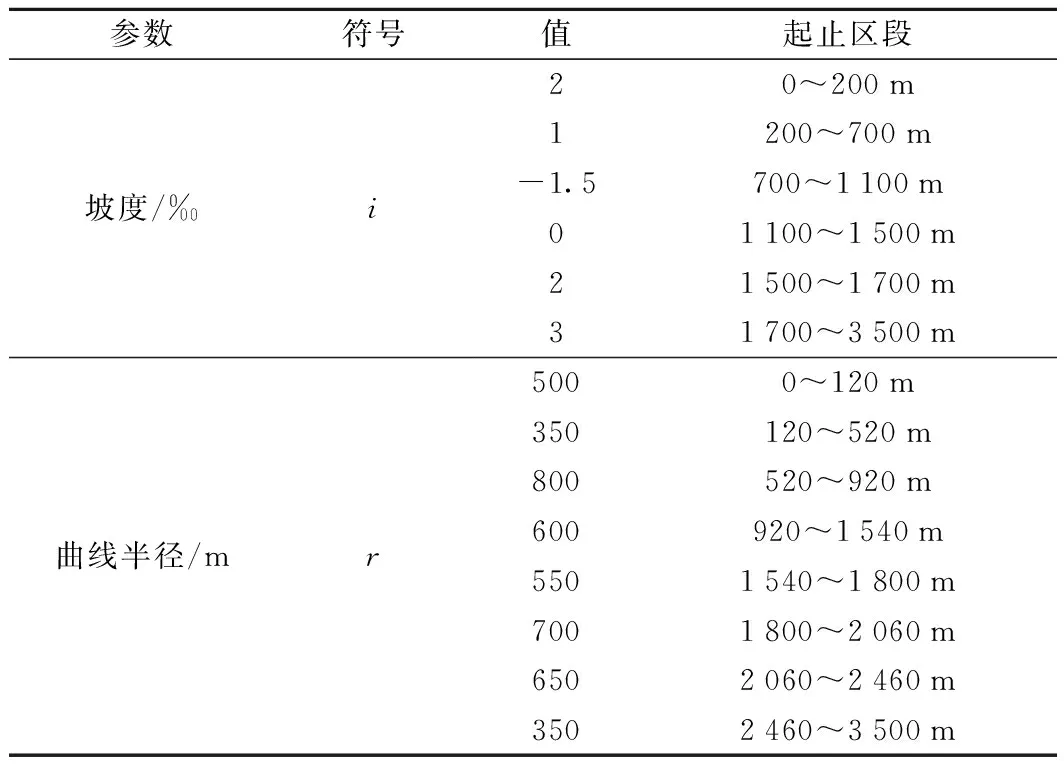
表1 线路基本信息
列车运行的目标位置曲线和目标速度曲线如图4所示,其中试验线路中多处存在临时限速。基本线路条件下基本阻力表示为
F0=2.4+0.014v+0.001 293v2
图中,蓝线表示基于扩张状态观测器的列车运行控制算法的速度追踪与位置追踪曲线。仿真结果表明达到了良好的追踪目的。

图4 基于扩张状态观测器的控制算法在CMC平台测试的跟踪效果
在目前的列车运行控制系统中,通常采用PID算法追踪目标速度-距离曲线,有些系统为了减少计算量,提高实时性,只采用了PI算法,甚至单纯的比例算法。为了进一步验证所设计控制的良好追踪效果,在同等线路条件下采用基于遗传算法优化的PID控制策略进行对比参照。PID经优化得到的参数为Kp=12 115,Ki=963,Kd=5.814。仿真结果如图5、图6所示。结果表明,PID控制算法和基于扩张状态观测器的列车轨迹跟踪控制算法都达到了规定误差限度内的精确跟踪,但在线路坡道转换处,曲线半径切换处,后者表现出了更强的抗干扰能力,而PID算法则出现了一定的波动,影响了跟踪效果。

图5 基本线路条件下ESO控制追踪误差
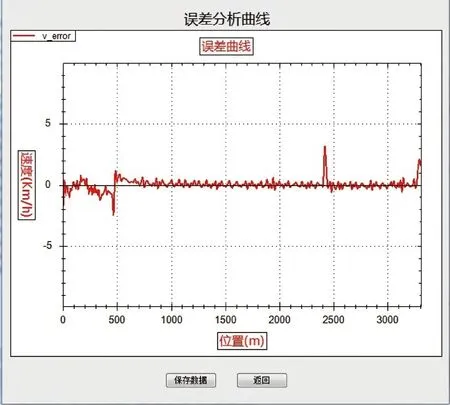
图6 基本线路条件下PID控制追踪误差
4结语
本文设计了基于扩张状态观测器的列车轨迹跟踪控制算法,并采用遗传算法进行了参数优化,达到了提高列车轨迹跟踪能力和精度的目的。通过使用经典的单质点列车动力学模型,扩张状态观测器精确地估计了外部阻力和未知部分。同时,该方法也被应用于减少未知阻力和干扰造成的影响。仿真结果表明,基于扩张状态观测器的控制策略比现有广泛使用的PID算法具有更好的跟踪性能。
参考文献:
[1]樊曦.中国高铁运营里程达到1.6万公里 位居世界第一[N/OL].(2015-01-29)[2015-10-11]http://news.xinhuanet.com/2015-01/29/c_1114184446.htm.
[2]H.R. Dong, B. Ning, B.G. Cai, Z.S. Hou. Automatic Train Control System Development and Simulation for High-Speed Railways[J]. IEEE Circuits and Systems Magazine, 2010(2):6-18.
[3]田长海,张守帅,张岳松,等.高速铁路列车追踪间隔时间研究[J].铁道学报,2015(10):23-27.
[4]周艳红,唐金金.高速列车追踪运行过程仿真方法研究[J].铁道标准设计,2012(8):116-120.
[5]任国彬,陈小强.基于着色Petri网的高速列车追踪运行过程建模与仿真[J].铁道标准设计,2015(3):122-126.
[6]凌熙,杨文韬.高速铁路追踪列车间隔时间测试方法标准化研究[J].铁道标准设计,2015(10):23-26.
[7]G. Bing, H.R. Dong, B. Ning. Speed Control Algorithm for Automatic Train Operation Systems[C]∥IEEE Int. Conf. Computational Intelligence and Software Engineering, 2009:1-4.
[8]H.R. Dong, S.G. Gao, B. Ning, et al. Extended fuzzy logic controller for high speed train[J]. Neural Computing and Applications, 2013(2):321-328.
[9]X.B. Sun, H. Cai, X.W. Hou, et al. Energy consumption analysis with trip time for a single train[C]∥26th Chinese Process Control Conference, 2015: 1-5.
[10]韩京清,王伟.非线性跟踪微分器[J].系统科学与数学,1994(2):177-183.
[11]黄一, 韩京清.非线性二阶连续扩张状态观测器的分析与设计[J].科学通报,2000(13):1373-1379.
[12]韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.
[13]J.Q. Han. From PID to active disturbance rejection control[J],. IEEE trans. on Industrial Electronics, 2009(3):900-906.
[14]侯晓伟,孙绪彬,蔡虎,等.基于ARM的列车运行控制算法仿真测试系统[C]∥第26届中国过程控制会议,2015:20-25.
[15]X.B. Sun, H. Cai, X.W. Hou, et al. Regenerative braking energy utilization by multi train cooperation[C]∥Intelligent Transportation Systems (ITSC), 2014 IEEE 17th International Conference on IEEE, 2014:139-144.
收稿日期:2015-11-19; 修回日期:2015-12-02
基金项目:国家863计划项目(2012AA041701-3)。
作者简介:郭亮(1990—),男,硕士研究生,主要从事列车控制算法研 究,E-mail:13120238@bjtu.edu.cn。
文章编号:1004-2954(2016)07-0144-06
中图分类号:U284
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2016.07.033
Train Trajectory Tracking Control Based on Extended State Observer and Its Simulation Test in CMC Environment
GUO Liang1, HOU Xiao-wei1, CAI Hu2
(1.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China;2.School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract:In the process of train operation, it is difficult to obtain the expression and the coefficient of the resistance due to the complex and uncertain external environment. Therefore, the accurate estimation of the external resistance is the key factor to the accuracy of the tracking. Thus, a novel train trajectory tracking control algorithm based on the extended state observer is designed, which extends all kinds of resistances to a new state variable for precise estimation. The genetic algorithm is applied to optimize the parameters of the extended state observer. Finally, test is conducted in home-made hardware environment of CMC chip. The test results show that the control strategy based on the extended state observer has better tracking performance than that of the existing PID algorithm. It is concluded that the proposed control algorithm can achieve accurate position tracking and velocity tracking with strong anti-interference ability.
Key words:Automatic train operation; Train trajectory tracking; Extended state observer; CMC chip
