采空区顶板动力响应数值模拟研究

梁 超

(昆明理工大学 国土资源工程学院，云南 昆明 650093)



采空区顶板动力响应数值模拟研究

梁 超

(昆明理工大学 国土资源工程学院，云南 昆明 650093)

介于岩体材料及爆破地震波的复杂性，采用理论分析方法难以对采空区顶板动力响应做出准确计算，而且求解出的计算公式通常比较复杂，工程上难以直接应用。FLAC3D数值模拟软件中的动力分析功能在解决岩土工程方面的非线性动力分析问题方面有巨大优势，能更深入的研究采空区顶板在爆破震动作用下的动应力场、动位移场和塑性区的变化规律及动静应力场的叠加作用机理。在理论研究的基础上，借助FLAC3D提供的动力分析功能，建立数值计算模型，对静力荷载和爆破动载共同作用下采空区顶板失稳过程和机理进行数值模拟分析。

爆破地震波；动力响应；采空区顶板；数值模拟

0 前 言

爆破作业是金属类矿山在开采过程中非常重要且必不可少的工序，不论是生产还是掘进都需要进行大量爆破作业，而爆破必然产生震动，对周围岩体形成动力加载环境，如果动荷载强度达到某一程度会直接造成围岩的动力失稳破坏。另一方面，采空区顶板在爆破地震波的反复动力加载作用下，其宏观力学性能将逐渐被弱化乃至最终失效或形成连续非线性的累积损伤。所以，爆破震动效应对采空区围岩造成的危害不能被忽略[1-3]。

介于岩体材料及爆破地震波的复杂性，采用理论分析方法难以对采空区顶板动力响应做出准确计算，而且求解出的计算公式通常比较复杂，工程上难以直接应用。而随着计算机软件技术的广泛应用，为研究岩体结构动力响应提供了一种新方法。鉴于数值模拟的特点和求解非线性动力问题的优越性，用数值计算的方法来研究爆破地震作用下采空区顶板结构动力响应的规律已成为爆破领域研究方法的一个必然趋势[57]。FLAC3D数值模拟软件中的动力分析功能在解决岩土工程方面的非线性动力分析问题具有巨大的优势。为更深入的研究采空区顶板在爆破震动作用下的动应力场、动位移场和塑性区的变化规律及动静应力场的叠加作用机理，本章在前面理论研究的基础上，借助FLAC3D提供的动力分析功能，建立数值计算模型，对静力荷载和爆破动载共同作用下采空区顶板失稳过程和机理进行数值模拟分析。

1 数值模拟软件概述

FLAC是连续介质快速拉格朗日差分分析方法的英文缩写，是专门为岩土工程稳定性分析设计和服务的程序，属于有限差分软件。他能够准确模拟材料的塑性破坏和流动，能够对土质岩石材料进行力学特性模拟和塑性流动分析，具有与岩土工程实际拟合好，计算稳定性好、收敛快的特点，因此目前是包括水电、矿业、公路、铁路等岩土工程领域求解三维问题时普遍采用的理想分析工具[4]。

FLAC3D的基本计算原理是将计算区域划分为若干四面体单元，用节点将各个单元相互连接，当某个节点受到荷载作用后，其运动方程可以用时间步长的有限差分形式表示，并且荷载只对该节点周围的若干节点有影响。程序根据单元节点的速度变化来计算单元之间的相对位移，进而可以求出单元应变，然后根据单元材料的本构关系即可求出单元应力。

FLAC3D中为岩土体工程问题的求解提供了11种力学模型和5种计算模式，其中岩土工程常用的力学模型有Null model开挖模型、Mohr-Coulomb塑性模型和Drucker-Prager塑性模型；而常用的计算模式有静力模式、动力模式、渗流模式及蠕变模式。其中，静力模式是是FLAC3D默认的计算模式。动态分析时，要先进行静力计算，并在此基础上打开动力计算功能，设置动态边界然后直接施加速度或应力荷载进行动力扰动分析。

2 数值模型的建立及计算方案

2.1计算模型区域及几何尺寸

本文根据某矿竖向排列采空区建立数值计算模型。根据矿体开挖尺寸和上部围岩特点，设置模型尺寸的长度为290 m，宽度为220 m，高度为200 m。模型由上下两个横截面为矩形的采空区组成，并且不考虑上方采空区跨度的变化，两个采空区的长宽高尺寸均为42 m×36 m×18 m。以竖直方向为模型的Z轴，沿矿体走向方向为Y轴，水平方向内垂直矿体走向设为X轴。模型的Z轴的正方向范围即0 m≤Z≤200 m为数值计算区域，X方向的计算范围是 ，Y方向的范围为0 m≤Z≤290 m。网格单元的划分采用不等划分，根据需要对模型开挖部分的网格划分的细一些，对模型的外部较远的区域划分相对稀疏。模型内共划分了79 296个单元，85 140个节点，三维计算模型及网格划分如图1所示。

图1 计算模型及网格分布

本次模拟分析中，静力计算和动力计算均采用Mohr-Coulomb强度准则，其屈服函数为：

(1)

ft=σ3-σt

(2)

式中：Nφ=(1+sinφ)/(1-sinφ)，其中φ为内摩擦角；σ1，σ3分别为最大和最小主应力；c为黏聚力；σt为岩石抗拉强度。当岩体内某一点应力满足fs<0时发生剪切破坏；当岩体内某一点应力满足ft>0时发生剪切破坏。计算所需的岩体力学参数见表1。

表1 岩体力学参数取值

2.2初始条件与边界设置

2.2.1 初始地应力场

原岩应力是岩土工程数值模拟计算中的一个基本参数。其数值的大小，尤其是水平应力与垂直应力的比值，对计算结果的影响往往大于计算模型等因素的影响。因此，确定原岩应力是计算分析中的一个基本问题。一般来说，原岩应力大小和方向的确定，有效的方法是进行现场实测。由于没有进行现场地应力测试，初始地应力场仅按自重应力场考虑。根据弹性原理，竖向应力σv=γH，水平应力σh=kσv。其中：γ为岩体容重，H为埋深；k为侧压力系数，k=v/(1-v)；v为泊松比。

2.2.2 静力计算边界条件

静力分析过程中采用位移边界条件，由于采动的影响范围有限，离采场较远处岩体位移值很小，将模型边界处位移视为零，即在计算模型的左右(X方向)边界、前后(Y方向)边界和底边界(Z=0)均施加位移约束条件，上边界为自由边界。模型顶部距离地面的平均距离为200 m，将模型上方岩体的作用转化成面力垂直向下施加在模型的上部(Z=200)。

2.2.3 动力计算边界条件

在进行动力分析时，合理设置模型周围的边界条件是非常重要的，因为在边界上会产生波的反射影响，在一定程度上会对动力分析模拟的结果产生较大影响。如果把计算模型设置的很大，虽然可以消除反射波的影响，分析结果也会得到很大的改善，但是较大的计算模型会导致单元数与节点数增多，从而使计算时间大大增加。FLAC3D提供了静态(黏性)和自由场两种边界条件设置来减小波在模型边界上反射[61]。自由场边界一般应用于地面结构的动力分析，考虑到采空区位于地表以下位置，因此本次计算模型动力分析在底边界和侧向边界(包括X方向和Y方向)设置黏性边界条件来吸收边界上的入射波。上方采空区的底板设置为动荷载边界，其他采空区边界均设为自由边界。

2.3力学阻尼与中心频率的选取

采用FLAC3D求解动力方程的方法可解决准静力问题和动力问题两类力学问题。在这两类问题中都要使用阻尼，但准静力问题需要更多的阻尼使得动力方程能够更快的收敛平衡。对于动力问题中的阻尼，需要在数值模拟中重现自然系统在动荷载作用下的阻尼大小。阻尼的存在使得能量产生了消耗，并且引起质点位移和速度的衰减。在动力分析中，FLAC3D提供了瑞利阻尼、局部阻尼和人工粘滞阻尼3种形式[61]。常用临界阻尼值范围一般在2%～10%。对于岩土材料而言，在进行动力计算时多数能量耗散在塑性流动阶段，因此在进行大应变的动力分析时只需设置一个较小的阻尼比即可。本文采用的是瑞利阻尼。对于比较简单的模型可用自振频率作为瑞利阻尼的中心频率，通过重力作用下无阻尼的自振计算求得。本文计算模型中心频率取为30 Hz，阻尼比取5%时系统振幅方能得到较好的减弱。经测试，地震波在0.3 s后完成基本衰减，故系统模型受动态扰动时间选取0.3 s。

2.4爆破震动载荷的施加

在FLAC3D动力计算中，动载荷输入可以采用加速度时程、速度时程、位移时程和应力时程4种不同方式，若采用粘滞边界条件，则必须输入速度时程进行分析。数值计算中可以将施加的爆破地震荷载简化为谐波的形式或者简化为三角形荷载的形式。根据第四章的理论分析，本章采用谐波形式的应力激励动荷载模型，并将简化后的谐波动荷载施加于上方采空区的底板，沿Z轴负方向传播，进行爆破动荷载作用下采空区顶板动力响应状况计算，包括应力、位移及塑性区的变化与分布情况。

2.5计算方案与监测点

为研究竖上下交叠采空区隔层顶板在开挖形成的静力荷载以及爆破震动荷载作用下的稳定性分析采空区顶板在不同振幅、不同频率的爆破震动荷载作用下的动力响应变化规律设计了以下4种计算方案：a 初始应力条件下对矿体模型上下两个空区同时进行开挖，计算至静力平衡，得到采空区隔板在自重静荷载作用下的应力、位移及塑性区并监测隔层顶板下表面中间部位应力和位移变化；b 在爆破地震波荷载峰值为1 MPa时，频率分别为20，50，100 Hz的不同地震波频率下隔层顶板的动力响应；c 在频率为50 Hz，地震波荷载峰值分别为0.5，1，1.5，2 MPa时的动荷载作用下顶板的动力响应规律；d 隔层顶板在频率为100 Hz，动荷载峰值为0.5 MPa的爆破动荷载作用下的响应。

由固体力学理论可知，在自重和动荷载作用下采空区顶板的最大位移发生在空区间隔板的底部中心位置。所以为研究采空区隔板在爆破荷载作用下的动力响应变化规律，选取隔板中间竖直方向截面上的节点作为位移和应力的跟踪监测点，在隔板厚度为10 m时该点在模型上的坐标为(145,1,73)。

整个计算过程分二步进行。先进行静力分析，然后在此基础上再施加动力荷载进行动力问题的分析。在第1步静力分析前，先关闭动态分析模式，在模型边界施加水平和竖直方向应力，形成初始地应力场，然后将采空区一次性开挖并计算至平衡状态，分析采空区顶板在静荷载作用下的变形，并将其围岩静态应力场结果作为第2步动态扰动的初始应力场。第2步输入动力荷载简化为谐波形式的应力激励施加于模型上部空区底板沿Z轴负方向传播，分析其在爆破荷载作用下的动态响应特征。

3 模拟结果分析与讨论

FLAC在分析输出的应力结果时，他给出的最大主应力，实际上是最小主应力，最小主应力实际上是最大主应力，用这两个应力指标，可表征地压活动在介质应力状态变化方面产生应力集中或应力松驰的程度。且负应力为压应力，正应力为拉应力。根据以上设置建立的模型首先进行原岩应力计算，然后对矿体开挖进行静力计算，开挖后顶板在静荷载作用下的最大主应力云图、最小主应力云图、竖直方向位移云图以及拉伸剪切破坏区域如图2所示。监测点的应力和位移随开挖过程变化的关系见图3。

从图2和图3可以看出：采空区开挖后围岩原始应力平衡被打破，引起应力重分布和局部应力集中，并产生了向采空区方向的位移。在上部采空区的顶板处和下部采空区的底板处均出现较大的拉应力，在空区边界和拐角处出现拉伸剪切破坏区，隔板比较完好中间未出现拉伸破坏区域。当顶板岩体达到再次平衡时，在底部中心处产生的位移和拉应力分别为2 mm、0.85 MPa。

图2 开挖后隔层顶板的位移和应力云图及塑性区

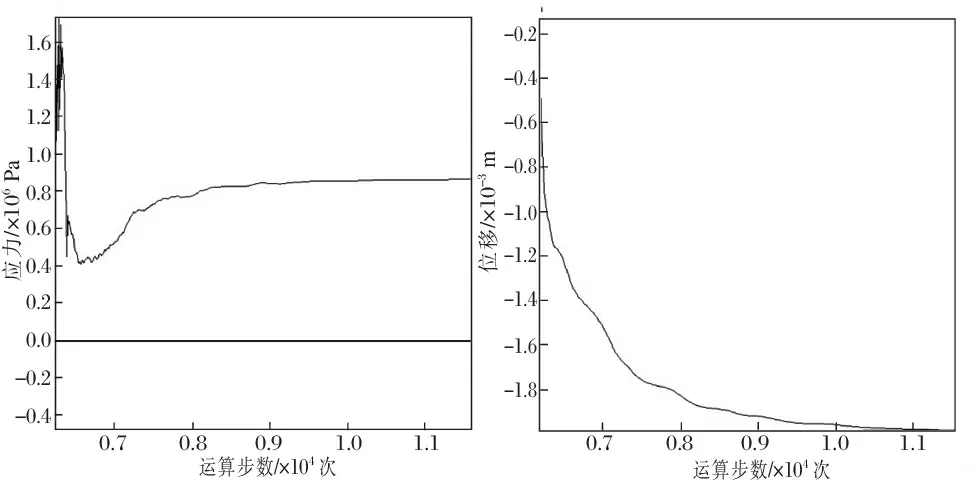
图3 监测点的应力和位移随开挖过程变化曲线

图4分别为在荷载峰值为1 MPa，频率分别为20，50，100 Hz的爆破动荷载作用下隔层顶板的最大主应力和竖向位移局部放大云图。

图4 顶板在不同频率动荷载作用下的最大主应力和位移云图

图5分别为在荷载峰值为1 MPa，频率分别为20，50，100 Hz的爆破动荷载作用下隔层顶板底部监测点的位移和应力随动力计算时间的变化曲线。

图5 顶板在不同频率动荷载作用下的动力响应曲线

从图4和图5可以看出：在爆破荷载峰值相同，频率不同的爆破地震波作用下，隔层顶板的动力响应也不同。顶板的动力响应随着频率的增加先增大后减小，爆破地震荷载频率越大，顶板产生的动拉应力和动位移越小。当频率为50 Hz时顶板的动力反应最大，说明50 Hz频率的爆破地震波对采空区顶板的稳定在影响最大，隔层顶板结构的固有频率与爆破地震波的频率接近，产生共振效应，可能使顶板发生突然失稳破坏。

图6分别为在荷载峰值为0.5 MPa，频率50 Hz的动荷载作用下隔层顶板最大主应力和竖向位移局部放大云图以及隔层顶板底部监测点的位移和应力随动力计算时间的变化曲线。

图6 频率为50 Hz，荷载峰值为0.5 MPa时顶板的动力响应规律

图7分别为在荷载峰值为0.5 MPa，频率100 Hz的动荷载作用下隔层顶板最大主应力和竖向位移局部放大云图以及隔层顶板底部监测点位移和应力随动力计算时间的变化曲线。

图7 频率为100 Hz，荷载峰值为0.5 MPa时顶板动力响应规律

图8是在频率为50 Hz，地震荷载峰值分别为0.5，1，1.5，2 MPa时的隔层顶板塑性区变化。

从图8可以看出：在不同的爆破地震荷载强度作用下顶板的动力破坏程度不同，爆破荷载峰值越大，顶板的动力响应就越大，产生的拉应力也越大。当动荷载峰值为0.5 MPa时，只有隔层顶板上下空区的边界出现塑性区，而当荷载峰值大于1 MPa时隔层顶板受到的拉应力大于其抗拉强度，底部中间区域首先发生拉伸破坏，开始出现小范围塑性区，并随着爆破荷载峰值的增大，顶板发生拉伸破坏的范围也越大，并且破坏区域的形状为拱形。

图8 不同动荷载峰值作用下顶板塑性区变化规律

为了更清楚的观察爆破地震波的频率和振动幅值对顶板动力响应的规律，提取监测点在不同频率不同荷载幅值下的最大拉应力变化值，并将其导入到Matlab中绘制出顶板的动力响应与爆破荷载及频率的关系曲线如图9所示。

图9顶板的动力响应与爆破荷载及频率的关系

从图9可以清晰的看出：采空区隔层顶板在不同频率、不同荷载峰值的地震波作用下的应力变化过程。从以上数值模拟分析可以得出以下结论：爆破地震荷载峰值大小对采空区隔板稳定性的影响最明显，隔板最大位移和最大拉应力随峰值增大而增大，当动荷载峰值超过1 MPa时隔板底部中心部位开始出现拉伸破坏区，并且动荷载峰值越大破坏区域越大；随频率的增大，隔板最大位移和最大应力先增大后减小，当爆破荷载频率接近顶板的固有频率时，顶板产生的动力反应达到最大值，即50 Hz频率的动荷载对采空区隔板的稳定性最不利。

4 结 论

本文以上下交叠地下矿山采空区隔层顶板为研究对象，采用数值模拟方法对采空区顶板在爆破震动作用下的动力响应进行了数值模拟研究。应用FLAC3D计算软件，建立竖向排列的采空区模型。首先模拟出空区开挖以后在静力载荷下顶板的位移和应力变化情况，并在静荷载作用的基础上对模型施加不同峰值的爆破动荷载，对顶板在动静荷载共同作用下的位移场、应力场和塑性区的响应进行了研究，通过对比不同爆破荷载峰值情况下采空区顶板的动力响应来分析对稳定性的影响程度，揭示了动静荷载共同作用下竖向排列采空区隔层顶板失稳破坏机理。

[1] 刘亚群, 李海波. 爆破荷载作用下黄麦岭磷矿岩质边坡动态响应的UDEC模拟研究[J]. 岩石力学与工程学报, 2004, 23(11): 42-45.

[2] 陈占军, 朱传云, 周小恒. 爆破荷载作用下岩石边坡动态响应的FLAC3D模拟研究[J]. 爆破, 2005, 22(4): 8-15.

[3] 逄焕东, 陈士海. 弹性介质中爆破地震波传播的分区变化规律研究[J]. 振动与冲击, 2009(3).

[4] 闫长斌, 徐国元, 李夕兵. 爆破震动对采空区稳定性影响的FLAC3D分析[J]. 岩石力学与工程学报, 2005, 8(16): 2894-2899.

[5] Khandelwal M, Singh T N. Prediction of blast induced ground vibrations and frequency in opencast mine: A neural network approach[J]. Journal of sound and vibration, 2006, 289(4): 711-725.

[6] 傅洪贤, 赵勇, 谢晋水, 等. 隧道爆破近区爆破振动测试研究[J]. 岩石力学与工程学报, 2011, 30(2): 335-340.

[7] 吴姗, 陈何, 孙宏生, 等. 大红山铜矿束状孔采矿及爆破振动监测技术[J]. 有色金属工程, 2015, 5(5): 126-129.

[8] 刘波, 韩彦辉. FLAC原理,实例与应用指南[M]. 北京: 人民交通出版社, 2005.

AStudyonNumericalSimulationofDynamicResponseofRoof

LIANG Chao

(FacultyofLandResourceEngineering,KunmingUniversityofScienceandTechnology,Kunming,Yunnan650093,China)

The roof of mined area is relatively weak, and the goaf roof is one of the most serious accidents in underground metal mines. The underground workers will not only pose a threat to the safety, but also have a significant impact on the production and management of underground pressure. There are many factors to affect the goaf roof stability. The stress distribution and the blasting vibration are the two most important factors. This paper mainly uses the method of theoretical analysis to be combined with numerical simulation, from static and dynamic two aspects of goaf roof stability of the stress in the weight and load of blasting under dynamic loads. The main contents of the thesis are the following: using the elastic vibration theory of thin plate down the top plate under uniform harmonic pulse displacement under load to calculate formulas for stress analysis. The damping, including the dynamic load strength, influence of dynamic frequency response of roof strata, and the dynamic response in the empty mining district under dynamic and static loads of roof are all analyzed.

Blasting earthquake wave; Roof of mined void; Dynamic response; Numerical simulation

2016-07-24

梁超(1991-)，男，宁夏石嘴山市人，在读硕士研究生，研究方向：安全工程，手机：18695200970，E-mail：376677756@qq.com.

TD327.2

：Adoi：10.14101/j.cnki.issn.1002-4336.2016.04.019