输电线路元件的结构可靠度分析

徐 彬，王松涛，曾二贤，吴海洋（中南电力设计院，湖北 武汉 430071）



输电线路元件的结构可靠度分析

徐 彬，王松涛，曾二贤，吴海洋
（中南电力设计院，湖北 武汉 430071）

摘要：为正确评价输电线路的安全性，本文以输电线路元件（导地线、绝缘子和金具）作为分析对象，建立了可靠度分析模型，通过分析影响输电线路元件荷载效应的永久荷载、风荷载的计算公式以及分布曲线，得到荷载效应的统计参数；考虑材料性能不定性、几何参数不定性和计算模式不定性，得到抗力统计参数。采用一次二阶矩方法，计算得到输电线路元件在大风工况下的可靠度指标。结果表明，按现行输电线路规范的安全系数设计的输电线路元件，其可靠度水平较高。研究结果可为输电线路概率极限状态设计方法提供参考

关键词：输电线路；元件；可靠度指标。

输电线路体系是高负荷电能输送的载体，近年来逐渐趋于向大型化复杂化方向发展。导地线、绝缘子和金具作为输电线路系统的一部分，其可靠性直接决定了整个输电系统的安全性及稳定性。对于输电线路的可靠度分析，目前国内外形成了一些有价值的成果。但以往较多的研究注重于杆塔结构分析，而对于输电线路元件导地线、绝缘子和金具的结构可靠度分析，则鲜见于文献。

本文建立了输电线路元件的可靠度分析模型，通过分析影响荷载效应的永久荷载、风荷载的计算公式以及分布曲线，得到荷载效应的统计参数；考虑材料性能不定性、几何参数不定性和计算模式不定性，计算得到抗力统计参数。采用一次二阶矩方法，计算得到输电线路元件在大风工况下的可靠度指标。考虑到目前输电线路的安全性和稳定性愈加重要，为适应我国电力建设事业发展的需要，开展输电线路元件的可靠性研究很有必要且具有实践意义。

1 可靠度分析模型

1.1 现行规定GB 50545—2010中的计算公式

GB 50545—2010《110 kV～750 kV架空输电线路设计规范》规定了输电线路元件各自的设计表达式，可统一按式（1）表达：

式中：K为设计安全系数；Tp为承载力；Tmax为最大拉力。

1.2 极限状态方程

输电线路元件的工作状态可以统一用抗力R与作用效应S表示为：

随着R和S的变化，功能函数Z有三种变化：当Z＜0时，表示结构处于失效状态；当Z＞0时，表示结构处于可靠状态；当Z=0时，表示结构处于极限状态。

考虑到荷载由永久荷载和可变荷载组成，式（1）的设计表达式可按下式表示：

则计算输电线路元件可靠度的功能函数为

式中：ρ为荷载效应比值；SGK为永久荷载作用效应标准值；SQK为可变荷载作用效应标准值；SG为永久荷载作用效应；SQ为可变荷载作用效应。

2 基本变量的统计分析

2.1 荷载的统计分析

2.1.1 永久荷载的统计参数

输电塔结构永久荷载包括导线及地线、绝缘子及其附件和结构构件及杆塔上各种固定设备等的重力荷载。与一般的民用建筑永久荷载有所差别，GB 50068—2001《建筑结构可靠度统一标准》中永久荷载统计特性是基于民用楼房统计数据得到，若直接引用将有失偏颇。而目前尚无输电塔结构永久荷载统计数据，为此可进行如下处理，杆塔组件自重按式（6）表示：

式中：钢材重度γ以及构件长度l变异性较小，而目前有对钢构件截面几何特性的大量统计，截面特性统计参数均值系数以及变异系数为KA=1.00，VA=0.05。所以自重荷载统计参数主要由截面特性控制，由此取KG=KA=1.00，VG=VA=0.05。

2.1.2 导地线风荷载的统计参数

GB 50545—2010规定，导地线风荷载标准值为：

式中：wx为垂直于导线及地线方向的水平风荷载标准值；α为风压不均匀系数；βc为导线及地线风荷载调整系数；μz为风压高度变化系数；μsc为导线或地线的体形系数；Lp为杆塔的水平档距；θ风向与导线或地线方向之间的夹角；W0为基准风压标准值。参考已有文献［6］，Wx的统计参数计算公式如下：

式中各参数取值见表1。

计算结果为：Kwx=0.467，Vwx=0.410。考虑设计基准期为100年，最大风荷载统计参数分别按KwT=1.154，VwT=0.166计算。

表1 统计参数取值

2.1.3 绝缘子风荷载的统计参数

GB 50545—2010规定，绝缘子风荷载标准值计算公式：

式中：wI为垂直于导线及地线方向的水平风荷载标准值；μz为风压高度变化系数；AI为

绝缘子串承受风压面积计算值；W0为基准风压标准值。

另外，绝缘子的所承受的拉力主要来自导线张力，故绝缘子所承受的总的风荷载为：

假设（dLp）/AI=e，则：

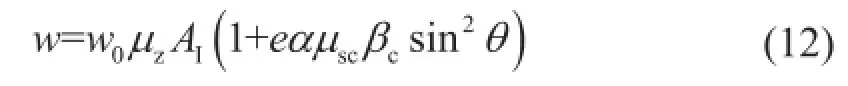
可把比值e看作定值，所以，绝缘子所受风荷载的统计参数（均值系数和变异系数），与导线所受风荷载的统计参数取值相同。

2.1.4 金具风荷载的统计参数

因为金具的所承受的拉力主要来自导线张力，故金具的荷载统计参数取用导地线荷载统计参数。

2.2 抗力的统计分析

2.2.1 导地线抗力的统计参数

由于缺少对导、地线抗力统计分析，考虑导、地线与拉索构件材料性能相似，故参考文献［7］中拉索的统计参数，取三种类型拉索的抗力统计参数平均值：KR=1.28，VR=0.16。

2.2.2 绝缘子抗力的统计参数

本工程所使用的绝缘子含有复合绝缘子、玻璃绝缘子和瓷绝缘子，其中，盘型绝缘子为玻璃绝缘子。绝缘子种类繁多，且不同生产厂家质量水平也不相同，往往是通过试验方法确定绝缘子抗力。由于缺少对绝缘子质量水平统计的资料，因此在进行可靠度分析工作中，参考已有相关研究及其有关文献资料可知：各种绝缘子的机械强度服可用对数正态分布拟合，并且比额定负荷约高出50%，具有较高的机械强度，但强度变异性比较大，在15%～25%。故本文把绝缘子破坏负荷看作其抗力，把其与额定负荷之比m和抗力变异系数当作抗力随机变量，进而分析绝缘子可靠度的变化规律。绝缘子抗力统计参数取值表见表2。

n取值：1.1、1.3、1.5和1.7；

v取值：0.10、0.15、0.20、0.25和0.30。

表2 绝缘子抗力统计参数取值

2.2.3 金具抗力的统计参数

由于有关金具抗力统计资料较为缺乏，考虑到其受力模式与轴心受拉构件较为接近。因此，对金具可靠度，金具抗力统计参数取4种情况均值水平。

根据《架空送电线路杆塔结构设计技术规定》DL 5154—2002，轴心受拉构件的设计表达式为：

式中：N为轴心拉力或轴心压力设计值；m为构件强度折减系数；An为构件净截面面积。对多排螺栓连接的受拉构件，要考虑锯齿形破坏情况，f为钢材的强度设计值。此时，构件抗力R可以表达为

式中：Kp，KA，Kσ分别代表计算模式不确定性、截面几何特性不确定性以及材料强度的不确定性。

根据误差传递公式，此时构件抗力均值系数与变异系数可按下式计算：

根据参考文献［10］，按表3取值。

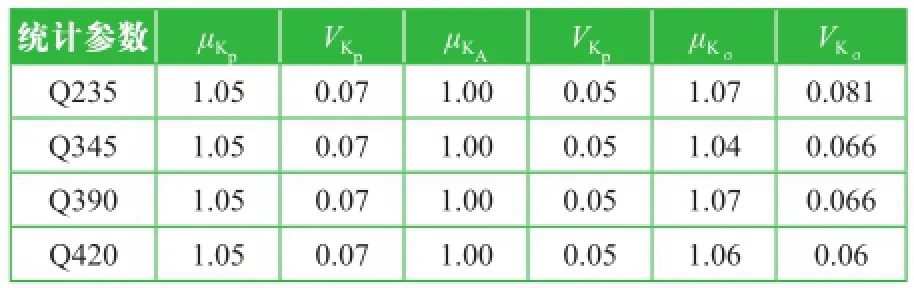
表3 统计参数取值

于是，对于不同种类的钢材，可获得抗拉抗力的统计参数见表4。

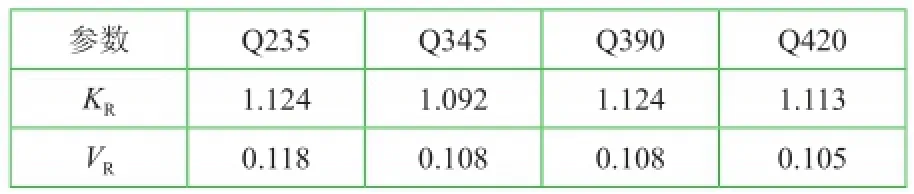
表4 轴心受拉构件抗力的统计参数

随机变量统计参数见表5。

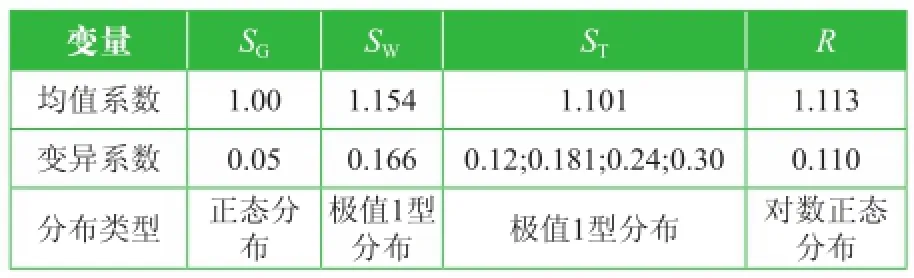
表5 金具随机变量统计参数

3 可靠度分析结果

根据基本变量的统计参数，采用经典的一次二阶矩法计算可靠指标。

3.1 导地线可靠度分析结果

导地线可靠度分析结果见表6，荷载效应比ρ影响见图1。

表6 安全系数Kc取值

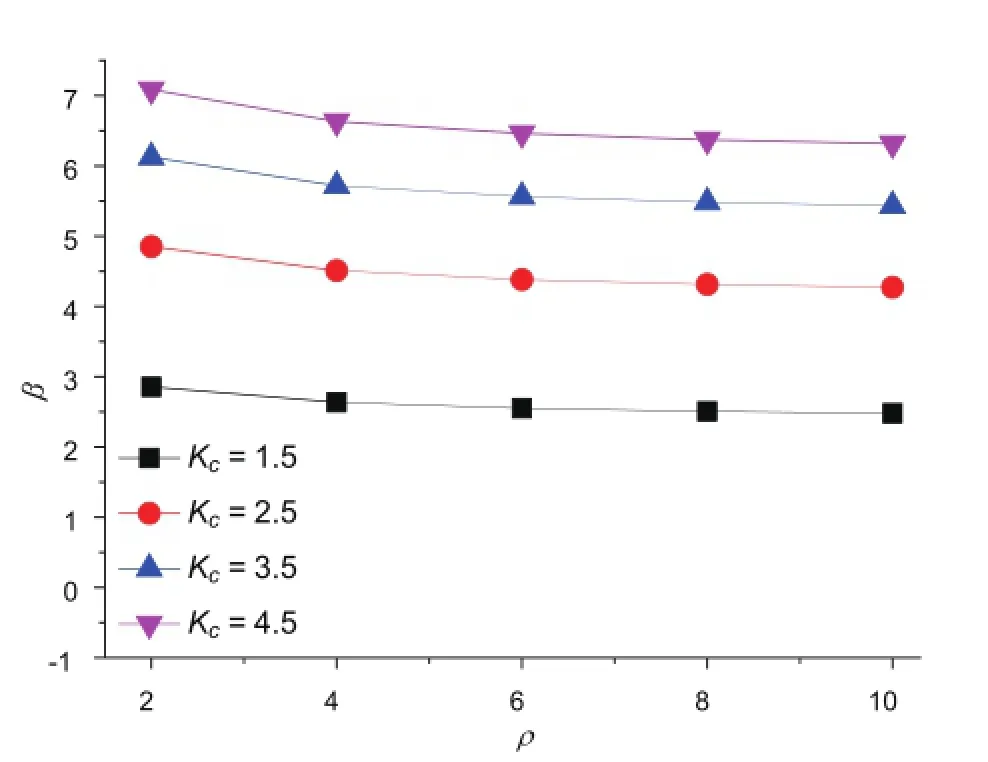
图1 荷载效应比ρ影响

根据上述计算结果可知，随着荷载效应比ρ的递增，导地线的可靠指标不断降低，且随着安全系数的提高，影响逐渐减小。因此，荷载效应比亦是影响导地线可靠指标的主要因素。此外，不难发现，当安全系数取为2.5时，可靠指标均超过4.2。

3.2 绝缘子串可靠度分析结果

绝缘子串可靠度分析结果见图2。

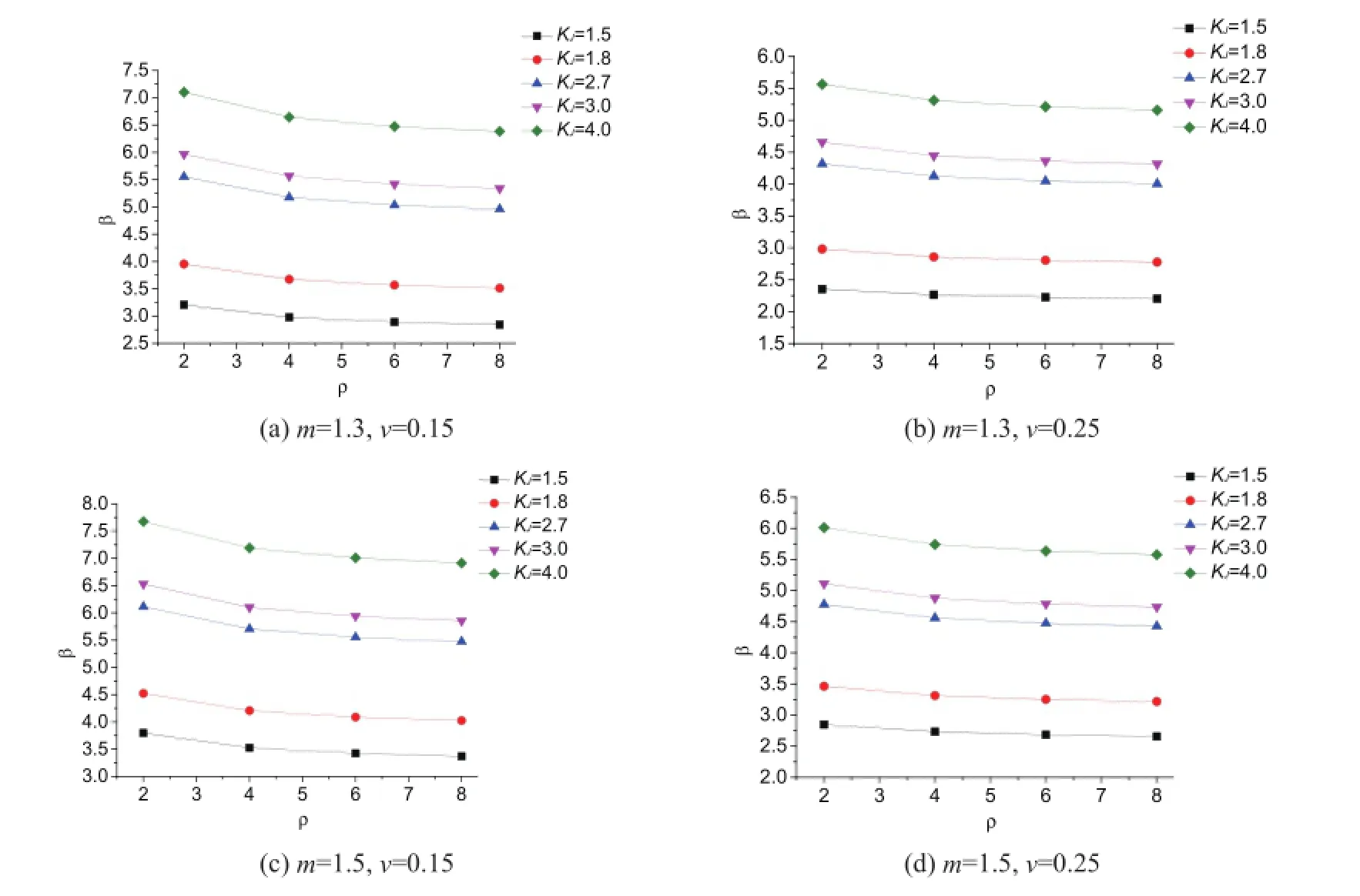
图2 风荷载效应比ρ对可靠指标的影响

与前述构件可靠度的参数分析类似，荷载效应比对于绝缘子的可靠指标亦存在显著影响，属于必须要考虑的因素。且当安全系数取为2.7、m=1.3和v=0.25时，可靠指标均超过4.0。

3.3 金具可靠度分析结果

金具可靠度分析结果见表7和图3。

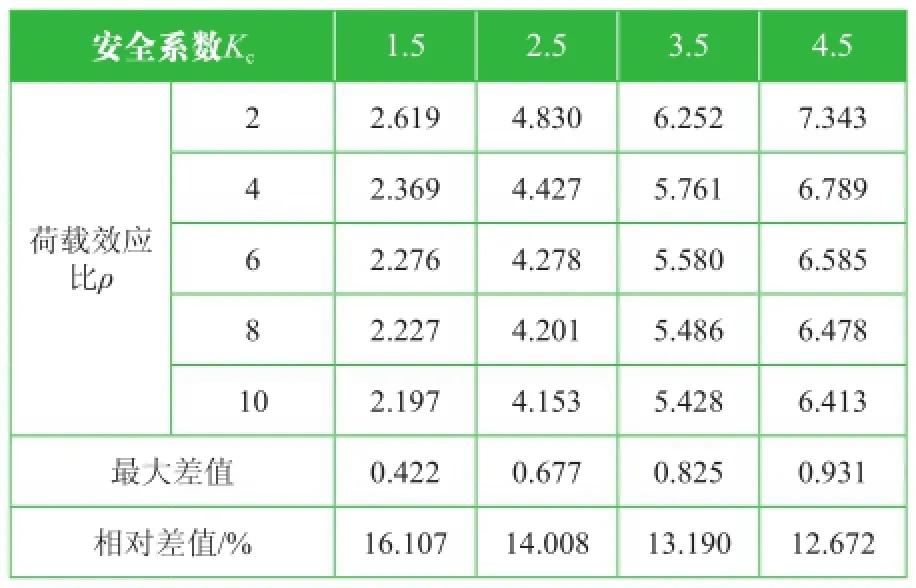
表7 金具可靠指标计算结果

图3 荷载效应比ρ影响

据上述计算结果可知，随着荷载效应比ρ的递增，金具的可靠指标不断降低，且随着安全系数的提高，影响逐渐减小。因此，荷载效应比亦是影响金具可靠指标的主要因素。此外，不难发现，当安全系数取为2.5时，可靠指标均超过4.1。

4 结论

通过建立输电线路元件的极限状态方程，采用一次二阶矩法对输电线路元件的可靠度进行计算分析。得到的主要结论如下：

（1）建立了导地线、绝缘子和金具的极限状态方程。

（2）获得了导地线、绝缘子和金具的荷载统计参数和抗力统计参数。

（3）在现有规范的安全系数下，导地线、绝缘子和金具在大风工况下的可靠度水平均较高，说明现行设计方法是较为安全的。

参考文献：

［1］ 李茂华，李正，杨靖波.特高压输电线路杆塔可靠度研究［J］.电网技术，2010，34（5）.

［2］ 熊铁华，梁枢果，邹良浩.风荷载下输电铁塔的失效模式及其极限荷载［J］.工程力学，2009，26（12）.

［3］ 李致宇.大风覆冰条件下输电杆塔可靠性模型的研究［J］.安全与环境工程，2010，17（3）.

［4］ GB 50545-2010，110 kV～750 kV架空输电线路设计规范［S］.

［5］ GB 50068-2001，建筑结构可靠度统一标准［S］.

［6］ 欧进萍，段宇博.等效随机静风荷载的模型及其参数确定［J］.哈尔滨建筑工程学院学报.1994，27（2）.

［7］ 杨会杰，陈志华.预应力钢结构拉锁抗力的统计分析［C］.第七届全国现代结构工程学术研讨会，工业建筑，2007.

［8］ 邱志贤.绝缘子电气机械特性的数理统计研究［J］.电磁避雷器，1976，（3）.

［9］ 张伟，等.基于概率统计的盘型悬式瓷绝缘子抽检方法［J］.内蒙古电力技术，2011，29（4）.

［10］ 夏正中，钢结构可靠度分析［J］.工业建筑，1981，（12）.

中图分类号：TM75

文献标志码：B

文章编号：1671-9913（2016）01-0058-05

* 收稿日期：2015-04-28

作者简介：徐彬（1987- ），男，湖北洪湖人，硕士，工程师，主要从事输电线路结构和基础设计研究工作。

Structural Reliability Analysis of Transmission Line Elements

XYU Bin， WANG Song-tao， ZENG Er-xian， WU Hai-yang
（Central Southern China Electric Power Design Institute， Wuhan 430071， China）

Abstract:For the correct evaluation of the safety of the transmission line， taking the transmission line elements （conductor & earth wire， insulator and hardware） as the analysis objects， the reliability analysis model was established，by analyzing the affecting factors of load effect of transmission line elements such as the calculation formula and distribution curve of permanent load and wind load， the statistical parameters of load effect were obtained； Considered the uncertainty of material properties， geometry and computational model， the resistance statistical parameters were obtained. Using a second-order moment method， calculated the reliability index of the transmission line element in maximum wind condition .Results show that the reliability level of the transmission line elements designed by current specification of safety factor was high. The calculation results can provide reference for the establishment of probability limit state design methods of the transmission line.

Key words:transmission line； elements； reliability index.