基于罚函数的设施定位布置问题模型与算法

罗蓉娟，戢守峰　

（东北大学　工商管理学院，辽宁　沈阳　110167，E-mail：sfji@mail.neu.edu.cn）

基于罚函数的设施定位布置问题模型与算法

罗蓉娟，戢守峰

（东北大学工商管理学院，辽宁沈阳110167，E-mail：sfji@mail.neu.edu.cn）

摘要：针对系统内部设施布置决策，以定位布置问题为研究对象，提出了一种求解该问题的改进分布估计算法（IEDA）。通过分析定位布置问题的基本特征，建立了带容量约束的基本非线性整数规划模型；引入了基于罚函数的约束处理方法建立了定位布置问题的改进数学模型，进而使用带惩罚项的目标函数引导IEDA的搜索方向；在IEDA中融入了一种概率矩阵变异机制和基于互换型邻域结构的局部搜索策略，用于平衡算法的全局和局部搜索能力；并通过仿真实验比较和对某建筑工地实例求解验证了模型的合理性与算法的有效性。

关键词：定位布置问题；分布估计算法；罚函数；仿真实验

设施布置问题（Facility Layout Problem，FLP）是对生产系统内部各设施进行优化布局，以提高企业的长期经济效益。作为一类典型的组合优化问题，设施布置问题需要考虑决策目标、设施特征、物料搬运过程及场地物理空间等诸多因素，其决策过程十分复杂［1］。依据生产系统内部的作业流程特征，基本设施布置形式可以分为按产品原则布置、按工艺过程原则布置、成组技术与定位布置等，选择合理的设施布置形式已经成为影响企业运营效率的关键因素。定位布置问题（Fixed-Positioning Layout Problem，FPLP）的研究对象为单个中心设施/位置（Hub Facility/Position，HF/P）和多个外围设施/位置（Peripheral Facility/Position，PF/P）所构成的系统。通常，中心设施体积较大或质量较重且不易挪动，外围设施需要按照一定的规则围绕中心设施进行布置，决策目标为最小化总物流费用。定位布置问题广泛存在于建筑施工、筑路、造船和飞机制造等实际生产制造系统中，已经成为企业运营管理领域的技术热点之一［2，3］。

理论上，如果将外围设施围绕中心设施作同心圆布置，则各外围设施与中心设施之间的物流费用总和为固定值，此时定位布置问题可抽象为一类特殊（即目标函数包含常数项，且带附加约束条件）的二次分配问题（Quadratic Assignment Problem，QAP）［4］。实际上，由于受到作业场地面积和形状的限制，使得可利用的位置到中心设施的距离不尽相同，无法保证外围设施与中心设施间的同心圆布置。因此，定位布置问题不仅需要考率多个外围设施间的物流费用总和，而且要考虑各个外围设施与中心设施之间的物流费用总和，同时还需考虑位置容量约束的硬约束条件（即不允许松弛到目标函数中）。可知，定位布置问题属于典型的约束组合优化问题，且二次分配问题可以归约为定位布置问题，其求解难度比二次分配问题复杂得多，属于组合优化问题中的NP-难范畴，无法在多项式时间内获得大规模问题的最优解［5］。目前，使用基于智能优化的方法，求解特定指标下的生产系统内部设施布置问题已经成为学术界的研究热点。如Pourvaziri等［6］提出了一种混合多种群遗传算法用于求解动态设施布置问题，并把解空间划分成多个独立的部分用于保持算法多样性，融入了一种基于模拟退火的局部搜索以提高算法搜索能力。García-Hernández等［7］在处理不等面积设施布置问题时，把决策者的干预加入到了遗传算法中，以此来调整算法的参数设置，进而实现算法与专家决策的交互作用。Guan等［8］把一种基于变邻域搜索的蚁群算法用于单列设施布置问题的优化中，使用 60组标准测试算例对算法的性能进行了验证。根据文献调研，使用智能优化算法求解设施定位布置问题尚无文献报道，因此设计和开发有效的智能优化算法求解设施定位布置问题具有一定的意义。

1　定位布置问题的数学模型

1.1问题描述

定位布置问题即在中心设施位置固定的情况下，外围设施围绕中心设施进行布置，通过对外围设施布置方案进行优化调整实现目标函数（总物流费用）的最小化。由于外围与外围设施、外围与中心设施之间均存在着复杂的物料搬运关系，因此不仅需要考虑外围设施间的物流费用和对总物流费用的影响，同时还需考虑各外围设施与中心设施间的物流费用和对总物流费用的影响。此外，实际作业场地的可利用空间往往是有限的，必须考虑位置容量这一硬约束条件。可见，定位布置问题属于典型的约束优化问题，其求解难度受到问题规模与约束松紧的双重影响，因此需要在基本数学模型的基础上建立基于约束处理技术的改进数学模型。

1.2基本数学模型

参数：cij为设施i与j之间的物流量；dkl为位置k与l之间的距离；hi为设施i到中心设施的物流量；gk为位置k到中心位置的距离；qi为设施i的空间占用量；Qk为位置k的容量；

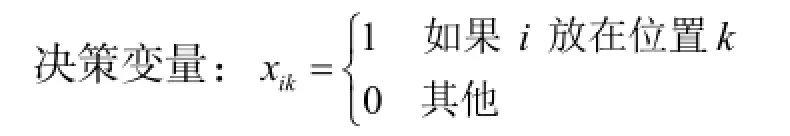
基于上述参数和决策变量，定位布置问题的目标函数和约束条件如下：

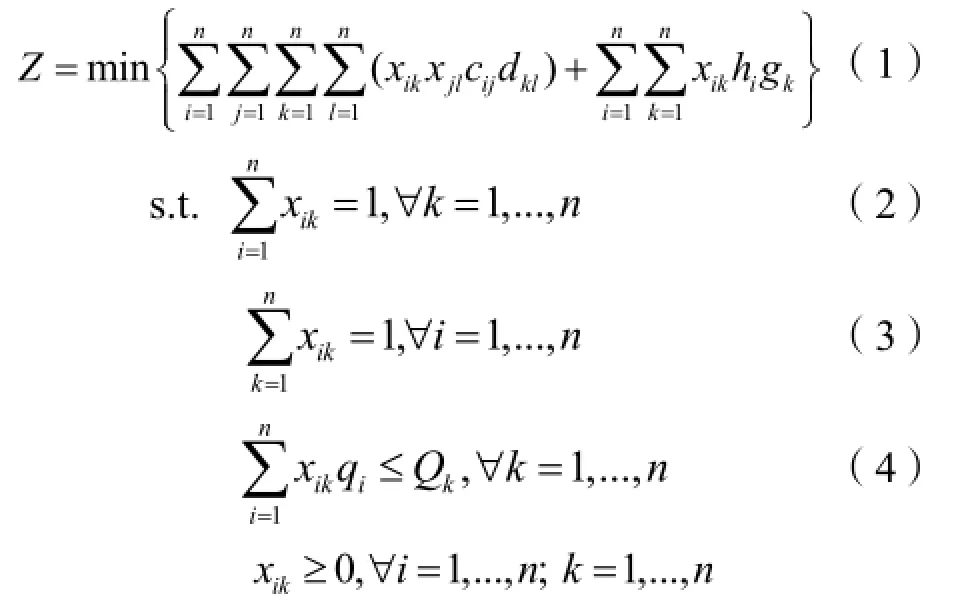
其中，式（1）为目标函数（即总物流费用），前项表示外围设施之间的物流费用和，后项表示各个外围设施到中心设施的物流费用和；式（2）和（3）为指派类约束，其中式（2）表示每个设施只能放置在一个位置上，式（3）表示每个位置上只能放置一个设施；式（4）为容量约束，表示所放置设施的空间占用量总和不能超过相应位置的容量。

1.3基于罚函数的改进数学模型

由于上述基本数学模型中容量约束的存在，要求智能优化算法在搜索过程中必须兼顾解的可行性和质量，因此需要引入恰当的约束处理技术。目前，主流的智能约束处理技术主要包括罚函数［9］，基于排序的方法［10］、基于多目标的方法［11］等。其中，罚函数法是最简单有效的约束处理技术，对问题结构没有硬性要求且简单易于实现［12］，本文采用基于罚函数的方法把容量约束（式（4））附加惩罚权重后追加到原目标函数中，定位布置问题的改进数学模型如下：

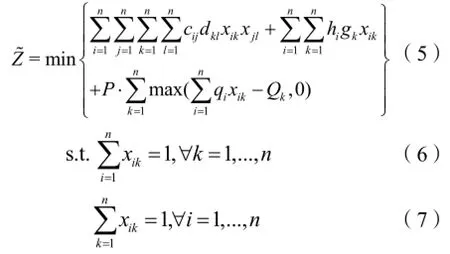
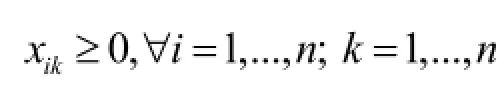
其中，式（5）为引入惩罚项后的新目标函数，最后一项为惩罚项，P表示罚因子。

2　改进分布估计算法设计

分布估计算法（Estimation o f D istribution A lgorithm，EDA）是一种基于概率模型的随机优化方法，在求解规模较大和复杂度较高的组合优化问题中效果显著［13］。EDA通过对概率模型进行更新和采样形成新的个体，与遗传算法相比，能较好地把握宏观搜索方向，具有较强的全局搜索能力，但局部搜索能力较差［14］。针对这一特点，所提出的改进分部估计算法（Improved Estimation of Distribution A lgorithm，IEDA）加入了一种基于邻域互换型的局部搜索机制，用于提高算法的搜索深度，同时采用了一种概率矩阵扰动机制来拓展算法的搜索宽度。

2.1编码策略

根据定位布置问题的特征，采用基于设施编号的方法进行编码，由于中心设施位置已知，故只需使用外围设施字符排列来表示可行的布置方案。如，π=［4，3，2，5，1］表示设施4放在位置1，设施3放在位置2，设施2放在位置3，设施5放在位置4，设施1放在位置5。

2.2随机种群初始化

为了防止算法在迭代寻优过程中陷入局部最优，需要保持初始解在解空间中的均匀分布。因此，IEDA采用随机初始化种群的方法，即随机生成的popsize个体组成初始种群，作为算法搜索的起点。

2.3概率矩阵初始化

EDA使用概率矩阵来记录进化过程中优质解的历史信息，从而有效指导算法的搜索方向。概率模型的选择需要结合问题的结构特征。由于定位布置属于离散型组合优化问题，故IEDA使用概率矩阵作为概率模型。则算法在第gen代的概率矩阵定义为：

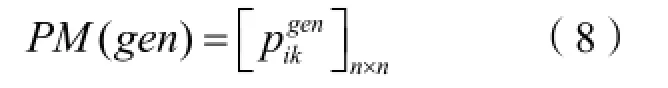
其中，该概率矩阵满足列归一性，即：

2.4概率矩阵更新机制

为了使算法获得较快的收敛速度并提高搜索效率，IEDA采用历史最优个体对概率矩阵进行更新。设表示第gen代的历史最优个体（best so far），LR表示学习速率，则概率矩阵的更新步骤如下：

步骤1：令j=1；

步骤4：令j=j+1，如果j≤n，转向步骤2；

步骤5：输出PM（gen+1）。

2.5概率矩阵采样机制

IEDA通过概率矩阵采样生成新一代种群。本文采用基于轮盘赌的采样操作既利用了概率矩阵的信息，有利于保证较好的位置以较大的概率被选中。在采样的过程中，按照从左到右的顺序进行采样，当位置j选中设施F后，设置n）以保证解的可行性。

设 πi,gen+1表示种群 πgen+1中的第 i个个体，SelectFaclity（πi,gen+1（j））=F表示个体 πi,gen+1中的第 j个位置选中设施F的函数，则SelectFaclity（πi,gen+1（j））的步骤如下：

步骤1：构造轮盘赌；

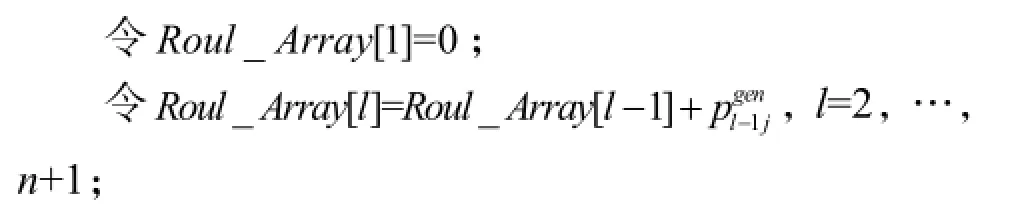
步骤2：选择设施F；

产生随机小数R∈［0，1）；

步骤3：输出F。

根据上述步骤，IEDA的采样操作步骤如下：

步骤1：令i=1；

步骤2：令j=1；

步骤4：j=j+1，若j≤n，转向步骤3；

步骤5：令i=i+1，若i≤popsize，转向步骤2；

步骤6：输出πgen+1。

2.6概率矩阵变异机制

为了保持种群的多样性，提高算法的搜索宽度，IEDA引入了概率矩阵变异机制。设 Pmu为变异概率，MR为变异速率。变异步骤如下：

步骤1：令j=1；

步骤3：如果R＞Pmu，则并转向步骤6；

步骤6：令j=j+1，如果j≤n，转向步骤2；

步骤7：输出PM（gen）。

2.7基于互换型邻域结构的局部搜索

组合优化问题的近邻假设理论认为，在较好解的附近一般也存在较好的解，为了利于算法在相对狭窄的局部解空间周围发现更优良的解，引入了基于互换型（Interchange）邻域结构的局部搜索策略。同时，为了防止算法因过度的局部搜索而陷入局部最优，EDA采用了首次改进跳出原则。

2.8IEDA的算法流程

设genMax为 IEDA的最大迭代次数，结合上述相关操作，IEDA的算法流程如图1所示。

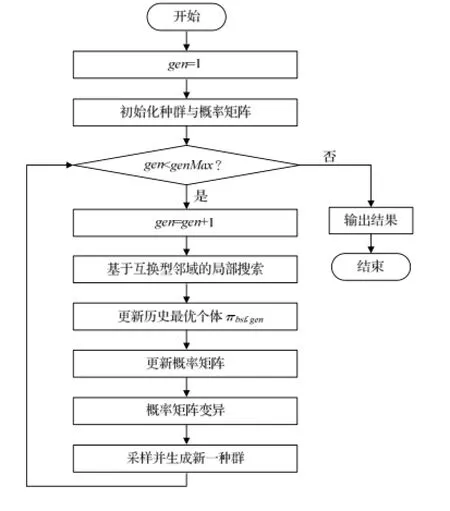
图1　　IEDA的算法流程图　

3　仿真实验比较和实例求解

3.1实验设置

由于目前尚不存在针对定位布置问题的benchmark算例，随机生成了20组不同规模的算例为测试对象，算例规模（即外围设施/位置数目）分别为：5，8，9，10，13，15，18，20，23，25，28，30，33，35，38，40，43，45，48，50。模型中参数的生成规则如下：cij∈U［1，100］，dkl∈U［1，100］，h1∈U［1，100］，gk∈U［50，100］，qi∈U［1，50］，其中，

所有算法使用 M icrosoft Visual Studio2008 （C++语言）编程实现，实验硬件环境为Core i53.3GHz，RAM3.46GB；软件环境为，Windows7。所有的算法都独立重复运行 21次，采用目标函数平均值（AOV），约束违反量平均值（ACV）及可行率（FR）［15］作为评价指标来衡量算法的性能。显然，AOV可以作为算法寻优能力的衡量尺度，ACV和FR可以用于衡量算法的约束处理能力。IEDA的参数配置为：popsize=50，LR=0.02，Pmu=0.05，MR=0.005，P=1000000。

3.2算法性能比较分析

为了所提出的IEDA的有效性，考虑将IEDA与下列算法进行比较：①PEDA：标准分布估计算法（Pure Estimation of Distribution A lgorithm，PEDA），即其操作中不包含概率矩阵变异操作和局部搜索操作，其余操作及参数配置与IEDA相同；②PEDA_LS：在PEDA中加入局部搜索操作，其余操作及参数配置与PEDA相同；③GA：标准遗传算法（Genetic A lgorithm，GA），采用基于轮盘赌的选择方法，变异概率和交叉概率分别取0.3和0.7，种群规模为50；④GA_LS：在GA中融入局部搜索操作，其余操作及参数配置与GA相同。

为了保证算法性能比较实验的公平性，设置所有EDA类算法均运行1000代，而GA和GA_LS均运行15000代，按照实验设置规则运行所有算法所得到的实验结果如表1所示。同时，对IEDA，GA和GA_LS3种算法的平均运行时间进行了统计，其结果如图2所示。

由表1可知，IEDA和PEDA_LS明显占优于其他3种对比算法，表明EDA类算法在求解定位布置问题时具有明显优势，同时也验证了所设计的基于互换型邻域的局部搜索策略是有效的。虽然IEDA与PEDA_LS在AOV指标上没有显著差异，但IEDA解的FR高于PEDA_LS，这表明所设计的概率矩阵变异策略有利于提高IEDA的约束处理能力。值得注意的是，IEDA的FR平均水平几乎达到了100%，表明IEDA在求解带容量约束的定位布置问题时具有较高的可靠性。

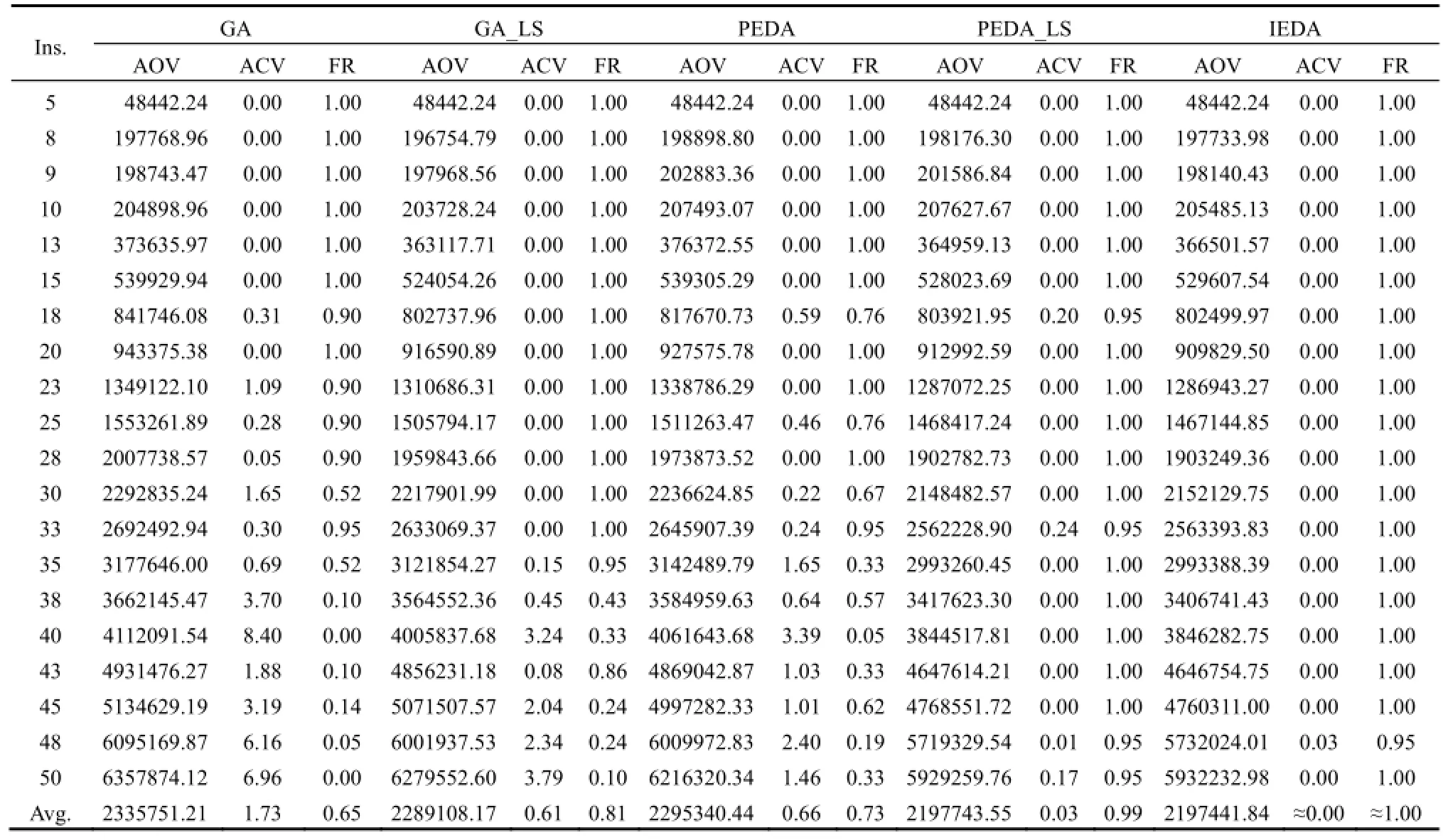
表1　　算法性能比较结果　

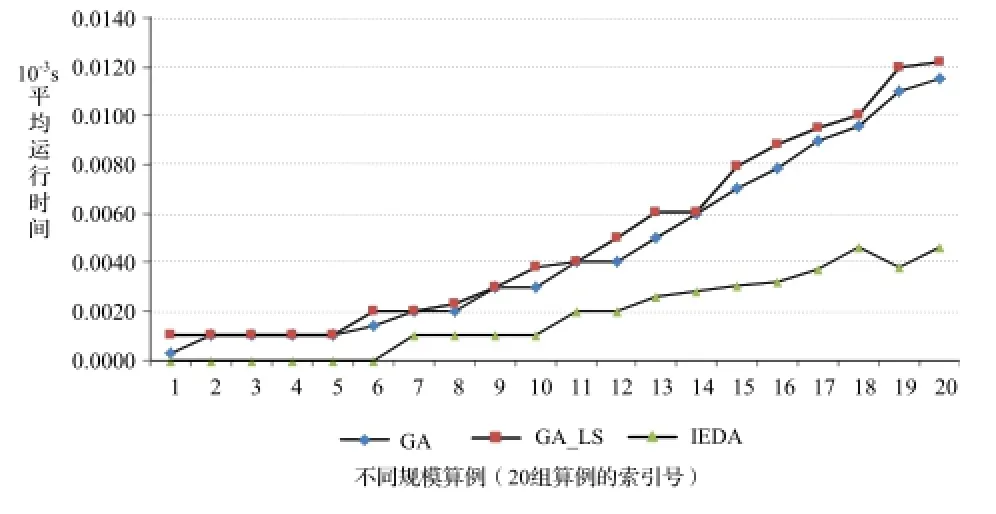
图2　　算法运行时间趋势图　

由图2可知，虽然IEDA的运行代数要远小于GA和GA_LS，但对所有的算例，IEDA都能在较短的时间内获得优质的解，说明IEDA具有较高的搜索效率。

3.3实例求解

以沈阳市某建筑物施工现场为例，验证模型的合理性与算法的有效性。该建筑工地内的主要外围功能设施有：螺纹钢库、线材库、钢管库、石子库、木枋库、沙场、砌砖块库、水泥库、钢筋加工区、钢筋成品库（I）、钢筋成品库（II）、石粉碎区、混凝土加工区、砌砖加工区和模板加工区等 15个可利用位置。

根据实际施工过程中的工艺需求，测算出各个外围设施之间的距离及物流量矩阵、中心物流量、中心距离、设施的空间占有量和位置容量，统计结果如表2和表3所示。

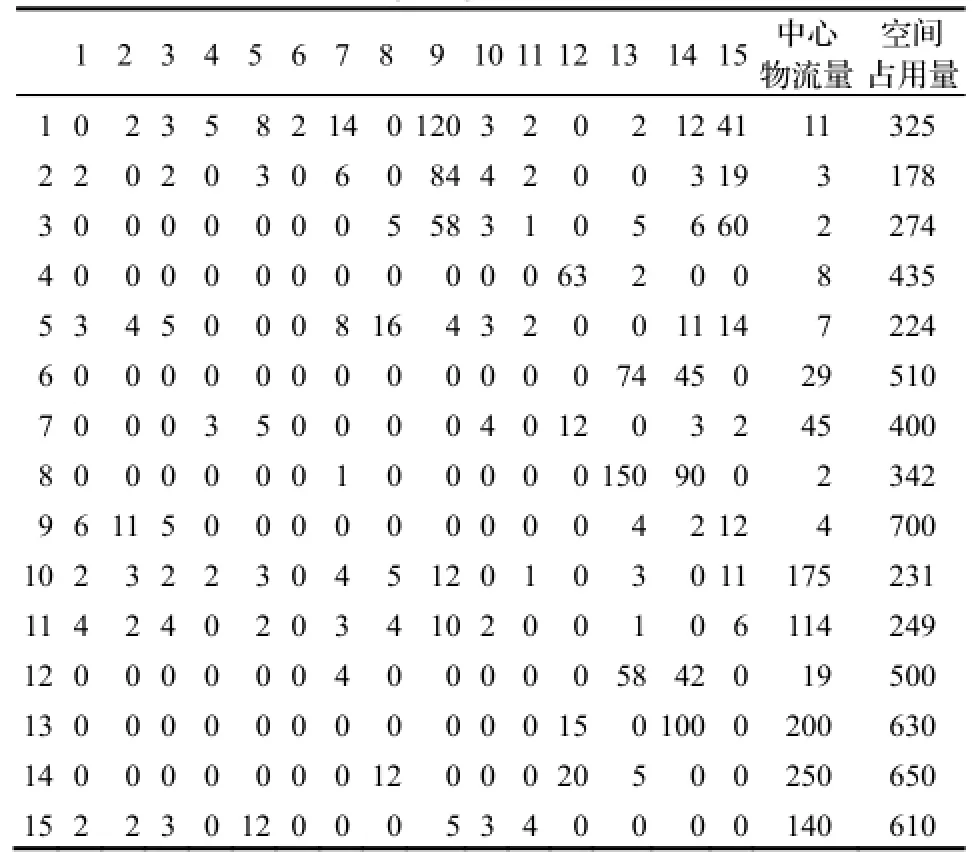
表2　　物流量矩阵、中心物流量及空间占用量　

根据以上数据信息，使用IEDA算法独立重复运行21次，所得结果如表4所示。

由上述求解结果可知，IEDA能够在0.1s的时间内获得最优解，而且在算法独立重复运行 21次时，可行率为100%，再次验证了IEDA的有效性以及在实际工程中的可用性。

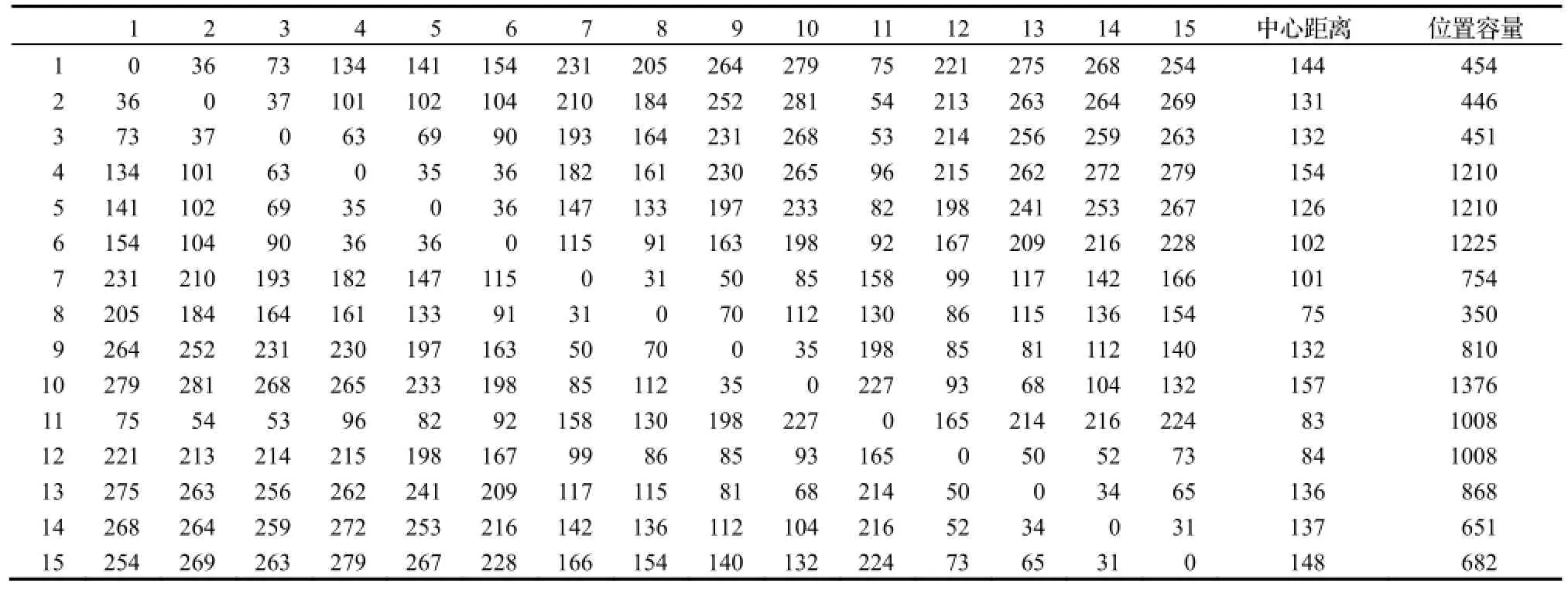
表3　　物流量矩阵、中心距离及位置容量　

表4　　IEDA优化性能分析　

4　结语

本文针对最小化总物流费用指标下的定位布置问题，提出了一种改进分布估计算法（IEDA）进行求解。根据定位布置问题的特征，构建了该问题的基本非线性整数规划模型；使用基于罚函数的方法对容量约束进行处理，并提出了该问题的改进数学模型；在IEDA中融入了一种概率矩阵变异机制和基于互换型邻域结构的局部搜索策略，用于平衡算法的全局和局部搜索能力；并通过仿真实验比较和基于建筑工地的实例求解对IEDA的性能及工程价值进行了验证。进一步将针对多目标的设施布置问题进行研究，使用基于 EDA的混合算法求解更复杂情况下的设施布置问题。

参考文献：

［1］周志文.生产与运作管理［M］（第1版）［M］.北京：石油工业出版社，2001.

［2］戢守峰.现代设施规划与物流分析（第一版）［M］.北京：机械工业出版社，2013.

［3］王晶.生产与运作管理（第一版）［M］.北京：清华大学出版社，2011.

［4］Lee H Y，Kang S，Chae J.Mutation effects in a genetic algorithm for a facility layout problem in QAP form［J］.International Journal of Advanced Logistics，2015，4 （3）：170-179.

［5］张鸿宾.组合优化问题的启发式搜索［J］.计算机科学，1998，25（2）：13-16.

［6］Pourvaziri H，Naderi B，Pourvaziri H，et al.A hybrid multi-population genetic algorithm for the dynamic facility layout problem［J］.Applied Soft Computing，2014，24 （24）：457-469.

［7］García-Hernández L，Palomo-Romero J M，Salas-M orera L，et al.A novel hybrid evolutionary approach for capturing decision maker know ledge into the unequal area facility layout problem［J］.Expert Systems with Applications，2015，42（10）：4697-4708.

［8］Guan J，Lin G.Hybridizing variable neighborhood search w ith ant colony optim ization for solving the single row facility layout problem［J］.European Journal of Operational Research，2016，248（3）：899-909.

［9］Liu J，Teo K L，Wang X，et al.An exact penalty function-based differential search algorithm for constrained global optim ization［J］.Soft Computing，2015：1-9.

［10］Ho P Y，Shimizu K.Evolutionary constrained optimization using an addition of ranking method and a percentage-based tolerance value adjustment scheme［J］.Information Sciences（S0020-0255），2007，177（14）：2985-3004.

［11］Wang Y，Caiz X，Guo G Q.Multi objective optimization and hybrid evolutionary algorithm to solve constrained optim ization problem s［J］.IEEE Trans on Systems，Man and Cybernetics-Part B：Cybernetics（S1083-4419），2007，37（3）：560-575.

［12］王凌，何锲，金以慧.智能约束处理技术综述［J］.化工自动化及仪表，2008，35（1）：1-7.

［13］Hauschild M，Pelikan M.An introduction and survey of estimation of distribution algorithms［J］.Sw arm&Evolutionary Computation，2011，1（3）：111-128.

［14］王圣尧，王凌，方晨，等.分布估计算法研究进展［J］.控制与决策，2012，27（7）：961-966.

［15］Mallipeddi R，Suganthan P N.Problem definitions and evaluation criteria for the CEC2010Competition on Constrained Real-Parameter Optimization［R］.Singapore：Nanyang Technological University，2010.

辽宁省教育厅人文社科基地项目（ZJ2013014）.

中图分类号：TU731

文献标识码：A

文章编号：1674-8859（2016）03-116-06

DOI：10.13991/j.cnki.jem.2016.03.020

作者简介：

罗蓉娟（1992-），女，硕士研究生，研究方向：设施布置理论与智能优化；

戢守峰（1958-），男，教授，博士生导师，研究方向：物流系统建模与优化，物流与供应链管理。

收稿日期：2016-04-02.

基金项目：国家自然科学基金项目（71572031）；

M odel and A lgorithm for Fixed-positioning Layout Based on Penalty Function

LUO Rong-juan，JI Shou-feng
（School of Business Administration，Northeastern University，Shenyang110167，China，E-mail：sfji@mail.neu.edu.cn）

Abstract：Considering the decision of interior facility layout in the production systems and aiming at facility layout problem，an improved estimation of distribution algorithm（IEDA）is given to solve this problem.Firstly，based on its essential characteristics，a nonlinear integer programm ing model w ith capacity constraints is established to formulate associated basic properties.Secondly，a modified mathematical model combining w ith the penalty function based constraint handling method is constructed，w hich indicates that if the capacity constraint of any position is not satisfied，the related penalty term w ill be set to a high punishment，otherw ise set to zero.And thereafter，the objective function with penalty terms is used to guide the search direction of our proposed IEDA.Thirdly，a mutation mechanism for probability matrix and an interchange-based local search w ith first move strategy are embedded into IEDA to balance the global and local search ability.Finally，the results of simulation experiments and case study from a construction site demonstrate the rationality of the model and the effectiveness of the presented IEDA.

Keywords：fixed-positioning layout problem；estimation of distribution algorithm；penalty function；simulation experiments