潜水的非稳定运动理论在水库渗漏量计算中的应用

郭印亮

（河北省水利水电勘测设计研究院，天津　300250）



潜水的非稳定运动理论在水库渗漏量计算中的应用

郭印亮

（河北省水利水电勘测设计研究院，天津300250）

摘 要：新建一个水库工程前，一般都要对水库的坝址、库容、渗漏、浸没、库岸稳定等问题进行研究、分析，并给出评价结论。其中，水库渗漏、浸没问题影响到水库的效益、周围的生态环境及建筑物安全。详细介绍了地下水动力学原理在水库浸没范围预测及渗漏量估算中的应用。

关键词：地下水动力学；水库；浸没；渗漏量

1　水库渗漏及浸没的概念

水库渗漏包括暂时性渗漏与永久性渗漏。暂时性渗漏是指水库蓄水初期为了饱和库水位以下岩土体的孔隙、裂隙和空洞而出现的库水损失，这部分渗漏损失是所有水库都有的暂时现象，不影响水库永久性蓄水和正常运行，一般不作专门研究。永久性渗漏是指库水沿着透水的岩土体或构造流向库外的邻谷、洼地或坝下游区域而形成的渗漏现象，这种渗漏是长期的，直接影响水库的蓄水效益。一定时间段内的渗漏量与渗透途径的岩土体的透水性、渗径长短及水头大小有关，永久性渗漏是水库渗漏问题研究的重点。

水库浸没是指水库蓄水后水库周围地下水位抬高，导致地面盐渍化、沼泽化、建筑物地基条件恶化等现象。在丘陵地区、山前洪积扇及平原区修建水库，由于水库周围地势低缓，岩土体具有一定的透水性，很容易发生浸没现象，且范围很大。水库浸没问题有时会影响到蓄水位及坝址的选择。

2　水库渗漏量的计算

2.1假定条件

（1）含水层为均质各向同性且无限延伸，位于水平隔水层以上。

（2）水库蓄水前的地下水潜水位近水平，水力坡度为零。

（3）水库连续快速蓄水至正常蓄水位，上升幅度为Δh0,t，且上升后蓄水位保持不变，可按式（1）计算。

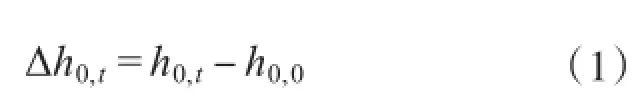
式中∶h0,t为自起始时刻水位抬升至t时刻到达的水位（m）；h0,0为起始时刻对应的水位（m）。

（4）计算坝基渗漏量时，库水在坝基岩土体的渗漏看作一维流。

（5）蓄水位变幅不大于0.1～0.2倍的潜水流厚度。

（6）正常蓄水位与岸边或坝体相交处对应的渗漏计算断面为起始断面0，沿渗流方向距起始断面0的距离为x的断面为渗漏计算断面x，t时刻断面x的水位为u（x,t）。

2.2计算公式

u（x,t）计算公式为：

式中：u（x,t）为距起始渗漏断面0距离为x、时间为t时的断面x水位（m）；F（λ）为与x、t及压力传导系数a有关的系数，查表确定；a为压力传导系数（m2/d），a=k×hm/μ；μ为潜水含水层的给水度；hm为潜水流平均厚度（m）；k为岩土体渗透系数（m/d）。

根据达西定律，渗透流速v=kI，经推导可得到：

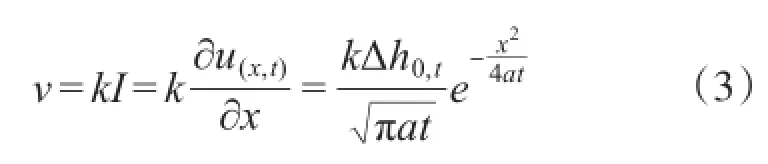
式中：v为任意时刻t（d）、至起始断面0距离为x（m）处的渗透流速（m/d）；k为渗透系数（m/d）；I为水力比降，即沿水流方向单位长度上的水头差（m）；u（x,t）为距起始渗漏断面0距离为x、时间为t时的断面x水位（m）；Δh0,t为t=0时刻水库水位连续快速上升至正常蓄水位时的上升幅度（m）；a为压力传导系数（m2/d），a=k×hm/μ；μ为潜水含水层的给水度；hm为潜水流平均厚度（m）。

根据式（3），可得单宽流量的计算公式：

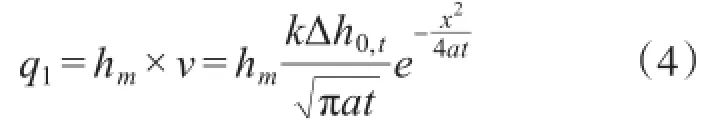
式中：q1为单宽流量（m3/d）；hm为潜水流平均厚度（m）；v为任意时刻t（d）、至起始断面0距离为x（m）处的渗透流速（m/d）；k为渗透系数（m/d）；Δh0,t为t=0时刻水库水位连续快速上升至正常蓄水位时的上升幅度（m）；a为压力传导系数（m2/d），a=k×hm/μ；μ为潜水含水层的给水度。

由式（4）可知：

（2）同一断面单宽流量随时间的增大而逐渐减小。

（3）水库蓄水后时间t内起始断面0处的单宽渗漏量Vt可按式（5）计算。

式中：Vt为水库蓄水后时间t（d）内起始断面0处的单宽渗漏量（m3）；hm为潜水流平均厚度（m）；k为渗透系数（m/d）；Δh0,t为t=0时刻水库水位连续快速上升至正常蓄水位时的上升幅度（m）；a为压力传导系数（m2/d），a=k×hm/μ；μ为潜水含水层的给水度。

3　水库浸没范围的预测

水库蓄水后将引起水库周围潜水位升高，当潜水位升高达到地下水埋深临界值Hcr时将形成库区周围的浸没现象。地下水埋深临界值Hcr可按式（6）计算。

式中：Hk为土的毛细管上升高度（m）；ΔH为安全超高值（m）。

hx,t的计算公式为：

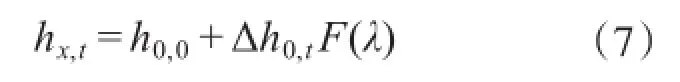
式中：hx,t为某一时刻t（d）不同断面x（m）处的潜水位（m）；h0,0为潜水位（m）；Δh0,t为t=0时刻水库水位连续快速上升至正常蓄水位时的上升幅度（m）；F（λ）为与x、t及压力传导系数a有关的系数，查表确定；a为压力传导系数（m2/d），a=k×hm/μ；μ为潜水含水层的给水度；hm为潜水流平均厚度（m）；k为岩土体渗透系数（m/d）。

式（7）中，潜水位h0,0、库水位的上升幅度Δh0,t是确定的，根据式（6）可以确定断面x处发生浸没时地下水埋深临界值对应的hx,t值，根据式（7）可求出F（λ）值，根据 F（λ）值查表取得 λ值。根据λ=及至初始断面0的距离x，可以计算达到浸没状态的时间t。实例，见表1。

表1　计算x=100 m处发生浸没时所需时间

利用式（7），可以计算出某一时刻t不同断面x处的潜水位hx,t，将其连成一条光滑的曲线，即为该时刻的浸润曲线。当潜水位高于或等于地下水埋深临界值时即发生浸没。实例，见表2。

表2　判定t=365 d时x=80 m处是否发生浸没

4　结论

（1）本文利用潜水的非稳定运动理论，提供了渗流出逸点未知时的一种渗漏量计算方法。这种计算方法对坑塘蓄水及沟渠灌溉工程潜水流含水层比较均匀时引起的渗漏量计算及浸没范围预测较为准确。

（2）对于水库渗漏及浸没问题，当含水层比较均匀且厚度为蓄水位变幅的5～10倍时，可对水库渗漏量进行估算及预测水库浸没范围。

参考文献

［1］薛禹群.地下水动力学原理［M］.北京：地质出版社，1986.

中图分类号：TV697.2+1

文献标识码：A

文章编号：1004-7328（2016）01-0044-02

DOI：10.3969/j.issn.1004-7328.2016.01.016

收稿日期：2015—10—10

作者简介：郭印亮（1969—），男，高级工程师，主要从事岩土工程勘察工作。