自适应蚁群算法在TSP问题中的应用与研究
2016-07-28贾丽媛周翠红湖南城市学院湖南益阳413000
贾丽媛,周翠红(湖南城市学院,湖南 益阳 413000)
自适应蚁群算法在TSP问题中的应用与研究
贾丽媛,周翠红
(湖南城市学院,湖南 益阳 413000)
摘 要:传统算法在构造解的过程中,利用随机选择策略,这种选择策略使得进化速度较慢,正反馈原理旨在强化性能较好的解,却容易出现停滞现象。这是造成蚁群算法的不足之处的根本原因.因而我们从选择策略方面进行修改,我们采用确定性选择和随机选择相结合的选择策略,并且在搜索过程中动态地调整作确定性选择的概率当进化到一定代数后,进化方向已经基本确定,这时对路径上信息量作动态凋整。缩小最好和最差路径上的信息量的差距,并且适当加大随机选择的概率,以小于 l对解空间的更完全搜索,从而可有效地克服基本蚁群算法的不足,此算法属于自适应算法。
关键词:蚁群算法;自适应函数;全局优化;函数优化
在二十世纪九十年代初期,意大利M.Dorigo,V.Maniezzo,A.Colorni[1]等人首先提出了一种新的启发式优化算法,又叫蚁群系统(Ant Colony System),这种算法是目前国内外启发式算法中的研究热点和前沿课题,被成功地运用于旅行商问题的求解,蚁群算法在求解复杂优化问题方面具有很大的优越性和广阔的前景。但是,根据观察实验发现,蚁群中的多个蚂蚁的运动是随机的,在扩散范围较大时,在较短时间内很难找出一条较好的路径,在算法实现的过程中容易出现停滞现象和收敛速度慢现象。在这种弊端的情况下,学者们提出了一种自适应蚁群算法,通过自适应地调整运行过程中的挥发因子来改变路径中信息素浓度,从而有效地克服传统蚁群算法中容易陷入局部最优解和收敛速度慢的现象。
1 基本蚁群算法
1.1蚁群算法原理
人工蚁群算法是受到人们对自然界中真实的蚁群集体行为的研究成果的启发而提的,是一种基于种群的模拟进化算法,属于随机搜索算法。由意大利学者M.Dorigo等人首先提出M.Dorigo等人首次提出该方法时,充分利用了蚁群搜索食物的过程与著名的旅行商问题(TSP)之间的相似性,通过人工模拟蚂蚁搜索食物的过程(通过个体之间的信息交流与相互协作最终找到从蚁穴到食物源的最短路径)来求解TSP。蚁群是如何完成这些复杂的任务的呢?经过人们大量研究发现,蚂蚁个体之间是通过一种称之为外激素(pheromone)的物质进行信息传递从而能相互协作,完成复杂的任务。蚁群之所以表现出复杂有秩序的行为,个体之间的信息交流与相互协作起着重要的作用蚂蚁在运动过程中,能够在它所经过的路径上留下该种物质。
1.2蚁群算法的实现
设将M只蚂蚁放入到N个随机选择的城市,每只蚂蚁每一步的行动是根据一定的依据选择下一个它还没有访问的城市或者一个循环,蚂蚁选择下一个城市的主要依据是:τij(t)(t时刻连接城市i和j的路径上残留信息的浓度),由算法本身提供的信息,ηij(由城市i转移到城市j的起始信息),该起始信息是由要解决的问题给出的.ηij=1/dij为城市i到城市j的先验值,于是,t时刻位于城市i的蚂蚁k选择城市j为目标城市的概率是[2]:式(2.1)

α——残留信息的相对重要程度。
β——期望值的相对重要程度。
为了避免残留信息过多引起的残留信息淹没启发信息的问题,在每个蚂蚁完成对所有n个城市的访问后(即一个循环),必须对残留信息进行更新处理,对旧的信息进行削弱,同时,必须将最新的蚂蚁访问路径的信息加入τi ,j[3],

ρ为残留信息的保留部分,1-ρ为残留信息被削弱的部分,为了防止信息的无限累积,ρ必须小于1。为蚂蚁k在时间段t到(t+n)时间内的访问过程中。在i到j的路径上留下的残留信息浓度。
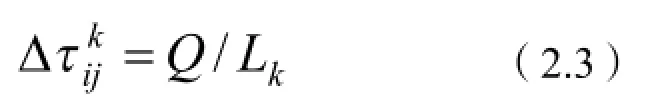
与实际蚁群不同,搜索蚁群算法具有记忆功能,每个蚂蚁个体可以记忆自己所走过的城市.随着时间的推移,以前留下的信息素逐渐消逝,用参数1-ρ表示信息消逝程度,经过n个城市的搜索,蚂蚁完成一次循环,各路径上信息量要作调整:

式中Q----------常数。
2 自适应蚁群算法(Self-Adaptive Ant Colony Algorithm,SAACA)
通过对蚁群算法的分析和研究发现:一般的蚁群算法的选择策略使得进化速度较慢,正反馈原理旨在强化性能较好的解,却容易出现停滞现象。因而提出自适应蚁群算法,从选择策略方面进行修改,采用确定性选择和随机选择相结合的选择策略,在搜索过程中动态地调整作确定性选择的概率当进化到一定代数后,进化方向已经基本确定,这时对路径上信息量作动态凋整。缩小最好和最差路径上的信息量的差距,并且适当加大随机选择的概率,以小于l对解空间的更完全搜索,从而有效地克服基本蚁群算法的不足。
2.1自适应城市选择策略
该算法按照下式3.1确定蚂蚁由所在转移到下一个城市S[5]

其中,S按照公式(2.1),P∈(0,1),r是(0,1)中均匀分布的随机数。当进化方向基本确定后,简单的放大(或缩小)方法调整每一路径上的信息量,该方法不仅能够加快收敛速度,节省搜索时间,而且能够克服停滞行为的过早出现,有利于发现更好的解这对于求解大规模优化问题是有益的。
2.2信息启发因子α和期望启发因子β的自适应调整
当α=0 时,算法就是传统的贪心算法,而当β=0 时,算法就是纯粹的正反馈的启发式算法.刚开始时蚂蚁对链路的情况不了解,链路上的信息素对蚂蚁的寻路影响不大,随着迭代次数的增加,链路上的信息素对蚂蚁的寻路越来越重要,到最后使优胜者链路被选择的概率越来越大,从而优胜者链路的收敛速度越来越快,到最后找到最优路径.所以α,β 值分别按式(3.2)、式(3.3)进行自适应调整:
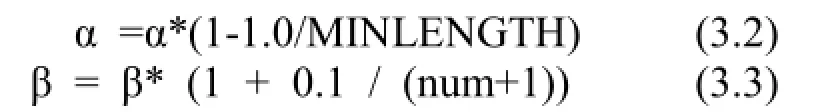
其中 MINLENGTH为当前最佳路径的长度,num为当前运行代数。
2.3路径优化算子
总所周知,在TSP问题中,如果路径中存在交叉路径,则该路径必定不为最优路径。
通过采用2_opt[6]算法能够轻松解决该问题,如图1所示。
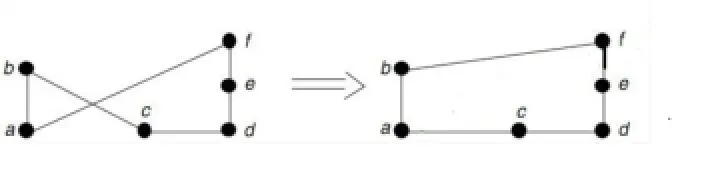
图1 _opt优化算法
通过采用路径优化算子,能使算法拥有更好的收敛能力。
2.4局部收敛时 信息素重新分配
通过判断当前总群最优路径在整个总群的比例来判断算法是否陷入局部收敛。当算法进入局部收敛时,采用新的规则分配各个边上的信息素。信息素的浓度不再是平均分配,而是与路径长度成反比,进而打乱各个边上的信息素浓度,增加搜索能力。
3 仿真实验及分析
3.1实验环境
运行环境为: Visual Studio 2010 采用 C#语言编写程序。
3.2仿真分析
为了检验改进的蚁群算法的求解性能,从通用TSPLIB 算例库中选取多个实例进行测试.在Chc51算例中,参数设置为m=500,Max τ =1;p= 0.6 ,Min τ =0.000001;4;针对Chc51实例SAACA 与IDIA[14]、ACLA[15]算法最优值曲线对比如图2 所示:
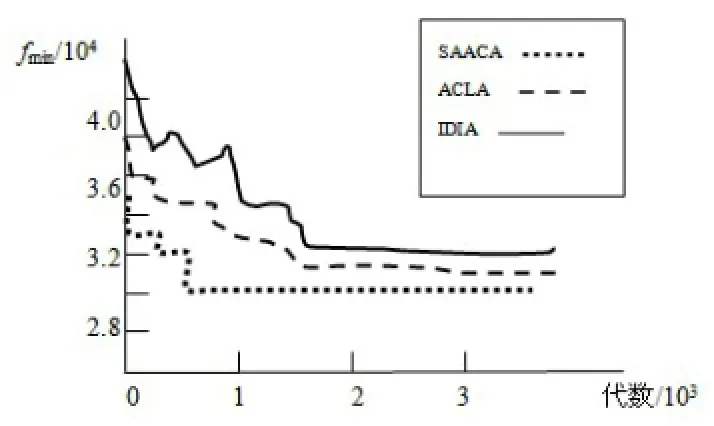
图2 最优值曲线比较
表1是SAACA 与算法ACA[12]、CSA[13]、IDIA[14]和 ACLA[15]算法的一些性能比较,其性能指标包括:MTL(Maximal value of Tour Length)为测试结果中的最长路径值,MITL(Minimal valueof Tour Length)为最短路径值,METL(Mean valueof Tour Length)为路径均值,平均百分误差为:

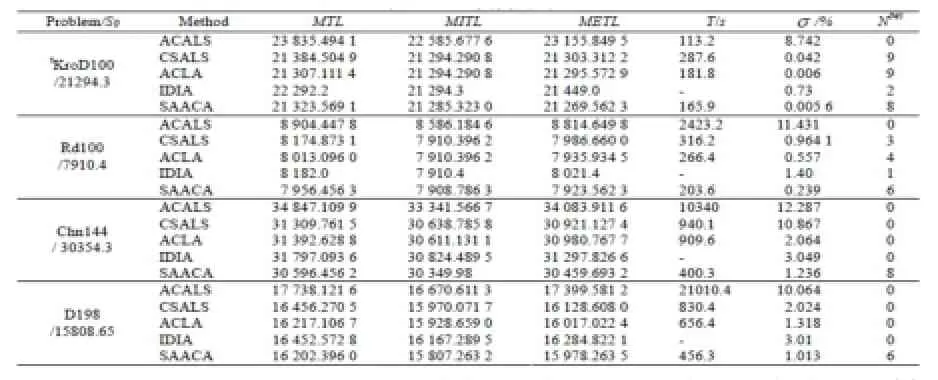
表1 性能比较图
从图1不难发现,本文提出的自适应蚁群算法SAACA运用于TSP问题中,它的最优值都比IDIA[14]、ACLA[15]好,同时收敛速度都比IDIA和ACLA快。从表1可以看出,将SAACA算法运用于四种TSP问题中,除KroD100问题外,其寻优解的最短时间都比ACA[12]、CSA[13]、IDIA[14]和ACLA[15]短。除KroD100问题外,最优解的获得次数都比ACA[12]、CSA[13]、IDIA[14]和ACLA[15]算法多。对于MTL,MITL,METL和平均百分误差等性能指示而言,SAACA都比其他四种算法都好。
3.4结果
改进后的蚁群算法具有比传统蚁群算法和MMAS蚁群算法更强的搜索全局最优解的能力,并具有更好的稳定性和收敛性。对传统蚁群算法容易出现早熟和停滞现象的缺陷,提出了一种动态更新信息素的蚁群算法。实验表明,改进的蚁群算法具有比传统蚁群算法和 MMAS蚁群算法更强的搜索全局最优解的能力,并具有更好的稳定性和收敛性。
4 结束语
蚁群算法发展至今,人们已经针对不同的具体问题提出了许多不同类型的改进蚁群算法模型,但这些改进的蚁群算法模型往往普适性不强,同时基本蚁群算法模型也不能直接应用 于解决所有的优化问题。另外,自然界中的真实蚁群还有许多其他的智能行为,用逆向思维和发散思维开发不同的蚂群算法模型是一条新的发展思路。基于此今后可以从以下几个方面对其模型进行改进:
(1)设计一种通用的蚁群算法普适性模型。
(2)进一步研究自然蚁群行为,提出更加智能化的蚁群混合行为模型。
(3)摆脱传统模型框架,开发新的蚁群算法模型。
因此,关于蚁群算法理论及其应用的研究必将是一个长期的研究课题。相信随着人们对仿生智能系统理论及应用研究的不断深入,蚁群算法这一新兴的仿生优化算法必将展现出更加广阔、更加引人注目的发展前景。
参考文献:
[1]Garey M R,Graham R L,Johnson D S. Some NP -completegeomet ric problems[C]// 8th ACM Symposium on the Theory ofComputing. New York: Association for Computing Machinery,1976: 10-22.
[2]Michal E Z,FOGEL D B. How to solve it: ModernHeuristick[M]. BerlinHeidelberg: Springer2Verlag, 2000.
[3]Stutzl E,Hoos H H. Max-min ant system[J]. Future Generation Computer Systems,2000,16(8): 889-914.
[3]段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社,2006.
[4]焦李成,杜海峰,刘芳,等. 免疫优化计算,学习与识别[M].北京: 科学出版社, 2007.
[5]Kirkpat R S,Gelatt J R,Vecchi M P. Optimization by simulatedannealing[J]. Journal of statistical,1983,34(516): 975-986.
[6]Shi Y,Eberhart C. Particle Swarm Optimization: development,applications and resources[C]//Proc Congress on Evolutionary Computation 2001. Piscataway: IEEE Press, 2001: 81-86.
[7]刘波,刘蒙生. 采用基于模拟退火算法的蚁群算法求解旅行商问题[J]. 华中科技大学学报: 自然科学版,2009(11):26-30.
[8]刘勇,马欣,申志兵. 基于改进蚁群算法的应急救援最优路径选择[J]. 工业安全与环保, 2009(11): 56-57.
[9]张晓玲,黄力. 融入遗传算子的蚁群算法求解TSP问题[J]. 广西民族大学学报: 自然科学版,2009(3): 81-86.
[10]吴建辉,章兢,刘朝华. 基于蚁群算法和免疫算法融合的TSP问题求解[J]. 湖南大学学报: 自然科学版,2009(10):81-87.
[11]峰峰,王仁明,伍佳.求解TSP问题的一种改进蚁群算法[J].自动化技术与应用,2010(7): 1-3.
[12]万晓凤,胡伟,方武义,郑博嘉.基于改进蚁群算法的机器人路径规划研究[J].计算机工程与应用,2014(18):123-125.
[13]刘好斌,胡小兵,赵吉东. 动态调整路径选择的蚁群优化算法[J].计算机工程,2010(17): 201-203.
[14]廖飞雄,马良. 自调节种群的演化算法求解旅行商问题[J].系统仿真学报,2009(9):235-235.
[15]徐金荣,李允,刘海涛,刘攀.一种求解TSP的混合遗传蚁群算法[J].计算机应用,2008(8):223-234.
(责任编辑:廖建勇)
中图分类号:TP301.6
文献标识码:A
doi:10.3969/j.issn.1672-7304.2016.01.061
文章编号:1672–7304(2016)01–0129–04
作者简介:贾丽媛(1972-),女,湖南益阳人,教授,研究方向:算法与人工智能。
Adaptive Ant Colony Algorithm Research and Application in TSP Problems
JIA Li-yuan, ZHOU Cui-hong
(Hunan City University,Yiyang Hunan 413000 )
Abstract:Traditional algorithm in the structure solution process, by the random selection strategy, the selection strategy of making a slow evolution, positive feedback priprinciple aimed at strengthening the performance of a better solution, but prone to stagnation. This is caused by the root causes of the shortcomings of ant colony algorithm. So we from a strategy to modify, we adopt deterministic selection and random selection combining selection strategy, and in the search process dynamically adjust for deterministic choice probability when the evolution to a certain algebra, evolutionary direction has been basically established, then on the amount of information on the path as dynamic full wither. Narrowing the gap between the best and worst path on the amount of information, and appropriate to increase the probability of randomly selected, to less than 1 of the solution space more complete search, which caneffectively overcome the deficiency of the basic ant colony algorithm, this algorithm is adaptive algorithm..
Keywords:Ant colony algorithm; adaptive function; global optimization; function optimization
