基于改进三重训练算法的高光谱图像半监督分类

王立国，杨月霜，刘丹凤

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)



基于改进三重训练算法的高光谱图像半监督分类

王立国，杨月霜，刘丹凤

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

摘要：高光谱数据维数高，有标签的样本数量少，给高光谱图像分类带来困难。本文针对传统三重训练(tri-training)算法在初始有标签样本数量较少的情况下分类器间差异性不足的问题提出了一种基于改进三重训练算法的半监督分类框架。该方法首先通过边缘采样策略(margin Sampling，MS)选取最富含信息量的无标签样本，然后在训练每个分类器之前通过差分进化算法(differential evolution，DE)利用所选取的无标签样本产生新的样本。这些新产生的样本将被标记并且加入训练样本集来帮助初始化分类器。实验结果表明，该方法不仅能够有效地利用无标签样本，而且在有标签数据很少的情况下能够有效地提高分类精度。

关键词：高光谱图像；半监督分类；三重训练；边缘采样；差分进化

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160421.1040.018.html

高光谱遥感技术已经被广泛研究并得到了广泛的应用[1]。高光谱图像高维的数据特点，有限的带标签样本给数据分析和处理带来困难，在分类过程中容易引起Hudges现象[2]。并且带标签的样本获取难度大、代价高，而数据集中存在大量的可利用的无标签样本，这样同时利用有标签数据和无标签数据进行学习的半监督分类方法成为研究的热点[3]。总体来说，半监督分类方法可以分为四类：模型生成算法[4]、半监督支持向量机[5-6]、基于图的半监督算法[7]以及自训练(self-training)、协同训练(co-training)、三重训练(tri-training)等。自训练、协同训练和三重训练属于同一类型，其基本思想是通过分类器的协作对无标签样本进行标记。Co-training要求数据集可以分为两个相互独立的部分，这种对数据集充分性和冗余性的要求在实际情况中是很难满足的[8]。Goldman 等[9]利用不同的学习算法来训练两个独立的分类器，从而使算法的性能不依赖于数据集的划分。三重训练算法对数据集没有特殊的要求，它通过训练三个分类器来实现对无标签样本的标记[10]。文献[11]提出了一种基于co-training的半监督元数据提取方法。文献[12]中，三重训练算法用来改进支持向量机(support vector machine，SVM)。以上提到的算法在许多实际应用中都取得了较好的效果。对于三重训练算法来说，原始有标签样本的缺乏限制着三个分类器之间差异性的提高，从而限制着算法分类精度的提高。为了解决这个问题，许多改进算法都采用差异的机制，例如Bootstrapping方法[13]的应用。但是，如果有标签样本数目非常小，通过这种方法仍不足以得到差异明显的分类器，那么最终的分类性能将与自训练，协同训练类似。Li 等[14]通过在半监督学习过程中引入一定的随机因素来产生差异性。Triguero 等[15]利用最大最小采样和位置调整得到新合成的样本用以丰富原始带标签样本的分布并且给多个分类器引入差异，以提高自标记分类过程的性能。其中，样本的位置调整是通过差分进化算法[16]对样本集合进行寻优而实现的。

本文提出了一种新的基于改进三重训练算法的半监督学习框架。所提算法利用主动学习方法选取富含信息量的无标签样本并且利用差分进化算法产生新的最优样本集。这些新产生的样本将帮助原训练样本初始化三个分类器。通过这种方法，可以丰富训练集样本的分布并且给三重训练算法中三个分类器引入差异因素。

1三重训练算法

三重训练算法是一种常用的半监督分类算法，与协同训练相比，三重训练既不需要两个独立的视图也不需要对监督学习算法有任何限制。它通过从原始标记样本中进行bootstrap采样得到三个有差异的集合训练三个分类器，利用无标签样本集中的样本在训练过程中对其进行更新。在每一个三重训练的循环中，对样本x属于无标签样本集U，如果其他两个分类器对其标记一致，则这个样本被标记且加入到第一个分类器的训练样本中。但是那些有用的无标签样本在下一次循环中要再返回无标签样本集中。以上过程一直循环直到没有分类器再改变为止。最终的结果通过投票法进行决策融合。

如果对某一个无标签样本的预测是正确的，那么分类器将会得到一个新的有效的样本进行再训练，否则分类器将会得到一个噪声样本。按照文献[11]所说，在某种条件下，如果新的被标记的样本足够多，就可以补偿这种噪声的引入。

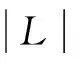
(1)

假设h2与h3分类结果一致的样本个数是z，在这些样本中，二者皆做了正确分类的个数为z′，这样et可以由式(2)估计：

(2)

(3)

(4)

综合以上条件，这些约束条件可以表达为

(5)

根据以上条件的判定，我们就能判断满足何种条件的无标签样本才能够被标记并加入到另一个分类器的训练样本集中。

2改进的三重训练算法

在所提出的改进算法中，首先通过训练SVM分类器并利用边缘采样(MS)策略[18-19]选择信息量丰富的无标签样本，然后利用差分进化(DE)算法在所选无标签样本基础上进行寻优选择。这种方法可以产生新的具有差异性的样本，在三重训练过程中引入差异性。

2.1基于SVM分类器和MS策略的无标签样本集获取

在大量的无标签数据中，并不是所有样本都有助于分类器分类性能的提高。通过主动学习选取最有价值的样本参与运算可以很大程度上降低运算成本[17]。主动学习算法大致可以分为3类：第1类依赖于SVM的特性[18-20]，例如MS策略，第2类是基于分布函数的后验概率估计，第3类是基于评委的方法[21]，例如EQB(query-by-bagging)。本文将利用MS策略从大量的无标签样本中选取信息量丰富的样本参与训练。这种主动学习方法依赖于SVM的几何特性，是一种针对SVM这种具有大分类间隔特点的分类器的样本选择策略，通过计算样本到分类平面的距离，选择距离最近的样本。

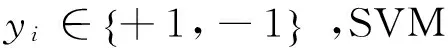
(6)

通过对应的拉格朗日函数及其对偶问题的求解，得到最终的判别函数：

(7)

式中，b*可由Kuhn-Tucher定理推得：

(8)

假设线性分类的情况，支持向量是那些与决策边界距离为1的样本。MS的思想是选择距离分类面最近的那些样本。对于二分类问题，MS策略可以描述为选择符合以下条件的样本：

(9)

对于多分类问题，我们通过“one-against-rest”转化为多个二分类问题。通过训练SVM分类器，可以获得无标签样本集。

2.2基于差分进化(DE)算法的无标签样本寻优

DE算法是基于群体智能理论的优化算法，它通过群体内个体间的合作与竞争来改善种群中候选解的质量。这种优化方法原理简单，操作随机并且有直接的全局搜索，实现起来非常方便。本文利用DE算法在无标签样本集基础上进行寻优操作，产生新的样本加入训练集。其流程可以描述如下：

1)初始化种群。DE利用NP个维数为D的实数值参数向量作为每一代的种群，每个个体表示为

(10)

式中：i表示个体在种群中的序列，G为进化代数。

当前代的第i个种群向量可以描述为

(11)

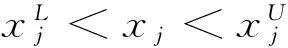
(12)

式中randi,j[0,1]在[0，1]产生的均匀随机数。

2)变异操作。对于每个目标向量Xi,G，i=1,2,…,NP，基本DE算法的变异向量按照如下方式产生：

(13)

3)交叉。为了增加干扰参数向量的多样性，引入交叉操。试验向量变表示为Ui,G=[u1,i,G,u2,i,G,...,uD,i,G]。

(14)

式中：jrand∈[1,2,…,D]为随机整数，Cr为交叉概率。

4)选择。为决定试验向量是否会成为下一代中的成员，DE按照贪婪准则将试验向量与当前种群中的目标向量进行比较。选择过程可以描述为

(15)

图1为本文算法的流程图。

图1　算法流程图Fig.1　Process of the algorithm

实验步骤如下：

1)利用有标签样本训练SVM分类器，记为h0。

2)利用MS策略选择一定量的无标签样本，样本集合记为UM。

3)利用DE算法在集合UM基础上进行寻优操作，得到一定数量的新的样本，并对其进行标记，加入训练样本集。新的训练集记作L′。

4)利用bootstrap采样从L′中得到h1的训练样本集S1，训练SVM分类器得到h1。

5)通过3)和4)得到h2和h3。

6)利用所得分类器开始三重训练过程，对无标签样本进行标记。

3实验部分

3.1实验数据

印第安纳高光谱AVIRIS图像数据是1992年6月摄于美国西北部印第安纳州某农林混合试验场的高光谱图像的一部分。图像大小是144×144，去除20个低信噪比波段以及水汽吸收波段，实际参与处理的图像波段数为200个。选择其中类别数较多的8个主类别参与实验。其地物图如图2(a)。

Pavia工程学院高光谱数据是通过反射光学系统成像光谱仪在帕维亚大学上空获得，去除12个噪声波段后，波段数由115降到103，选取其中144×144大小的图像用来进行实验，其中涵盖8个主要类别。地物图见图2(b)。

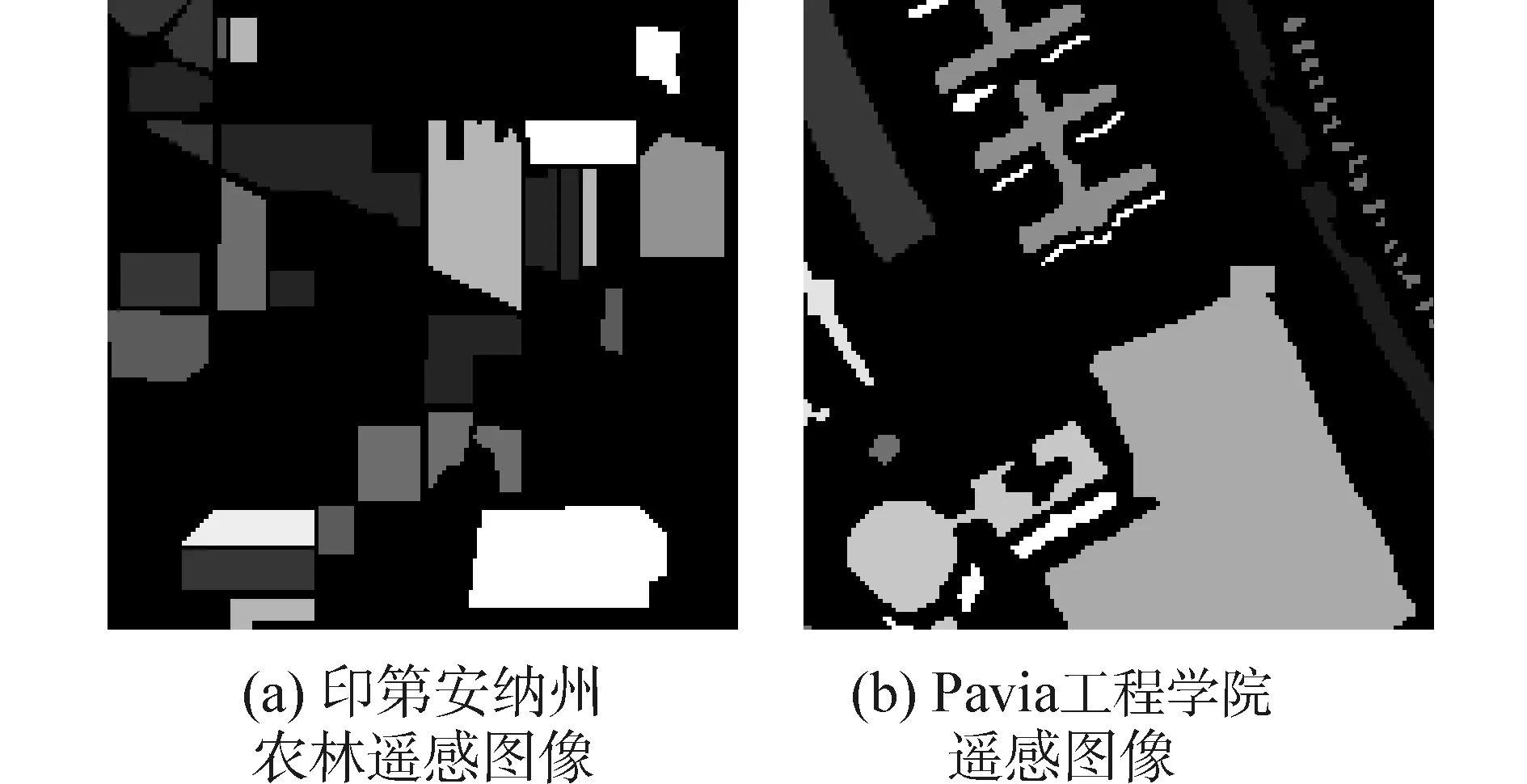
图2　监督信息图Fig.2　Supervised information map

3.2实验设置

本实验的仿真条件：电脑处理器为Intel(R)Core(TM)i3-2350M，4G的RAM，电脑系统为32位windows7操作系统，MATLAB软件为matlab2010a。每次实验进行10次取平均值。

评价准则：每类的分类精度，总体分类精度(overallaccuracy,OA)，平均分类精度(averageaccuracy,AA)，Kappa系数。

为验证本文算法的有效性，在实验中将本文算法与标准SVM，标准Tri-training进行比较。

在实验中，所选无标签样本数为20，差分进化算法的参数为NP=20,F=0.8,Cr=0.8。tri-training算法采用标准SVM作为基分类器。SVM采用径向基核函数， “one-against-rest”多分类方法。惩罚因子C以及核参数σ通过网格搜索法在集合[10，103] 和 [10-2，102]中取得最优值。

3.3印第安纳高光谱AVIRIS图像实验

实验中每类随机选取10%作为训练样本，剩余的为测试样本。在训练样本中选取10个作为有标签数据，余下的作为无标签数据。

表1给出了SVM,标准tri-training,改进tri-training算法的分类结果，其中给出平均分类精度(AA)，总体分类精度(OA)以及Kappa系数。由表1可知，标准tri-training算法的分类性能与SVM相比有了明显的提高。其中，AA提高了1.45%，OA提高了2.73%，Kappa系数提高了0.030 5。这是由于半监督分类方法能够有效的利用大量的无标签样本所包含的信息，使分类结果更加准确。对于改进的tri-training算法，其AA比标准tri-training算法提高了1.05%，OA提高了0.52%，Kappa提高了0.007 1。通过MS算法与DE算法的结合，产生了新的样本用以丰富训练集合，并且给tri-training算法的3个分类器增加了差异性从而导致分类性能的提升。

相应的分类灰度图见图3所示。由图3可以看出，图3(c)中错分的样本点明显少于图3(a)和(b)。

表1印第安纳高光谱图像分类结果

Table 1Classification results for the AVIRIS data of Indian Pine

评价准则SVM标准tri-training改进tri-trainingAA78.6280.8381.88OA74.5478.6279.14Kappa0.69950.74590.7530

图3　三种方法的分类结果图Fig.3　Classification maps for the AVIRIS data of Indian Pine

为了更清楚的看出本文所提算法的优越性，图4(a)展示了3种算法分类结果的柱状图。由图可知，改进的tri-training算法能够有效提高分类精度。

3.4Pavia工程学院高光谱图像实验

实验中每类随机选取10%作为训练样本，剩余的为测试样本。在训练样本中选取10个作为有标签数据，余下的作为无标签数据。评价准则选取平均分类精度(AA),总体分类精度(OA)和Kappa系数。表2列出了SVM,标准tri-training,改进tri-training算法的实验仿真结果。由表2可知，tri-training算法的AA比SVM提高了0.61%，OA提高了1.21%，Kappa提高了0.0136。而本文所提出的改进算法比标准tri-training算法的分类结果有进一步的提高，AA 、OA 和Kappa 的提高值分别为1.83%，2.83%和0.043。由此可知本文所提算法通过丰富训练样本的分布同时给tri-training算法的3个分类器增加差异性，使其分类性能有了明显的提高。图5给出了3种算法的分类灰度图。图4(b)以柱状图的形式使我们能够清晰看出本文所提算法的优势。

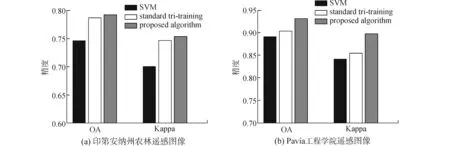
图4　不同算法的分类结果比较Fig.4　Classification results comparison of different algorithms

Table 2Classification results for the data of University of Pavia

评价准则SVM标准tri-training改进tri-trainingAA90.7991.4093.23OA88.9790.1893.01Kappa0.83980.85340.8964

图5　Pavia工程学院的分类结果图 Fig.5　Classification maps for the data of University of Pavia

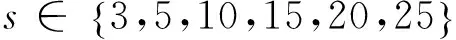
图6　带标签样本数s与OA的关系曲线 Fig.6　Influence of s on the overall accuracy (OA) for the AVIRIS data of Indian Pine

图7描述了初始带标签样本数s与总体分类精度OA的关系曲线，观察曲线我们可以得知分类精度在一定范围内随着初始带标签样本数的增加而增大，这是由于带标签样本携带着更多的监督信息，能够促进分类性能的提升。在s=3时，本文所提算法的OA比标准tri-training方法提高了3.87%，随着s的增加，这种差距总体上是缩小的，在s=25 时变为1.4%。这进一步验证了本文所提算法在初始带标签样本数目较少的情况下具有很大的优势。

图7　Pavia工程学院的带标签样本数s与OA的关系曲线Fig.7　Influence of s on the overall accuracy (OA) for the data of University of Pavia

4结论

本文利用MS策略和DE算法对三重训练算法进行了改进，提出了一种新的半监督分类框架。通过MS策略选取最富含信息量的无标签样本，并在这些样本的基础上利用DE算法产生新的样本用来丰富初始的训练样本集，同时通过这种方法给三重训练算法的三个分类器引入差异因素。与标准三重训练算法的对比实验结果表明，所提算法具有两方面的特征：

1)分类精度和Kappa系数都有明显提高；

2)分类优势在初始有标签样本数目较少的情况下更加明显。

在以后的工作中，可以继续研究充分利用无标签样本的方法，并且探究如何进一步增加三重训练方法中3个基分类的差异性。

参考文献：

[1]WANG Liguo, JIA Xiuping. Integration of soft and hard classifications using extended support vector machines[J]. IEEE geoscience and remote sensing letters, 2009, 6(3): 543-547.

[2]SHAHSHAHANI B M, LANDGREBE D A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the hughes phenomenon[J]. IEEE transactions on geoscience and remote sensing, 1994, 32(5): 1087-1095.

[3]ZHU Xiaojin. Semi-supervised learning literature survey[D]. Madison: University of Wisconsin-Madison, 2008.

[4]BARALDI A, BRUZZONE L, BLONDA P. A multiscale expectation maximization semisupervised classifier suitable for badly posed image classification[J]. IEEE transactions on image processing, 2006, 15(8): 2208-2225.

[5]JOACHIMS T. Transductive inference for text classification using support vector machines[C]//Proceedings of the 16th International Conference on Machine Learning. Bled, Slovenia, 1999: 200-209.

[6]CHI Mingmin, BRUZZONE L. Classification of hyperspectral data by continuation semi-supervised SVM[C]//Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium. Barcelona, 2007: 3794-3797.

[7]BLUM A, CHAWLA S. Learning from labeled and unlabeled data using graph mincuts[C]//Proceedings of the 18th International Conference on Machine Learning. Williamston, 2001: 19-26.

[8]BLUM A, MITCHELL T. Combining labeled and unlabeled data with co-training[C]//Proceedings of the 11th Annual Conference on Computational Learning Theory. Madison, 1998: 92-100.

[9]GOLDMAN S, ZHOU Yan. Enhancing supervised learning with unlabeled data[C]//Proceedings of the 17th international conference on machine learning. San Francisco, CA, 2000: 327-334.

[10]ZHOU Zhihua, LI Ming. Tri-training: Exploiting unlabeled data using three classifiers[J]. IEEE transactions on knowledge and data engineering, 2005, 17(11): 1529-1541.

[11]ZHANG Youmin, YU Zhengtao, LIU Li, et al. Semi-supervised expert metadata extraction based on co-training style[C]//Proceedings of the 9th international conference on fuzzy systems and knowledge discovery. Chongqing, 2012: 1344-1347.

[12]LI Kunlun, ZHANG Wei, MA Xiaotao, et al. A novel semisupervised svm based on tri-training[C]//Proceedings of the 2nd International Symposium on Intelligent Information Technology Application. Shanghai, China, 2008: 47-51.

[13]BREIMAN L. Bagging predictors[J]. Machine learning, 1996, 24(2): 123-140.

[14]LI Ming, ZHOU Zhihua. Improve computer-aided diagnosis with machine learning techniques using undiagnosed samples[J]. IEEE transactions on systems, man, and cybernetics, part A: systems and humans, 2007, 37(6): 1088-1098.

[15]TRIGUERO I, GARCIA S, HERRERA F. SEG-SSC: a framework based on synthetic examples generation for self-labeled semi-supervised classification[J]. IEEE transactions on cybernetics, 2015, 45(4): 622-634.

[16]PRICE K V, STORN R M, LAMPINEN J A. Differential evolution: a practical approach to global optimization[M]. Berlin Heidelberg: Springer, 2005: 292.

[17]MACKAY D J C. Information-based objective functions for active data selection[J]. Neural computation, 1992, 4(4): 590-604.

[18]SCHOHN G, COHN D. Less is more: Active learning with support vectors machines[C]//Proceedings of the 17th international conference on machine learning. Stanford, CA, 2000: 839-846.

[19]CAMPBELL C, CRISTIANINI N, SMOLA A. Query learning with large margin classifiers[C]//Proceedings of the 17th international conference on machine learning. Stanford, CA, 2000: 111-118.

[20]NGUYEN H T, SMEULDERS A. Active learning using pre-clustering[C]/Proceedings of the 21th international conference on machine learning. Banff, AB, Canada, 2004: 79.

[21]FREUND Y, SEUNG H, SHAMIR E, et al. Selective sampling using the query by committee algorithm[J]. Machine learning, 1997, 28(2/3): 133-168.

本文引用格式：

王立国，杨月霜，刘丹凤. 基于改进三重训练算法的高光谱图像半监督分类[J]. 哈尔滨工程大学学报， 2016, 37(6): 849-854.

WANG Liguo， YANG Yueshuang， LIU Danfeng. Semi-supervised classification for hyperspectral image based on improved tri-training method[J]. Journal of Harbin Engineering University, 2016, 37(6): 849-854.

收稿日期：2015-05-27.

基金项目：国家自然科学基金项目(60802059)；教育部博士点新教师基金项目(200802171003)；黑龙江省自然科学基金项目(F201409).

作者简介：王立国(1974-)，男，教授，博士生导师.

通信作者：王立国，wangliguo@hrbeu.edu.cn.

DOI:10.11990/jheu.201505078

中图分类号：TP75

文献标志码：A

文章编号：1006-7043(2016)06-0849-06

Semi-supervised classification for hyperspectral image based on improved tri-training method

WANG Liguo， YANG Yueshuang， LIU Danfeng

(College of Information and Communications Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract：The classification of hyperspectral images is difficult due to their highly dimensional features and limited number of training samples. Tri-training learning is a widely used semi-supervised classification method that addresses the problem of the deficiency of labeled examples. In this paper, we propose a novel semi-supervised learning algorithm based on an improved tri-training method. The proposed algorithm first uses a margin sampling (MS) technique to select the most informative samples, and then uses a differential evolution (DE) algorithm to generate new samples within the selected unlabeled samples. The newly generated samples are then labeled and added to the training set to help initialize the classifiers. We experimentally validated the proposed method using real hyperspectral data sets, and the results indicate that the proposed method can significantly reduce the need for labeled samples and can achieve high accuracy compared with state-of-the-art algorithms.

Keywords：hyperspectral image; semi-supervised classification; tri-training; margin sampling； differential evolution

网络出版日期：2016-04-21.