还科学探索以本来面目

杭雅琴

【摘要】教师要在课堂上让学生经历数学知识的形成过程，通过观察、猜想、验证、比较等活动，探索出规律，从而获得一定的数学思想方法，积累一定的数学活动经验，进而提升学生的数学思维水平。

【关键词】探索规律活动经验猜想验证

《钉子板上的多边形》是五年级上册综合实践这一领域的内容，是一节探索规律的课。这节课的价值不仅仅在于得出一个结论，而是重在让学生经历规律探索的一般过程与方法，积累数学活动经验，培养学生善于发现的眼光，科学严谨的态度和归纳概括的能力。

因此，我想通过本节课的教学，除了达成知识目标——找到规律外，还旨在通过以下四个“环节”，突出找的过程和方法，还科学探索以本来面目。

一、 扶

在老师指导下的自主探究活动，引导学生发现多边形内有1枚、2枚钉子的多边形的面积与边上钉子数之间的关系。

出示以下4个图形。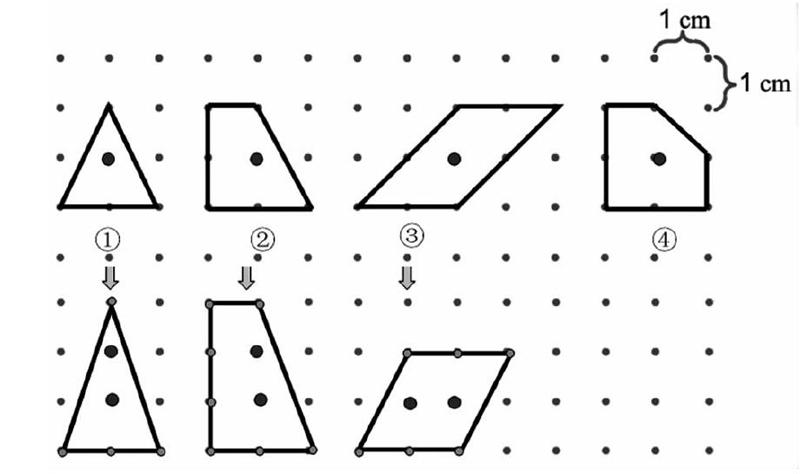

（1） 数一数，上面每个多边形的边上有几枚钉子？面积分别是多少？

（2） 仔细观察表中的数据，你有什么发现？

（3） 图形的面积一般用什么字母表示？（s）在这里我们用n来表示多边形边上的钉子数。这样，你会用字母式来表示多边形边上的钉子数与面积之间的关系吗？（得出S=n÷2）

S=n÷2告诉我们，只要知道了n，就能求出S，是吗？下面我们就用这个结论来解决一些问题。

（1） 把原来的三角形拉长（如图）。

学生数出n=4，代入公式算出S=2，此时许多学生会发现矛盾，面积明明变大了，怎么还是2呢？计算实际面积得到大三角形的面积是3。

（2） 继续把后面两个多边形也做同样的处理，让学生数一数、算一算、比一比，发现结果也不符。

（3） 为什么不符合刚才的规律呢？引导学生仔细观察变化前后的多边形，你有什么发现？（上面多边形内的钉子数是1，下面是2）

（4） 看来多边形内的钉子数也和我们刚才的研究有关。如果用字母a表示多边形内的钉子数，那么在a等于几的情况下，S=n÷2成立？

（5） 那是不是所有的形内只有一枚钉子的多边形都符合这一条规律呢？你们觉得自己还应该做些什么？（拿出一号研究单举例验证：画一画、填一填、想一想、议一议。）

刚才我们通过研究发现，当a=1时，钉子板上多边形的面积正好是边上钉子数的一半，那么当a=2时，多边形边上的钉子数和面积又有怎样的关系呢？

（1） 直接观察刚才变化后的三幅图，议一议，说一说。

（2） 是不是所有形内有两钉子的多边形都符合这条规律呢？拿出二号研究单，举例验证。

对于A=2的图例，我没有重起炉灶，而是在原来多边形的基础上做延伸处理，其用意是为了便于比较，及时聚集问题本质。

二、 放

大胆猜想的自主探究活动，学生独立研究多边形内有3枚、4枚钉子的多边形的面积与边上钉子数之间的关系。

由a=2，你想到了什么？（a=3，S=n÷2+2；a=4，S=n÷2+3……）

是这样吗？这些仅仅是我们的猜想，要知道对不对还得举例验证。下面我们分分工，第一二组举例验证a=3的情况，第三四组举例验证a=4的情况，拿出三号研究单开展研究。

如果a=5呢？a=80呢？

观察这些关系式，你发现了什么？（后面的加数都比前面的a少1.）那你们是怎么看a=1，S=n÷2的呢？

这一环节让学生在猜想中模仿，在模仿中应用，有应用中认知，不断推进和深化学习过程。

三、 留

a=0时，多边形的面积和它边上的钉子数是不是也有这样的关系，留个尾巴给学生课后去研究。

那如果a=0时呢？还符合这个规律吗？老师可以非常肯定地告诉大家，符合！a=0的情况留给同学们课后用四号研究单去研究吧。

新的问题的产生不管是学生想到的，还是老师给出的，都将会引导着学生一直研究、学习下去，把“课外”也变成“课堂”。

四、 理

引导学生回顾、整理、归纳出一般规律，师生共同完善知识的整体建构。

同学们，要想让自己变聪明，首先我们要学会由一个点想到许多个点，例如刚才我们由a=1想到了a=2、a=3……

我们还要学会把许多的点变成一个点。例如你有没有想到把a=1时，S=n÷2；a=2，S=n÷2+1……这么多条规律再合并成一条规律呢？学生讨论。（得出：S=n÷2+a-1）

著名的数学家开普勒就说过这样一句名言：数学就是研究千变万化中不变的规律。而今天这节课我们探索并发现的这条规律正是数学上著名的皮克定理。（简单介绍）

学生在老师的引导下，通过观察、讨论、整理探究成果、回顾学习过程，对获得的知识进行总结与梳理，提升学生的数学思维水平。