随机生长四参数生成孔隙模型及其分形描述
2016-07-27朱维伟姚约东王德强
朱维伟 姚约东 邹 威 王德强
中国石油大学(北京)石油工程教育部重点实验室, 北京 昌平 102249
随机生长四参数生成孔隙模型及其分形描述
朱维伟姚约东邹威王德强
中国石油大学(北京)石油工程教育部重点实验室,北京昌平102249
摘要:储层孔隙是油气储存和运移的主要通道,孔隙结构的研究在油气田开发中占有十分重要的位置。通过随机生长四参数算法,建立了21组不同孔隙度、相同概率生长方向和若干组相同孔隙度、具有优势生长方向的孔隙模型,定量计算了各个孔隙模型的分形盒维数及其多重分形谱,对比研究孔隙结构与分形维数相关关系的结果表明孔隙介质具有很好的分形性质,孔隙度与盒维数在双对数表示下,具有高度线性相关性。多重分形谱特征参数�Δα与孔隙度相对独立,能够反映孔隙结构的非均质性,其值越大,说明孔隙结构的非均质性越强。
关键词:随机生长四参数;孔隙度;分形;盒维数;多重分形
0前言
孔隙微观结构的研究对石油与天然气开发有重要意义。常规的孔隙结构研究主要有毛管压力曲线法,核磁共振法,扫描电镜法,CT扫描法和测井方法等[1-3],这些实验或者现场测试方法一般耗时长,费用高,过程复杂。本文采用随机生长四参数法建立孔隙模型,具有操作简单、结果直观、后续计算方便的优势。储层孔隙被认为是具有统计意义上的分形体,但通常是基于理论推导,或二维图像的计算,缺少三维储层的分形计算。对于孔隙结构与分形参数的相关关系,也讨论甚少,对于局部孔隙结构的表征,也是常规分形所不能表达的。本文基于单重和多重分形盒维数的计算方法,深入研究了孔隙结构和分形维数的相关关系,并且利用多重分形进行孔隙结构非均质性的表征。
1随机生长四参数法建立孔隙模型
本文采用随机生长四参数算法[4-5],进行随机孔隙结构建模,建立由孔隙和固体颗粒两相构成的三维多孔介质模型,其中孔隙为生长相,固体颗粒为非生长相,初始相全为固体颗粒。具体构造步骤如下:
1)本文构建立方体区域作为孔隙模型的生长区域。在构造区域内随机分布孔隙节点生长核,其分布概率为pd,对于构造区域内每一个网格节点在[0,1]区间内生成平均分布随机数,随机数不大于pd的节点即为生长核。
2)对于初始随机分布的孔隙节点进行遍历,将每个孔隙节点向三维空间进行随机生长。其生长方向涉及到26个方向,包括6个主方向,12个面对角方向,8个体对角方向。本文算法是对初始孔隙节点和生长之后的孔隙节点循环遍历,不涉及到单独节点连续生长的情况,因此为了生成各个方向生长均匀的孔隙模型,各个方向的生长概率ps均相同,以孔隙节点为生长原点,向26个方向上的非孔隙邻点重新生成随机数,当生成的随机数小于ps时,该点生长为孔隙节点。
按照上述算法,得到的多孔介质模型见图1。
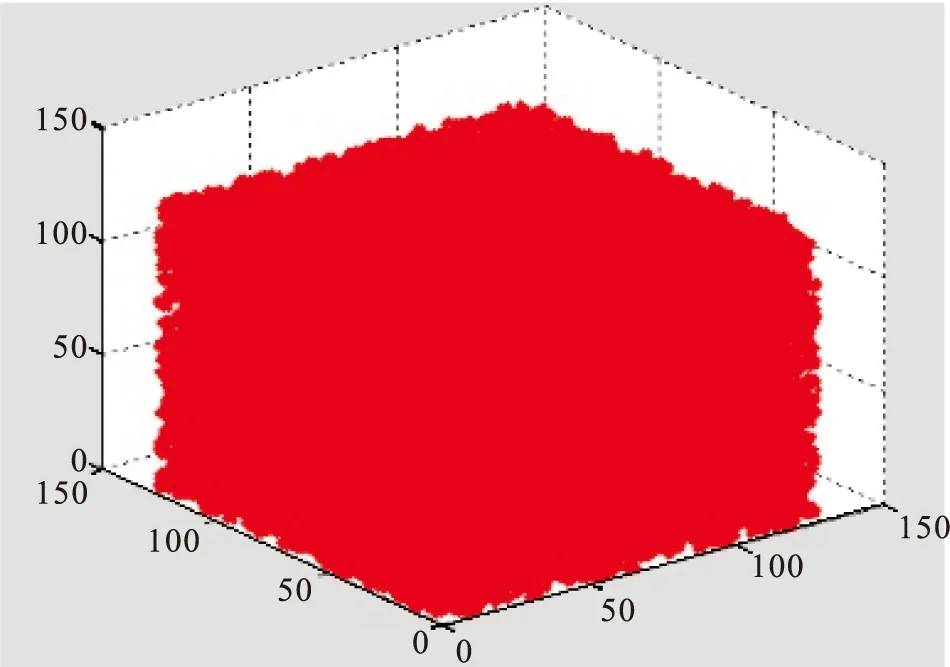
图1 孔隙度为0.15的多孔介质模型
2.1孔隙结构及其分形维数
Mandelbrot提出的分形概念[6]已经广泛运用于多学科的理论研究和工程应用[7-12]。分形体的根本性质是自相似性,指局部和整体有某种相似的形,包括严格自相似和统计意义上的自相似两种情况。长期以来,储层孔隙被认为是具有统计意义上的分形体[13-17],本文通过具体的三维孔隙结构计算其分形维数进行验证,并且进一步探讨孔隙度和分形维数的内在关联。
分形维数的定义中,由于盒计数维数求取方便,含义简明直观,容易理解,因此有较为广泛的运用,在描述孔隙分形中,也通常采用盒计数维数进行表征[18],其求取公式如下:
(1)
根据式(1)计算21组不同孔隙度模型相应的盒维数,结果表明随机孔隙模型具有自相似性,各模型相关系数均高达0.99以上,不同孔隙度下的盒维数D相关关系曲线如图2。
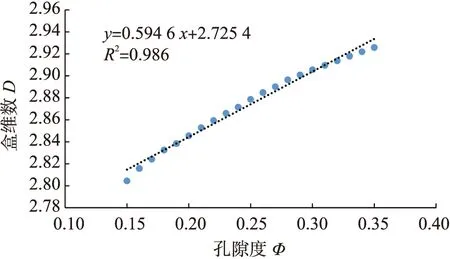
图2 孔隙度与盒维数相关曲线
从图2可以看出,随着孔隙度的增加,孔隙模型的分形维数也随之增大,其增长模式接近线形,拟合程度达到0.986,进一步做出孔隙度对数值和分形维数对数值的相关曲线(图3)。
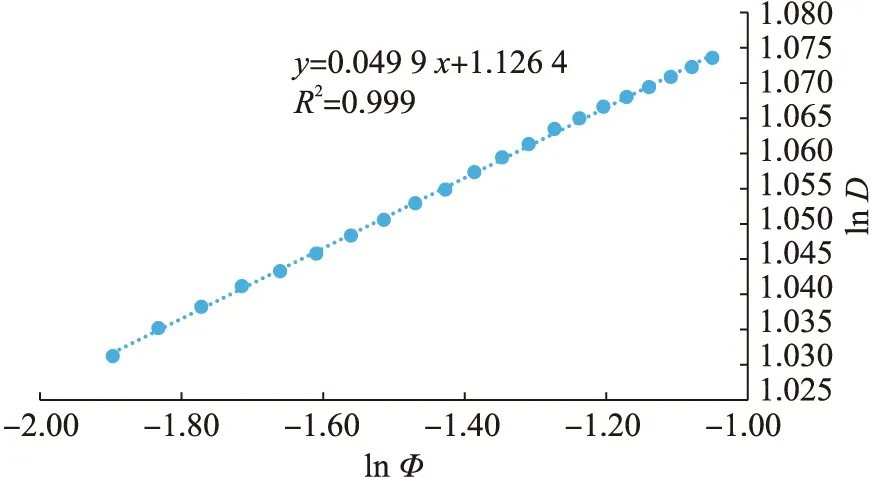
图3 孔隙度与盒维数双对数相关曲线
由图3拟合结果可以看出,孔隙度和盒维数的双对数值成高度的线性相关性,相关系数达到0.999,因此储层孔隙分形维数对数值可以严格表征储层的孔隙度大小。
2.2孔隙结构的多重分形描述
孔隙结构的盒维数只能反映出储层孔隙分布的大致情况,不能对孔隙分布的局部信息进行表达,因此引入多重分形对孔隙分布的局部信息进行描述[19-20]。
多重分形指一个分形集由若干个子集组成,不同的标度情况下,各个子集的分形维数也不同。多重分形的盒维数计数方法就是在考虑盒子内像素数的差别,归一化后得到一个概率分布集,再用一个多重分形谱进行描述。对于孔隙结构的多重分形描述,其关键点在于定义孔隙系统的概率分布函数如式(2):
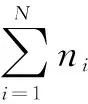
(2)
χq(r)=∑Pi(r)q=r(q)
(3)
由式(4)、(5)得到多重分形谱线:
(4)
(5)
2.3多重分形谱的求取
以孔隙度分别为0.15,0.25四组孔隙模型为例,绘制lnχq(r)-ln r曲线(图4)。
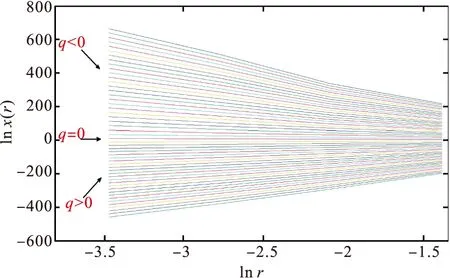
a)孔隙度=0.15
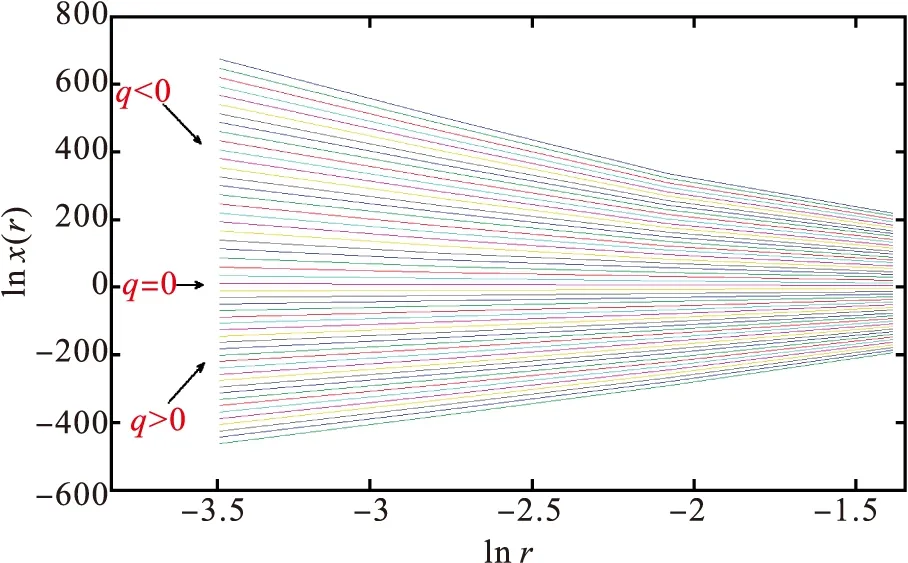
b)孔隙度=0.25图4 不同孔隙度模型lnχq(r)-ln r曲线
从图4可以发现,lnχq(r)和ln r成很好的线性关系,说明所建立的孔隙模型满足分形标度不变性质,是多重分形体,可以求解其多重分形谱。出于计算稳定性的要求,本文在尺度r=1/32下,计算各个孔隙模型的多重分形谱线,见图5。
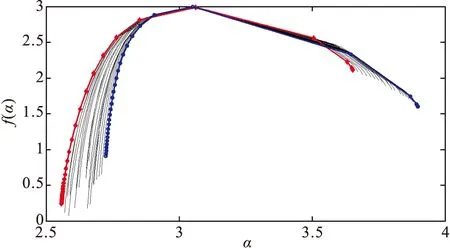
图5 不同孔隙度多重分形谱线
图5中红色曲线为孔隙度为0.15的多重分形谱线,蓝色曲线为孔隙度为0.35的多重分形谱线,可以看出孔隙度从0.15至0.35的所有模型多重分形谱线都在由红蓝线构成的包络线中,因此,不同孔隙度模型的多重分形谱线具有相似性。以包络线为代表进行具体分析,见表1。
表1不同孔隙度模型的多重分形参数比较
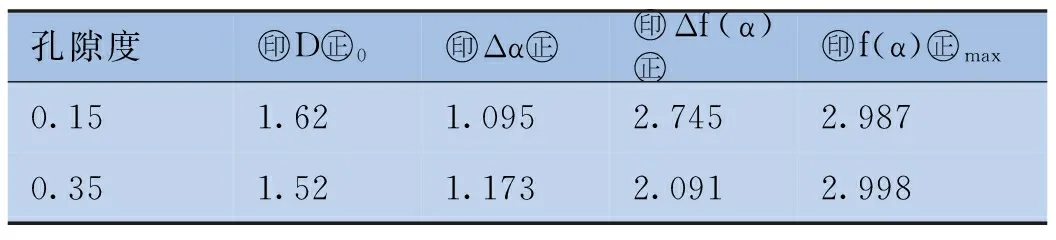
孔隙度㊞D㊣0㊞Δα㊣㊞Δf(α)㊣㊞f(α)㊣max0.151.621.0952.7452.9870.351.521.1732.0912.998
2.4非均质孔隙及其分形描述
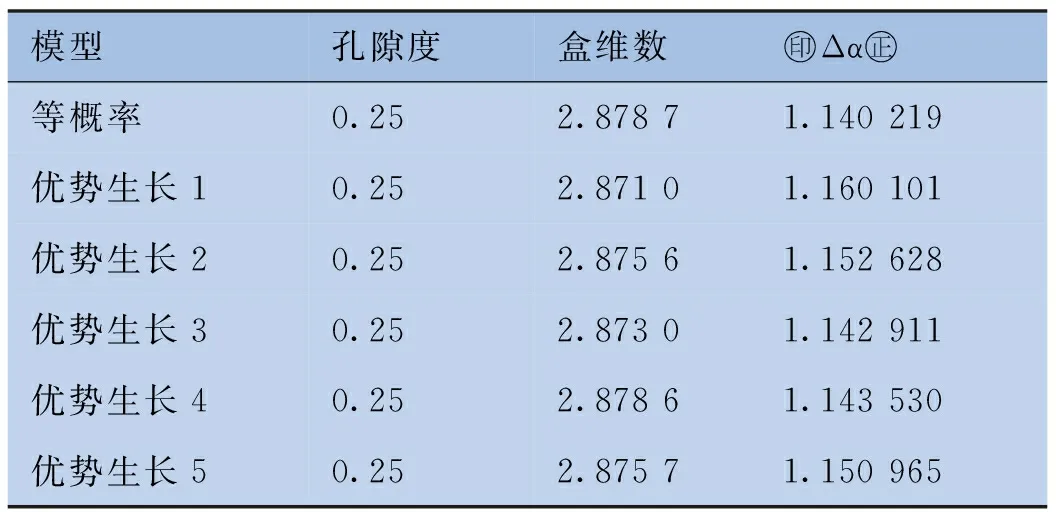
由于天然沉积、地质构造等作用,天然的储层孔隙结构显然与本文所建立的随机孔隙结构有明显不同,孔隙的生长在各个方向并不是等概率生长,本文建立了孔隙度为0.25,存在优势生长方向的非均质孔隙模型。通过提高优势生长方向的生长概率来实现优势生长,其优势方向,沿某一方向或沿某一平面生长,共建立非均质模型5个,与等概率随机生长模型对比,结果见表2。
表2存在优势生长方向的随机孔隙模型分形参数对比
模型孔隙度盒维数㊞Δα㊣等概率0.252.87871.140219优势生长10.252.87101.160101优势生长20.252.87561.152628优势生长30.252.87301.142911优势生长40.252.87861.143530优势生长50.252.87571.150965
从表2可以看出,存在优势方向的非均质孔隙结构,其盒维数均小于等概率生长的随机孔隙模型,这是由于存在优势方向,即孔隙生长会更有向优势方向生长的趋势,从而减弱了整体占满整个构造空间的趋势,因此盒维数会有所有下降。由于盒维数与孔隙度有很强的相关性,因此盒维数并不能独立反映出孔隙结构的非均质性,然而Δα的值相对于孔隙度是独立的,能够独立反映出孔隙结构的非均质性,从表2可以看出,非均质的孔隙结构的Δα值更大。
3结论
1)孔隙结构是分形体,能够用分形理论进行研究,孔隙结构的分形维数与孔隙度成较好的线性关系,在双对数坐标下,两者有相当高的线性相关性,相关系数达到0.999以上。
2)分形盒维数与孔隙度关联性大,但只能反映孔隙结构的总体状况,不能反映局部分布结构和非均质性。
3)孔隙结构具备多重分形的标度不变性质,是多重分形体,其特征参数Δα与孔隙度相互独立,能够有效描述孔隙结构的局部信息和非均质性,其值越大,则表示孔隙结构非均质性越强。
参考文献:
[1] 郝乐伟,王琪,唐俊.储层岩石微观孔隙结构研究方法与理论综述[J].岩性油气藏,2013,25(5):123-128.
Hao Lewei, Wang Qi, Tang Jun. Research Progress of Reservoir Microscopic Pore Structure [J]. Lithologic Reservoirs, 2013, 25 (5): 123-128.
[2] 赖锦,王贵文,陈敏,等.基于岩石物理相的储集层孔隙结构分类评价—以鄂尔多斯盆地姬塬地区长8油层组为例[J].石油勘探与开发,2013,40(5):566-572.
Lai Jin, Wang Guiwen, Chen Min, et al. Pore Structures Evaluation of Low Permeability Clastic Reservoirs Based on Petrophysical Facies: A Case Study on Chang 8 Reservoir in Jiyuan Region, Ordos Basin [J]. Petroleum Exploration and Development, 2013, 40 (5): 566-572.
[3] 李海燕,岳大力,张秀娟.苏里格气田低渗透储层微观孔隙结构特征及其分类评价方法[J].地学前缘,2012,19(2):133-139.
Li Haiyan, Yue Dali, Zhang Xiujuan. Characteristics of Pore Structure and Reservoir Evaluation of Low Permeability Reservoir in Sulige Gas Field [J]. Science Frontiers, 2012, 19 (2): 133-139.
[4] 李仁民,刘松玉,方磊,等.采用随机生长四参数生成法构造黏土微观结构[J].浙江大学学报:(工学版),2010,10(10):1897-1901.
Li Renmin, Liu Songyu, Fang Lei, et al. Micro-Structure of Clay Generated by Quartet Structure Generation Set [J]. Journal of Zhejiang University (Engineering Science), 2010, 10 (10): 1897-1901.
[5] Wang M, Pan N. Numerical Analyses of Effective Dielectric Constant of Multiphase Microporous Media [J]. Journal of Applied Physics, 2007, 101 (11): 114102.
[6] 孙霞,吴自勤.分形原理及应用[M].合肥:中国科学技术大学出版社,2003:53-74.
Sun Xia, Wu Ziqing. The Principle and Application of Fractal [M]. Hefei: University of Science and Technology of China Press, 2003: 53-74.
[7] 李云开,杨培岭,任树梅,等.土壤水分与溶质运移机制的分形理论研究进展[J].水科学进展,2005,16(6):892-899
Li Yunkai, Yang Peiling, Ren Shumei, et al. Development in Research on the Fractal Theory of Soil Water and Solute Transportation Mechanisms [J]. Advance in Water Science, 2005, 16 (6): 892-899
[8] 王国梁,周生路,赵其国.土壤颗粒的体积分形维数及其在土地利用中的应用[J].土壤学报,2005,42(4):545-550
Wang Guoliang, Zhou Shenglu, Zhao Qiguo. Volume Fractal Dimension of Soil Particles and Its Applications to Land Use [J]. Acta Pedologica Sinica, 2005, 42 (4): 545-550
[9] 刘勇军,朱岳明,丰土根,等.随机土体结构模型理论及应用[J].岩土工程学报,2001,23(3):354-357.Liu Yongjun, Zhu Yueming, Feng Tugen, et al. Study on Random Soil Frame Model and Its Application [J]. Chinese Journal of Geotechnical Engineering, 2001, 23 (3): 354-357.
[10] 王唯威.分形多孔介质内导热与流动数值模拟研究[D].北京:中国科学院工程热物理研究所,2006.
Wang Weiwei. Numerical Study of Heat Conduction in Fractal Porous Media [D]. Beijing: Institute of Engineering Thermophysics, CAS, 2006.
[11] 杨培岭,罗远培,石元春.用粒径的重量分布表征的土壤分形特征[J].科学通报,1993,38(20):1896-1899.
Yang Peiling, Luo Yuanpei, Shi Yuanchun. Soil Fractal Characteristics Measured by Mass of Particle-Size Distribution [J]. Chinese Science Bulletin, 1993, 38 (20): 1896-1899.
[12] 黄冠华,詹卫华.土壤颗粒的分形特征及其应用[J].土壤学报,2002,39(4):490-497.
Huang Guanhua, Zhan Weihua. Fractal Property of Soil Particle Size Distribution and Its Application [J]. Acta Pedologica Sinica, 2002, 39 (4): 490-497.
[13] 马新仿,张士诚,郎兆新.储层岩石孔隙结构的分形研究[J].中国矿业,2003,12(9):46-48.
Ma Xinfang, Zhang Shicheng, Lang Zhaoxin. Fractal Research on Pore Structure in Reservoir Rock [J]. China Mining Magazine, 2003, 12 (9): 46-48.
[14] 张宪国,张涛,林承焰.基于孔隙分形特征的低渗透储层孔隙结构评价[J].岩性油气藏2013,25(6):40-45.
Zhang Xianguo, Zhang Tao, Lin Chengyan. Pore Structure Evaluation of Low Permeability Reservoir Based on Pore Fractal Features [J]. Lithologic Reservoirs, 2013, 25 (6): 40-45.
[15] 贾芬淑,沈平平,李克文.砂岩孔隙结构的分形特征及应用研究[J].断块油气田,1995,2(1):16-21.Jia Fenshu, Shen Pingping, Li Kewen. Study on the Fracture Characteristics of Sandstone Pore Structure and Its Application [J]. Fault-Block Oil & Gas Field, 1995, 2 (1): 16-21.
[16] 杨建,陈家军,杨周喜,等.松散砂粒孔隙结构、孔隙分形特征及渗透率研究[J].水文地质工程地质,2008,35(3):93-96.
Yang Jian, Chen Jiajun, Yang Zhouxi et al. A Study of Pore Structure, Pore Fractal Feature and Permeability of Unconsolidated Sand [J]. Hydrogeology and Engineering Geology, 2008, 35 (3): 93-96.
[17] 张东晖,杨浩,施明恒.多孔介质分形模型的难点与探索[J].东南大学学报,2002,32(5):692-697.
Zhang Donghui, Yang Hao, Shi Mingheng.Important Prob
lems of Fractal Model in Porous Media [J]. Journal ofSoutheast University, 2002, 32 (5): 692-697.
[18] 彭瑞东,谢和平,鞠杨.二维数字图像分形维数的计算方法[J].中国矿业大学学报,2004,33(1):19-24.
Peng Ruidong, Xie Heping, Ju Yang. Calculation Method of Fractal Dimension for 2-D Digital Image [J]. Journal of China University of Mining & Technology, 2004, 33 (1): 19-24.
[19] 管孝艳,杨培岭,任树梅,等.基于多重分形理论的壤土粒径分布非均匀性分析[J].应用基础与工程科学学报,2009,17(2):196-205.
Guan Xiaoyan, Yang Peiling, Ren Shumei, et al. Heterogeneity Analysis of Particle Size Distribution for Loamy Soil Based on Multifractal Theory [J]. Journal of Basic Science and Engineering, 2009, 17 (2): 196-205.
[20] 周炜星,吴韬,于遵宏.多重分形奇异谱的几何特性Ⅱ.配分函数法[J].华东理工大学学报,2000,26(4):390-395
Zhou Weixing, Wu Tao, Yu Zundong. Geometrical Characteristics of Singularity Spectra of Multifractals Ⅱ Partition Function Definition [J]. Journal of East China University of Science and Technology, 2000, 26 (4): 390-395.
收稿日期:2015-12-29
基金项目:国家重点基础研究发展计划(973计划)(2015 CB 250900);新世纪优秀人才支持计划(NCET-13-1030)
作者简介:朱维伟(1993-),男,江苏南京人,硕士研究生,主要从事油气田开发研究工作。
DOI:10.3969/j.issn.1006-5539.2016.03.013
