我国沪深股市与债市联动性研究

何苏燕

(广东科技学院 财经系,广东 东莞 523083)



财政金融研究

我国沪深股市与债市联动性研究

何苏燕

(广东科技学院 财经系,广东 东莞 523083)

[摘要]利用SVAR模型,选取2012年1月4日到2015年9月28日的上证综合指数、深证综合指数以及中证全债指数的日收盘价的对数收益率为研究对象,探寻我国沪深股市与债市之间的联动性问题。通过Granger因果关系检验、脉冲响应及方差分解可知,沪深股市与债市之间虽然具有一定程度的联动性,但是联动性不大;股市和债市之间的相互影响程度是不对称的,债市对股市的影响大于股市对债市的影响;上海股市与债券市场之间的联动性更强。

[关键词]沪深股市;债市;SVAR模型;Granger因果关系检验

一、引言

股票和债券是目前大多数投资者所接受并且运用的很熟悉的两种金融资产。基于风险管理的需要,国内外已有学者对两个市场收益之间的联动性问题进行了研究,并取得了一系列的研究成果。

本文研究股市和债市之间的联动性主要从收益率的角度出发,原因如下:首先,指数的收益率比指数本身具有更优良的统计特性,学者们研究起来更方便;其次,股票价格指数和债券价格指数的变化只是数值大小的变化,不会发生正负号的变化,但是价格指数的收益率则不一样,它不仅可以在数值大小上发生变化,更有可能在正负号上产生变动。由此,我们认为从收益率的角度来研究两市的联动性,对于投资者来说更具有直观的可读性。

二、文献综述

Gebhardt和Hvidkjaer(2005)考察了股票和公司债券的相互作用。实证研究表明,投资公司债券和该家公司的股票之间存在动量溢出效应,即在过去几年里拥有高的股票收益率的公司在未来几年会拥有较高的债券收益率[1]。Campbell 和Taksler(2003)研究了股票的波动率对公司债券收益率的影响。通过对1963到1999年的标准普尔和穆迪债券收益率指数的运用,我们发现公司债券的收益率在股票波动率大时会变大[2]。Stefano和Kind(2006)使用仿射资产定价模型来给股票和债券一起定价。从该模型我们能够得到股票和债券收益率之间的内生相关性,同时也使我们能够解释经济的基本面如何影响股票和债券收益率之间的相关性[3]。王媛和李帆(2014)分析了中美两国各自股票市场与债权市场之间一定时期之内指数的变动趋势,并分别对两国之间的股票市场与债券市场的相关性进行了深入探讨。结果显示,无论是中美两国各自股市与债市之间或者两国之间都存在替代效应[4]。徐浩(2014)首先分析了银行间同业拆借市场、股票市场、债券市场相互作用的基础,然后通过实证分析得出了债券市场对股票市场的影响要大于股票市场对债券市场的影响,二者之间的相互作用是不对称的[5]。

三、实证研究

(一)数据选取及处理

1.数据选取

本文选取的样本区间为2012年1月4日到2015年9月28日的日收盘价为研究对象,共899个数据。同时,选取采用上证综合指数、深证综合指数以及中证全债指数的日收盘价的对数收益率为研究对象。我们将金融资产的对数收益率定义为如下形式:Rt=100ln(Pt/Pt-1),在该式中,Pt向我们展示了在t时刻该项金融资产的价格,Pt-1则展示了在t-1时刻该金融资产的价格。我们将该对数收益率放大100倍是为了方便书写,以免小数点过多,书写起来过于繁琐。上证综指日收益率、深证综指日收益率以及中证全债指数日收益率分别用上述公式计算得来,且分别用SH、SZ和ZZ表示。

至于数据的来源,本文选用了锐思(RESSET)金融研究数据库,该数据库包含了本文要研究的所有的数据。在获取了数据,对数据进行处理以及使用模型进行估计时,本文主要使用Eviews7.0来处理相关数据。

2.单位根检验

要对变量进行格兰杰因果检验之前,我们首先要确定变量是平稳的,否则可能出现“伪回归”现象。在本文的单位根检验中,我们采用的是ADF检验方法。表1归纳所示为上证综指、深证综指和中证全债指数日收盘价对数收益率序列进行ADF单位根检验统计表。由ADF检验统计表可知,上证综指、深证综指和中证全债指数日收益率序列ADF统计量小于ADF分别在5%、1%显著水平下的临界值,也就是说原假设是不成立的,换言之,也就向我们展示了变量是平稳的这一属性。

表1　各变量的单位根检验结果

3. Granger因果关系检验

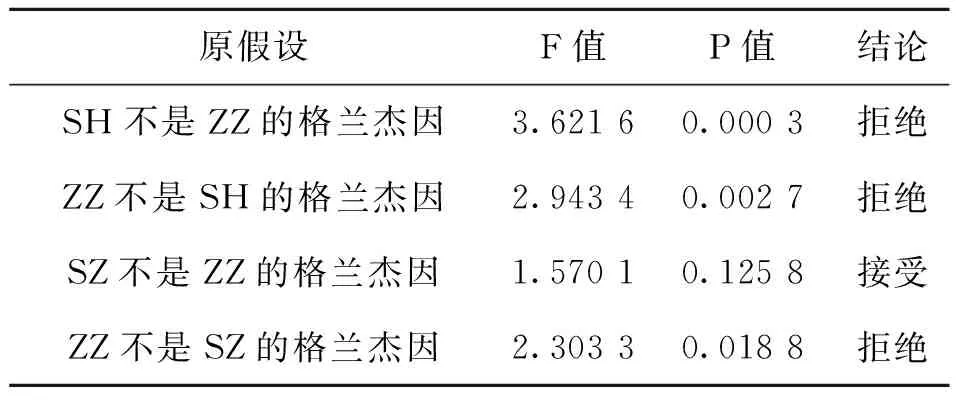
表2　股市与债市之间Granger因果关系检验结果

从表2我们可以看出,SH和ZZ之间有双向的Granger因果关系,两者互相能对对方产生较大的影响,而SZ与债ZZ之间相互的影响力比较薄弱,只有ZZ对SZ有较大的影响,反之,则没有。但是,纵观总体的检验情况,大体上我们可以认为股市和债市之间相互的作用力很大[6]。

(二)实证分析

本文在研究沪深股市和债市的联动性时,不仅要研究所有内生变量的滞后值对每一个内生变量的影响,而且还要研究所有内生变量相互之间的当期关系,AB 型的SVAR 模型能够帮助我们识别事先的研究目标,达到较好的拟合效果。

在构建AB 型的SVAR 模型之前,我们要对模型施加一定数量的约束条件, 这是模型可识别的一个前提。而对于本文中的3 元6 阶的SVAR 模型,我们需要对模型施加n(n-1)/2=3 个约束条件才能够使得模型恰好可识别[7]。

在SVAR 模型中,不同于VAR 模型的是,它有一个能够反应各个内生变量之间的当期之间的关系。我们假设这样的一个矩阵为A 矩阵,即:

债券市场市场的参与者有很多,其中最重要的参与者之一是商业银行,但是商业银行将其资金投放到股市的渠道是很迂回的,不是直接的。除了上面的这一点之外,一些机构投资者投资于股票市场的比例也受到严格的限制。这种资金在股市与债市之间流动的不对称就决定了资金可以更容易地从股市流入债市。 当股票市场上涨时,商业银行并不能顺利的即期进入该市场。此时,当商业银行想要将其能够支配的资金投放到股票市场时,往往只能通过一些渠道迂回地流入,这些渠道包括贷款给企业或者个人。这样,当商业银行要把资金投放到股票市场时,就产生了一个时滞,正是由于该时滞的存在,使得股市对债市的当期影响非常微弱,我们可以忽略不计,假设其为0。当债券市场的形势一片大好时,股票市场的资金流入债券市场的管道是顺畅的。股票市场几乎所有的投资主体都可以将其资金自由地投放到债券市场。由此我们认为债券指数对股票指数存在一定的影响[8]。

基于此,我们假设:b31=0,b32=0从理论上来说,沪深股市之间存在联动性。其相同的参与主体、处于共同的宏观经济基本面以及两市之间资金流的相互作用等都为两市联动提供了基础。表3为上证综指收益率与深证综指收益率之间的Granger 检验结果。由表3可知:SH 与SZ 之间互为Granger 因果。这也就意味着同期的上证综指和深证综指之间存在一定的关联, 我们假设SH 与SZ 之间呈现简单的一元线性相关关系,即:sz=b0+b21sh+εt.

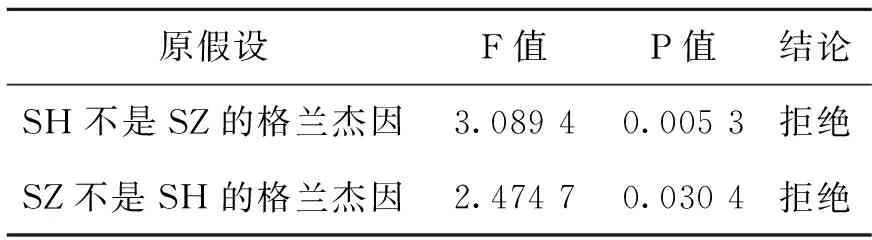
表3　上证综指收益率与深

用Eviews7.0得出:b21=0.957,代入A矩阵,得出

1.模型的建立

在构建模型之前,通过EVIEWS 软件来对数据进行拟合,选择出一个合适的滞后的阶数。这个滞后阶数的选择对SVAR模型的构建至关重要。在拟合滞后阶数过程中,有很多个指标提供了多个滞后阶数,此时所选择的滞后阶数时,要保证模型的滞后阶数足够大的同时也不能够让滞后阶数太大。因为当模型滞后阶数足够大时,能够更好的反映文中所构建的模型的动态特征。此外,如果我们所选择的滞后阶数非常非常大时,会无形中增加许多待估的参数,这些待估参数的增加会在很大程度上降低模型的自由度。本文对模型的滞后阶数进行确定是综合考察了上述两方面的内容。表4为通过Eviews 软件拟合的模型的滞后阶数,我们将模型的滞后期选为6。

在数据的平稳性检验通过以及模型的滞后阶数确定之后,我们建立一个三变量的SVAR 模型,此时的三个内生变量分别为SH、SZ、ZZ。将数据带入EViews 软件中操作得出的估计结果为:b12=0.310,b13=-0.176,b23=-0.121。但是我们比较关注的是债券指数对股票指数当期的影响,即b13和b23。经比较我们发现:当期的债券指数对当期的上证指数和深证综指均能产生一定负向的影响,且债券指数对上证指数的影响比对深证综指的影响大。

计量经济学认为对SVAR 模型中的单个参数值很难做出合理的解释,由此计量经济学家想出了一些方法来帮我们从该SVAR 模型中得出有用的结论,即可以通过观察其脉冲响应函数和对其进行方差分解来得出。

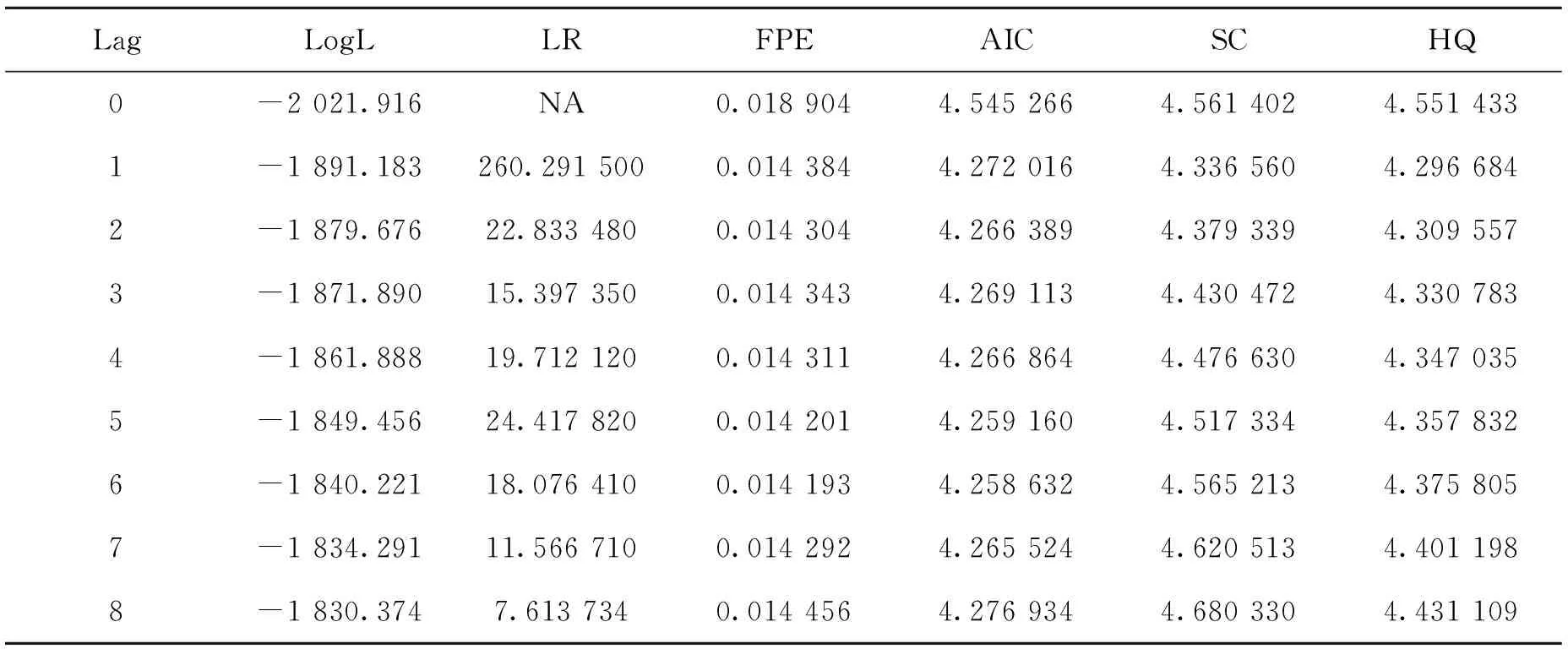
表4　模型滞后期判定结果

在进行脉冲响应和方差分解之前,首先要对模型的稳定性进行检验。稳定性检验的通过才意味下面一系列检验的前提实现了。图1表明,该模型通过了稳定性检验。

2.脉冲响应

从图2我们可以看出,给中证全债指数日收益率一个正的冲击经市场传递会对上证综指日收益率产生影响,且在前3期,该正的冲击会给上证综指日收益率一个先增大后减小的负向的影响,该负向的影响最大可以达到5%。在第3期转化为正向的影响,最大达到8%。在之后的期间,影响始终为正的,且该正面影响逐渐减小。

图1　SVAR模型的稳定性检验

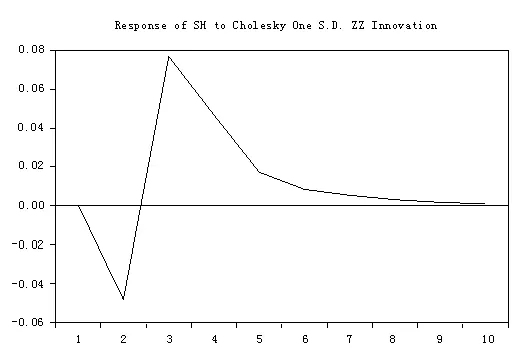
图2　上海股市对债券市场一个标准差新息的响应

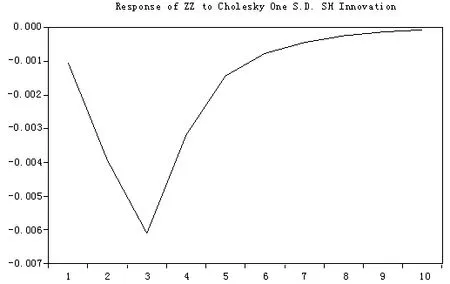
图3　债券市场对上海股市一个标准差新息的响应

从图3我们可以看出,给上证综指收益率一个正的冲击也会经过市场传递给债券市场,且该正的冲击给中证全债指数带来的几乎全是负的影响。在前三期,该正的影响逐渐增大,最大达到0.6%。从第3期开始,该负面的影响慢慢地减小。

图4　深圳股市对债券市场一个标准差新息的响应

从图4我们可以看出,当我们对中证全债指数施加一个正的随机干扰项的冲击时,在前2期对深证债券综指有一个先增大后减小的负面的影响,且该负面的影响在第2期实现最大,约为3.5%。在第3期,该影响的方向发生了质的转变,在第4期和第5期转变为负的影响,并且在这时,正向的影响达到最大,为5%。之后的期间,该正的影响逐渐地削弱。

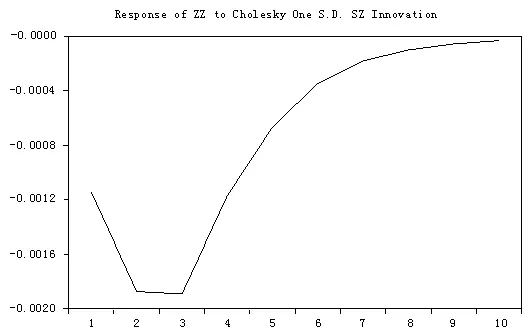
图5　债券市场对深圳股市一个标准差新息的响应

从图5我们可以看出,给深证综指收益率一个正的冲击也会经过市场传递给债券市场,且经过传递之后带来的效应都是负向的效应。该负向的效应在前3期逐渐增大,最大达到-0.2%,在之后该影响逐渐削弱。

3.方差分解

表5　上证综指日收益率的方差分解

从表5可以看出,上证综指收益率的波动主要受自身波动的影响,即使在第10个交易日,其波动仍有94.42836%由自身解释,只有2.43081%由债券市场的波动解释。从表6可以看出,深证综指收益率的波动主要受其自身波动的影响,即使在10个交易日,也有69.78262%由深圳股市自身的波动解释,只有1.175725%由中证全债指数收益率波动解释。

表6　深证综指日收益率的方差分解

综合表5和6,我们可以看出上证综指和深证综指日收益率的波动均主要受自身的影响,但是中证全债指数日收益率的波动对上证综指的影响比对深证综指的影响大。

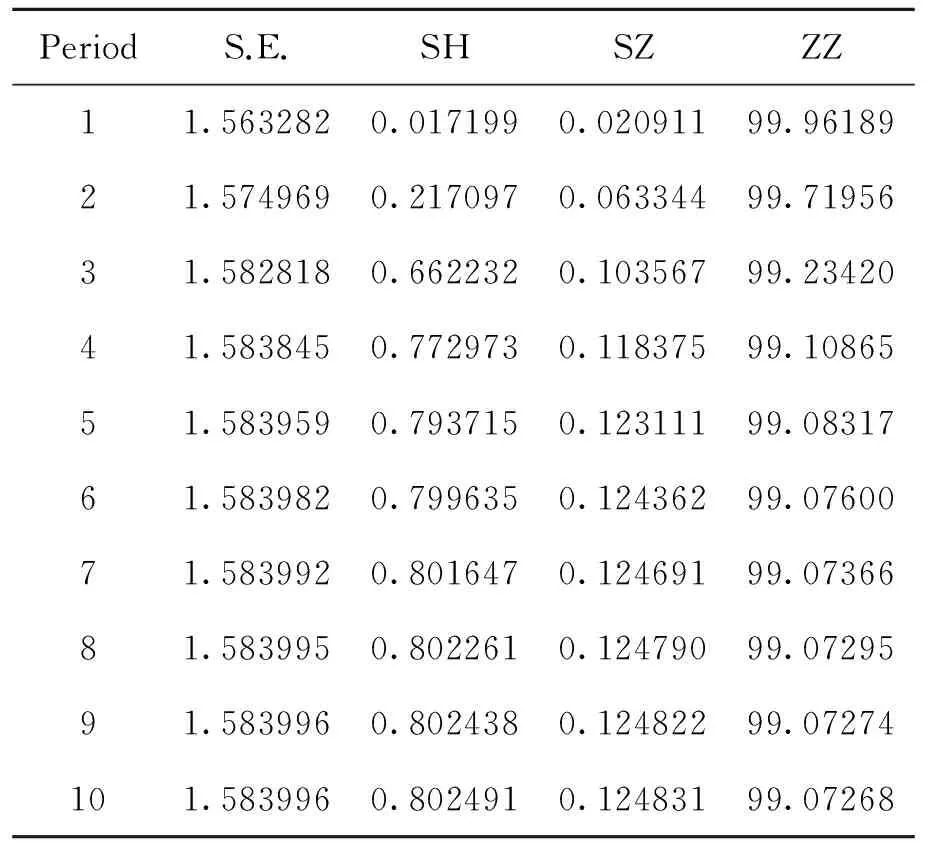
表7　中证全债指数日收益率的方差分解

从表7我们可以看出,债券市场的波动也主要受自身波动的影响,即使在10个交易日,也有99.07268%由中证全债指数自身的波动解释,只有0.802491%由上证综指日收益率的波动解释,另外0.124831%由深证综指日收益率波动解释。由此,我们可以看出债券指数的波动组要受其自身影响,但是上证综指日收益率的波动对债券指数的影响比深证综指日收益率的波动对其的影响大。

四、结论

在本文实证检验的过程中,我们选择收益率这一角度作为切入点来实现本文的研究目的。在实证过程中,我们所使用的三组收益率序列,分别是:上证综指收益率(SH)、深证综指收益率(SZ)和中证全债指数收益率(ZZ)。在结构向量自回归模型(SVAR)的基础上,采用脉冲响应函数、方差分解以及Granger因果关系检验来检验中国股票市场和债券市场之间的联动,可以得出以下结论:

第一,沪深股市与债市之间虽然具有一定程度的联动性,但是联动性不大。

第二,债券市场对上海股市的影响比上海股市对债券市场的影响大;深圳股市对债券市场的影响比债券市场对深圳股市的影响大。即,两市之间相互作用力的大小不尽相同,债市对股市施加的作用力的强度明显地大于股市对债市施加的作用力的强度。

第三,上海股市对债券市场的影响比深圳股市对债券市场的影响大;债券市场对上海股市的影响比债券市场对深圳股市的影响大,即,上海股市与债券市场之间的联动性更强。

上证综指的样本股是沪市的全部上市股票,该指数反映在上海证券交易所挂牌股票价格的总体走势,截至2015年9月30日,在上海证券交易所上市的公司有1 071家,在这1 071家上市公司中,绝大多数是大中型企业,其拥有的资金非常雄厚,公司的稳定性很强;而通过对深证综指的样本股的解析,我们发现这些样本股包罗了在深圳主板市场、中小板市场以及创业板市场上市的所有股票,截至2015年9月30日,在深交所主板市场上市的公司只有478家,中小板上市的公司有767家,创业板上市的公司有484家,在深圳证券交易所上市的公司有70.75%为中小企业。对比沪深证券交易所上市的公司类型,我们可以认为上海证券市场的风险比深圳证券市场的风险小。

对于中国这样一个发展中国家来说,我们的人均收入比国外的发达国家少了一大截,正是由于手上所拥有的资产有限,导致了他们非常的厌恶损失。对于在两市之间都可以灵活投资的投资者,在他们选择投资产品时,往往将经济形势与自身的风险承受水平综合考虑,他更可能会将资金在债券市场和上海股市之间进行转移,而不是在债券市场和深圳股市之间进行转移。因此,上海股市与债券市场之间的联动性大于深圳股市与债券市场之间的联动性。

[ 参 考 文 献 ]

[1] Gebhardt W R, Hvidkjaer S, Swaminathan B. Stock and bond market interaction: Does momentum spill over?[J]. Journal of Financial Economics, 2005, 75(3): 651-690.

[2] Campbell J Y, Taksler G B. Equity volatility and corporate bond yields[J]. The Journal of Finance, 2003, 58(6): 2321-2350.

[3] Stefano d’Addona, Kind A H. International stock—bond correlations in a simple affine asset pricing model[J]. Journal of Banking & Finance, 2006, 30: 2747-2765.

[4] 王媛,李帆.股票市场与债券市场相关性研究[J]. 武汉大学学报, 2014,(4): 265-269.

[5] 徐浩.银行间同业拆借市场与股票市场、债券市场间相关性的实证研究[D]. 武汉:华中师范大学,2014.

[6] 高铁梅.计量经济分析方法与建模:EVIEWS应用及实例[M].北京:清华大学出版社,2009.

[7] 李子奈.计量经济学(第3版)[M]. 北京:高等教育出版社,2010.

[8] 袁超,张兵,汪慧建.债券市场与股票市场的动态相关性研究[J]. 金融研究, 2008,(1): 63-75.

[责任编辑:刘炜]

doi:10.3969/j.issn.1672-5956.2016.03.015

[收稿日期]2015-10-27

[作者简介]何苏燕,1990年生,女,湖北荆门人,广东科技学院助教,硕士, 研究方向为投资学,(电子信箱)hesuyan555@163.com。

[中图分类号]F832.5

[文献标识码]A

[文章编号]1672-5956(2016)03-0091-06