基于SVD-LCD与1.5维谱的滚动轴承故障诊断
2016-07-26崔伟成李伟孟凡磊刘林密
崔伟成, 李伟, 孟凡磊,刘林密
(海军航空工程学院 飞行器工程系,山东 烟台 264001)
滚动轴承发生故障时,其振动信号具有故障特征微弱,非平稳、非线性等特征,准确地进行故障诊断较为困难。因此,最大限度的提高测量信号的信噪比,并研究适用于非平稳信号的时频分析及故障特征提取方法具有重要的工程意义。
奇异值分解( Singular Value Decomposition,SVD) 降噪是一种非线性滤波方法,具有良好的稳定性和不变性,可以有效降低信号中的噪声,提高信噪比[1-2]。为准确分解信号,得到分量的局部特征,众多学者开展了时频分析技术的研究[3-5],并在本征时间尺度分解的基础上创造性的提出了局部特征尺度分解(Local Characteristic-Scale Decomposition,LCD)[6-8]。LCD在保证分解所得分量物理意义清晰的基础上,具有计算时间短、端点效应不明显等优势,开拓了自适应时频分析方法的新思路[9]。1.5维谱是一种降维的高阶累积量谱,对高斯噪声不敏感,理论上可以完全抑制高斯噪声和非高斯的有色噪声,同时又能保持非线性系统的相位信息[10-13]。
为了准确得到轴承故障振动信号内含的故障特征信息,首先采用SVD降噪技术提高信号的信噪比,然后对降噪信号进行LCD,并将分解后的内禀尺度分量(Intrinsic Scale Components,ISC)进行Hilbert变换求包络信号,最后应用1.5维谱技术提取故障特征,给出诊断结果。
1 基本理论
1.1 奇异值分解降噪
SVD 降噪的原理基于相空间重构,利用信号与噪声的能量可分性,对含噪信号构成的矩阵进行分解,仅保留信号特征奇异值,达到去除噪声目的[1-2]。
1.1.1 嵌入
设原始信号为X=[x1,x2,…,xN],利用相空间重构理论重构的吸引子轨迹矩阵为
,(1)
式中:A为m×n阶的Hankel矩阵;τ为延迟步长;n=N-(m-1);m为嵌入维数。
1.1.2 奇异值分解
对(1)式进行其奇异值分解得
(2)

1.1.3 分组
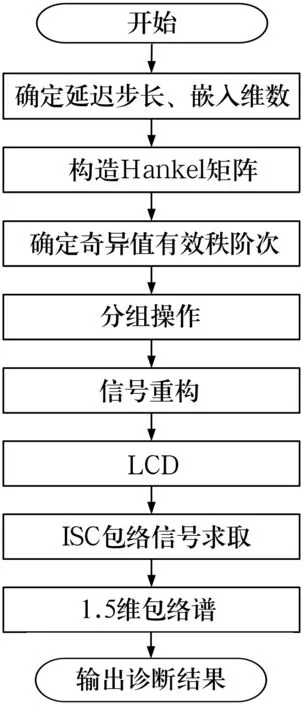
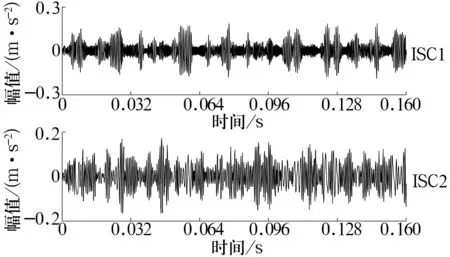
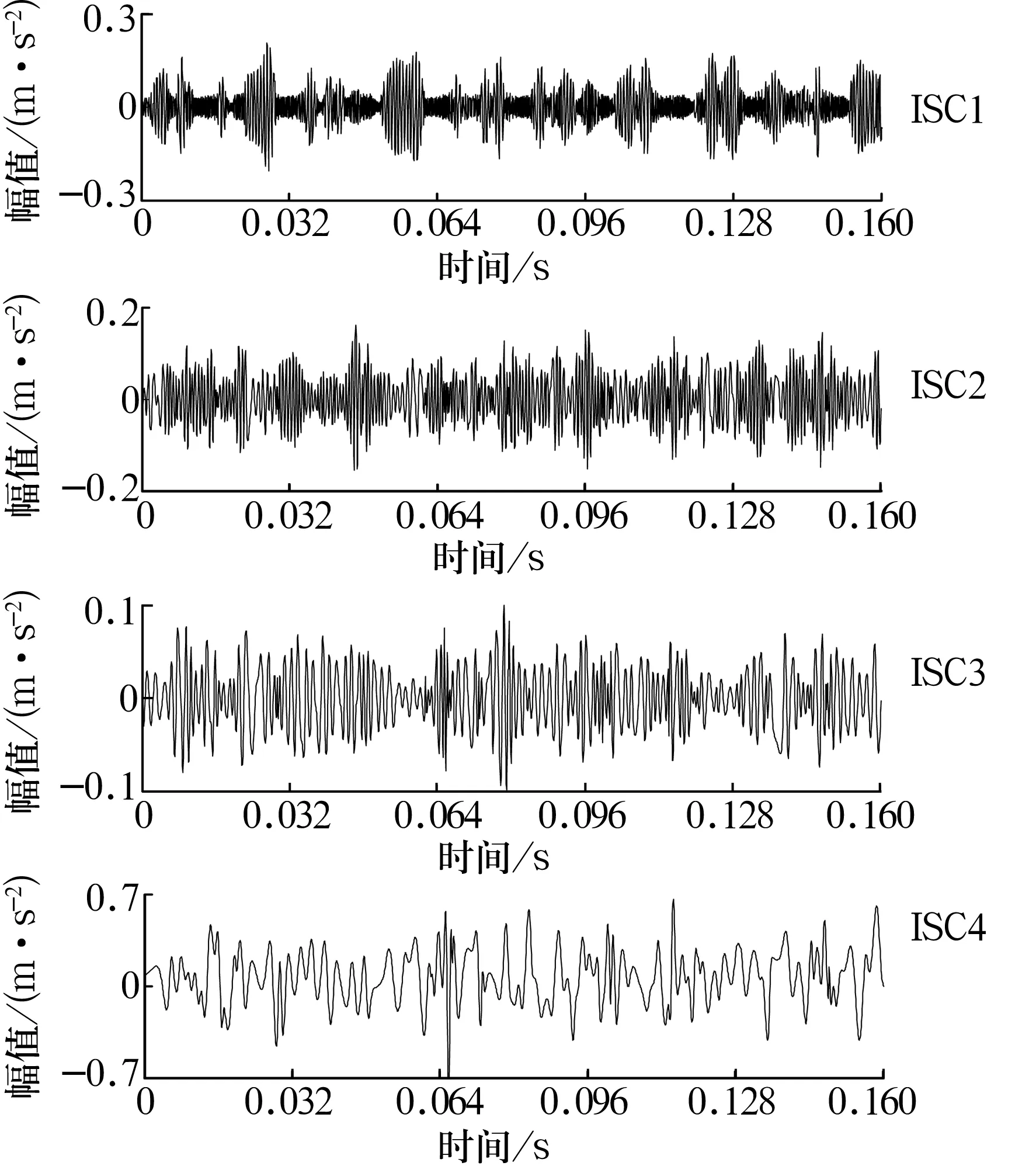
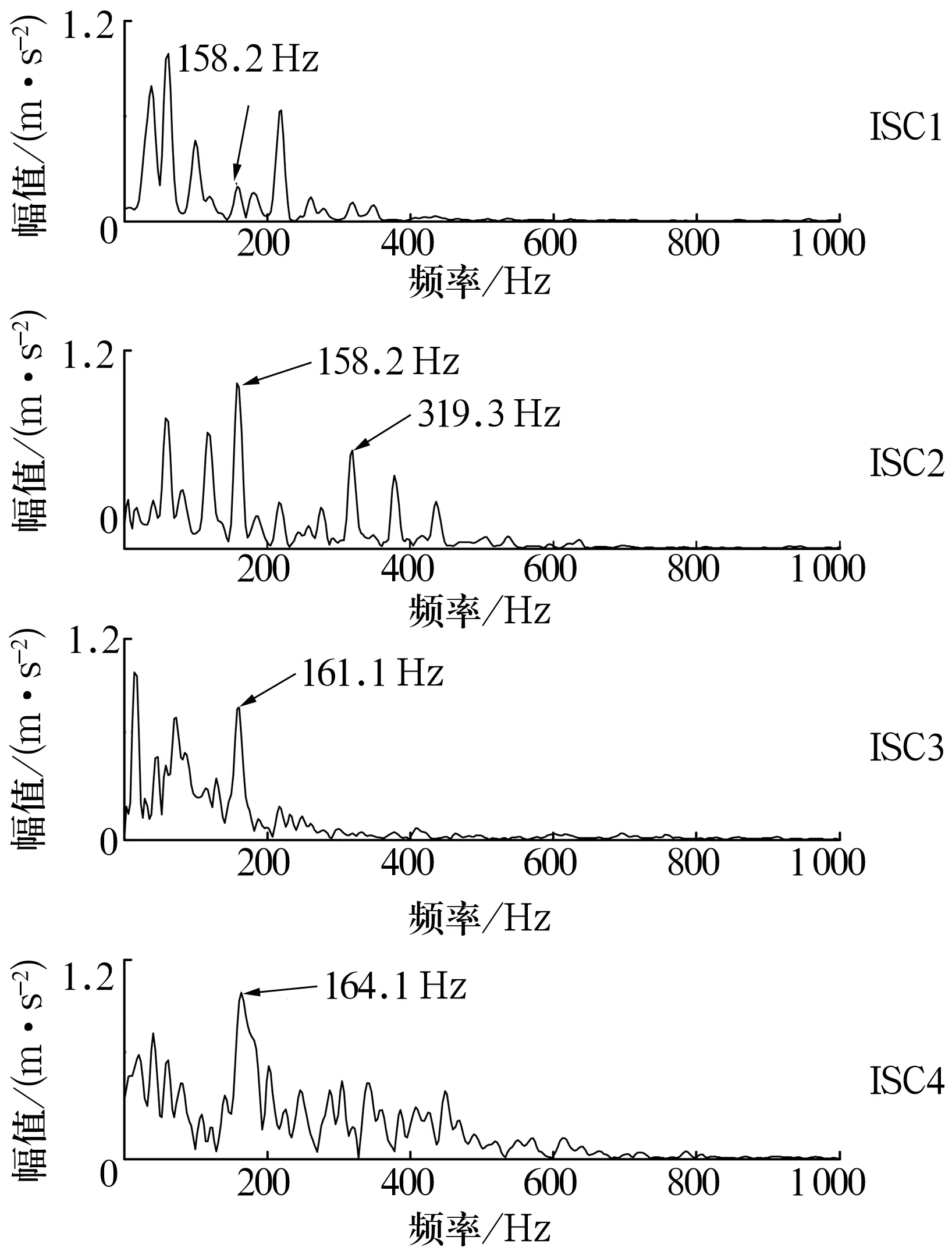
对于分解得到的奇异值,认为前r(r 1.1.4 对角平均化 对角平均化的目的是将上述分组得到的信号矩阵转化成长度为N的序列,即由信号分量重构信号。 1.2.1 内禀尺度分量 LCD方法假设任何复杂信号均由不同的ISC组成,并且各ISC之间相互独立。 LCD实质就是将任意信号x(t)分解成若干个ISC之和,从而达到对信号分解的目的。每个ISC必须满足2个条件: 1)在整个数据段内,任意2个相邻的极值点符号互异。 2)在整个数据段内,设所有的极值点为Xk,对应的时刻为τk(k= 1,2,…,M;其中M为极值点的个数)。取任意2个相邻的极大(小)值点(τk,Xk)和(τk+2,Xk+2)可构成τk+1时刻的一个函数值,即 (3) 则Ak+1与其对应的极大(小)值Xk+1的比值关系不变,即 aAk+1+(1-a)Xk+1=0, (4) 式中:a∈(0,1),为一常量,典型地a=0.5。 这2个条件保证了相邻极值点之间的单调性,即波形的单一性;同时保证了所获得ISC波形的光滑性和对称性。从而使每个ISC在任意的极大值和极小值之间具有单一的模态,可以局部地与正弦曲线相吻合,使得瞬时频率具有了相应的物理意义。 1.2.2 分解过程 根据ISC的定义,对任意实信号x(t)进行LCD的过程为: 1)确定信号x(t)的所有极值点Xk及对应的时刻τk(k= 1,2,…,M)。对2个时间序列进行延拓,延拓方式为两端各增加一个极值点,即 (5) (6) 延拓后的时间序列分别为Xk,τk(k= 0,1,…,M+1)。 2)设置参数a的值,基线控制点计算式为 Lk+1=aAk+1+(1-a)Xk+1= 3)计算基线信号段 (8) 式中:Hk(t)为对原始信号的第k个区间进行线性变换得到的基线信号段。 4)由Hk(t)依次连接成基线信号H1(t),并将H1(t)从原始信号中分离,即 h1(t)=x(t)-H1(t)。 (9) 若h1(t)是ISC,输出I1(t)=h1(t)。否则将h1(t)作为原始信号将步骤1~4重复循环k-1次,得到I1(t)=h1k(t)。 5)将I1(t)从信号x(t)中分离,可得新的剩余信号 r1(t)=x(t)-I1(t)。 (10) 6)将r1(t)视为原始数据,将步骤1~5重复循环n-1次,直至rn(t)单调或者为一常数。这样就将x(t)分解为n个ISC和1个剩余信号之和,即 (11) 1.5维谱定义为3阶累积量对角切片的Fourier变换[10]。对于零均值平稳随机过程x(t),其三阶累积量定义为 c3x(τ1,τ2)=E[x(t)x(t+τ1)x(t+τ2)], (12) 式中:E为数学期望;τ1,τ2为不同的时间延迟。 令τ1=τ2=τ,得到三阶累积量的主对角切片为 c(τ)=c3x(τ,τ)=E[x(t)x(t+τ)x(t+τ)]。 (13) 对c(τ)进行一维Fourier变换可得x(t)的1.5维谱,即 (14) 由上述定义可看出,1.5 维谱为双谱在一维频率空间上的投影。由于零均值高斯噪声的三阶累积量值为零,1.5 维谱相对于双谱不仅计算量减小,还保留了双谱对随机噪声的抑制作用和非二次相位耦合谐波的剔除能力。 基于SVD-LCD与1.5维谱的滚动轴承故障诊断方法基本流程如图1所示。首先,结合相空间重构技术构造振动信号的Hankel矩阵,对Hankel矩阵进行SVD降噪,确定奇异值有效阶次并将原始信号分成信号分量和噪声分量,对信号分量重构得到降噪信号;然后,对降噪后的信号进行LCD,得到若干ISC,将分解后的ISC进行Hilbert变换得到包络信号;最后,求取包络信号的1.5维谱,进行故障特征提取。 图1 故障诊断流程图 SVD降噪的关键参数有Hankel矩阵的构造参数及奇异值有效秩阶次。 1)Hankel矩阵的构造涉及2个重要参数:延迟步长τ和嵌入维数m,在此选取τ=1,m=N/2[1]。 2)奇异值有效秩阶次采用奇异值均值法确定,即将所有低于奇异值平均值的奇异值置零[2]。 1)标准LCD算法采用分段线性方法,由基线控制点计算基线信号。为了得到更光滑的ISC,采用三次样条方法替代分段线性方法。 2)ISC判据采用标准偏差判据[6-9]。 3)终止条件选用剩余信号能量判据[6-9]。 试验数据来自美国凯斯西储大学电气工程实验室[14]。试验轴承为6205-2RS型深沟球轴承,该轴承的尺寸参数见表1。 表1 6205-2RS的尺寸参数 试验中采用加速度传感器采集振动信号,采样频率fs=12 kHz,采样点数取N=2 048。使用电火花加工技术在该轴承内圈上布置了单点故障,故障直径为0.177 8 mm,该轴承用于支承电机轴,电动机转速为1 772 r/min,计算得轴承内圈点蚀故障特征频率为159.96 Hz。 原始信号的时域波形和频谱如图2所示(为清晰展现故障特征,只给出0~1 000 Hz频段的频谱)。从图中可以看出:时域波形的信号比较杂乱,不易发现周期成分;频谱上隐约可以看见158.2 Hz处存在谱线,考虑到计算误差,可近似认为158.2 Hz即为轴承内圈故障特征频率,但特征很不明显。 图2 原始信号的时域波形及频谱 直接对原始采样信号进行LCD,得到2个ISC分量和1个剩余信号。2个分量的时域波形如图3所示,从图中可以看出:2个分量的频率段没有明显差别,分解产生了明显的模态混叠;而且未发现低频分量,分解不够彻底。 图3 原始信号LCD后的ISC时域波形 应用Hilbert变换求取各ISC的包络谱,其低频段如图4所示。从图中可以看出:1)分量1在164.1 Hz处存在谱线,但不够突出;2)分量2在158.2 Hz处存在较为清晰的谱线,但不是最大谱峰;3)在2个分量包络谱中,特征频率倍频处未发现明显的谱线,不易给出是否轴承内圈故障的结论。 图4 ISC的包络谱 对原始采样信号进行SVD降噪处理并进行LCD,得到4个ISC和1个剩余信号。4个ISC的时域波形如图5所示,从图中可以看出:LCD类似于自适应的滤波器,4个ISC所包含的频率段逐渐降低,模态混叠现象得到了明显的抑制;而且分量4的幅值明显小于原始信号,从能量的角度来看,分解较为彻底。 图5 原始信号SVD-LCD后的ISC时域波形 求取各个ISC的Hilbert包络谱,其低频部分如图6所示。从图中可以看出:1)在分量1的包络谱中,158.2 Hz处存在较为清晰的谱线,虽不是最大谱峰,但其特征比原始信号LCD的分量1包络谱明显;2)在分量2的包络谱中,158.2 Hz处的谱线存在明显的谱峰,并且在特征频率2倍频(316.4 Hz)处的谱峰也清晰可见;3)在分量3的包络谱中,158.2 Hz处的谱线是全谱最大峰值,故障特征明显;4)在分量4的包络谱中,164.1 Hz处的谱线也相对清晰。将4个谱图相互印证,可得出内圈故障的结论,与事实吻合。可见,SVD降噪可以降低LCD的模态混叠效应,使分解更彻底,得到的分量更能体现信号的特征,是一种有效的LCD预处理方法。 图6 原始信号SVD-LCD后的ISC包络谱 对4个ISC的包络信号取1.5维谱,其低频部分如图7所示。从图中可以看出:1)在分量2的1.5维谱中的158.2和319.3 Hz处,以及分量3的1.5维谱中的161.1 Hz处均存在清晰谱峰,并且比包络谱清晰;2)分量4的1.5维谱中,164.1 Hz谱线是全谱最大峰值;3)1.5维谱的噪声能量远远小于包络谱;4)1.5维谱的计算过程中会引入误差,可能会使特征频率及其倍频发生偏移,在使用时要引起注意。 因此,包络谱体现的故障特征均可由1.5维谱体现,并且1.5维谱体现的故障特征更明显,抗噪能力更强。可见1.5维谱是一种有效的LCD后处理方法。 图7 原始信号SVD-LCD后ISC的1.5维谱 以局部特征尺度分解为基础,考虑噪声的影响,提出了一种新的滚动轴承故障诊断方法。该方法通过奇异值分解降噪预处理,提高LCD的质量和准确性,通过1.5维谱后处理,进一步抑制噪声,突出故障特征。以滚动轴承内圈点蚀故障振动信号为对象,验证了该方法提取故障信号的有效性,该方法也可推广至齿轮等旋转机械故障诊断领域,具有一定的工程应用价值。1.2 局部特征尺度分解
1.3 1.5维谱
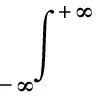
2 基于SVD-LCD与1.5维谱的滚动轴承故障诊断
2.1 SVD降噪参数
2.2 LCD算法
3 试验分析




4 结束语
