中央稳定板提高颤振稳定性能的细观作用机理
2016-07-26欧阳克俭陈政清
欧阳克俭, 陈政清
(1.国网湖南省电力公司 电力科学研究院,长沙 410007; 2.湖南大学 风工程研究中心,长沙 410082)
中央稳定板提高颤振稳定性能的细观作用机理
欧阳克俭1,2, 陈政清2
(1.国网湖南省电力公司 电力科学研究院,长沙410007; 2.湖南大学 风工程研究中心,长沙410082)
摘要:通过CFD数值模拟以及PIV风洞试验研究了中央稳定板对矮寨桁架梁悬索桥断面绕流的细观作用机理。CFD数值模拟表明中央稳定板促进了在桥面中央附近形成位于上下桥面的旋涡对,使之相当于升力的作用。有稳定板断面前端和尾部的旋涡体积增大,进而使桥梁断面在颤振中的竖向自由度参与作用增强。PIV流迹显示气流在中央稳定板的背风侧形成了漩涡,在模型尾部同样有旋涡的形成,进一步验证了CFD数值模拟的正确性。
关键词:颤振;气动措施;中央稳定版;PIV;CFD
气动控制措施对颤振性能的细观作用机理主要有粒子图像测速技术(Particle Image Velocimetry)简称为PIV和CFD两种方式。Palombi等[1]对大海带东桥以及不同类型的矩形断面进行了PIV试验,分析了断面的旋涡大小、强度、间距以及涡迹特征。张伟等[2-3]基于同济大学专用的PIV风洞试验室对一些典型断面的颤振机理进行了系统的研究。刘祖军[4]通过PIV试验发现静场绕流的箱梁断面在尾部有尺度较大的旋涡,接近圆形,风嘴和模型下底部是旋涡产生的主要部位。Larsen[5]通过离散涡的CFD分析方法对Tacoma桥梁断面的简化模型进行了颤振机理方面的研究。Watanabea等[6]基于CFD方法研究了中央开槽对三分力系数的影响,得到了模型表面的压力分布,该方法仅考虑了中央开槽对静力系数的影响。Sarwar等[7]通过CFD方法分析了导流措施对高墩类矩形断面气动性能的影响,研究发现导流措施能够很好的抑制结构的振动幅值。
位于湖南西部山区的吉首至茶洞公路段的矮寨大桥为一座钢桁加劲梁悬索桥,该桥设计方案不能满足颤振检验风速的要求[8-9]。本文即以矮寨大桥为研究背景,对中央稳定板提高该桥颤振稳定性的细观作用机理进行研究,首先根据CFD数值模拟,研究了中央稳定板对桁架断面旋涡的的作用规律,从细观的角度对中央稳定板提高桁架梁悬索桥的颤振性能进行剖析;然后基于PIV风洞试验[10-11],对矮寨大桥节段模型绕流流场进行了研究。PIV风洞试验和CFD数值模拟研究结果互相比对,校核结果。
1CFD数值模拟研究
鉴于桥梁节段模型试验是基于片条理论假设[12-14],为节省计算工作量,本文将桁架模型进行一定的简化,使之满足二维数值计算的要求。具体简化方法为:将贯通全桥的主桁、上下稳定板、工字梁、中央稳定板、检修轨道底板按横桥向截面截取;将桥面栏杆进行风阻面积等效;上下平联和斜腹杆按在每个桁架段空间交错的中心位置近似截取。有稳定板简化模型如图1所示,无稳定板计算模型简化类似。有无中央稳定板两种模型都封闭了中央开槽。
矮寨大桥断面CFD模型尺寸和风洞节段模型试验尺寸相同。模型宽度B=0.54 m。入口距断面中心8B,出口距断面中心16B,入口采用速度入口边界条件,出口为压力出口边界条件,上下壁面采用自由滑移壁面边界条件,模型断面采用无滑移的壁面边界条件,风攻角为0°,边界条件具体设置如图2。当入口风速为10 m/s时。当风速为10 m/s,SST湍流模型计算得到的升力系数的频谱曲线如图3所示,其中频率信息显示含有14.8 Hz、8.2 Hz、24.2 Hz等成分。

图1 有稳定板二维简化模型Fig.1 Two dimensional simplified numerical model of the Central stabilizer


图2 二维桁架模型计算域及边界条件Fig.2Computationaldomainandboundaryconditionsoftwodimensionaltrussmodel图3 有稳定板模型升力时程幅值谱Fig.3Lift-timecurveofmodewithcentralstabilizer
从升力时程曲线可以看出SST湍流模型对旋涡脱落的捕捉能力明显强于k-ε湍流模型。两种湍流模型计算得到的平均三分力系数和试验的对比结果如表1所示,k-ε模型三分力系数的计算结果和试验值较为接近,尤其是扭矩系数正负号和试验值一致。从三分力系数的CFD数值模拟结果可以看出,对于矮寨大桥模型断面的简化处理是合理有效的,完全满足计算精度要求,只是在湍流模型的选择上要有针对性。

表1 有稳定板0°攻角三分力系数对比
分别基于SST和k-ε两种湍流模型计算了有无稳定板的模型断面在风速为6 m/s和10 m/s时的平均流场。图4和图5为有稳定板的断面的流线显示,无稳定板断面模型和有稳定板断面模型的计算工况一致,无稳定板断面模型的流线显示如图6和图7所示。
从图4的平均流场可以看出,气流首先穿透迎风侧的防撞栏杆,进入前半桥面,在前半桥面的上表面和下表面周围区域没有形成旋涡,流线较为光滑。气流绕过上下稳定板时在上下稳定板的背风侧都有一个和稳定板等高的旋涡形成,后半桥面的上部气流穿过下游防撞栏杆进入尾流区域。后半桥面的下部气流在穿过桥面板底部从下游主桁上弦穿出时形成的气流剪切且冲击穿透上部栏杆的气流作而形成了一个体积较小的旋涡。在模型断面的其他区域流线都很光滑,没有旋涡生成。尽管两图反映的风速不同,得到的流场变化基本一致。图5的流线显示在上下中央稳定板的背风侧形成有旋涡对,但是在模型尾部没有观察到旋涡的形成,这也说明由于近壁面网格处理和计算的原因,SST湍流模型对旋涡的扑捉能力较k-ε湍流模型更强。对于无稳定板的情况,图6得到的两个不同风速的流线显示图基本一致,在此一并说明。首先气流从上游主桁上弦和桥面板的间距之间进入下桥面,此时可以看出,几个“工”字型纵梁之间的小旋涡连成一个整体,也即在迎风侧桥面板的底部形成一个体积较大的旋涡。上桥面气流穿透所有栏杆进入尾流。下部桥面气流在穿过桥面板底部从下游主桁上弦穿出时形成的气流剪切且冲击穿透上部栏杆的气流作而形成了一个体积较大的旋涡。由图7所示k-ε湍流模型在两个风速下没有捕捉到旋涡。综合对比有无稳定板模型由SST湍流模型得到的计算结果:无稳定板模型在桥梁断面的迎风侧和尾部都发现了明显的旋涡,且旋涡的体积较大,而在有稳定板的计算工况中没有发现桥梁模型在迎风侧有旋涡形成,只在模型尾流区域有体积较小的旋涡生成,更为明显的是有稳定板模型在靠近模型的中间位置,也即稳定板的背风侧形成了一个上下旋涡对。初步分析,由于没有稳定板的模型在迎风侧和尾流区有明显的旋涡形成,这对旋涡可能交替作用桥梁模型,产生一个扭矩作用,从而诱使桥梁颤振的发生。而有稳定板的作用时,迎风侧桥面底板没有过大的旋涡,相应的在尾流区域也只有相对较小的旋涡,从而使得气流对桥梁的力矩作用减弱。在靠近模型中央,也就是上下稳定板的背风区域形成了明显的旋涡对,这使得旋涡的交替作用相当于气动升力的形式,使得桥梁竖向自由度的参与程度增强而扭转自由度的参与程度减弱,进而达到提高颤振临界风速的目的。这和前期研究中中央稳定板的宏观机理解释吻合[8-9]。
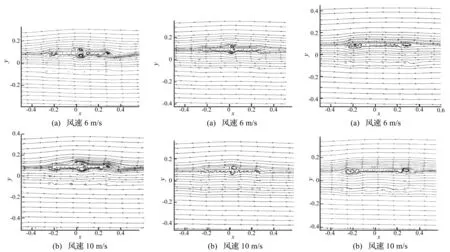

图4 有稳定板模型稳态流线(SST湍流模型)Fig.4Steadystreamlineofmodewithcentralstabilizer(SSTturbulencemodel)图5 有稳定板模型稳态流线(k-ε湍流模型)Fig.5Steadystreamlineofmodewithcentralstabilizer(k-εturbulencemodel)图6 无稳定板模型稳态流线(SST湍流模型)Fig.6Steadystreamlineofmodewithoutcentralstabilizer(SSTturbulencemodel)
2PIV风洞试验
矮寨大桥主梁断面缩尺比1∶50,节段模型固定于风洞内部,如图8所示。CCD相机镜头产自尼康公司,焦距为85 mm,光圈为1.4,相机的有效像素是1 100 万像素,最大分辨率为4 000×2 672 像素,每个像素的尺寸为9 μm×9 μm。采样频率为5 Hz,试验采用的激光波长为532 nm的绿光。

图8 矮寨大桥节段模型PIV试验Fig.8 PIV wind test of section model of aizhai bridge
由于矮寨大桥模型桥面以下为桁架交错结构,这将遮挡CCD相机对激光面位置流场的有效拍摄,故本次试验只进行了0°攻角模型上表面和尾部流场的PIV风洞试验。由于桥梁模型相对相机拍摄面过宽,同时也为保证相机拍摄区域为激光投射能量的集中区域,特将模型上表面和模型尾部分成两个工况进行试验,节段模型通过刚性固定于湖南大学Ⅱ风洞试验高速段。
当激光投射到模型表面时,白色的塑料材质栏杆和木质桥面板会产生反射和散射,影响相机对流场的有效捕捉,为尽量降低这一因素的影响,在激光面投身区域附近喷洒了亚光黑漆,使得曝光减少,拍摄效果得到明显改善。通过5次采集,每次连续采集20组图片后进行互相关的平均计算即可得到模型绕流的平均流场。进行了0°攻角,风速分别为6 m/s和10 m/s有无稳定板节段模型的静场绕流PIV风洞试验。
由图9的试验结果显示,风速为6 m/s时,有稳定板模型的上表面在中央稳定板的背风侧形成了一个明显的旋涡,这和CFD数值模拟结果一致,只是在体积大小上有所不同。速度云图说明迎风侧前半桥面上方的气流速度整体大于下游后半桥面,风速沿桥面往上呈梯度变化,这是由于桥面和桥面附属设施的粘性作用所致。以中央稳定板的高度作为参照物,发现PIV试验扑捉到的旋涡体积要小于CFD数值模拟结果。由图9、图11、图13、图15可知,有无稳定板的模型断面在下游防撞栏杆的附近均有体积细小的旋涡形成,这是在CFD数值模拟中所没有发现的,这也说明PIV试验对旋涡的捕捉能力要强于CFD中的SST湍流模型所计算的结果。图11显示无稳定板模型上中央防撞栏附近没有形成旋涡。图10、图12、图14、图16说明有无稳定板的模型断面尾部都有体积相对较大的旋涡形成,旋涡旋转方向为顺时针,该旋涡的形成是由于气流从下游主桁和桥面之间的间距冲出,形成的顺时针旋涡。这与CFD数值模拟得到的结论一致。

图9 有稳定板模型上表面平均流线和速度云图(风速6 m/s)Fig.9 Surface streamline and velocity cloud picture of mode with central stabilizer(6 m/s)

图10 有稳定板模型尾部平均流线和速度云图(风速6 m/s)Fig.10 Surface streamline and velocity cloud picture of tail of mode with central stabilizer(6 m/s)

图11 无稳定板模型上表面平均流线和速度云图(风速6 m/s)Fig.11 Surface streamline and velocity cloud picture of tail of mode without central stabilizer(6 m/s)

图12 无稳定板模型尾部平均流线 (风速6 m/s)Fig.12 Surface streamline and velocity cloud picture of tail of mode without central stabilizer(6 m/s)

图13 有稳定板模型上表面平均流线(风速10 m/s)Fig.13 Surface streamline and velocity cloud picture of tail of mode with central stabilizer(10 m/s)

图14 有稳定板模型尾部平均流线和速度云图(风速10 m/s)Fig.14 Surface streamline and velocity cloud picture of tail of mode with central stabilizer(10 m/s)

图15 无稳定板模型上表面平均流线和速度云图(风速10 m/s)Fig.15 Surface streamline and velocity cloud picture of tail of mode without central stabilizer(10 m/s)

图16 无稳定板模型尾部平均流线和速度云图(风速10 m/s)Fig.16 Surface streamline and velocity cloud picture of tail of mode without central stabilizer(10 m/s)
风速为10 m/s时有无中央稳定板两种工况之间流场的变化和风速为6 m/s时大致相同,只是当风速增大时,在中央稳定板下游侧形成的旋涡要稍微远离稳定板,这是由于较大的风速对旋涡的冲击作用更强所致。图14显示尾部流迹在模型尾部形成了一个体积较大的旋涡之后在该旋涡一定距离后再由一个体积更小的旋涡生成,两个旋涡的旋转方向一致。PIV试验的结果进一步验证了CFD数值模拟的正确性。
3结论
CFD数值模拟从细观的角度说明中央稳定板对桁架梁悬索桥断面绕流的作用机理。研究认为中央稳定板促进了在桥面中央附近形成位于上下桥面的旋涡对,使之相当于升力的作用,同时在无稳定板断面前端和尾部的旋涡体积减小,进而使桥梁断面在颤振中的竖向自由度参与作用增强,而非认为中央稳定板是切断了漩涡的传递路径,达到抑制旋涡移动的效果。
PIV流迹显示气流在中央稳定板的背风侧形成了漩涡,在模型尾部同样有旋涡的形成,这验证了CFD数值模拟的正确性,但PIV风洞试验发现在下游桥面栏杆附近有体积较小的旋涡形成,这是在CFD模拟中没有发现的。总的来说,两种细观机理研究表明中央稳定板使得在模型前后两段的旋涡体积减小,可能对模型的扭矩作用减弱;在上下中央稳定板背风侧形成的旋涡相当于升力作用,使得模型的竖向自由度参与增强,而扭转自由度的参与效应较弱。当然本文只进行了静场绕流的CFD数值模拟和PIV风洞试验,进一步的研究和试验对该结论的验证是必要的。
参 考 文 献
[1] Palombi E G, Kopp A, Gurka R. Particle image velocimetry measurements of wake flows of various bridge sections[C]// The fourth international symposium on computational wind engineering. Yokohama,2006:65-73.
[2] 张伟, 葛耀君. H形断面桥梁风致振动的流场机理[J]. 土木工程学报, 2009, 42(5): 90-95.
ZHANG Wei, GE Yao-jun.Flow-map mechanism of wind induced vibrations of H-shape bridge decks[J]. China Civil Engineering Journal, 2009, 42(5): 90-95.
[3] 张伟. 基于粒子图像测速技术的桥梁风致振动细观机理研究[D]. 上海: 同济大学, 2008:25-156.
[4] 刘祖军. 大跨桥梁颤振过程中的能量转化机理[D]. 上海: 同济大学,2011.
[5] Larsen A. Aerodynamics of the Tacoma Narrows Brigde-60 years later[J]. Journal of Structural Engineering International, 2000(10): 243-252.
[6] Watanabe S, Fumoto K. Aerodynamic study of slotted box girder using computational fluid dynamics[J]. Journal of Wind Engineering and Industrial Aerodynamics,2008(10/11): 1885-1894.
[7] Sarwar M W, Ishihara T. Numerical study on suppression of vortex-induced vibrations of box girder bridge section by aerodynamic countermeasures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(12):701-711.
[8] 陈政清,欧阳克俭,牛华伟,等. 中央稳定板提高桁架梁悬索桥颤振稳定性的气动机理[J]. 中国公路学报, 2009, 22(6): 53-59.
CHEN Zheng-qing, OUYANG Ke-jian, NIU Hua-wei,et al.Aerodynamic mechanism of improvement of flutter stability of truss-girder suspension bridge using central stabilizer[J]. China Journal of Highway and Transport, 2009, 22(6): 53-59.
[9] 欧阳克俭. 气动力有理函数与颤振稳定性的多因素分析[D].长沙: 湖南大学, 2011.
[10] 佟鼎, 黄宁.天然混合沙运动速度特征的风洞PIV实验[J]. 工程力学, 2011, 28(7): 229-237.
TONG Ding, HUANG Ning. Wind tunnel experiment of sand velocity in nature aeolian sand transport using particle image velocimetry [J]. Engineering Mechanics, 2011, 28(7): 229-237.
[11] 张伟, 葛耀君. 速度场演化结构非定常气动力[J]. 工程力学, 2009, 26(7): 229-237.
ZHANG Wei, GE Yao-jun.Evolution of unsteady aerodynamic forces for bodies from flow map[J]. Engineering Mechanics,2009, 26(7): 229-237.
[12] Wilde K, Fujino Y, Kawakami T. Analytical and experimental study on passive aerodynamic control of utter of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 80: 105-119.
[13] Matsumoto M, Yoshizumi F, Yabutani T, et al. Flutter stabilization and heaving-branch flutter[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999,83:42-56.
[14] 丁泉顺, 朱乐东. 主梁断面气动耦合颤振分析与颤振机理研究[J]. 土木工程学报, 2007, 40(3): 69-73.
DING Quan-shun, ZHU Le-dong.Aerodynamically coupling flutter analysis and flutter mechanism for bridge deck sections[J]. China Civil Engineering Journal, 2007, 40(3): 69-73.
基金项目:国家自然科学基金重大研究计划(重大建筑与桥梁强/台风灾变的集成研究91215303)
收稿日期:2014-05-22修改稿收到日期:2014-08-22
中图分类号:U441.3
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.01.003
Micro-mechanism of a central stabilizer for improving a bridge’s flutter stability
OUYANG Ke-jian1,2, CHEN Zheng-qing2
(1. State Grid Hunan Electric Power Corporation Research Institute, Changsha 410007, China;2. Wind Engineering Research Center, Hunan University, Changsha 410082, China)
Abstract:CFD numerical simulation and PIV wind tunnel tests were conducted to study the micro-mechanism of a central stabilizer for a flow around Aizhai truss suspension bridge cross-section. CFD numerical simulation showed that the central stabilizer promotes the formation of vortex pairs at the upper and lower deck near the center of the bridge deck and makes them be equivalent to the action of lift force; vortex volumes of front and tail of central stabilizer grow to enhance the participation function of the vertical DOFs of the bridge cross-section in flutter. PIV flow trace indicated that the air flow on the leeward side of the central stabilizer forms vortexes, the same vortex formation occurs at the end of the bridge model, the correctness of CFD numerical simulation is verified.
Key words:flutter; aerodynamic measures; central stabilizer; PIV; CFD
第一作者 欧阳克俭 男,博士,高级工程师,1981年生
