基于电压源换流器的三端直流输电系统的研究
2016-07-25郭启伟刘玉海刘丙伟任庆帅田智勇常高颂胡姿屹
郭启伟,刘玉海,刘丙伟,任庆帅,田智勇,常高颂,胡姿屹
(国网山东省电力公司检修公司,山东 济南 250118)
基于电压源换流器的三端直流输电系统的研究
郭启伟,刘玉海,刘丙伟,任庆帅,田智勇,常高颂,胡姿屹
(国网山东省电力公司检修公司,山东济南250118)
〔摘 要〕介绍了基于电压源换流器的三端直流输电系统的直流线路拓扑结构,推导了采用环形拓扑结构的三端直流输电系统在不同稳态运行工况下主导换流站有功潮流和各换流站直流电压的计算公式,并分析了调度中心在三端直流输电控制系统中的作用,最后仿真验证了在不同运行状况下三端直流输电系统的有功潮流和电压计算公式的准确性和可靠性。
〔关键词〕直流输电;电压源换流器;三端直流;拓扑结构
0 引言
基于电压源换流器的高压直流输电(VSCHVDC)不同于传统的直流输电,在改变潮流方向时不仅能够保持直流电压极性不变,而且能够控制交流潮流和提供动态无功补偿。这种特点使得基于电压源换流器的多端直流输电(VSC-MTDC)适用于分布式发电并网、为大城市的多处负荷中心供电等中小功率应用领域。
当VSC-HVDC系统用于联结3个有源电网、2个分布式电源并网或向大城市的2个负荷中心供电等时,可以采用基于电压源换流器的三端直流输电(VSC-TTDC)系统。另外,从经济性和实用性的角度考虑,VSC-MTDC系统可以基于原有的双端VSC-HVDC系统进行分期扩建。因此,要建成一个具有多端换流站的直流输电系统,首先需要建立一个可长期稳定运行的三端直流输电系统,这是一种实用、经济的方案。
为了维持VSC-TTDC系统的有功功率平衡和直流电压稳定,必须有一端换流站采用定直流电压控制。当该换流站的交流侧电网发生故障时,电网电压跌落将导致其进入限流模式而失去直流电压控制。若换流站间没有通信或通信存在一定的延时,其他换流站将保持有功功率传输不变,向直流线路注入或汲取有功功率,导致直流电压上升或下降,威胁直流系统的安全稳定运行。为了抑制这种暂态过电压/欠电压,需要进行故障控制策略的设计。故障的判断一般采用基于本地的直流电压信号,其优点是可靠且不需要远程实时通信。为选取控制保护策略的各直流电压指令值和阈值,需要对各种稳态运行情况下的VSC-TTDC系统各换流站直流电压和主导换流站有功潮流进行求解,以便为指令值的选取提供可靠的基准值。
1 VSC-TTDC系统的拓扑结构
VSC-TTDC系统的典型拓扑结构可以分为环形和星形2种,分别如图1(a)和1(b)所示。无论采用哪种结构,必须有一个换流站作为主导换流站,用于VSC-TTDC系统的直流电压控制。
1.1环形拓扑结构分析
环形拓扑结构的优点如下。
(1)系统可靠性高。对每个换流站均有2条直流线路与其相连,即采用双端供电方式,且当其中任意一条线路停运时仍能保证所有换流站的正常并网运行。
(2)系统运行方式灵活。可通过直流线路开关的开合,组成不同的拓扑结构,以满足不同应用场合的需求。
(3)直流线路检修方便。当对某一线路进行检修时,不会影响到各换流站的正常并网运行。
环形拓扑结构的缺点如下。
(1)直流线路建设投资较大。
(2)环形结构使得换流站直流侧电压的计算变得复杂,不利于基于本地直流电压信号控制策略指令值的整定。
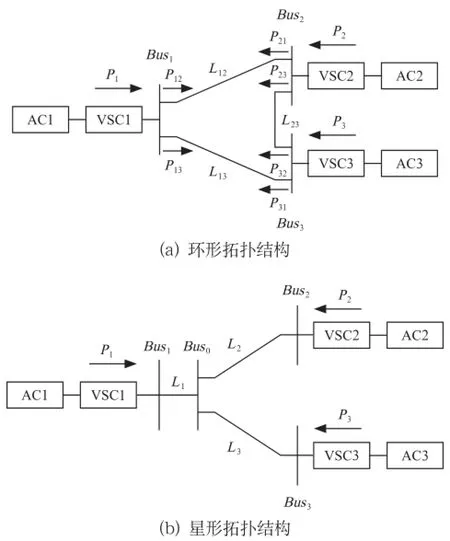
图1 VSC-TTDC系统的直流拓扑结构
1.2星形拓扑结构分析
星形拓扑结构的优点如下。
(1)直流线路的建设投资比环形拓扑结构的要少,尤其是当一侧换流站与其他换流站距离较远时。
(2)换流站直流侧电压的计算均与双端直流输电系统类似,便于基于本地直流电压信号控制策略指令值的整定。
星形拓扑结构的主要缺点是系统可靠性差。任意1条线路退出都将导致至少1个换流站停运,尤其是当定直流电压控制换流站所连接的线路故障停运时,若不采取相应的控制措施维持系统直流侧电压稳定,将导致整个VSC-TTDC系统停运,属于极严重的故障。
由于可靠性是VSC-TTDC系统正常运行的关键之一,故环形拓扑结构将比星形拓扑结构具有更大的优势和更广阔的应用空间。以下将环形拓扑结构作为研究对象,讨论VSC-TTDC系统在不同稳态运行工况下的直流电压计算方法。
2 换流站直流电压和有功潮流的计算方法
换流站VSC1,VSC2和VSC3一般均采用2电平结构和分裂电容中点接地,换流站直流侧电压分别为Udc1,Udc2和Udc3,流入换流站的交流有功功率分别为P1,P2和P3。由于是针对稳态运行情况进行计算,故直流线路模型可以采用电阻型集中参数等值电路表示,单位长度直流线路的电阻值为R,线路长度如图1(a)所示。为方便分析,令图1(a)中的换流站VSC1作为定直流电压控制换流站,其容量足够大且忽略纹波影响,即换流站VSC1的直流侧电压维持为Udc1恒定;VSC2和VSC3采用定有功功率控制方式,且为无差调节。
研究中,已知量包括指令参考值Udc1,P2和P3,线路参数L12,L13,L23和R,以及换流站损耗率λ;未知量包括P1,Udc2和Udc3。直流线路的有功潮流可由上述量进行表述,假定所有工况均为稳定运行状态,可忽略谐波分量的作用。
2.1正常运行时
当线路正常运行时,根据节点处的有功潮流平衡可得:
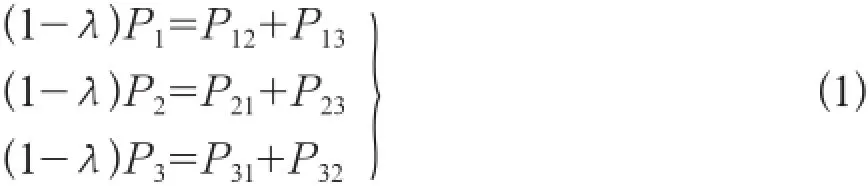
其中,λ为换流站损耗率,即换流站的交流并网点母线到直流母线的有功功率损耗与交流并网点有功功率的比率;Pij(i,j=1,2,3)为从直流母线i处流向直流母线j的直流功率,即直流线路Lij功率,其计算公式为:
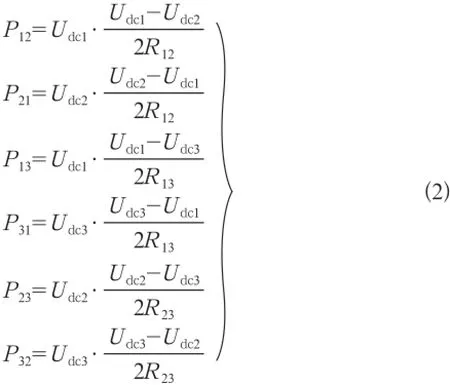
其中,R12=L12R,R13=L13R,R23=L23R。
将式(2)代入式(1)可得到三元二次方程组:

其中,Udc1,P2和P3可以直接取换流站的指令参考值,为已知量。P1,Udc2和Udc3为未知量。将各换流站直流电压值代入式(2)即可得到直流线路的有功功率。式(3)的求解可借助MATLAB软件的solve函数。
另外,为获得式(3)的真解,需要附加条件:
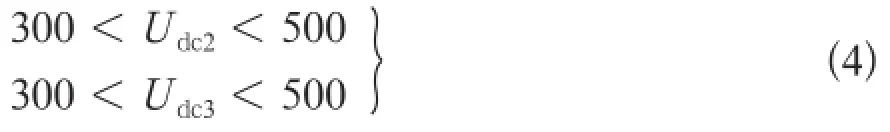
对式(3)求解时,可能没有实数范围内的真解。若某一组解的虚部趋向于无穷小,且实部满足式(4),则认为解的实部是符合要求的方程组真解。
2.2线路L23停运时
当线路L23停运时,以主导换流站作为中心节点,则VSC-TTDC系统的主电路结构变为星形结构。此时,P23和P32均为0,则由式(1)和式(2)可得:
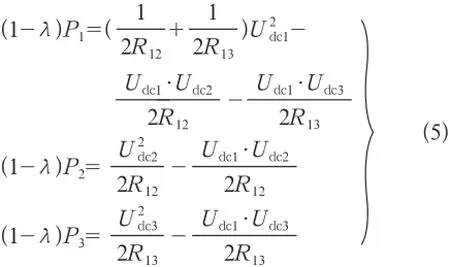
式(5)的求解过程类似式(3)。
2.3线路L12或L13停运时
线路L12或L13停运时的2种情况类似。以线路L13停运时为例,以主导换流站为首端节点,则VSC-TTDC系统的主电路结构变为链状结构。此时P13和P31均为0,则由式(1)和式(2)可得:
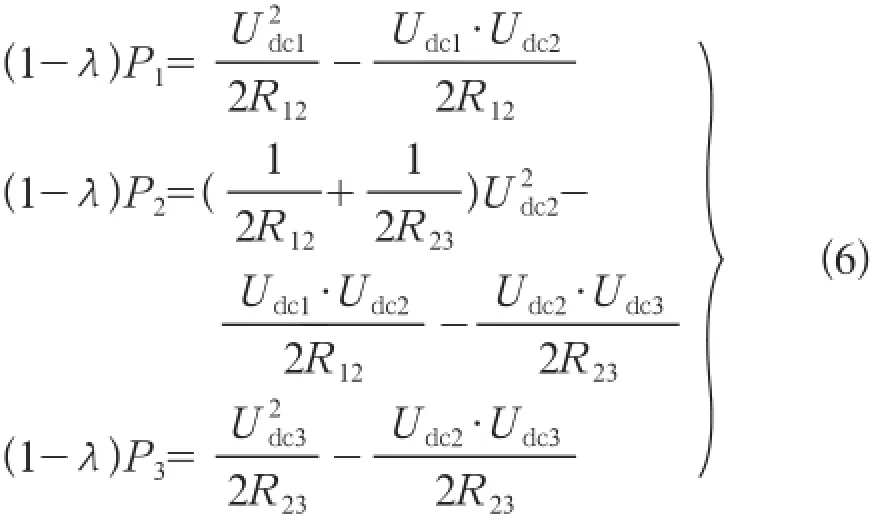
式(6)的求解过程类似式(3)。
2.4当某一换流站停运时
当换流站VSC1停运时,VSC-TTDC系统将失去直流电压控制的能力,此时需要设计相应的控制策略来维持系统的直流电压。由于本研究未考虑主导换流站停运时的控制策略,故认为当主导换流站退出时整个VSC-TTDC系统退出运行。
当换流站VSC2或VSC3停运时,剩余系统均相当于双端VSC-HVDC系统。以VSC3停运为例,此时线路L13和L23均停运,故P13,P31,P23和P32均为0,要求解的未知量为P1和Udc2,则由式(1)和式(2)可得:

式(7)的求解过程类似式(3)。
3 调度中心的作用
调度中心负责指定主导换流站,即指定某一换流站的有功类控制器为定直流电压控制器,并向各换流站发出控制模式选择指令和负责指令参考值的下发。同时,调度中心能够实时监控VSC-TTDC系统的运行工况。因此,调度中心可根据线路参数、实时的指令参考值和系统的运行工况,结合上述公式对各换流站直流电压和主导换流站有功潮流进行计算,并将计算结果实时地下发到各换流站,以便整定各换流站的控制保护策略等。
4 仿真验证
为了验证各换流站直流电压和主导换流站有功潮流计算公式的准确性,在PSCAD/EMTDC环境中建立了如图1(a)所示的VSC-TTDC系统仿真模型。所有换流站均采用相同的电路结构,单个换流站的详细电气接线如图2所示,直流线路的集中参数模型如图3所示,仿真模型的参数选择如表1所示,换流站损耗率λ取值为2%。

图2 换流站的电气接线

图3 直流线路的集中参数模型
4.1计算与仿真结果比较
根据以上推导公式,分别求解在正常运行、线路L23停运、线路L13停运和换流站VSC3停运4种运行工况,不同指令参考值条件下的各换流站直流电压和主导换流站有功潮流,求解结果如表2所示。利用PSCAD建立VSC-TTDC系统的详细模型,进行时域数字仿真,对上述各种工况下各换流站直流电压主导换流站有功潮流和进行验证,得到仿真结果的平均值如表2所示。
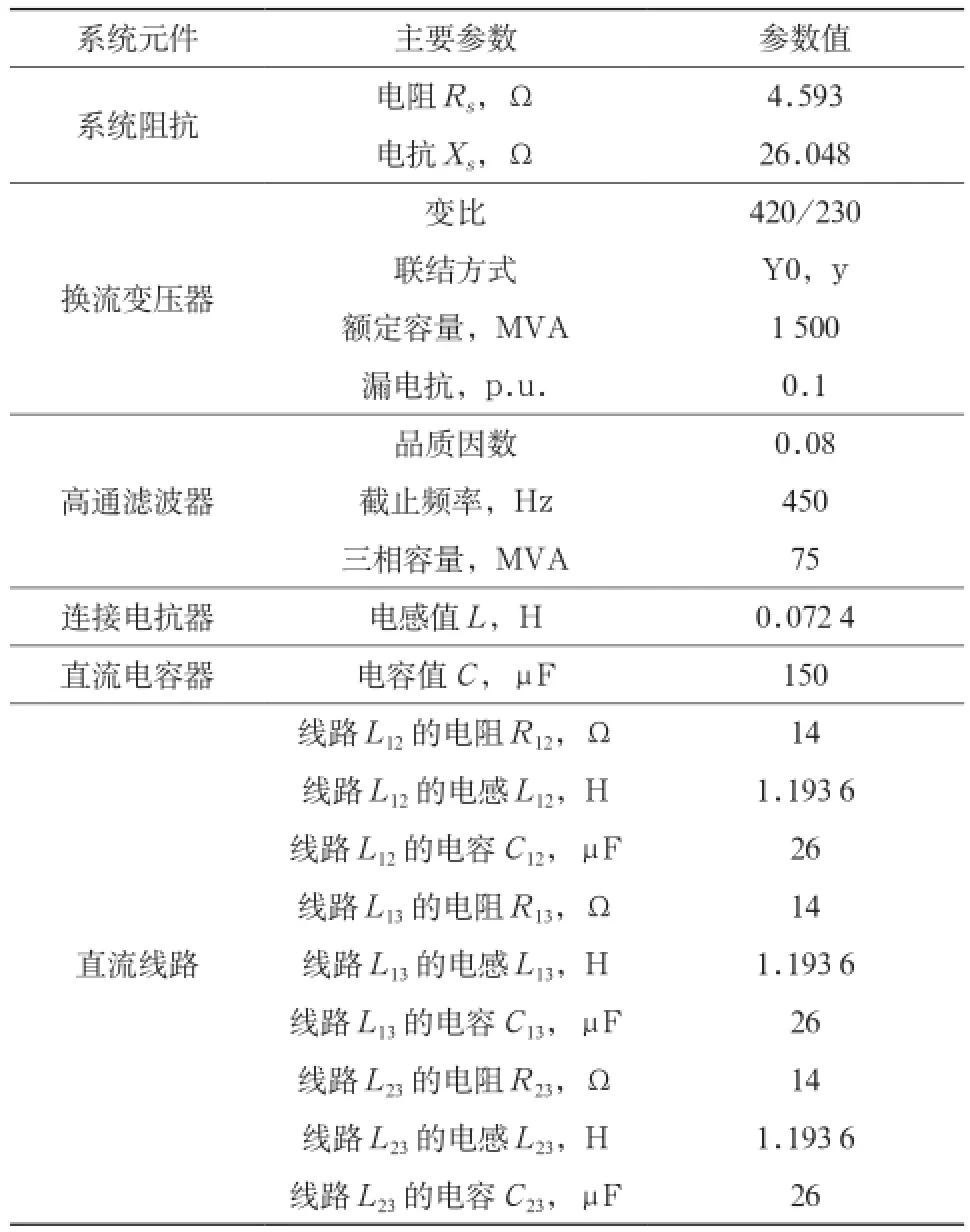
表1 仿真模型参数
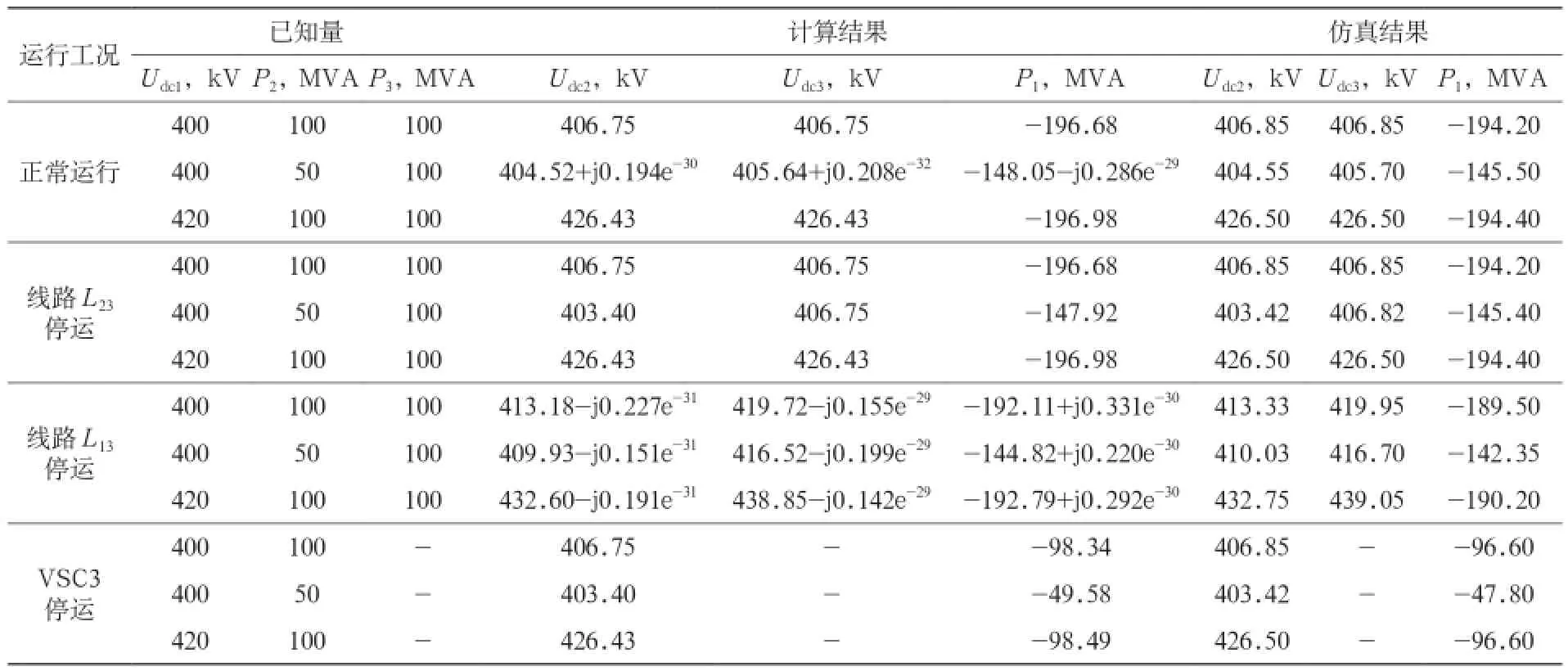
表2 计算与仿真结果比较
由表2可知,在正常运行和线路L13停运2种运行工况下,部分计算结果为复数,其虚部均接近于无穷小。通过与仿真结果的比较可知,这些复数值的实部全部能够与仿真结果相吻合,故取其实部作为非线性方程组的解能够满足计算的需要。
通过比较4种运行工况下的计算结果与仿真结果可知,换流站VSC2,VSC3直流电压Udc2,Udc3的计算结果在所有运行工况下都非常接近仿真结果,误差范围在(-0.05)-0kV。因此,该计算结果能够为控制保护策略的设计提供一个可靠的基准。主导换流站的交流侧有功功率P1的计算结果比较接近仿真结果,偏差范围一般为(-3)-(-1)MW。
由正常运行和直流线路L23停运2种运行工况下的计算和仿真结果可知:当换流站VSC2和VSC3的有功功率指令值相等时,Udc2=Udc3,线路L23上没有潮流流过,此时正常运行与线路L23停运2种运行工况下的有功潮流与直流电压均相同。对于正常情况下来说,当P2=P3时,直流线路L23并没有得到充分的利用,成为没有功率流动的联络线,仅用于保证两端换流站供电的可靠性。
当直流线路L23停运时,VSC-TTDC系统成为星形结构,且主导换流站VSC1作为中心节点。当换流站VSC3停运时,VSC-TTDC系统成为一个双端VSC-HVDC系统。通过比较直流线路L23和换流站VSC3停运2种运行工况发现,在星形结构中,各换流站的直流电压仅与本站的有功功率指令值密切相关,与其他换流站的指令值无关,且与双端VSC-HVDC系统的计算结果相同。即线路L23停运时VSC-TTDC系统相当于2个独立运行的双端VSC-HVDC系统。
当直流线路L13停运时,VSC-TTDC系统成为链状结构,且主导换流站VSC1作为首端节点。由表2计算结果和仿真结果可知,当所有换流站的有功功率指令值均为正时,即各换流站均流入有功功率,末端换流站直流侧的电压将随着换流站数量的增加而提高,从而导致末端换流站的直流电压偏高,这将不利于系统直流侧电压的控制。
4.2计算误差来源
在进行各换流站直流电压和主导换流站有功潮流计算时,误差的主要来源包括以下几个方面。
(1)换流站损耗率λ是一个变量,由多种因素所决定,主要取决于交直流电压等级和换流站的交流侧有功功率。而计算中λ取固定值会带来一定的误差,这是计算的主要误差来源。
(2)计算是在忽略连接电抗器和直流侧电容器等储能元件动态特性的基础上进行的,并且得到的计算结果是固定值。实际上,PSCAD的时域仿真考虑到了储能元件的影响,并且仿真结果存在固定频率的、小幅度的波动。
(3)计算与仿真所采用的直流线路模型不同,为简化计算过程,所采用的直流线路模型为集中电阻,PSCAD仿真采用的为集中π型等效电路,考虑到了线路电感和电容的作用。
(4)求解非线性方程组过程中由于虚数解的存在,取虚部接近于无穷小的解的实部作为符合要求的解会带来一定的误差。
5 结束语
(1)本文推导出的计算公式能够准确地计算出VSC-TTDC系统在正常运行情况、1条直流线路停运和某一换流站停运情况下的各换流站直流电压和主导换流站有功潮流。
(2)计算误差来源主要包括换流站损耗率、动态储能元件、直流线路模型和虚数解处理的影响,误差均在合理的范围内。
参考文献:
1 Flourentzou N,Agelidis V G, Demetriades G D. VSC-Based HVDC power transmission systems: An Overview [J].IEEE Trans. on Power Electronics,2009,24(3):592-602.
2 李庚银,吕鹏飞,李广凯,等.轻型高压直流输电技术的发展与展望[J].电力系统自动化,2007,27(4):77-81.
3 徐政,陈海荣.电压源换流器型直流输电技术综述[J].高电压技术,2007,33(1):1-10.
4 胡兆庆,毛承雄,陆继明,等.一种新型的直流输电技术——HVDC Light[J].电工技术学报,2005,20(7):12-16.
5 朱晓东,周克亮,程明,等.大规模近海风电场VSC-HVDC并网拓扑及其控制[J].电网技术,2009,33(18):17-24.
6 Tang Liangxiang and Ooi Boon-Teck. Locatingand Isolating DC Faults in Multi-Terminal DC Systems[J].IEEE Transactions on Power Delivery,2007,22(3):1877-1884.
7 Lu Weixing and Ooi Boon-Teck.DC Overvoltage Control During Loss of Converter in Multi-terminal Voltage-Source Converter-Based HVDC[J].IEEE Transactions on Power Delivery,2003,18(3):915-920.
8 Jin Yang, Fletcher E John and O’Reilly.Multiterminal DC Wind Farm Collection Grid Internal Fault Analysis and Protection Design[J].IEEE Transactions on Power Delivery,2010,25(4):2308-2318.
9 陈海荣,徐政.适用于VSC-MTDC系统的直流电压控制策略[J].电力系统自动化,2009,33(12):57-60.
10 阮思烨,李国杰,孙元章.多端电压源型直流输电系统的控制策略[J].电力系统自动化,2009,33(12):57-60.
11 吴俊宏,艾芊,章健,等.基于多代理技术的VSCMTDC控制系统[J].电力系统自动化,2009,33(19):85-89.
12 赵成勇,胡东良,李广凯,等.多端VSC-HVDC用于风电场联网时的控制策略[J].电网技术,2009,33(17):135-140.
13 李胜.柔性直流技术在城市电网中应用研究[D].北京:华北电力大学,2009.
14 张静,徐政,潘武略.VSC-HVDC系统新型广义直流电压控制策略[J].电力系统自动化,2008, 32(21):46-50.
15 张静,徐政,王峰.包含VDCCOL的VSCHVDC改进控制策略[J].电力系统自动化,2008,32(22):41-46.
16 丁涛,张承学,孙元博.基于本地信号的VSC-MTDC输电系统控制策略[J].电力系统自动化,2010,34(9):44-48.
17 张志涌.精通Matlab 6.5版教程[M].北京:北京航天航空大学出版社,2003.
收稿日期:2015-10-13。
作者简介:
郭启伟(1985-),男,工程师,主要研究方向为电力系统继电保护技术,email:276964876@qq.com。
刘玉海(1982-),男,工程师,主要研究方向为电力系统变电运维管理。
刘丙伟(1971-),男,工程师,主要研究方向为电力系统变电安全管理。
任庆帅(1980-),男,工程师,主要研究方向为电力系统变电检修管理。
田智勇(1981-),男,工程师,主要研究方向为电力系统变电运维管理。
常高颂(1990-),男,助理工程师,主要研究方向为电力系统继电保护技术。
胡姿屹(1991-),女,助理工程师,主要研究方向为电力系统继电保护技术。
