余弦高斯光束通过负折射率介质的传输特性
2016-07-25许森东
许森东
(浙江科技学院 理学院,杭州 310023)
余弦高斯光束通过负折射率介质的传输特性
许森东
(浙江科技学院 理学院,杭州 310023)
摘要:在傍轴近似情况下,利用柯林斯公式计算出了余弦高斯光束通过负折射率介质的光强解析表达式。研究了负折射率材料工作频率和余弦高斯光束的调制参数对余弦高斯光束光强的影响。计算结果表明:可以利用负折射率介质的工作频率控制余弦高斯光束的光强。此研究结果提供了一种控制余弦高斯光束传输特性的新方法和技术。
关键词:柯林斯公式;余弦高斯光束;负折射率介质;光强
余弦高斯光束作为厄米正弦类高斯光束的一种特例[1],它能够更好地描述带有相位台阶光学谐振腔的光束模型。由于余弦高斯光束在实际工作中的潜在应用价值,因而受到相关研究人员的重视,并进行了大量研究。王喜庆等研究了在自由空间中无光阑情况下余弦高斯光束的传输和通过薄透镜的传输特性[2];李艳桃等研究了余弦高斯光束在单轴晶体中垂直于光轴的传输特性[3];宋宏远等研究了余弦高斯光束在梯度折射率介质中的传输特性[4];姜向东等研究了余弦高斯光束的焦平面及其位置,得到了束腰宽度和位置, 并进一步给出了余弦高斯光束的相对焦移计算公式[5]。
另外,负折射率材料也是当前十分活跃的研究领域,负折射率材料具有负磁导率、负介电常数及负折射率;利用负折射率材料可实现完美透镜等[6]。科研人员在负折射率介质的研究中最开始在微波波长范围内实现了负折射率,随着技术的发展,目前已经有很多科研机构获得了可见光波长范围的负折射率,如中国科学院长春光学精密机械与物理研究所利用溶致液晶模板成功制备了可见光负折射材料。负折射率材料具有超常且独特的光学特性,因此,研究余弦高斯光束在负折射率介质中的传输是一项很有意义的工作。
本研究从余弦高斯光束的基本原理出发,研究余弦高斯光束在负折射率介质中的传输与调控。利用Collins公式计算得到余弦高斯光束通过NIM(negative index medium, 负折射率介质)的光强分布函数表达式,并且利用该式研究余弦高斯光束的调制参数和NIM的工作频率对光强的影响。
1负折射率介质
研究Drude模型的NIM,该模型NIM的等效磁导率μeff为[7]:

(1)
式(1)中: ωmp为磁场等离子体的圆频率;ωmo为构成NIM中金属环的谐振圆频率;ω为该NIM的工作圆频率;γ为NIM的损耗特征参数。
等效介电常数εeff为:

(2)
式(2)中,ωep为电子的等离子圆频率, ωeo为电子的谐振圆频率。
NIM的折射率可表示为:

(3)
2余弦高斯光束通过NIM的传输特性
在傍轴近似情况下,余弦高斯光束沿z轴进入NIM。 在z=0初始平面上,余弦高斯光束的场分布为[8]:
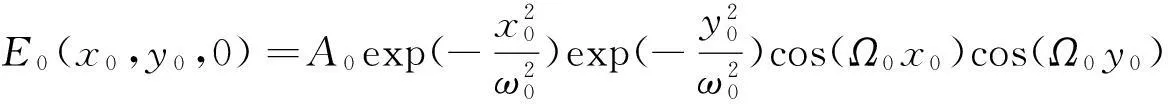
(4)
式(4)中:ω0为余弦高斯光束的束腰宽度;Ω0为余弦高斯光束余弦项相关参数值;A0为场中心处的振幅。
在傍轴传输情况下,利用柯林斯衍射积分公式可得,当余弦高斯光束通过NIM后,输出平面的场分布可以表示为:
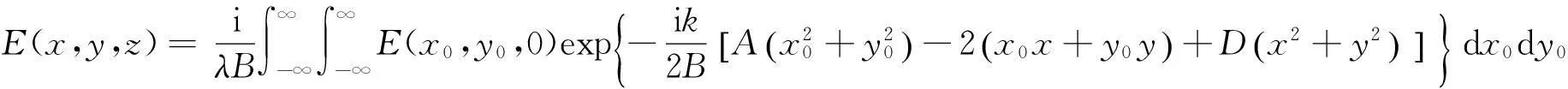
(5)
式(5)中:k为波数;A、B和D为该光学系统的传输矩阵元。余弦高斯光束通过NIM的传输矩阵可表示为:

(6)
利用积分式

将式(4)代入式(5),经积分整理后得到:

(7)

(8)
此时,余弦高斯光束的光强I为:
I(x′,y′,z)=E(x′,y′,z)E*(x′,y′,z)。
(9)
将式(8)代入式(9)即可得到余弦高斯光束的光强:


(10)
当x′=y′=0时,可以得到余弦高斯光束在NIM中沿轴向的光强分布:

(11)
式(11)显示,可以通过调控负NIM的折射率来控制余弦高斯光束的光强,改变NIM的z值也可以控制余弦高斯光束的光强。从式(1)、式(2)和式(3)可以看出:NIM的折射率可以通过工作频率调控,因此,调控NIM的工作频率即可实现对余弦高斯光束光强的控制。
3计算结果与分析


图1 NIM工作频率f分别为12.2、12.3、12.4、12.5 GHz时轴上光强随z的变化Fig.1 Light intensity changing with propagation distance when NIM frequencies are 12.2,12.3,12.4 and 12.5 GHz
图1为调制参数α=1.5,NIM工作频率f分别为12.2、12.3、12.4、12.5GHz时余弦高斯光束通过NIM轴上光强随z的变化图。从图中可以看出,光强在z=0时最大且最大值不随NIM的工作频率变化;光强随z的增加而逐渐减小,光强趋于0但大于0。当z相同而NIM的工作频率不同时,光强也具有不同值;其原因为NIM的折射率随工作频率变化而变化。
图2为NIM的工作频率f=12.2GHz,调制参数α分别为1.5、2.0、2.5、3.0时余弦高斯光束通过负折射率介质轴上光强随z的变化图。从图中可以看出,光强在z=0时最大;光强随z的增加而逐渐减小。当调制参数不同时,光强也具有不同值,且同一z值时调制参数越大光强越小;其原因是随着调制参数α增大,光强越来越小。
图3为在调制参数α分别为1.5、2.0、2.5、3.0时输出平面余弦高斯光束的光强随NIM的工作频率变化图,取z=30 mm,NIM的工作频率从12.1 GHz到12.8 GHz,结果显示余弦高斯光束强度随NIM的工作频率增加而逐渐减小。在NIM的工作频率为12.1 GHz时,不同调制参数的光束光强基本相同,但随着工作频率的增加,由于变化率不同而逐渐区分开,随后又逐渐趋于同一值。此结果表明,可以通过调控NIM的工作频率来控制余弦高斯光束的光强。

图2 调制参数α取1.5、2.0、2.5、3.0时轴上光强随z的变化Fig.2 Light intensity changing with propagation distance when modulation parameters are 1.5,2.0,2.5 and 3.0

图3 调制参数α取1.5、2.0、2.5、3.0时轴上光强随工作频率的变化Fig.3 Light intensity changing with frequency when modulation parameters are 1.5,2.0,2.5 and 3.0
4结语
通过分析得到了余弦高斯光束通过NIM的输出平面光强的解析表达式。该解析表达式可用于计算和研究余弦高斯光束通过NIM的光强。研究发现,余弦高斯光束的光强可以通过NIM的工作频率来调控。研究结果提供了一种控制余弦高斯光束传输特性的新方法和技术;调控NIM的工作频率,就可以控制余弦高斯光束的光强。该研究成果对利用NIM实现光学操控具有潜在的应用价值。
参考文献:
[1]王绍民,林强,江晓清.余弦-高斯光束[J].光子学报,1999,28(4):368.
[2]王喜庆,柯尊平,吕百达.余弦高斯光束的传输特性[J]. 激光技术,2001,25(2):122.
[3]李艳桃,张廷蓉,张伟林,等.余弦高斯光束在单轴晶体中垂直于光轴的传输[J].四川师范大学学报(自然科学版),2013,36(6):893.
[4]宋宏远,张廷蓉,陈森会,等.余弦-高斯光束在梯度折射率介质中的传输特性[J].强激光与粒子束,2011,23(4):890.
[5]姜向东,吴运梅,王喜庆.余弦-高斯光束的焦平面及其位置[J].光学技术,2006,32(3):419.
[6]庄飞,沈建其.双轴各向异性负折射率材料光纤中光子波函数几何相位研究[J].物理学报,2005,54(2):955.
[7]SHELBY R A, SMITH D R, SCHULTZ S. Experimental verification of a negative index of refraction [J]. Science, 2001,292(5514):78.
[8]许森东.余弦高斯光束通过EIT介质的传输特性研究[J].浙江科技学院学报,2014,26(1): 6.
doi:10.3969/j.issn.1671-8798.2016.03.002
收稿日期:2016-04-13
基金项目:浙江省教育厅科研计划项目(Y201533236)
作者简介:许森东(1981—),男,重庆市大足人,高级实验师,硕士,主要从事人工复合电磁介质研究。
中图分类号:O431.2
文献标志码:A
文章编号:1671-8798(2016)03-0182-04
Study on propagation properties of cosine-Gaussian beams through negative index medium
XU Sendong
(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)
Abstract:Under condition of paraxial approximation, the analytical expression is obtained for the intensity function of a cosine-Gaussian beam passing through negative index medium based on the Collins’ formula. The influence of intensity of cosine-Gaussian beams due to negative index medium’s frequency and cosine-Gaussian beams’ modulation parameter are analyzed. Numerical examples show that the intensity of cosine-Gaussian beams can be modulated by the frequency of negative index medium. The results provide a new method and technique for controlling the beam intensity.
Keywords:Collins’ formula; cosine-Gaussian beams; negative index medium; intensity
