广义零差分平衡函数的一个注记
2016-07-24廖群英
蒋 林,廖群英
(四川师范大学数学与软件科学学院,四川成都610066)
广义零差分平衡函数的一个注记
蒋 林,廖群英*
(四川师范大学数学与软件科学学院,四川成都610066)
将零差分平衡函数的定义推广到广义零差分平衡函数(G-ZDB),并利用p分圆陪集构造一类新的广义零差分平衡函数,其中p为质数.
零差分平衡函数;广义零差分平衡函数;p分圆陪集
1 预备知识及主要结果
设(A,+)和(B,+)均为交换群,且|A|=n,|B|=l.映射f:A→B称为广义零差分平衡函数(G-ZDB),是指存在非空集合,使得对任意0≠ a∈A,均有

特别地,当S是单元集时,f是零差分平衡(ZDB)函数,简记为(n,λ)-ZDB函数[1].

包含了A中所有非零元素的λ倍,则称P为(n,{t0,t1,…,t珋l-1},λ)-差分集(PDF).基于零差分平衡函数与PDF的联系,零差分平衡函数可记为(n,{t0,t1,…,t珋l-1},λ)-ZDB函数.有时不用考虑参数{t0,t1,…,t珋l-1},简记为-ZDB函数,此时广义零差分平衡函数简记为函数.
零差分平衡函数常常应用于组合学、代数学、有限几何以及编码和密码学等领域,它是 C.S.Ding[1-2]在构造最佳常组合码与优化及完善差分系统中引入的.熟知,完美非线性函数和差分函数均是特殊的零差分平衡函数[3-7].基于其良好的特性,人们可构造出最佳组成权重码和最优跳频序列[7-9].事实上,人们已经构造出大量的ZDB函数[1-2,7,10-11].特别地,C.S.Ding等[11]用2分圆陪集构造了参数为

的零差分平衡函数,其中m为素数.本文将零差分平衡函数推广到广义的零差分平衡函数,并利用p分圆陪集在模n=p2q-1(p,q为不同奇素数)上的性质,构造了一类广义零差分平衡函数.
定义1.1[11]令n=pm-1,其中m∈N+,则对任意的i∈{0,1,…,n-1},模n的含i的p分圆陪集定义为

其中 li是使得 i≡i×pli(mod n)成立的最小正整数.
同时,定义Ai中最小的正整数为Ai的首位.当i≠0时,Ai称为非零p分圆陪集.
定理1.2[11]设p、q为奇素数,n=p2q-1,Ai为模n的含i的p分圆陪集,M为模n的全部非零p分圆陪集的个数,则对任意的i∈{1,2,…,n-1},|Ai|∈{1,2,q,2q}且


定理1.3 设p,q为不同的奇素数,n=p2q-1,则存在参数为

的G-ZDB函数,其中

2 主要结果的证明
引理2.1[12]设a,n1,n2∈Z+,n1≠n2,则
3)除此之外,


有解的充分必要条件是gcd(m1,m2)| b1-b2.进而在有解时,其关于模lcm[m1,m2]恰有唯一解.
定理 1.2的证明 由 n=p2q-1知 p2q≡1(mod n),即|Ai|≤2q.又由i≡i×pli(mod p2q-1)知(p2q-1)| i×(pli-1).由引理2.1知gcd(p2q-1,pli-1)=pgcd(2q,li)-1.注意到q为奇素数,故
引理2.2[12]设m1、m2是2个正整数,b1、b2为整数,则同余式组


所以对模n的任意非零p分圆陪集Ai,有|Ai|=li∈{1,2,q,2q},且模n的全部非零p分圆陪集的个数为
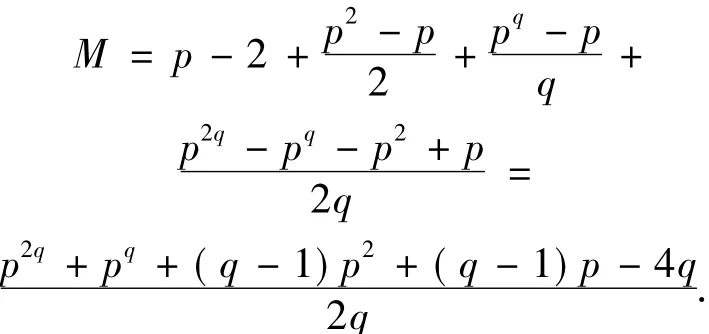
定理1.3的证明 令T表示模n=p2q-1的所有p分圆陪集首位的集合,则由定理1.2可知

现定义f:Zn→Zn为

其中ix为x所在的p分圆陪集的首位,则

另一方面,对任意的a∈{1,2,…,p2q-2},若存在x∈Zn,使得f(x+a)=f(x),则存在1≤k≤2q-1(k∈N),使得

即
同余(1)式有解当且仅当 g cd(p2q-1,pk-1)= (pgcd(2q,k)-1)| a,且有解时,恰有 pgcd(2q,k)-1个解,因此有以下4种情形.
情形1 (p2-1)| a且(pq-1)| a.
(A) gcd(2q,k)=1时,同余(1)式恰有p-1个解,且

故解集为

又满足gcd(2q,k)=1的k恰有φ(2q)=q-1个,故此时

(B) gcd(2q,k)=2时,同余(1)式恰有p2-1个解,且

故解集为

又满足gcd(2q,k)=2的k恰有q-1个,故此时

(C) gcd(2q,k)=q时,同余(1)式恰有pq-1个解,且

故解集为

又满足gcd(2q,k)=q的k只有1个,即k=q,故此时

因此当A11、A12、A13两两无交时,由(3)、(5)及(7)式知:对任意满足(p2-1)| a且(pq-1)| a的a,均有

下面讨论A11、A12、A13两两相交的情形.

注意到gcd(2q,k2)=2,故(p2-1)|(pk2-1),从而有

即

令d1=gcd(2q,|k1-k2|),由 q为奇素数以及gcd(2q,k1)=1,gcd(2q,k2)=2知d1∈{1,q}.
1)若d1=1,则由(9)式可知

而

因此

注意到q为奇素数,于是

(a)n1=p+1时,则由(p2-1)| a及(10)和 (11)式知,此与a∈{1,2,…,p2q-2}矛盾,故
(b)n1=(p+1)q时,由(p2-1)| a及(10)和(11)式知.又gcd(pq+1,pq-1)=2且,故

又(pq-1)| a,故a,此与a∈{1,2,…,p2q-2}矛盾,故
2)若d1=q,则由(9)式可知.又由假设条件以及gcd(pq-1,pq+1)= 2可知a.注意到


从而有

即

令d2=gcd(2q,|k1-q|),由 q为奇素数以及gcd(2q,k1)=1知d2=2.于是由(12)式知

又

则

注意到q为奇素数且gcd(p+1,p-1)=2,故有以下3种情形.
(a)gcd(q,p2-1)=1时,即n2=1,由(p2-1) | a知,此与a知.由费马小定理知pq≡p(mod q),故pq-1≡p-1≡0(mod q),pq+ 1≡p+1(mod q),所以∈{1,2,…,p2q-2}矛盾,故A11∩A13=Ø.

(b)q|(p-1)时,即n2=q,由(p2-1)| a

注意到(pq-1)| a,故1)| a,此与a∈{1,2,…,p2q-2}矛盾,故A∩A
1113
(c)q|(p+1)时,即n2=q,由(p2-1)| a知.由费马小定理知pq≡p(mod q),故pq+1≡0(mod q),所以

注意到(pq-1)| a,故| a,即q|(p+1)且,此时同余(2)和 (6)式关于模有唯一解,设为,故

又|A11|=p-1,故A11⊆A13,此时


从而

于是

令d3=gcd(2q,|k2-q|),由 q为奇素数以及gcd(2q,k2)=2知d3=1.类似于情形(Ⅰ)的d1=1的证明可推出矛盾,于是
情形2 (p2-1)| a且时.
(A)gcd(2q,k)=1时,同余(1)式恰有p-1个解,且

故解集为

又满足gcd(2q,k)=1的k恰有φ(2q)=q-1个,故此时

(B)gcd(2q,k)=2时,同余(1)式恰有p2-1个解,且

故解集为

又满足gcd(2q,k)=2的k恰有q-1个,故此时

(C)gcd(2q,k)=q时,同余(1)式无解,此时



注意到gcd(2q,k2)=2,故(p2-1)|(pk2-1),从而有

于是

令d4=gcd(2q,|k1-k2|),由 q为奇素数以及gcd(2q,k1)=1,gcd(2q,k2)=2知d4∈{1,q}.
1)若d4=1,则由(20)式可知


(a)n1=p+1时,则由(p2-1)| a知,此与a∈{1,2,…,p2q-2}矛盾,故
(b)n1=(p+1)q时,则由(p2-1)| a知




又|A21|=p-1,故A21⊆A22.

综上,由(19)和(21)式知:对于任意满足(p2-1) | a且的a,均有

(A)gcd(2q,k)=1时,同余(1)式恰有p-1个解,且

故解集为

又满足gcd(2q,k)=1的k恰有φ(2q)=q-1个,故此时

(B)gcd(2q,k)=2时,同余(1)式无解,此时

(C)gcd(2q,k)=q时,同余(1)式恰有pq-1个解,且

故解集为

又满足gcd(2q,k)=q的k只有1个,即k=q,故此时



从而

于是

令d5=gcd(2q,|k1-q|),由 q为奇素数以及gcd(2q,k1)=1知d5=2,则由(29)式可知

又(pq-1)| a,故

又|A31|=p-1,故,此时

综上,由(28)和(30)式知:对于任意满足(p2-1)/│a且(pq-1)| a的a,均有

情形4 (p2-1)/│a且(pq-1)/│a时.
(A)gcd(2q,k)=1时,若(p-1)| a,则同余(1)式恰有p-1个解,且

故解集为

又满足gcd(2q,k)=1的k恰有φ(2q)=q-1个,故此时

若(p-1)/│a,则同余(1)式无解,此时

(B)gcd(2q,k)=2时,同余(1)式无解,此时

(C)gcd(2q,k)=q时,同余(1)式无解,此时

综上,由(33)~(36)式知:对于任意满足(p2-1)/│ a且的a,均有

故由(8)、(22)、(31)和(37)式知:对任意的a∈{1,2,…,p2q-2},均有

其中


近年来,零差分平衡函数被广泛应用于常组合码和差分系统中,同样,本文将零差分平衡函数做进一步研究之后,广义零差分平衡函数也可应用于常组合码和差分系统中,只是均很难达到最优.
[1]DING C S.Optimal constant composition codes from zero-differerce banlanced functions[J].IEEE Transactions on Information Theory,2008,54(12):5766-5770.
[2]DING C S.Optimal and perfecct difference systems of sets[J].J Combinatorial Theory,2009,116(1):109-119.
[3]POTT A,WANG Q.Difference balanced functions and their generalized difference sets[J].IEEE Transactions on Information Theory,2008,54(12):5766-5770.
[4]NYBEG K.Perfect Nonlinear S-boxes[M].Berlin:Springer-Verlag,1991.
[5]FENG T.A new construction of perfect nonlinear functions using Galois rings[J].J Combinatorial Designs,2009,17(17): 229-239.
[6]ZHA Z,KYUREGHYAN G M,WANG X.Perfect nonlinear binomials and their semifields[J].Finite Fields and Their Applications,2009,15(2):125-133.
[7]ZHOU Z,TANG X,WU D,et al.Some new classes of zero-difference balanced funtions[J].IEEE Transactions on Information Theory,2012,58(1):139-145.
[8]GE G,MIAO Y,YAO Z.Optimal frequency hopping sequences:auto-and cross-correlation properties[J].IEEE Transactions on Information Theory,2009,55(2):867-879.
[9]WANG Q,ZHOU Y.Sets of zero-difference balanced functionst and their applications[J].Adv Math Commun,2014,8(8):83-101.
[10]DING C S,TAN Y.Zero-difference balanced functions with applications[J].J Statistical Theory and Practice,2012,6(1): 3-19.
[11]DING C S,WANG Q,XIONG M S.Three new families of zero-difference balanced funtions with applications[J].IEEE Transactions on Information Theory,2013,60(4):2407-2413.
[12]YAN S Y.Elementary Number Theory[M].Berlin:Springer-Verlag,2002.
A Note on Generalized Zero-difference Balance Functions
JIANG Lin,LIAO Qunying
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
In this paper,by generalizing the definition of the zero-difference balanced functions to the generalized zero-difference balanced functions,a class of generalized zero-difference balance functions is constructed based on p-cyclotomic cosets,where p is a prime.
zero-difference balanced functions;generalized zero-difference balance functions;p-cyclotomic cosets
O156.1
A
1001-8395(2016)04-0484-07
10.3969/j.issn.1001-8395.2016.04.004
(编辑 郑月蓉)
2015-05-06
国家自然科学基金(11401408)、四川省应用基础研究计划项目(2016JY0134)和四川省教育厅自然科学重点项目(14ZA0034)
*通信作者简介:廖群英(1974—),女,教授,主要从事编码和密码学理论的研究,E-mail:qunyingliao@sicnu.edu.cn
2010 MSC:94A15;94A60;05B10
