万有引力莫非是几何效应？

赵峥，1967年毕业于中国科技大学物理系，1981年于北京师范大学天文系获硕士学位，1987年于布鲁塞尔自由大学获博士学位。曾任北京师范大学研究生院副院长、物理系主任、中国引力与相对论天体物理学会理事长、中国物理学会理事。现为北京师范大学物理系教授，理论物理博士生导师、教育学博士生导师。

等效原理揭示引力效应与惯性效应之间确实存在本质联系。

伽利略的自由落体定律告诉我们，在真空状态下，引力场中自由下落的各种小球，不管它们的物质组成（例如金球、石球还是木球），也不管它们的质量大小，下落规律都是相同的。推而广之，设想若干在真空引力场中做斜抛运动的小球，只要它们抛射的角度相同，离开弹射器时的初速也相同，那么不管它们的物质成分和质量大小如何，它们也将描出同样的轨迹。

我们知道，通常一个物体在外界环境中受到的外力大小，往往与物体的物质成分、物理状态有关。例如，一个物体在电磁场中受到电磁力的大小，与它是金属还是非金属，它是否带电，带电多少等有关。而且，不同物体在同一个电磁场中的运动轨迹，不仅和物体的物理成分及状态有关，也与它们的质量大小有关。但是引力场中的小球运动，居然与这些物理因素都无关，这是怎么回事呢？实在是太神奇了。

爱因斯坦意识到，万有引力不是一般的力，与我们通常熟悉的所有的力都不同。这是一种极为特殊的力。爱因斯坦反复思考这个问题，突然眼前一亮：万有引力莫非是一种“几何力”？莫非真如黎曼的推测，真实的空间可能是弯曲的？万有引力莫非是时空弯曲导致的几何效应？

爱因斯坦回忆起，在奥林匹亚科学院的活动中，他们几个年青人曾一起读过数学大师庞加莱的科普著作《科学与假设》。在那本书里，他们曾读到罗巴切夫斯坦和黎曼等发现的非欧几何，这一几何描述弯曲的空间。黎曼等数学家曾推测，真实的空间有可能不是平的，而是弯的，而且真实的空间有可能不是三维的，而是四维的，甚至更高维的。该书的内容曾使这几个年青人一连几个星期兴奋不已。

现在，爱因斯坦看到，黎曼等人的数学结果，竟然与自己当前研究的物理问题有关，这太让人兴奋了。

我们通常学习的几何，都是欧氏几何。欧氏几何产生于人类文明的发源地古埃及和两河流域，起源于河水泛滥后重新划分土地的需要，以及建筑等生产活动的需要。在公元前300年左右，在埃及亚历山大城工作的希腊数学家欧几里得把积累起来的几何知识集其大成，写成一部《几何原本》。我们中学学习的几何知识，都来源于此，都没有超出当年欧几里得的水平。

欧几里得几何以它概念的清楚、知识的丰富、逻辑的严密而著称。《几何原本》的全部知识建立在几条公设的基础上。全书从这几条公设出发，推出了全部几何知识。

在惊叹欧氏几何的完美的同时，有少数数学家觉得似乎它还有可以改进的地方。例如，一些人注意到它的“第五公设”，即我们通常所说的平行公设：

“过直线外一点，可以引，而且只可以引一条直线，与原直线平行（即不相交）。”

这些人觉得这条公设比其他公设都长，有点遗憾。于是有人试图从其他公设推导第五公设，如果能够推出，就可以取消这条公设，此公设的内容就可以当作定理了。这样，欧氏几何会显得更简洁，更完美。令人意外的是，这件工作十分困难。有关推导第五公设的尝试进行了1000多年，仍然没有进展。

到19世纪的时候，情况发生了变化，俄罗斯喀山大学教授罗巴切夫斯基做出了突破。他用反证法假设“过直线外的一点可以引两条以上的直线与原直线平行”，试图推出谬误。然而始终见不到谬误的影子。这时他的思想产生了一个飞跃：看来也可以用“过直线外的一点可以引两条以上的平行线”取代第五公设，从而建立起一套新几何，这套新几何应该是与欧氏几何并列的另一套几何体系。他非常兴奋，把有关的研究成果写成论文，寄给位于首都彼得堡的科学院。但是彼得堡科学院的数学家的思想都跳不出欧氏几何的束缚，都看不懂罗巴切夫斯基的论文。罗巴切夫斯基只好把自己的研究成果发表在喀山大学学报上。

由于喀山远离世界数学中心，没有人能看到罗巴切夫斯基的工作，于是他到欧洲内地宣传自己的学术观点。然而还是没有人肯定他的工作。他在德国作报告时，大数学家高斯参加了会议。年近9旬的高斯听完报告没有对他的新几何发表意见，只是建议德国科学院授予他通讯院士的称号。这是给予外国学者的最高荣誉，承认他是—位杰出的数学家，但没有具体对他的新几何发表看法。事后，高斯在自己的日记中，以及给朋友的信中都提到过罗巴切夫斯基的新几何。高斯说，他相信当时在会场上，只有他一个人听懂了罗巴切夫斯基的报告。实际上，高斯早就思考过类似的问题，得到过类似的成果。但是由于欧氏几何是教会推崇的，高斯胆小，他想到了哥白尼提出日心说的遭遇，于是决定对此保持沉默。

罗巴切夫斯基遗憾地回到家乡。后来他双目失明，在学生的帮助下完成了全部新几何的建立。他所创立的几何，被称为罗巴切夫斯基几何，简称罗氏几何。令他欣慰的是，他在逝世前，知道了自己的新几何已被数学界所承认。人们终于认识到存在一种不同于欧氏几何的新几何，称其为非欧几何。

不久之后，德国的黎曼采用另一条新公设取代第五公设，创建了另一种非欧几何。黎曼的新公设认为：“过直线外的一点，一条平行线也得不出来。”

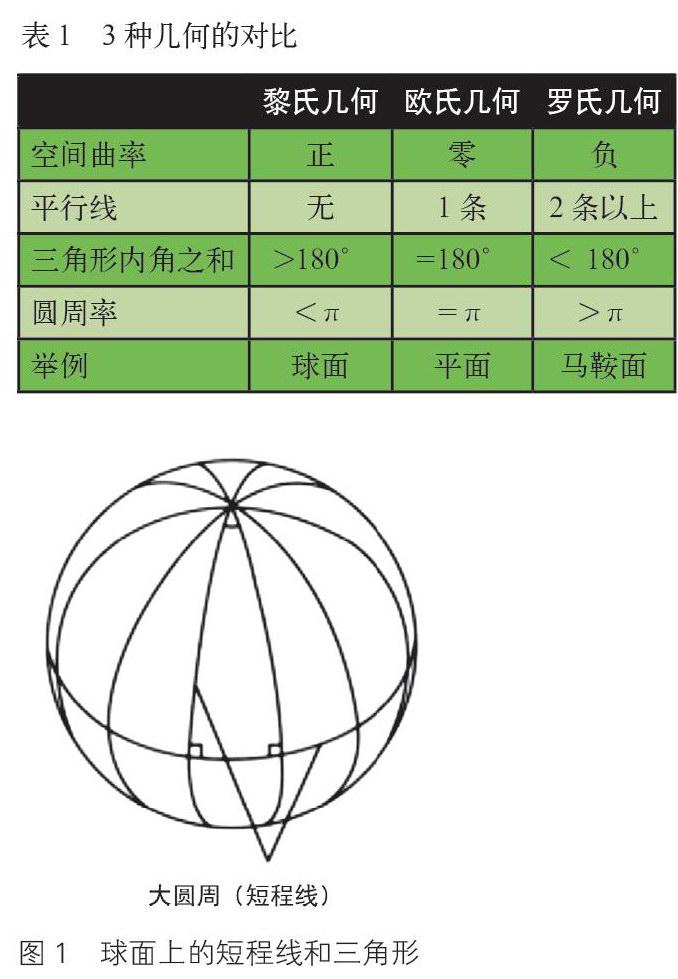
数学界很快认识到这3种几何都是正确的，它们反映不同曲率空间的性质。人们把罗巴切夫斯基创建的几何称为罗氏几何，把黎曼创建的几何称为黎氏几何。欧氏几何是平直空间中的几何，黎氏几何是正曲率空间中的几何，罗氏几何则是负曲率空间中的几何，这3种几何的特点列在表1中。

1845年，黎曼把这3种几何统一起来，统称为黎曼几何。他天才地预见到，真实的空间有可能不是平直的，物质的存在有可能造成空间的弯曲。由于当时的物理学还没发展到应用黎曼几何的水平，黎曼的预见还仅仅是一种猜测。

前面谈到的罗氏空间和黎氏空间都是弯曲空间，弯曲空间中怎么可能会有直线和平行线呢？实际上，弯曲空间中的直线并不是我们通常所说的直线，而是直线在弯曲空间中的推广。在欧氏几何中，直线定义为两点间的最短线。弯曲空间中的两点之间虽然不可能画出平常意义下的直线，但两点之间仍然存在最短线。在黎曼几何中，把两点之间的最短线称为短程线（又称测地线）。短程线，就是直线在弯曲空间中的推广。在空间平直的时候，短程线就恢复为我们通常看到的直线。

所谓平行线，就是两条不相交的直线。所以平行公设在罗氏几何中表述为：“在一条短程线之外，可以引两条以上的短程线与其不相交。”在黎氏几何中则表述为：“在一条短程线之外，不可能引出与其不相交的短程线。”

为了更好地理解黎曼几何，我们以球面为例加以解释。球面是正曲率的二维空间，在上面适用的是黎氏几何。研究表明，球面上的短程线为大圆周。在球面上任取两点A与B，再加上球心O，这三点可以决定一个平面，此平面与球面的交线就是大圆周。地球上的经线都是大圆周，赤道也是大圆周，但赤道之外的其他纬线都不是大圆周。

从北京飞往多伦多的飞机，从北京起飞后，不像一般人想象的那样直接向东越过太平洋，而是向东北方向飞，通过中国东北及俄罗斯远东地区，直奔白令海峡，然后沿阿拉斯加的北海岸飞行，再转向东南，通过加拿大东部，到达多伦多。有人可能会问，飞机为什么要绕圈子呢，直接往东飞不是近一点吗？干嘛要绕远呢？其实，飞机并没有绕远，飞机的航线恰好是北京、多伦多和地心这三点决定的大圆周，也就是说，恰好是北京和多伦多之间的短程线。

你可以想一想，能够过赤道外一点再作一个大圆周与赤道不相交吗？肯定不行。所以黎氏几何的平行公设在球面上完全正确。

再看一下球面上的三角形，它由三条短程线围成。如图1中，赤道和两条经线就围成了一个三角形。容易看出，所有的经线都与赤道垂直，三角形的两个底角之和已是180°了，再加上顶角，三内角之和肯定大于180°。