一种多芯片多输入PDN分布式建模及去耦方法

张　毅

(西安电子科技大学 CAD所，陕西 西安 710071)



一种多芯片多输入PDN分布式建模及去耦方法

张毅

(西安电子科技大学 CAD所，陕西 西安 710071)

摘要现阶段比较成熟的电源配送网络(PDN)分析方法多是针对单芯片单电源端口进行，无法满足高速系统多电源轨道的需求。文中通过对N端口网络的理论推导，分析了多电源端口PDN阻抗增加的原理，引入多输入阻抗的概念，用以精确捕捉PDN电流分布特性，进而提出了一种适用于多芯片多输入PDN的分布式建模方法，并给出复杂PDN整板去耦方案。实验例证表明，给出的去耦方案能有效地将所有芯片的多输入阻抗降低到目标阻抗之下，满足系统5%噪声容限范围要求。

关键词PDN；多芯片多输入；分布式建模；去耦

随着晶体管特征尺寸进入亚微米/纳米级别，高速系统芯片集成度不断提高，信号转换速率日益加快，导致电源噪声越发严重，这就对印制电路板上电源配送网络(PowerDeliveryNetwork，PDN)的去耦设计提出更严格的要求。现阶段比较成熟的PDN去耦分析多是针对单芯片单输入网络进行[1]，采用集总建模或近似分布式建模方法对互连网络的电气特性进行描述，无法准确捕捉高频范围内PDN电源端口间的相互影响和电流分布两种特性，也就无法对多芯片多输入PDN的去耦设计给出直观的指导意见。针对上述问题，本文基于高频范围内PDN的电流分布特性和阻抗增加原理，提出了一种新的多芯片多输入PDN分布式建模方法，并给出了复杂PDN去耦方法。

1建模分析

1.1PDN电流分布特性

复杂电路系统通常包含多个功能芯片，每个芯片又会封装多个电源地引脚。对于多电源端口的供电，系统会辟出专门的电源地平面以提供及时有效的功率传输。通常把电源地平面称为平面PDN。不同频率范围内，平面PDN的电流分布会表现出不同的特性。

在未添加去耦设计时，全部频率范围内，每个芯片端口的激励电流会平均分布在整个PDN平面上，此时PDN的电流分布表现为全局特性；对PDN添加去耦设计后，在低频范围内，平面PDN的电流分布仍表现出全局特性，随着频率升高，由于中高频去耦电容器可为其附近的电源端口提供及时有效的功率传输，使得高速电流回路在本地形成，芯片端口的激励电流不会扩散到整个平面，此时PDN的电流分布表现为本地特性。

工程师对复杂PDN的去耦设计应同时考虑平面PDN的这两种电流分布特性，因其直接关系着不同芯片电源端口的相互影响，否则就不能准确评估PDN由于电流叠加导致的回路阻抗增加及额外电源噪声，导致PDN去耦方案的欠设计。

1.2多输入阻抗提取

将多芯片多输入PDN看作一个N端口网络。图1(a)表示所有芯片同时分析时PDN的N端口等效网络，用以表征不同芯片电流叠加的影响，其中每个端口代表一个负载芯片。图1(b)表示只对其中的一个芯片分析时建立的N端口等效网络，用以捕捉同一芯片所有电源引脚电流叠加的影响，其中每个端口代表该芯片的一个电源地引脚。

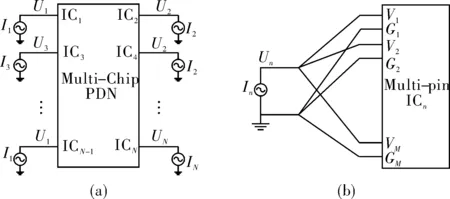
图1　多芯片多输入PDN的等效N端口网络

由欧姆定律，N端口网络输入输出矩阵方程为

(1)

其中，I1,…,IN为端口的激励电流；U1,…,UN为端口的外部压降；Zmn为端口间的互阻抗；Znn为端口n的自阻抗。端口自阻抗，即为单独使能芯片ICn时，芯片内部多对电源地引脚的电流相互叠加使得芯片端口感受到的阻抗。假设芯片ICn具有M对电源地引脚，激励电流为In，单独使能该芯片时外部压降为Un′，故端口n的自阻抗Znn为

(2)

由式(1)，对于具有N个负载芯片的PDN

Un=Zn1I1+Zn2I2+…+ZnNIN

(3)

可得芯片端口n感受到的PDN总阻抗为

(4)

上述芯片端口阻抗的提取过程中不仅通过自阻抗Znn包含了单个芯片内部所有电源地引脚之间的相互影响，且通过转移阻抗Zmn包含了不同芯片端口间的叠加影响，因此可同时捕捉平面PDN不同频率范围内所表现出的全局特性和本地特性。区别于传统PDN自阻抗的分析方法，这里引入多输入阻抗的概念，用以描述不同频率范围内平面PDN电流分布的全局特性和本地特性及对目标芯片回路阻抗的影响。

1.3分布式模型

多输入阻抗的提取过程中模型端口需要添加大小等于实际平均电流的激励源，这种激励方式在现有的FDM[2]、FEM[3]、FDTD[4]等分布式PDN建模方法中很难实现。由于HSPICE、ADS等电路仿真器中可方便完成激励源的添加[5]，因此应将PDN建模为其可识别的形式。二维分布式电路法可用于任何形状的PDN建模，也可方便添加任意数量的去耦电容器，便于瞬态分析和AC分析，具有较好的通用性。

以矩形平面对为例，该建模方法是把平面看作二维传输线，将其划分成很多单元栅格，每个单元格代表一个长度与宽度相等的平行板传输线[6]。其中，每个单元格中的每条传输线都可用集总元件建模为T模型或者π模型，如图2所示。

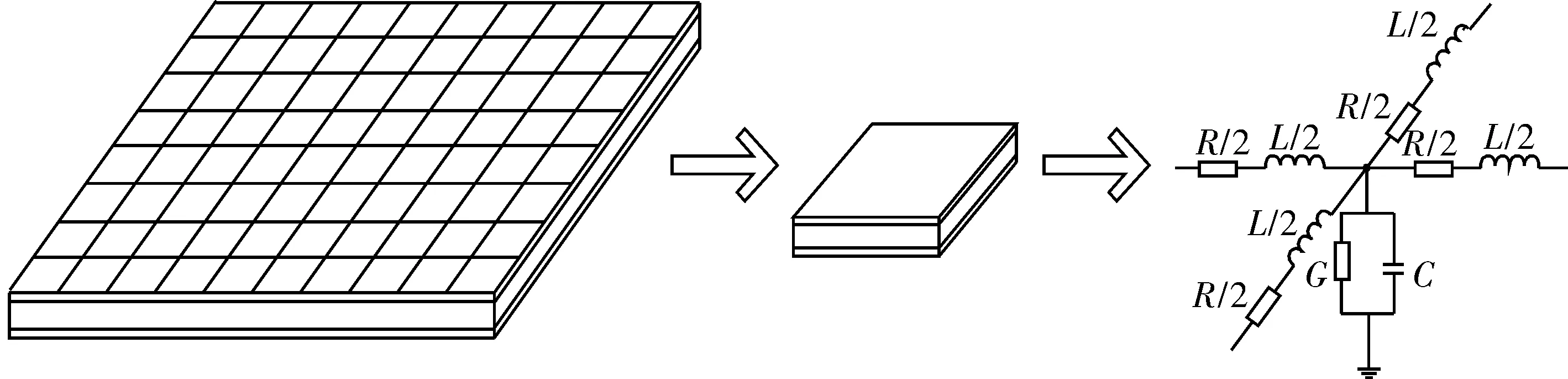
图2　PDN平面单元格划分及建模

首先将每个划分出来的单元栅格利用R、L、C和G建模为T型等效电路，然后再将建模后的所有单元栅格等效电路连接起来，构成一个二维分布式电路法SPICE等电路仿真器兼容的平面PDN等效模型，如图3所示。

由信号完整性相关知识[7]，单元格的参数计算如下

(5)

其中，ε0和μ0分别为自由空间中介电常数和磁导率；εr为相对介电常数；σc为电导率；w为单元格尺寸；d为两平面之间的间距；t为金属平面的厚度；f为频率；ω为角频率；tanδ为损耗角正切。

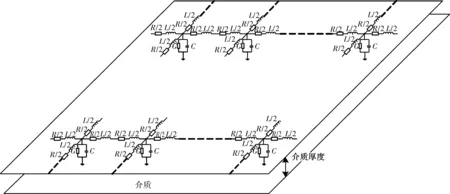
图3　复杂PDN二维分布式平面电路法模型

故有损介质非理想导体单元格的横向阻抗和纵向导纳可表示为

ZL=jωC+ωCtanδ

(6)

可以看出，该分布式模型的参数计算过程包含了PDN时延、损耗等高频分布效应，并方便添加多端口激励模式，因此可全面表征不同频带范围内PDN的电流分布特性，用于多输入阻抗的准确提取。

2去耦方法及验证

基于前面复杂PDN多输入阻抗分析和分布式建模方法，给出以下适用于多芯片多电源端口PCB板的去耦方法：(1)查阅相关资料，获取待去耦PCB的系统工作信息，包括不同芯片的输入电压、平均电流、噪声容限。确定去耦截止频率；(2)对于同一电源地平面上的所有负载芯片，将其看作一个N端口PDN，其中每个芯片的位于该电源地平面上的所有电源地引脚看作一个总端口；(3)选择具有最大工作电流、最多电源地引脚数目的芯片作为去耦目标芯片。对于两者条件不能同时满足的情况，可折衷选择；(4)利用二维分布式电路法建立选取的N端口PDN的分布式模型。建模时每个芯片端口要加上大小等于实际平均电流的激励源；(5)HSPICE或SIWAVE、ADS联合仿真，提取目标芯片的多输入阻抗曲线，包括幅度和相位信息；(6)有理函数矢量拟合，拟合仿真得到的目标芯片多输入阻抗曲线的有理函数[8]，用于去耦设计的数值评判标准；(7)基于目标芯片多输入阻抗函数，利用最大违背点去耦选电容算法[9]，给出电容器选择方案；(8)将(7)中得出的电容器选择方案加载到(4)中建立的N端口PDN分布式模型中，仿真验证此时的目标芯片多输入阻抗是否低于目标阻抗。同时验证SSN噪声是否在芯片噪声容限范围之内；(9)逐一验证该电容器选择方案对其余芯片去耦效果。如果针对某一距离较远芯片去耦设计不足，在该选择方案基础上，重新计算此时PDN芯片端口回路阻抗，重复步骤(4)～(9)后续添加。

实验板仿真验证该去耦方法的有效性。简便起见，设计一具有两个芯片的PCB板，同一电源地平面上芯片IC1具有8个电源引脚，额定输入电压3.3V，平均电流4A；芯片IC2具有4个电源引脚，平均电流2A。实验板大小60mm×80mm，介质材料FR4，损耗常数 为0.02，板层厚度0.2mm。实验板如图4所示。

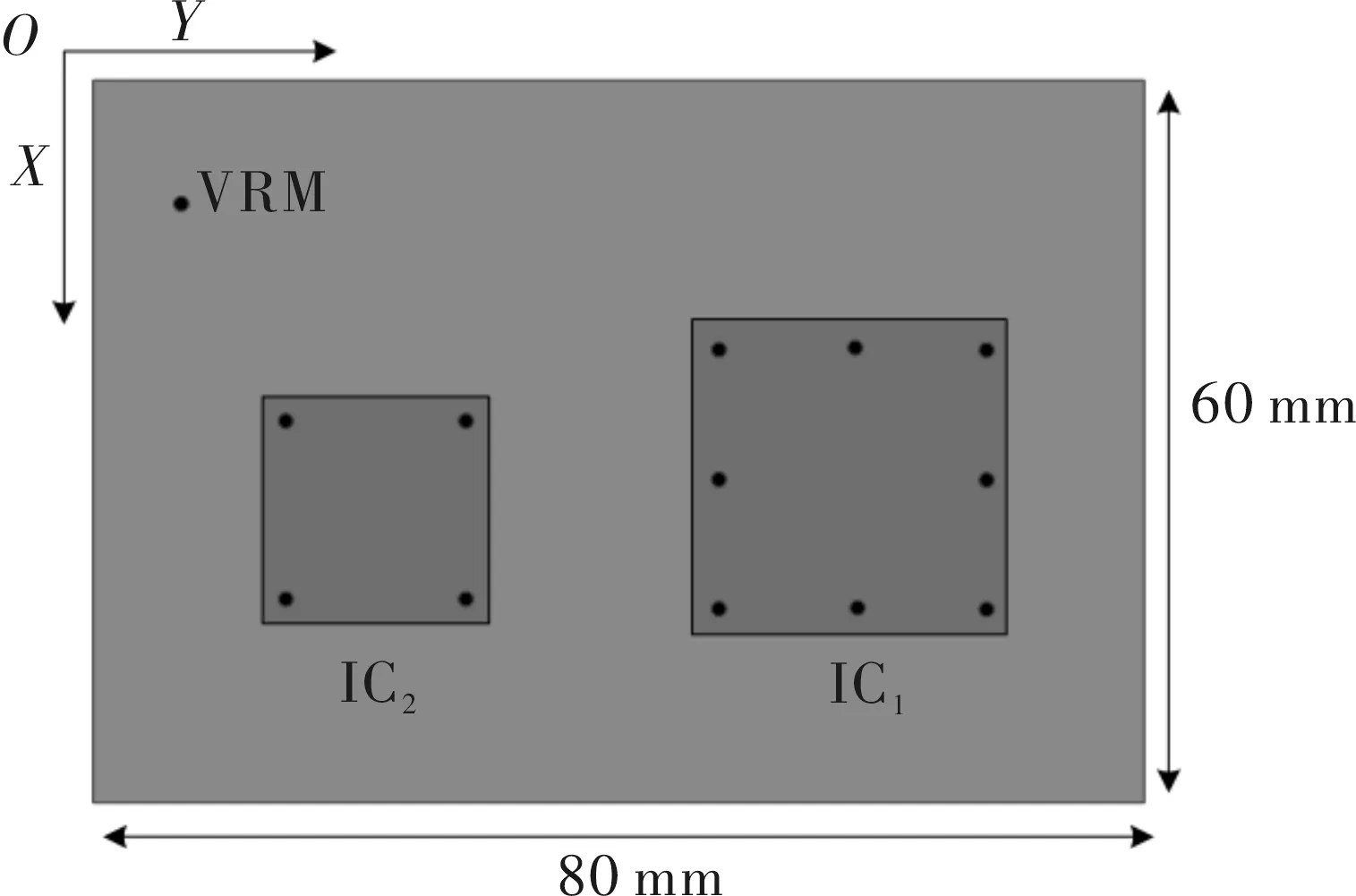
图4　复杂PDN去耦实验板

利用论文介绍的二维分布式电路法对该PDN进行建模，并仿真提取未去耦时两芯片的多输入阻抗。仿真结果如图5所示，其中，实线代表多输入阻抗曲线，点划线代表传统单端口PDN分析的自阻抗曲线。

可见，PDN基于多输入阻抗概念和分布式模型得到的芯片端口阻抗远大于传统单端口分析的自阻抗，说明了该阻抗提取方法的精确性。将芯片IC1选作去耦目标芯片，对仿真得出的多输入阻抗曲线进行矢量拟合，得到IC1端口阻抗函数为

(7)

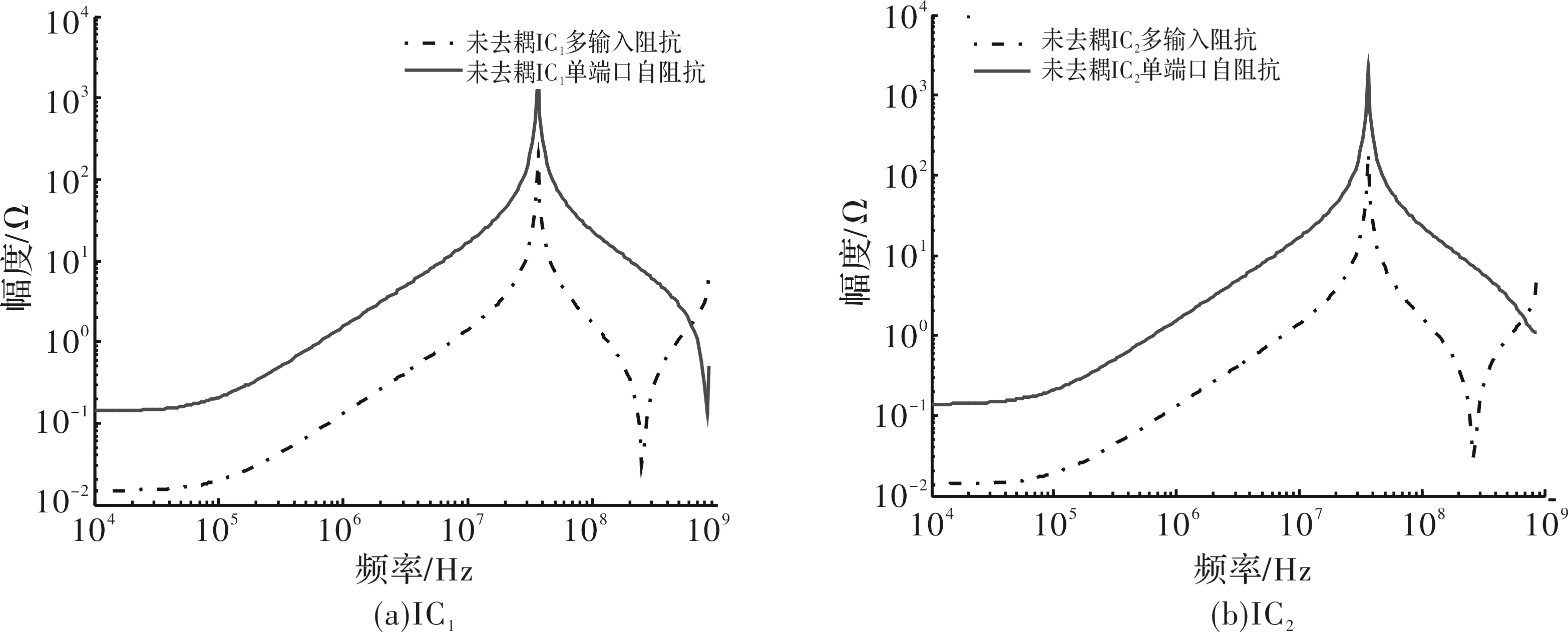
图5　未添加去耦电容器时的多输入阻抗和单端口自阻抗

利用本文提出的去耦方法，选择出的电容器组合如表1所示。

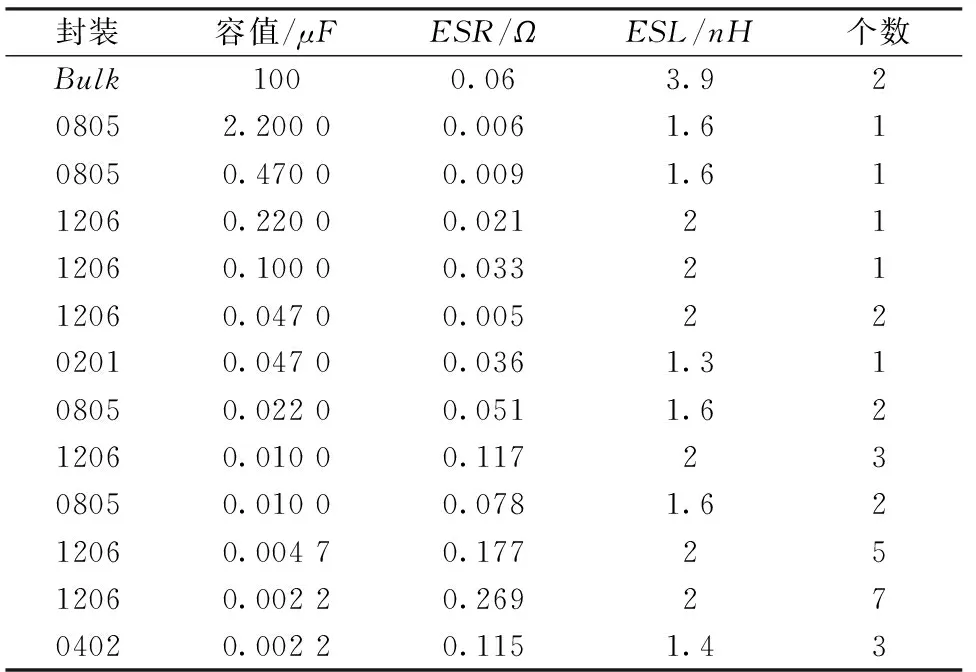
表1　基于整板去耦方案的电容器选择

将实验板添加上表选择出的去耦电容器组合方案，ADS中仿真得到此时芯片IC1、IC2阻抗及电源噪声如图6所示。其中，图6(a)实线代表未去耦时芯片IC1多输入阻抗，虚线代表添加去耦设计后芯片IC1多输入阻抗，点划线代表去耦后IC2多输入阻抗；图6(b)点划线代表去耦后芯片IC1电源噪声，实线代表去耦后芯片IC2电源噪声。

由此可见，论文提出的基于分布式建模的多芯片多输入PDN去耦方案在去耦截止频率范围内可有效地将芯片IC1和IC2的多输入阻抗均降低到目标阻抗以下，并将芯片电源噪声控制在5%噪声容限范围之内。

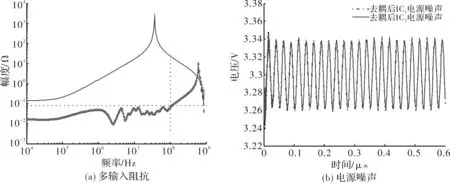
图6　添加去耦设计后芯片IC1、IC2的测量曲线

3结束语

当今业界对复杂PDN的去耦设计还没有形成一套系统的解决方法。本文基于PDN分布式建模给出了一种适用于多芯片多电源端口的PDN去耦方法，选择出的电容器组合可有效控制PCB板上电源噪声，对实际工程去耦具有较高的实用价值。该方法将复杂PDN的去耦设计流程化，提高了PDN设计效率，降低了成本。

参考文献

[1]斯瓦米纳坦·恩金.芯片及系统的电源完整性建模与设计[M].李玉山,张木水,译.北京:电子工业出版社,2009.

[2]MondalM,ArchambeaultB,JandhyalaV.Enablingearlydesignofcomplexpowerdeliverynetworksusingspatially-nonuniformfinite-differencemethod[C].SantaClara:DesignConference, 2010.

[3]EnginAE,BharathK,SwaminathanM.Multilayeredfinitedifferencemethodformodelingofpackageandprintedcircuitboardplanes[J].IEEETransactionsonElectromagneticCompatibility,2007,49(2): 441-447.

[4]FangJ,RenJ.Locallyconformedfinite-differencetime-domainalgorithmofmodelingarbitraryshapeplanarmetalstrips[J].IEEETransactionsonMicrowaveTheoryandTechniques,1993, 41(5):830-838.

[5]阎照文.信号完整性仿真分析方法[M].北京:中国水利水电出版社,2011.

[6]张木水,李玉山.信号完整性分析与设计[M].北京:电子工业出版社,2010.

[7]EricBogatin.信号完整性分析[M].李玉山,李丽平,译.北京:电子工业出版社,2005.

[8]BjemGustavsen,AdamSemlyen.Simulationoftransmissionlinetransientsusingvectorfittingandmodaldecomposition[J].IEEETransactionsonPowerDelivery,1998,13(2):605-614.

[9]刘婷婷.电源分配网络分析及电容器精确建模[D].西安:西安电子科技大学,2011.

A New Distributed Modeling and Decoupling Method for Multi-chip Power Delivery Network

ZHANGYi

(InstituteofElectronicCAD,XidianUniversity,Xi’an710071,China)

AbstractAt the present stage more mature decoupling analyses of PDN aim mostly at the single chip and single input network, failing to meet the analysis requirements of the increasingly high-speed and highly integrated system. Based on the N-port network theory, this paper analyzes the principle of resistance increases for multi-power port PDN, introduces the new concept of multi-input impedance in order to catch the distributed characteristics of PDN current, and gives the decoupling method for complex PDN finally. The experimental results prove that the proposed decoupling scheme can reduce multi-input impedance of all the chips to below target impedance effectively to meet the requirements of the system 5% noise margin.

KeywordsPDN; multi-chip and multi-input; distributed modeling; decoupling method

收稿日期:2015- 11- 10

作者简介:张毅(1988-)，男，硕士研究生。研究方向：电源完整性。

doi:10.16180/j.cnki.issn1007-7820.2016.07.038

中图分类号TN919.2

文献标识码A

文章编号1007-7820(2016)07-132-05