智能PID控制算法研究及Matlab实现
2016-07-23蔡淑敏王亚刚
蔡淑敏,王亚刚,田 涛
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海华虹集成电路有限责任公司,上海 201203)
智能PID控制算法研究及Matlab实现
蔡淑敏1,王亚刚1,田涛2
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海华虹集成电路有限责任公司,上海 201203)
摘要针对滞后大、非线性等复杂的系统,常规PID控制算法已无法满足控制任务要求。为解决此类问题,文中提出从智能PID控制中的模糊PID控制、BP神经网络PID控制着手,仿真比较智能PID控制与常规PID控制的控制结果。实验表明,智能PID控制的超调量可达到0,稳定时间也大幅缩短,使系统整体的动静态特性得到了有效地改善。
关键词PID控制;智能控制;模糊控制;神经网络;Matlab仿真
现代工业生产复杂,被控对象多具有时变性和复杂的非线性,常规PID控制的数学模型不能精准建立,也不能在线自整定,因此难以满足闭环优化控制[1]的要求。
在现实操作过程中,熟练的操作人员可根据控制理论以及自身的操作经验解决复杂的控制系统,智能控制也由此产生。本文重点从智能PID控制[2]中的模糊PID控制[3]以及神经网络PID控制[4]出发解决实际问题。
智能控制是较高级的控制,对于复杂的系统控制问题,能自动调整参数,优化参数,有效达到控制效果[5]。适合于不确定性对象的控制,其不确定性是不了解模型、模型的参数和结构变化范围大;对于非线性系统的控制问题,智能控制方法能较好的解决;同时适合于复杂的任务要求,比如在复杂的控制过程中,既要实现对各被控物理量定值调节外,还要求能自动处理各种故障[6],如系统的启、停等功能。
1常规PID控制
PID控制是指比例、积分和微分控制的结合[7]。其原理如图1所示,控制信号是3个作用分量之和,并输出给被控对象,根据PID调节的作用,进行微分和比例以及积分的3个运算作用于误差信号 。

图1 PID控制器的结构原理图
PID控制器的数学模型是
(1)
式中,控制器的输出信号是u(t),是为被控对象所用的;r(t)是给定的输入信号;系统的被控量是c(t),误差e定义为:e(t)=r(t)-c(t)。
传递函数的模型是
(2)
式中,ki是积分时间常数;kp是比例系数;kd是微分时间常数。
根据式(2)可得,3个参量kp、ki和kd是PID控制作用的中心点。设一被控对象为二阶系统,其传递函数模型是
(3)
利用Matlab仿真分析得到常规PID控制器的控制效果,仿真结果如图2所示。从图可看出在比例、积分、微分共同作用下,经过最终的参数调整,在kd为0.5时,上升时间是0.24s,稳定时间是3.02s。
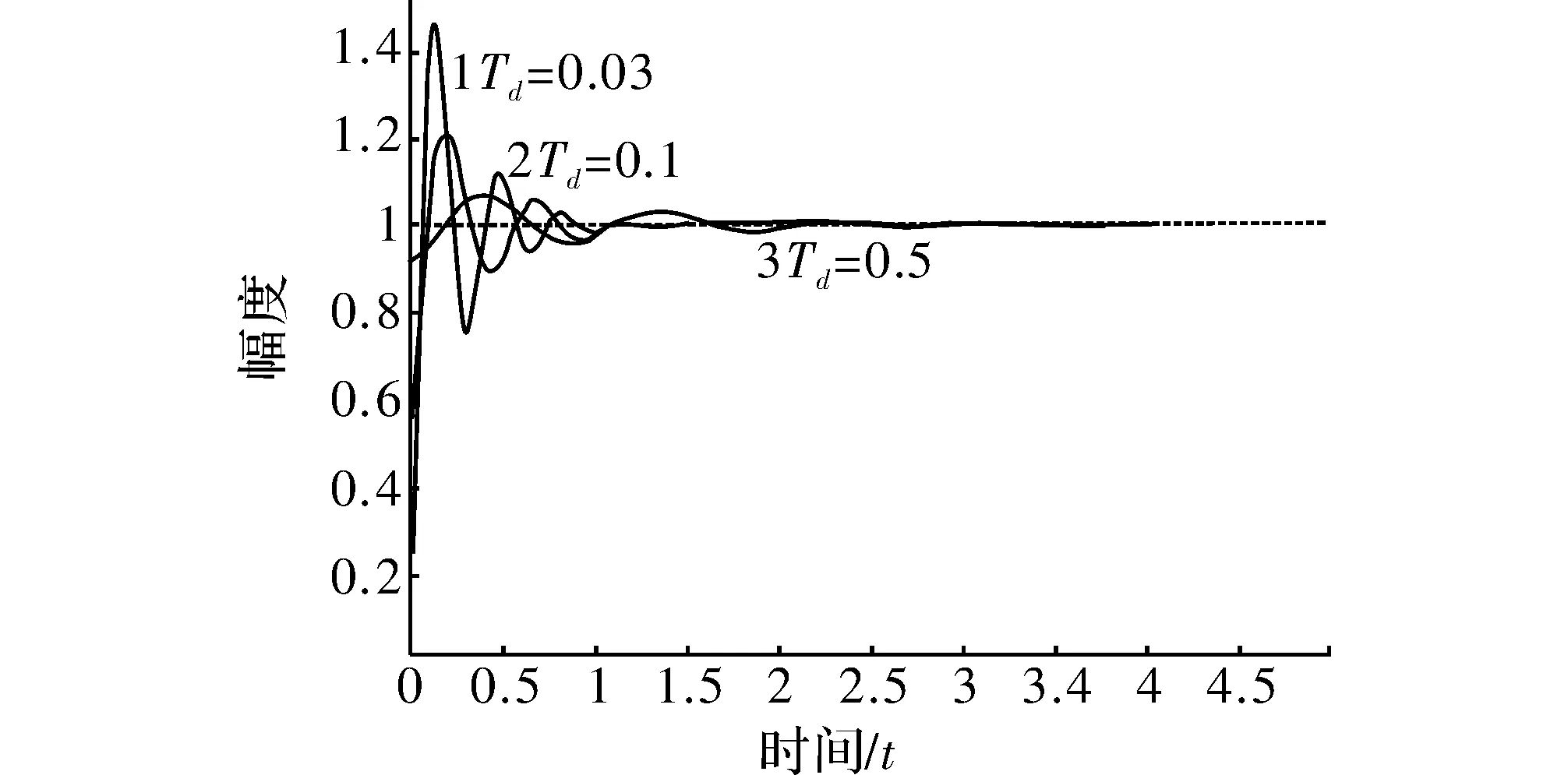
图2 系统PID控制阶跃响应曲线
2智能PID控制
2.1模糊PID控制器的设计与仿真
模糊控制的基本原理框图[8]如图3所示。其控制方法的基础是建立在模糊语言变量、模糊集理论以及模糊逻辑推理上的,模仿人的推理决策。根据专家的经验编写成模糊规则,模糊规则的输入即为在模糊化传感器上实时信号得来的信号,进而完成模糊推理,并把模糊推理以后而得到的输出量,加在执行器上。如图3中虚线框内所示,其中模糊控制器是核心部件。
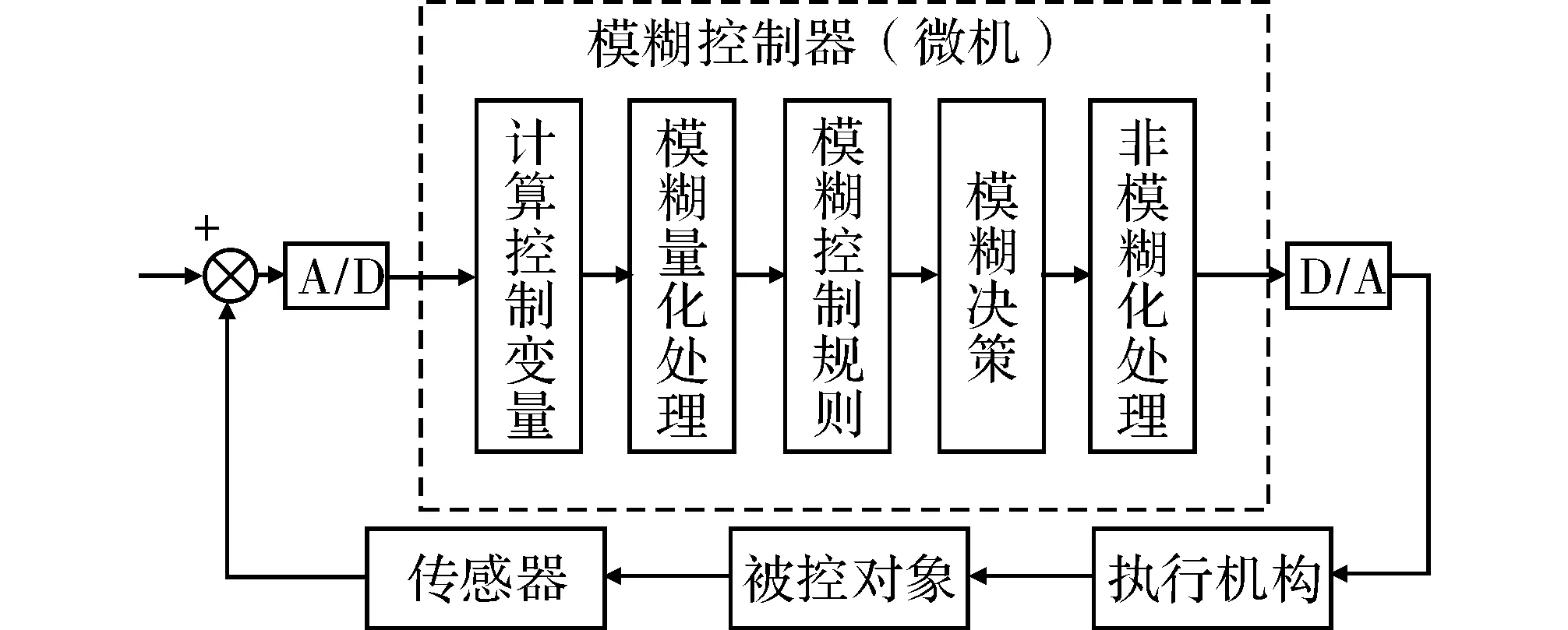
图3 模糊控制的基本原理框图
误差e和误差变化ec作为自适应模糊PID控制器的输入,在模糊控制规则在线的情况下以及适当范围内,根据模糊控制原理,不断的检测误差e和误差变化ec,修改3个参数,以此来满足控制参数在不同的误差e和误差变化ec下的不同要求,使得系统性能达到良好的状态。
在本实验中将系统误差e的模糊范围定义为(-3,+3),即当误差在这个范围内时,模糊控制器开始作用。将系统e和误差变化率ec的变化范围定义为模糊集上的论域
e,ec={-5,-4,-3,-2,-1,0,1,2,3,4,5}
其模糊子集为
e,ec={NB,NM,NS,O,PS,PM,PB}
子集里的元素分别表示的是负大、负中、负小、零、正小、正中、正大。假设kp、ki、kd和e、均服从正态分布。将PID的3个参数kp、ki、kd的范围分别定义为
(4)
由以上可得出各个模糊子集的隶属表[9],并建立合适的模糊规则表,得到针对kp、ki、kd3个参数分别整定的模糊规则表。
根据各个参数的模糊控制模型和各个模糊子集的隶属度赋值表,应用模糊合成推理的设计PID修正参数的模糊矩阵表,查修正参数带入下式计算
(5)
采用同一被控对象,采样的时间是1ms,在第300个采样时间控制器输出加1.0的干扰,根据模糊原理,利用Matlab进行仿真的结果如下:图4是模糊PID控制的阶跃响应曲线,最终的上升时间是0.12s,稳定时间是0.34s。图5是模糊PID控制通过自适应调整使误差趋于零的变化过程。
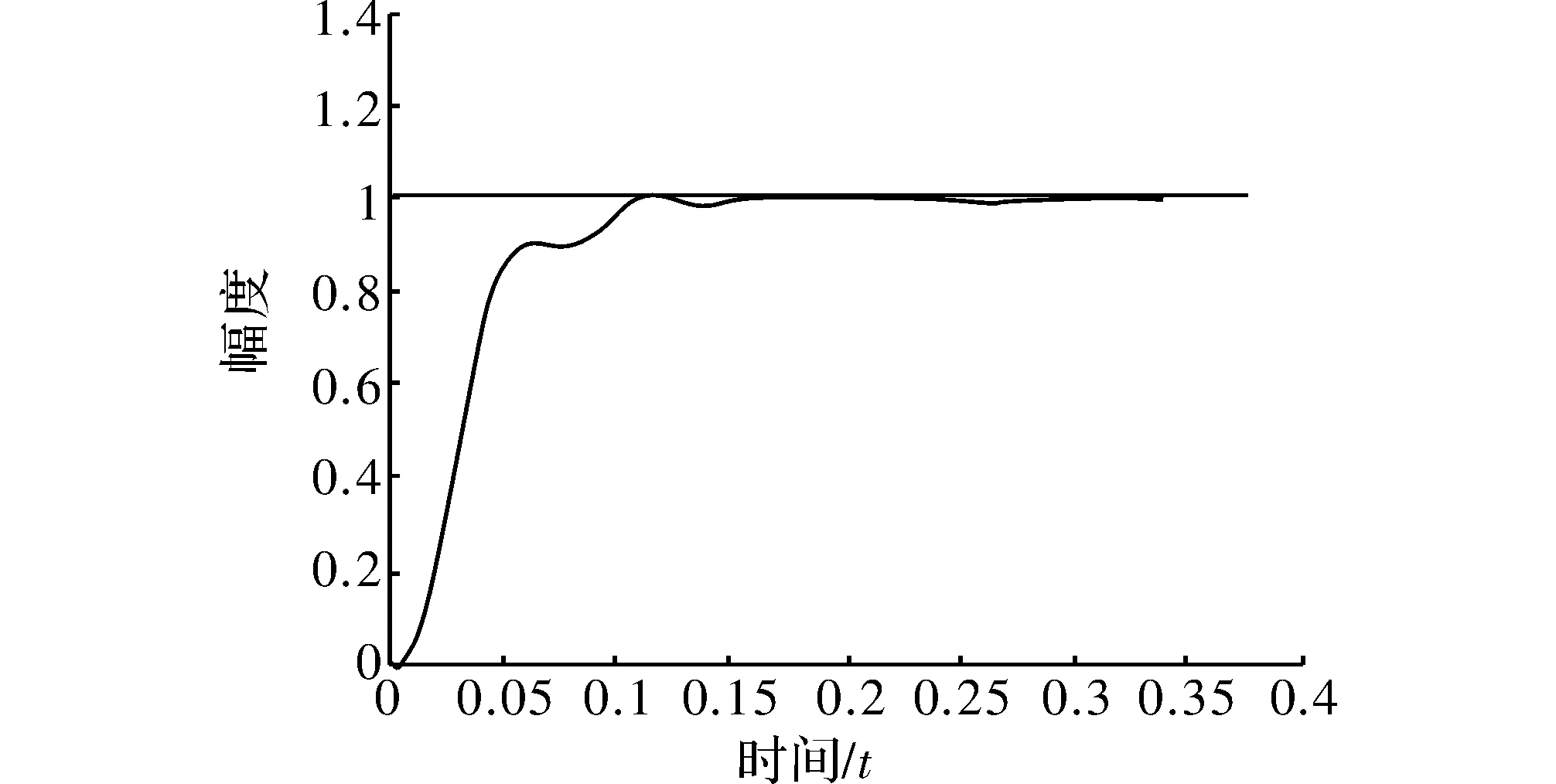
图4 模糊PID控制阶跃响应
2.2神经网络PID控制
神经网络是作为现代的信息处理技术的一种,其对时变、复杂的非线性系统建立精准的数学模型,在线自整定,满足闭环优化控制的要求,从而达到较好的控制效果。神经网络PID控制下有诸多分类,本实验采用BP神经网络的PID控制。
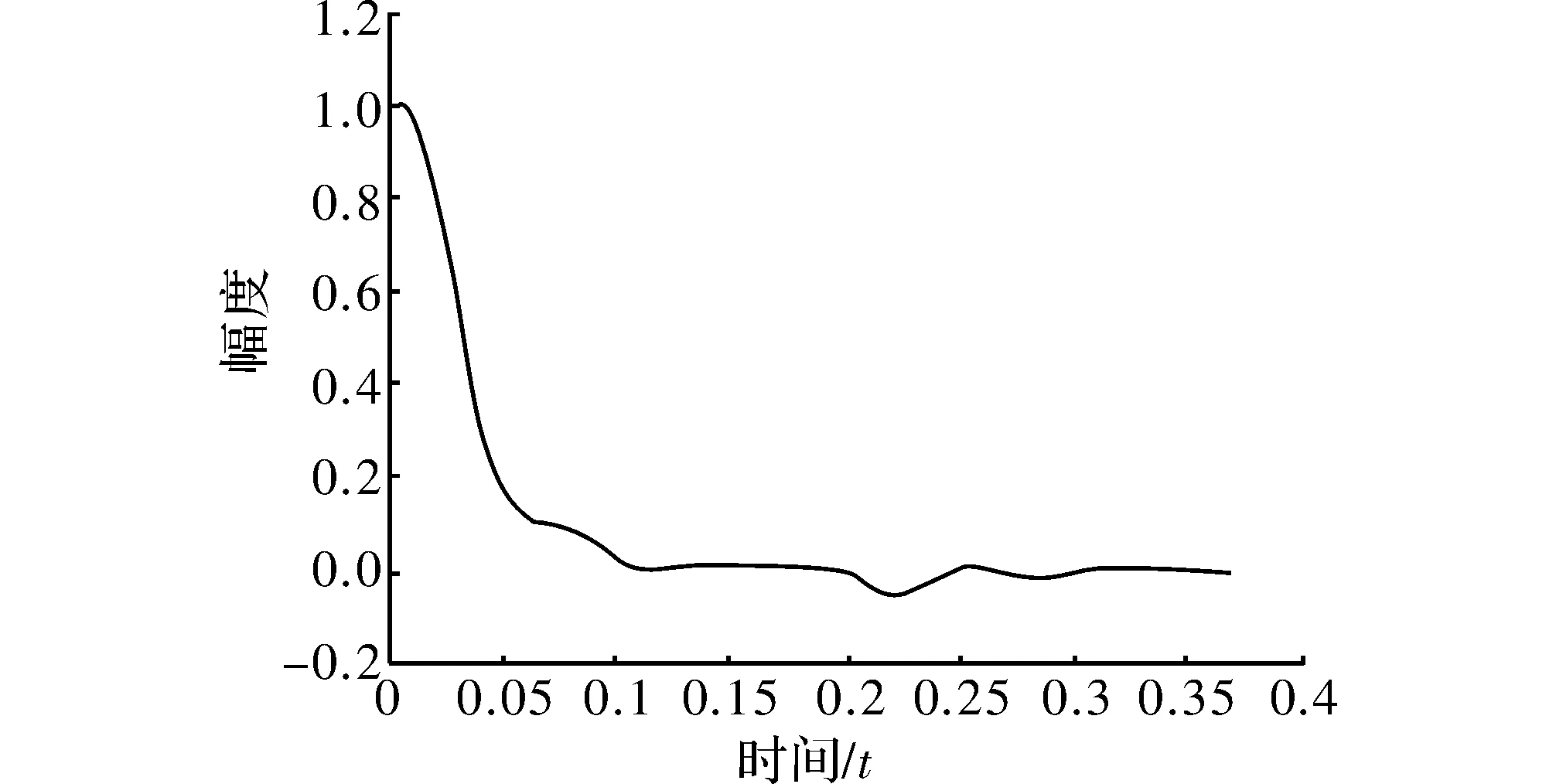
图5 模糊PID控制误差响应
BP神经网络具有任意非线性表达能力,不仅结构简单,学习算法也简洁明确,其结构如图6所示。控制器的输出部分主要由两部分构成[10],一是常规PID控制器,二是神经网络NN,其作用是根据系统运行状态,使3个参数可自行调整,输出最优控制下的PID控制器参数[11]。

图6 基于BP神经网络的PID控制系统结构
增量式数字PID控制算法如下
(6)
如图7所示,是3层BP网络。网络输入层节点对应所选系统运行状态量,若系统在不同时刻的输入输出量,比要时应进行归一化处理,各节点状态如图7所示。
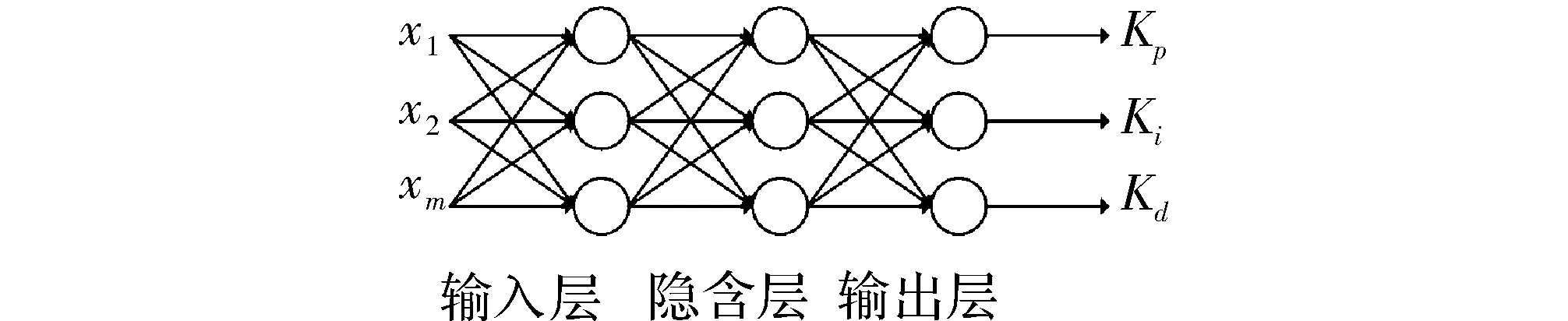
图7 3层BP网络结构
(7)
式中,输入变量个数M取决于被控系统的复杂程度。
网络隐含层的输入输出关系为
(8)
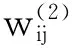
(9)
则隐含层加权系数的学习算法
(10)
(11)
网络输出层各节点输入输出关系为
(12)
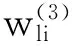
则网络输出层权系数的学习算法是
(13)
(14)
综上所述,基于BP网络PID控制器控制算法的步骤为:

(2)通过采样得到y(k)和yr(k),计算该时刻的误差e(k)=yr(k)-y(k);
(3)归一化处理系统不同时刻的输入输出。误差和控制量,作为网络的输入;
(4)由式(3)和式(6)计算网络NN各个层神经元输入、输出,NN输出层的输出便是PID控制器3个可调整参数kp、ki、kd;
(5)由式(2)计算控制器输出u(k);
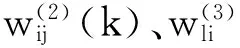
(7)令k=k+1,返回步骤(2)。
被控对象的数学模型为
(15)
进行Matlab仿真,学习速率η=0.06,平滑因子α=0.05,开始时,kp=11、ki=0.02、kd=9,仿真结果如图8所示,其中线条1即是经过BP网络整定PID的3个参数后,系统的单位阶跃响应曲线;线条2是未整定参数系统的单位阶跃响应曲线。
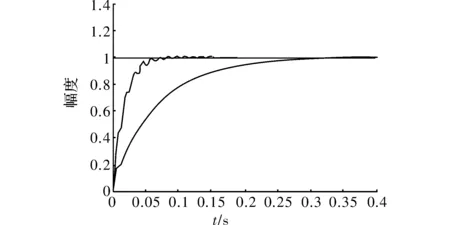
图8 阶跃响应曲线
3结束语
针对以上仿真结果整理成表格,如表4所示。从表格的数据可看出,常规PID控制难以达到最优的控制效果,对同一个模型而言,其上升时间、稳定时间均比智能PID控制要长,常规PID控制对参数的优化,是需要人工动手选择操作的,这对复杂的控制系统来说,任务繁重,几乎不可能实现。而模糊PID控制可自适应调整优化参数,且使误差趋于0;BP神经网络PID控制可在线对自行参数进行调整,最后使得系统性能达到良好的控制效果。
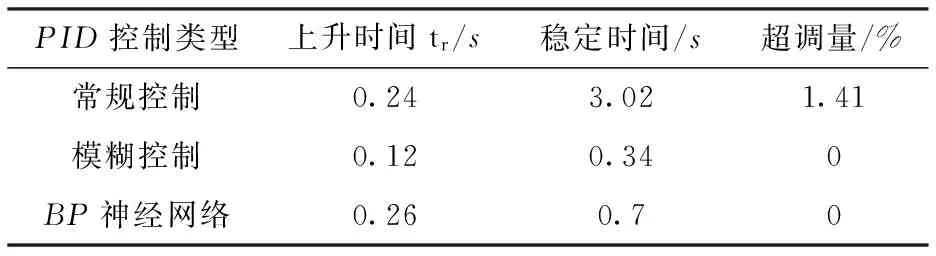
表4 常规PID控制与各智能PID控制的比较
参考文献
[1]刘金琨.先进PID控制Matlab仿真[M]. 3版.北京:电子工业出版社,2011.
[2]腾飞.智能PID控制器的设计和仿真[D]. 哈尔滨:哈尔滨工业大学,2011.
[3]李茜,李彬,朱雪丹.模糊自整定PID控制器的设计与仿真[J].化工自动化及仪表,2010,37(3):25-28.
[4]师黎,陈铁军,李晓媛,等.智能控制理论及应用[M].北京:清华大学出版社,2009.
[5]韦巍.智能控制技术[M].北京:机械工业出版社,1999.
[6]李士勇.模糊控制·神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.
[7]诸静.模糊控制原理与应用[M].北京:机械工业出版社,1995.
[8]高德欣,魏蕊,唐功友.非线性系统近似最优PD动态补偿控制[J].控制理论与应用,2011,28(12):1837-1842.
[9]王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社,2003.
[10]刘强,扈宏杰,刘金琨,等.基于遗传算法的伺服系统摩擦参数辨识研究[J].系统工程与电子技术,2003,25(1):77-80.
[11]窦艳艳,钱蕾,冯金龙. 基于Matlab的模糊PID控制系统设计及仿真[J].电子科技,2015,28(2):119-122.
[12]李娟.一种基于前馈补偿的PID轨压控制设计方法[J].电子科技,2014,27(6):146-149.
Research on Intelligent PID Control Algorithm and Matlab Simulation
CAIShumin1,WANGYagang1,TIANTao2
(1.Schoolofoptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,
Shanghai200093,China; 2.ShanghaiHuahongIntegratedCircuitCo.Ltd.,Shanghai201203,China)
AbstractWith the rapid development of modern industry, the conventional PID control algorithm can not meet the requirements of the control task. In order to solve these problems, the fuzzy PID control and BP neural network PID control are included in intelligent PID control for simulation and comparison of the control results of the intelligent PID control and conventional PID control. The experiments show that the overshoot of the intelligent PID control can reach 0 with the stability time greatly shortened and the dynamic and static characteristics of the system improved.
KeywordsPID control; intelligence control; fuzzy control; neural network; Matlab simulation
收稿日期:2015- 11- 07
作者简介:蔡淑敏(1993-),女,硕士研究生。研究方向:嵌入式芯片等。王亚刚(1967-),男,博士,硕士生导师。研究方向:工业过程控制等。田涛(1979-),男,教授级高工。研究方向:嵌入式。
doi:10.16180/j.cnki.issn1007-7820.2016.07.013
中图分类号TP273+.5
文献标识码A
文章编号1007-7820(2016)07-043-04
