基于BP神经网络的霍普菲尔德模型改进研究

朱明晨,赵　平,陈伟荣

(1.铜陵学院 建筑工程学院，安徽 铜陵 244061；2.东南大学 交通学院，江苏 南京 210096)



基于BP神经网络的霍普菲尔德模型改进研究

朱明晨1,赵平1,陈伟荣2

(1.铜陵学院 建筑工程学院，安徽 铜陵 244061；2.东南大学 交通学院，江苏 南京 210096)

摘要：为了分析对流层延迟的时空变化规律、提高对流层延迟的改正精度,利用BP神经网络处理非线性问题的优势，改进传统的霍普菲尔德模型得到一种新的融合模型(Hop+BP模型)。分别对比Hop+BP模型与传统的霍普菲尔德模型、多元线性回归模型、BP神经网络等模型的计算结果，得到如下结论：霍普菲尔德模型存在一个明显的系统误差，精度较低；多元线性回归的预测精度有所提高，但是其本质是将数据强制拟合，缺少物理解释，难以推广使用；传统的BP神经网络的计算精度较之霍普菲尔德模型有80%的提高，但存在明显的不稳定性；Hop+BP模型具有预测精度高、稳定性好等优点，预测中误差为1.1 cm，明显优于传统方法。

关键词：霍普菲尔德模型；BP神经网络；多元线性回归；精度分析

随着各国卫星大地测量技术的快速发展，GNSS导航定位系统应用的广度和深度都在不断扩展和加深，与此同时对该系统的精度要求也在不断提高，精确计算对流层延迟不仅可以大幅度提高GNSS导航和定位的精度，还可以转换求得大气中的水汽含量进而反演大气可降水量，同时还可以校正InSAR图像以提高遥感图像的质量。目前计算对流层延迟的经验模型主要有：霍普菲尔德模型、萨斯塔莫宁模型、勃兰克模型以及基于数值天气预报模型的EGNOS、UNB3模型等[1]。由于对流层所处的海拔较低，且变化复杂，属于非弥散性介质，导致对流层延迟是一个非线性的物理量，难以用一个固定的函数模型描述特定时间、特定地点、特定环境下对流层大气误差的真实情况。BP神经网络属于自适应非线性动力学系统，具有学习、记忆、计算和各种智能处理的功能，已经成为解决许多非线性问题的一种必要的技术手段[2]。本文尝试将BP神经网络与传统的经验模型融合，利用我国部分城市的气象数据，对比分析霍普菲尔德模型、多元线性回归模型、BP神经网络以及Hop+BP模型这4个模型的计算精度，得出有益的结论。

1霍普菲尔德模型的基本原理

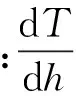
(1)

式(1)前半部分为干延迟，后半部分为湿延迟。式中:Ps与es分别为测站的气压与水汽压，单位为mbar；Ts为测站的绝对温度；hs为测站的海拔高度；hw取11 000 m；有文献将hd称作是对流层顶，可以用式(2)来计算。

hd=40 136+148.72(T-273.16).

(2)

霍普菲尔德模型形式简单，仅需要测站的地面气温、气压、水汽压及海拔高度就能很好地估计测站的对流层天顶干延迟，但由于水汽分压变化复杂，其湿延迟的估计精度并不理想。

2BP神经网络的基本原理

神经网络是由简单处理单元构成的大规模并行分布式的处理器，通过模仿人脑处理信息的物理过程，具有储存经验知识进而分析计算的特性，并因此具有很强的泛化能力。所以在处理非线性复杂问题时，神经网络有其独特的优势。

BP神经网络是众多神经网络模型中最为常见的一个，常用的单隐含层BP神经网络模型结构如图1所示。

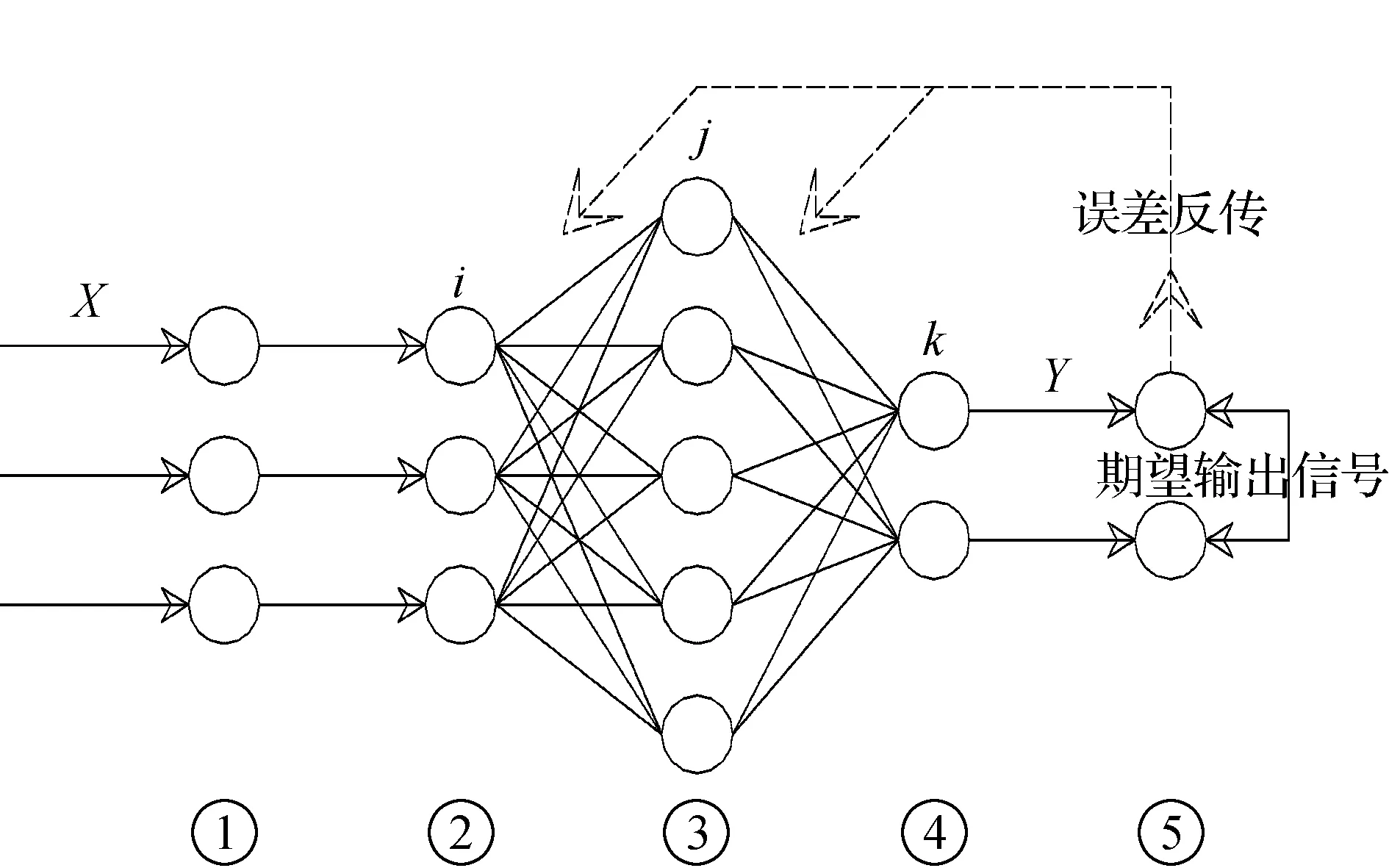
图1　BP神经网络模型结构图

图1中，第①层为输入层转换层，第②层为输入层，第③层为隐含层，第④层为输出层，第⑤层为输出层转换层。BP神经网络模型分为学习和预测两个过程。学习过程(监督学习)即是利用学习样本对神经网络的突触权值进行修改的训练过程。每个学习样本由唯一的输入信号和相应的期望响应

组成。从样本集中选取一个样例提供给网络，网络就相应地调整它的突触权值，使期望响应和由输入信号以适当的统计准则产生的网络实际响应之间的差别最小化[2]。当所有学习样本的期望响应及其网络实际响应之间的差别都在允许误差之内，且网络对突触权值没有明显的修正达到稳定状态时，学习过程结束。此时保存网络的突触权值，即可进行计算。

3BP神经网络模型的建立

3.1网型结构的确定

除第①和第⑤层外，确定神经网络的网型结构主要是确定输入层节点的个数、隐含层节点的个数以及输出层节点的个数。输出层节点数的确定比较简单，一般工程应用中都取1，若有多个输出，可以通过构造多个单输出网络分别研究。本文构造用于计算对流层延迟的神经网络，输出层为对流层延迟δ。

输入层一般取决于影响样本值的参数，可以通过主成分分析确定。考虑到数据源的形式以及霍普菲尔德模型的推导过程，本文选取的输入层为：测站的海拔高度hs,气压Ps,绝对温度Ts以及露点温度td。

隐含层节点数的确定比较复杂，没有现成的公式可以使用。一般来说，节点数太多，训练效率不高，可能导致学习时间过长与计算结果不稳定；若节点数过少，很可能导致网络不收敛。本文采用之前工程应用的经验，通过试算隐含层节点数10～30的各个网型，得到最优的隐含层节点数为15。

至此神经网络的结构已经确定完毕，其网型结构为4×15×1。

3.2网络参数的设置

BP神经网络模型的网络参数包括：学习速率ε，平滑因子α，学习误差E，初始权值ω。

平滑因子的引入使得学习速率不再是一个恒定的常数，而是随着迭代误差的改变而调节，因此，需将平滑因子与学习速率综合考虑。通过试算，ε的取值为1.5，α的取值为0.7。

学习误差的大小会对检验中误差造成直接的影响，一般学习误差越小，检验中误差也越小；但是学习误差过小，会导致网络学习速率很慢，甚至不收敛，有时会出现过拟合现象使检验中误差回弹[6]。因此，通过试算建议学习中误差设置为0.01。

初始权值的设置对最终结果的影响十分之大，通常由在固定范围中生成均匀的随机数得到，但是这种方法可能使网络计算过早的进入饱和区。因此，本文利用遗传算法来优化神经网络的初始权值[7]，其具体思想为：对神经网络的连接权重进行编码，形成初始种群，然后以适应度函数指导随机搜索的方向，借助复制、交叉、变异等操作，不断迭代计算，最终产生全局最优解，再经解码得到优化的网络连接的初始权重。

至此用于预测对流层延迟的BP神经网络模型构建完毕。

4融合模型的基本思想

融合模型的实质就是利用BP神经网络算法对霍普菲尔德模型进行误差补偿，即通过BP神经网络模拟出霍普菲尔德模型的误差，将BP神经网络与霍普菲尔德模型融合所得到的模型简称为Hop+BP模型；为了验证霍普菲尔德模型误差的规律性，同时用BP神经网络对多元线性回归进行误差补偿，所得到的模型简称为Mlr+BP模型。两融合模型具体的网型结构如下：

输入层为：测站的海拔高度hs,气压Ps,绝对温度Ts,露点温度td以及霍普菲尔德模型或多元线性回归所求得的对流层延迟δ′；隐含层节点数为15；输出层为霍普菲尔德模型或多元线性回归模型计算结果所对应的残差Δδ′。至此融合模型的神经网络模型建立完毕，其网型结构为5×15×1。融合模型的网络参数设置同BP神经网络模型，在此不再赘述。

需要注意的是，Hop+BP模型所得出的结果是霍普菲尔德模型误差，进行改正时，最终的计算结果是将Hop+BP模型所得的误差值与其对应的霍普菲尔德模型计算值之和。

5工程实例及分析

为了验证融合模型的预测精度，本文选取100个样本的高空气象数据，由文献[8]提供的方法确定测站对流层天顶延迟的理论精确值。其中20个作为学习样本用于建模及神经网络的突触权值训练，剩余的80个样本作为检验样本分别对比多元线性回归、霍普菲尔德模型、BP神经网络以及Hop+BP模型与Mlr+BP模型的预测精度。限于篇幅表1给出了南京站3月17号的部分数据。

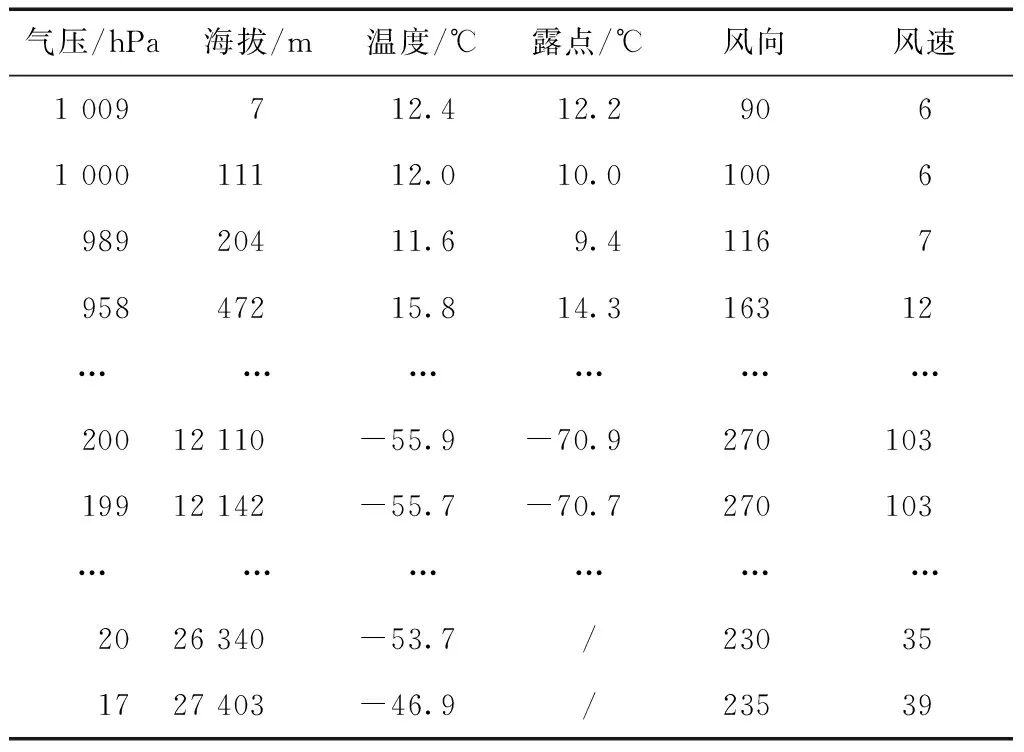
表1　南京站3月17日气象探空数据

5.1多元线性回归的算例分析

由于测站的对流层天顶延迟综合受到海拔高度hs、气压Ps、绝对温度Ts、露点温度td等多方面因素的影响，本文采用一种线性的关系来解释这些自变量与因变量之间的关系，因此,建立多元线性回归模型如式(3)所示。

(3)

式中a0,a1,…,a4等参数可以通过有多余观测的观测值由最小二乘法解算，然后利用回归模型以及地面的气象参数预测对流层延迟。

由回归分析得出模型的学习中误差为3.1cm;检验中误差为2.8cm；a0,a1,…,a4的值如表2所示。

表2　多元线性回归参数值

画出全部100个样本的残差图如图2所示。图中横轴均为样本号，纵轴均为模型残差，其中最左端的20个样本为学习样本。

5.2霍普菲尔德模型的算例分析

霍普菲尔德模型为经验模型，直接得出其预测中误差为22.7cm，画出全部100个样本的残差图如图3所示。

5.3BP神经网络的算例分析

为和多元线性回归模型比较，BP神经网络模型选取与之相同的20个学习样本，剩余的80个作为检验样本，求得学习中误差为2.2cm，检验中误差为2.4cm；画出全部100个样本残差图，如图4所示。

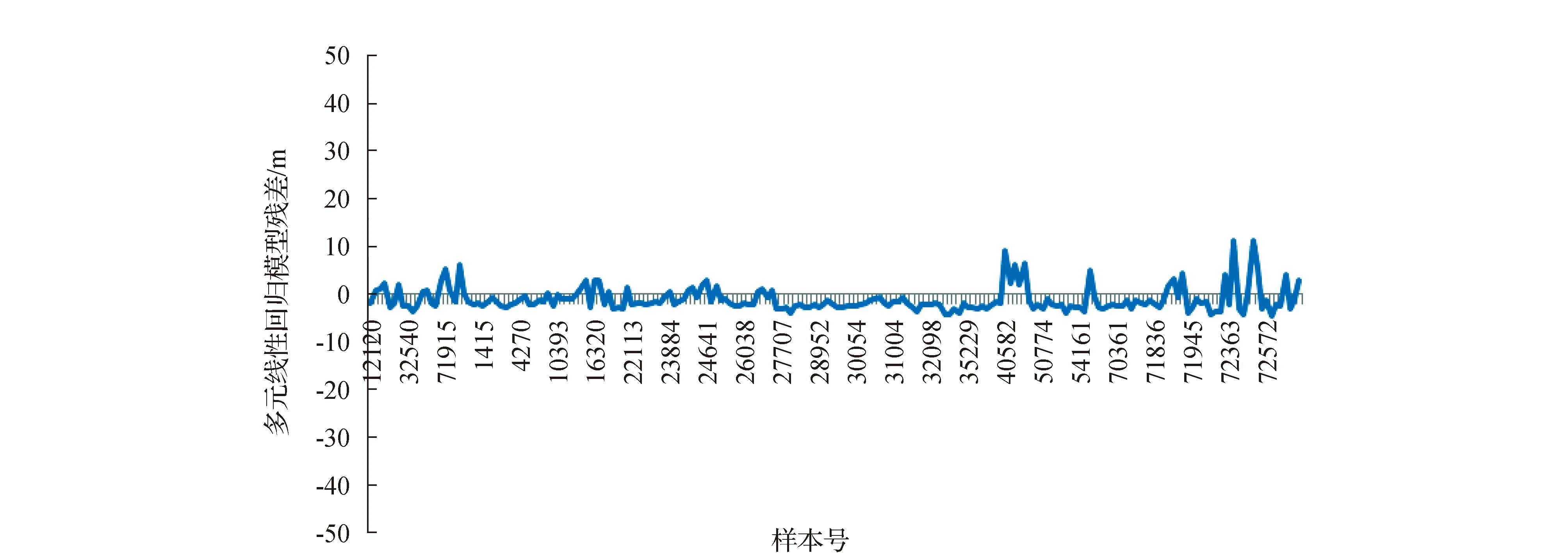
图2　多元线性回归残差

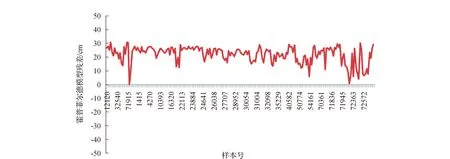
图3　霍普菲尔德模型残差

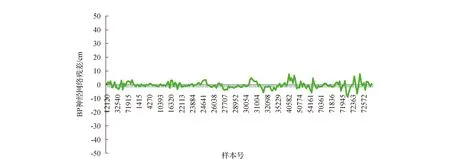
图4　BP神经网络模型残差

5.4Hop+BP模型与Mlr+BP模型算例分析

Mlr+BP模型选取与BP神经网络模型和多元线性回归模型相同的学习样本和检验样本，求得学习中误差为3.1cm，检验中误差为2.6cm。画出全部100个样本的残差图，如图5所示。

为了便于比较，Hop+BP模型选取与Mlr+BP模型相同的学习样本和检验样本，进行神经网络拟合之后，得到学习中误差为0.93cm，检验中误差为1.1cm。画出全部100个样本的残差图，如图6所示。

5.55种模型计算结果对比分析

统计5种模型的检验中误差如表3所示。

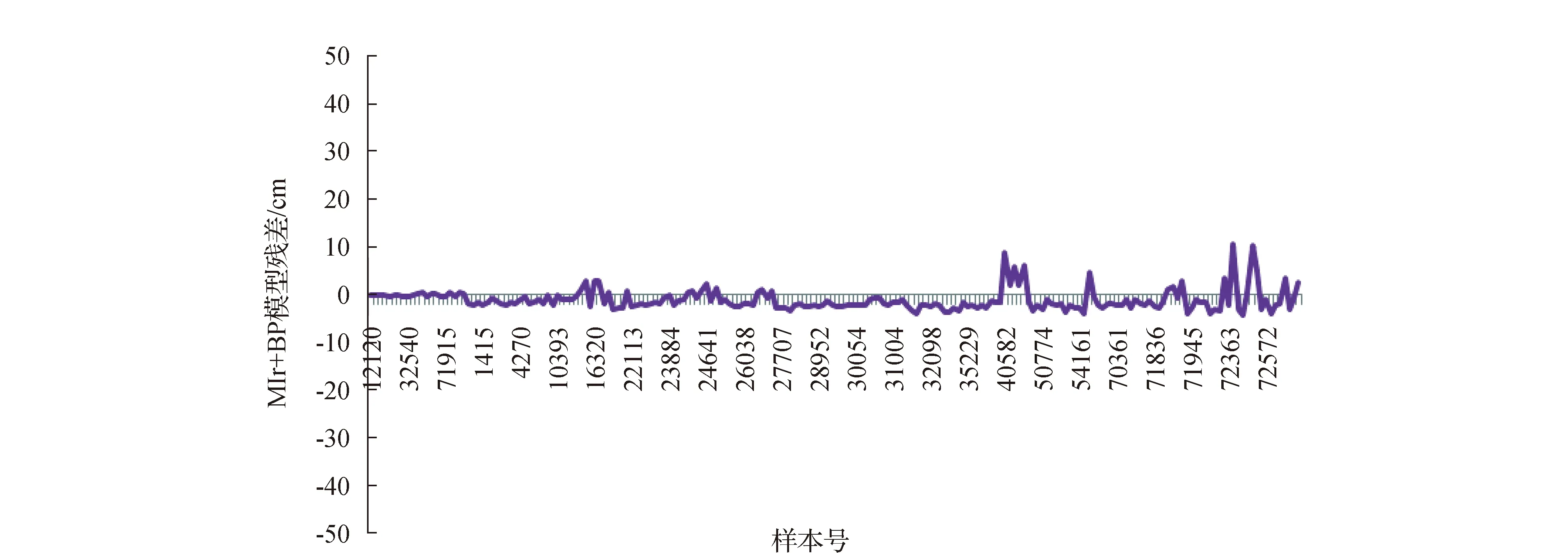
图5　Mlr+BP模型残差

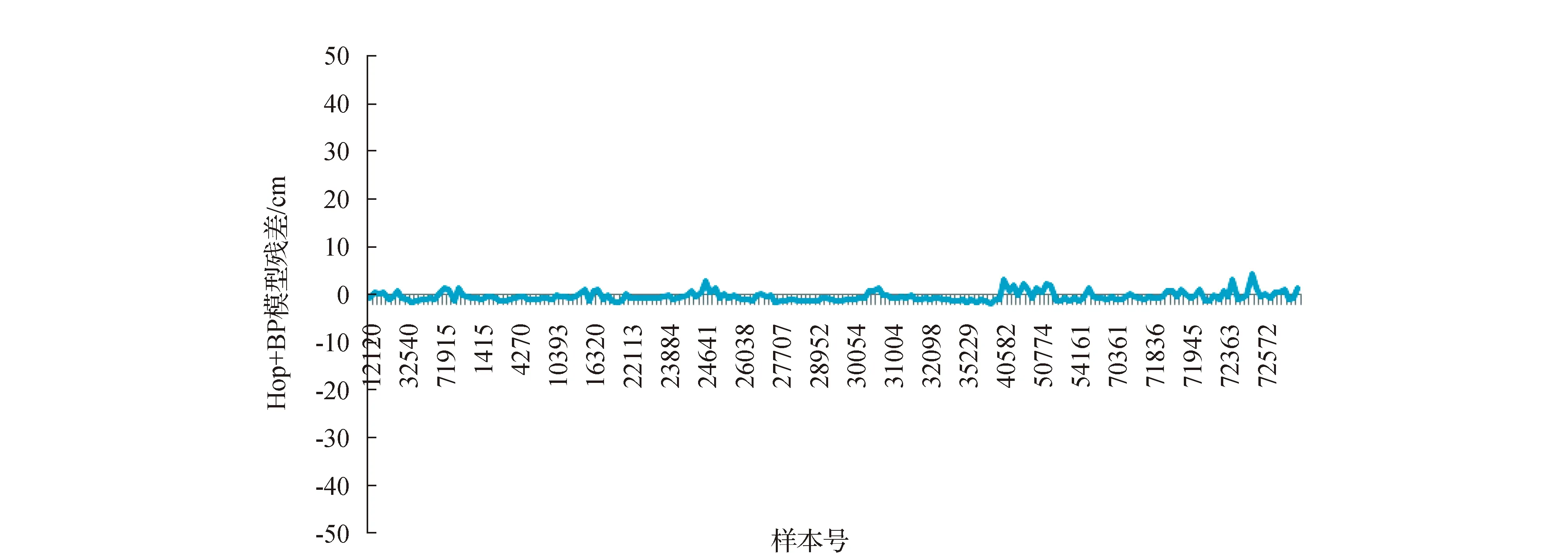
图6　Hop+BP模型残差

cm

由图2和表3可以看出，多元线性回归和Mlr+BP模型的预测精度明显高于霍普菲尔德模型，但是由于缺少合理的物理解释，BP神经网络无法模拟出多元线性回归模型的误差规律，所以Mlr+BP模型的精度较之多元线性回归模型提高有限。同时由图3、图4、图6和表3可以看出，BP神经网络模型的精度亦明显高于霍普菲尔德模型，但是其模型误差并无明显规律，且预测结果不稳定，训练网络所需时间较长，难以满足改正模型实时性的要求。霍普菲尔德模型作为全球使用的普适模型，用于特定的地区误差比较大，这是因为霍普菲尔德模型假设模型中的各个参数随海拔高度的递增服从一定的分布规律，同时假设大气适用理想气体方程，而这种假设和简化相对于区域大气的复杂情况有一定的差异，但是这种差异所导致的误差具有一定的系统性，所以Hop+BP模型利用BP神经网络来模拟霍普菲尔德模型的误差，其精度有着很大的提高，且稳定性良好，神经网络收敛速度快，可以基本满足对流程延迟实时高精度改正的需求。表4给出了5种模型计算对流程延迟误差的最大值和最小值。

表4　5种模型计算误差对比　cm

6结束语

由于对流层所处海拔较低，变化复杂，难以用一个特定的传统模型加以精确描述，本文在分析BP神经网络的原理的基础上，建立了用于改正对流层延迟的神经网络模型；并将之与传统的经验模型相融合，取得了较高的预测精度和稳定的改正结果。同时分析几个模型计算结果中几个偏差较大的样本，都有探空数据首层等压面高程数据缺失的情况，是以第二层等压面的数据代入模型进行计算的，因此出现较大误差。由此可以看出，高程精度对对流层延迟的影响较大。

虽然Hop+BP模型较之传统模型精度有较大的提高，但是其对于气象及高程数据的精度有着很高的依赖，且模型的泛化能力也有待进一步的验证，同时霍普菲尔德模型应用于中国时，其误差的具体规律也有待进一步研究。

参考文献：

[1]高成发，胡伍生.卫星导航定位原理与应用[M].北京：人民交通出版社，2011：232-235.

[2]HAYKIN S.Neural Networks and Learning Machines[M].北京：机械工业出版社，2014：2-14.

[3]HOPFIELD H S.Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J].J.Geophys.Res.1969(74).4487-4499.

[4]欧吉坤.GPS测量的中性大气折射改正的研究[J].测绘学报，1998，27(1)：31-36.

[5]张力仁，徐爱功.GPS定位中的对流层模型分析[J].测绘工程，2009，18(6):33-36.

[6]胡伍生，神经网络原理及其工程应用[M].北京：测绘出版社，2006：68-71.

[7]张帆，胡伍生.神经网络融合模型在大坝安全监控中的应用[J].测绘工程，2015，24(1)：53-56.

[责任编辑：刘文霞]

Improved research for Hopflied model based on BP neural network

ZHU Mingchen1,ZHAO Ping1,CHEN Weirong2

(1.Department of Civil Engineering and Architecture,Tongling University,Tongling 244061,China;2.School of Surveying Engineering Southeast University,Nanjing 210096,China)

Abstract：In order to analyze the law of temporal and spatial variation of troposphere wet delay and promote the amendatory precision of troposphere delay,this paper improves the traditional Hopfield troposphere model to form a new fusion model(Hop+BP model) by the advantage of Back Propagation neural network for solving nonlinear problems.Through comparing the fusion model with traditional Hopfield troposphere model,multiple linear regression model,and Back Propagation neural network model respectively,this paper draws the following conclusion：Hopflied troposphere model has a clear systematic error with a lower precision；multiple linear regression model has a higher precision,but with the nature of mandatory fitting,which lack of physical interpretation thus being difficult for popularization and application；the computational precision of Back Propagation neural network model is 80%,which is higher than Hopfield troposphere model,but has obvious instability；the fusion model embraces the advantages of high precision and stability,and with a deviation of 1.1 centimeter,which is evidently better than traditional methods.

Key words：Hopflied model;BP neural network;multiple linear regression;precision analysis

DOI:10.19349/j.cnki.issn1006-7949.2016.09.006

收稿日期：2015-05-11;修回日期：2015-06-12

作者简介：朱明晨(1988-)，男，助教.

中图分类号：P228

文献标识码：A

文章编号：1006-7949(2016)09-0026-05