基于改进免疫遗传算法的加工工艺重构

徐立云, 刘　伟, 楼科文, 李爱平

(同济大学 现代制造技术研究所，上海 201804)



基于改进免疫遗传算法的加工工艺重构

徐立云, 刘伟, 楼科文, 李爱平

(同济大学 现代制造技术研究所，上海 201804)

摘要：针对产品生命周期内不同阶段市场需求量不同，通过添加或移除相应机床与装夹设备以满足其产能需求变化.针对某产品减产情况，基于抽调原则选择合适生产设备进行移除以适应产能需求；采用一种疫苗自动获取与动态更新的改进免疫遗传算法，通过对相应基因座上基因值的转移调整替代交叉变异算子，从而实现可转移操作在不同工位间的转移，并以瓶颈节拍时间最短和工位间不平衡度最小为目标函数，对原有加工工艺转移重构从而达到新构形下的工艺平衡与优化.最后通过实例分析与对比验证方法的有效性.

关键词：可重构制造系统； 工艺重构； 生产构形； 改进免疫遗传算法

近年来个性化需求不断提高，产品市场需求波动更为频繁，可重构制造系统(reconfigurable manufacturing system, RMS)应运而生.该理念由密西根大学Y. Koren教授[1]首次提出，因其能够快速调整系统生产能力大小与生产功能范围以应对市场的不规则需求，故受到国内外学者的普遍关注.

目前，制造系统重构研究主要集中在2个方面：第一方面是关于机床设备功能模块的增减研究.如文献[2-5]均通过对可重构机床(reconfigurable manufacturing tool, RMT)子模块的增减而提升或降低机床的生产能力.Shbaka等[6]通过对加工特征与机床模块的对应关系来实现不同零件的加工操作的组合.另一方面则是关于系统物理构形的研究，如增添或移除机床、更改物流系统等，从而改变生产线的生产范围与生产能力.如Wang等[7]介绍了添加或移除机床来调整制造单元产能以适应市场需求，并利用改进遗传算法确定系统最经济的重构方式.EIMaraghy[8]和Azab等[9]都提出可重构工艺规划(reconfigurable process planning, RPP)的概念，但其RPP模型均是利用零件族的标准工艺规程建立了面向进化零件族的工序，研究对象是零件族内所增添的新特征与新加工操作，针对这些新内容对原有工艺进行增加或删除部分相关内容.Putnik等[10]对产能缩放的概念进行了详细的论述.楼洪梁等[11-12]应用排队论方法，分别建立了单双零件族随机市场需求模型与RMS的排队模型，结合仓储容量大小研究确定RMS在各需求周期的最优产能.Aguilar等[13]研究在设备选型、混流生产以及随机需求等不同情况下产能的确定.段建国等[14]通过对生产能力缩放性原理的研究，给出了实现产能重构的实现思路.综上所述，现有可重构系统产能方面的研究多集中于可重构机床，对于工艺重构方面的研究则多是针对产品族内出现的新特征与新操作，具体到加工工序方面的工艺重构研究涉及较少.

本文针对市场需求量下降的产品生产线，通过减少设备量改变其生产构形，基于改进免疫遗传算法实现加工工艺的重构，进而快速满足市场生产需求变化.

1问题描述

研究的是具有多个制造单元的发动机缸体生产车间，各制造单元间具有相同类型的生产设备而生产不同型号产品.假设有制造单元a和b如图1所示，单元a所生产的产品量减少，而单元b所生产的产品量增加，此时从单元a中抽调部分机床与夹具设备到单元b，在降低单元a产能的同时又满足了单元b产能提升需求.单元a在特征操作总时间不变前提下，计算新的生产节拍下所需生产设备数量以及可移除数量，在设备抽调原则指导下，对设备进行选取并移除.待所有特征对应的加工操作分类聚类处理后分为固定操作和可转移操作，固定操作固定到指定工位上，而将可转移操作在剩余工位设备上进行转移调整.在瓶颈节拍时间最短与工位间不平衡度最小的综合优化目标下，可转移操作在各工位间不断调整最终达到新的工艺平衡.

a 制造单元a

b 制造单元b

2数学模型的建立

2.1缸体特征分析

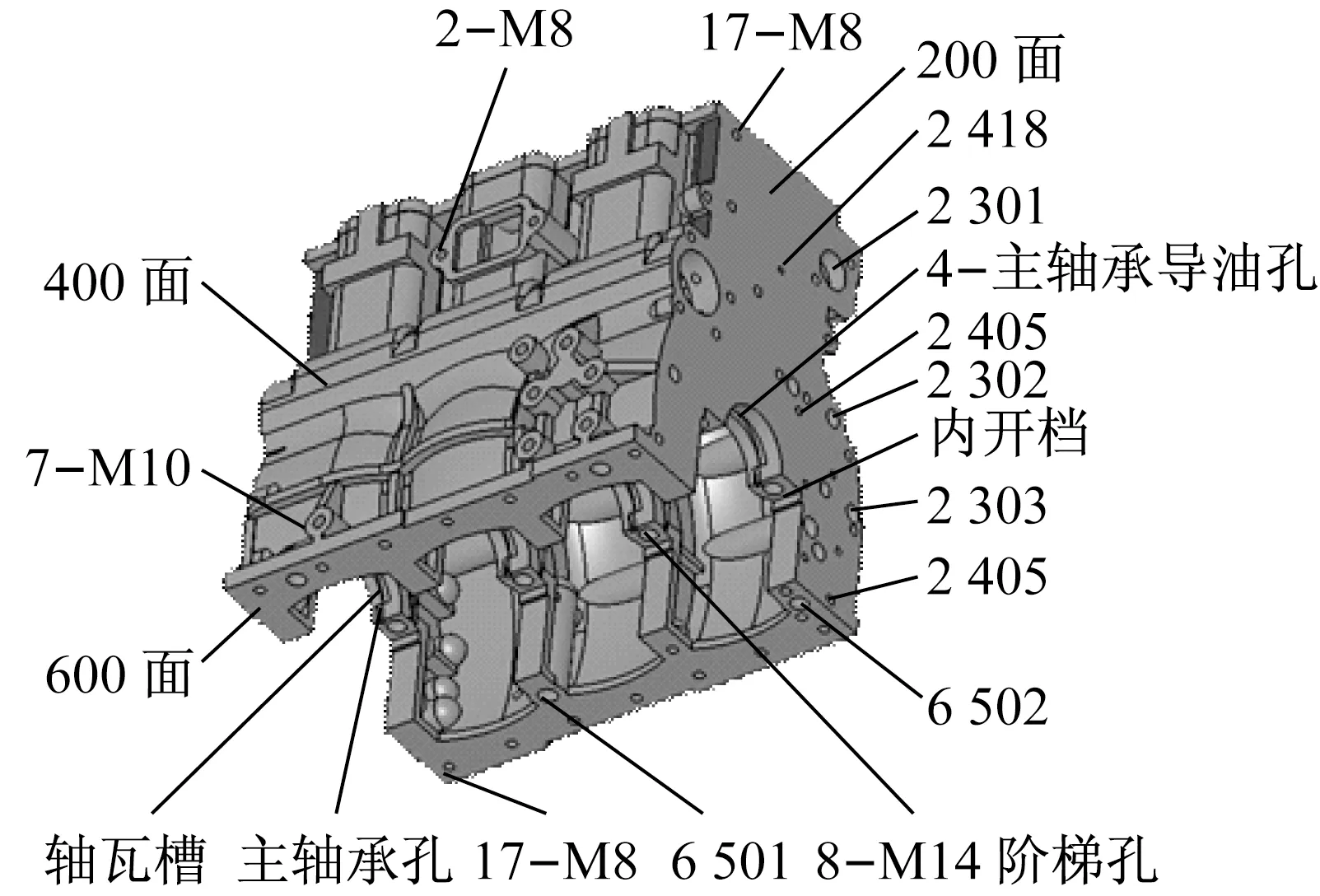
发动机缸体是典型的复杂箱体类零件，主要特征种类有平面、凸轮轴孔、主轴承孔、挺柱孔、定位基准孔、缸(套)孔、螺纹孔、斜油孔、水油道孔、内开档等，缸体零件主要模型如图2所示.不同特征分别对应不同加工方法，主要特征的加工链如表1所示.

a

b

表1　缸体零件主要特征加工链

2.2特征约束

约束是指在工艺实践中的表现为加工先后顺序上的要求，是工艺路线中最重要的要求.必须考虑的几类关系有：①先基准后其他；②先面后孔；③先主后次等.

在特征加工方法和加工工艺参数已知情况下，制造系统的工艺仅需在上述约束下将选定的加工操作重新组合分配至工位上，即可实现加工工艺的重构.在重新分配优化前，需将众多操作进行分类与聚类以减少操作数量，缩小计算规模，提高算法效率.

传统的分类聚类是将缸体特征按其类型、大小不同进行分类，再将完全相同的特征聚合为一个特征.本文在特征聚类基础上对其加工操作进行更进一步的聚类：针对同一特征的加工链，若加工链中的连续操作加工基准相同，则可将该加工链聚类为一个操作.如挺柱孔的扩绞操作均以粗铣后的平面作为加工基准，故在传统聚类后将扩孔与铰孔合并为一个操作；缸套孔的粗镗和半精镗是以粗铣后的平面作为加工基准，故粗镗与半精镗可聚类为一个粗镗操作，而精镗需精铣后的平面作为加工基准，故精镗与聚类后的粗镗不能进行进一步聚类.

待操作聚类完成后，检查每个操作能否在工位j(j=1,2,…,m)的装夹姿态下加工以及其加工基准是否在工位i(1≤i≤j)上已加工完成.将同时满足上述2个要求的加工操作定义为该工位下的可达加工操作，根据操作在各个工位的可加工与否将每个操作的可加工工位用s表示.将传统的前后优先约束关系通过上述操作可达性判断而转换成操作可否在该工位上加工.故在对原有操作进行分类聚类等预处理后可将加工操作信息表示为On=(I,s,o,t)，其中：I为操作编号；s为该操作的可加工工位集，例如操作On的s为2和3，则表示操作On可在第2工位与第3工位上进行加工；o为特征操作内容；t为特征操作加工时间，包括实际加工时间与辅助时间.

2.3数学模型

加工该零件的所有操作总时间(包括辅助时间)为Ttotal；市场新需求下产品订单数量为Dnew；订单Dnew下的需求周期为dp；期望节拍大小为Cexp；生产该零件所需的全部操作为Ototal；固定操作集为Ofix，如加工基准、定位孔以及一些只能在单一装夹姿态下完成的操作；可在不同工位、不同装夹姿态下加工的操作集为可转移操作，用Otrans表示；生产线上机床总量为M；j工位上的机床数Mj；新节拍大小为Cnew；可转移加工操作总数为N；生产线工位集为S(S=1,2，…，i,…，j,…，m，m为工位总数)；j工位实际分配操作加工时间与理论节拍时间的差值为Kj；生产线上各工位间的节拍的不平衡度为U；瓶颈节拍时间为CB；j工位上的所有固定操作时间总和为Tfix(j)；j工位的节拍时间为Cj；算法迭代次数为g.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式(1)计算新订单要求下的期望节拍时间；式(2)计算新的生产任务下所需机床数目，若Ttotal|Cexp，则M=Ttotal/Cexp；式(3)计算新需求下的新节拍值；所有操作间的关系如式(4)所示；式(5)表示操作On的可转移工位集s；式(6)表示任意可转移操作只能分配到其中一个可转移工位上；式(7)表示工位上所分配的操作的总时间不能超过该工位上机床设备所能提供的总加工时间；式(8)用以计算操作分配后工位的实际生产节拍与期望节拍的差值，在分配过程中，若该值大于零，则表示工位上的操作分配过多，超出该工位所能提供的生产能力范围，此时需将该工位标记为待转出工位.反之，则表示该工位上仍能接受新操作，将该工位标记为可转移工位；式(9)为各工位间不平衡度，用以衡量工位间机床的平衡率；式(10)表示瓶颈节拍时间.

目标函数：重构工艺方案的目标为瓶颈节拍时间最短且工位间不平衡度最小，故分别采用瓶颈节拍时间CB与工位间不平衡度U值来衡量，采用统一目标W表示为

(11)

式中：λ为权重系数，通过调节该值可调整在目标函数W中U和CB所占比例的不同.该目标函数中已包含物流搬运的影响，因缩量生产通过移除设备来体现，重构成本可以忽略.

3算法设计

3.1抽调原则的确定

市场需求减少，产能应相应降低，应先完成生产线物理构形的重构，即计算确定要移除的机床数，选取抽调工位后将多余设备从该生产线上移除，然后通过算法完成新构形下的工艺重构.因此，选取移除的机床设备是工艺重构的基础.为尽快完成工艺重构，尽量不涉及太多变动，包括装夹方案应保持不变.具体的抽调原则规定如下.

(1)选择具有并联机床的工位作为移除机床工位，工位上的所有固定加工操作总时间应不大于工位上剩余机床所能提供的加工能力，如式(12)所示：

(12)

式中：q为将被抽调走的机床数.若各工位的固定加工操作时间均没有超过新节拍时间，则进入条件(2)的选择.

(2)选择没有固定加工操作的工位，即该工位上的加工操作均能转移至生产线上其他工位进行加工.如果生产线上各工位均不满足该条件，则进入条件(3)进行选择.

(3)统计各工位的可转移操作数目，选取该数目值最多者作为抽调工位.

3.2改进免疫遗传算法简介

传统遗传算法是一种随机生成后检测满足与否的不断迭代搜索算法，其本质是一种通过目标函数的限制实现定向制导的随机搜索技术.然而，交叉和变异2个算子却是在一定概率下随机地没有指导的迭代搜索[15]，这使得遗传算法收敛速度缓慢，甚至出现退化现象.为了弥补遗传算法的不足，引入生物免疫机制，使用一种有指导性的转移方法替代交叉和变异算子，给出一种基于疫苗自动获取与动态更新的改进免疫遗传算法，利用先验知识构造疫苗，并利用免疫检测实现自我调节，防止算法退化，提高算法收敛效率.

采用改进免疫遗传算法对染色体进行进化操作以实现种群的进化，从而生成更优秀的新种群，不断迭代寻求最优解.主要改进部分的思想是：在下一代种群的生成过程中，要求每次转移都能实现工位间不平衡度的减少，有针对性地实现种群的进化.具体种群更新进化实现步骤如下：

(1)计算各工位K值，分别选定最大与最小K所在工位为转出工位和转移目标工位.

(2)检查转出工位与转移目标工位间有无可转移操作，有则记录所有可转移操作并转至步骤(3)；否则，转至步骤(4).

(3)从可转移操作中随机抽出一个操作进行转移，将操作转移后得到的个体作为中间个体.

(4)保持转出工位不变，剔除已检查的转移目标工位后，选取K最小值所在工位为转移目标工位，转至步骤(2).

加工操作在工位间转移后，各工位的操作集需进行及时更新.该操作集将作为中间种群进行免疫算子操作，经免疫算子操作后选择出新个体组成下一代种群，实现种群的更新.

3.3求解过程

(1)令g=1，将选出的抽调工位作为转出工位，随机生成初始转移方案.每个转移方案由1条染色体表示；创建含有r个疫苗的疫苗库，设其值均为100 000(无穷大值).

(2)根据转移方案，更新各工位的操作集合.

(3)计算Kj(j=1,2,…,m)，U和CB，选定转出工位与转移目标工位.计算各染色体目标函数的适应度值，提取该代解的疫苗并与疫苗库内的疫苗进行比较，将最优的r个疫苗保存下来，实现疫苗库的动态更新.

(4)种群的更新进化.

(5)将得到的中间个体作为父代个体，按比例抽取进行疫苗接种，转至步骤(6).

(6)对接种疫苗的个体进行免疫检测，计算其适应度值，若接种后适应度低于父代个体，则取消接种；否则，接受接种结果.经检测后的个体组成新种群.转至步骤(7).

(7)若g≤gmax，令g=g+1，转至步骤(2)；否则转至步骤(8).

(8)结束.

4案例分析

某柴油机厂发动机缸体生产车间共有4个制造单元,即1，2，3，4，每个单元分别生产一款产品.各单元内均有7台完全相同的四轴加工中心组成粗加工岛；另外共有8台加工中心组成精加工岛.加工车间区域分布如图3所示.

现根据市场需求情况了解到，1号单元生产的缸体正处于成长阶段，产量需求不断增大；而2号单元生产的缸体已处于衰退阶段，产品订单下降.故现计划提高1号单元的产能，而降低2号单元产能.

图3　加工车间示意

2号单元所生产的发动机缸体模型信息如图4所示，加工所需总工时为3 369.9 s，共有5个工位，除工位1为单工位外，其余工位均为并行工位(各2台设备).工厂机床设备1年有270 d进行加工作业，实行两班制，每天工作时间为16 h；原生产纲领为每年40 000台，现计划减产至每年35 000台.各工位的装夹定位方式分别如下：①以底面600面作为粗基准，以缸套孔定位，600面向下.②以左侧面300面为基准，结合两水闷孔进行一面两销定位，300面朝下.③以底面600面作为基准面，一面两销定位.④以前端面200面及其面上两销进行定位，利用工作台旋转加工特殊工位特征——斜孔，精加工600面作为后续工位的精加工基准.⑤以600面为精加工基准，一面两销进行定位.

根据订单需求，计算期望节拍时间为Cexp=3 600×16×270÷35 000=444.34 s，所需设备数M=(3 369.9/444.34)+1=8台，即可从2号制造单元抽调9-8=1台设备转移至1号制造单元，支持1号单元产能提升.则2号单元实际新节拍时间为Cnew=3 369.9÷8≈421.2 s.

原工艺方案整理如表2左侧部分所示，其中黑体表示该操作从原工艺中其他工位上转移而来；×符号表示该操作为固定加工操作，如工位1上加工的水闷孔将作为工位2的定位基准，故其加工操作必须作为固定操作在工位1上.原方案中各工位的固定加工操作的总工时分别为252.13，217.21，0，495.12，624.66 s.根据移除机床选择原则，工位4和工位5必须保证有2台机床以确保固定加工操作能够分配；根据抽调原则(2)，工位3必然选定为抽调工位且为初始解中的转出工位.

b

4.1编码与译码

编码：本文采用实数制编码方式.由表2左侧原有工艺可知，工位1至工位5上总计有5+8+22+6+1=42个可转移操作，故需生成具有42个基因位的染色体.每个基因位上的基因值均从操作的可转移工位s中随机抽取.如图5所示的染色体方案示例，该方案包含原有5个工位的42个可转移操作，其中原工位1的5个可转移操作的初始转移方案是分别转移至工位1、工位4、工位4、工位1和工位2，所以可转移操作的基因值均为各自s中的可转移工位，则可确定该染色体对应的转移方案为可行解.按此方法，随机生成Ps个染色体作为初始种群.

表2　重构前后的工艺方案

(续表2)

图5　染色体示例

译码：译码针对染色体每个基因位上的基因值，通过基因值可找到对应操作转移到的工位号.如图5染色体上第1个基因位上基因值为1，表明该操作将由原工艺方案中的工位1转移至重构方案中的工位1，即保持不变；而第2个基因位的基因值为4，表示该操作将转移至重构方案中的工位4，以此类推，则可得到新工艺方案中各个工位上的所有操作.

4.2免疫算子的执行

(1)疫苗提取.根据目标函数计算种群中每个个体的适应度值，若前5优解中包含1个共同信息e，则可认为包含信息e的解理论上有更多的可能达到最优，故将信息e作为疫苗进行提取并存储于疫苗库内.因每个疫苗都只是利用某一局部信息来探求全局最优解，故应通过迭代算法实现对求解问题的动态疫苗提取，根据每代解的不同情况，将每一代的前5优解中共同信息提取出来作为疫苗，建立动态疫苗库.仅当当前代的前5优解中有比疫苗库中的疫苗适应度高时，则取代疫苗库中的现有疫苗成为新疫苗.

(2)接种疫苗.种群中个体总数为Ps，经转移操作后形成中间种群，设置抽取接种疫苗概率为α，则从中间种群中选择出αPs个个体，对该部分被选中个体进行疫苗接种操作，即将该部分个体的染色体上对应的基因位的基因值更改为记录下来的值.

(3)免疫检测.免疫检测算子是指在种群接种疫苗后计算其适应度值，若接种后的适应度值比接种前的适应度值低，则放弃此次的接种，保持原染色体值不变；反之，则接受.

4.3参数设置

利用Matlab软件进行编程计算，分别设置参数为不同数值，经过多次试验，综合收敛速度和收敛结果后得到各自最佳参数值为：种群大小Ps=40，迭代次数gmax=200，抽取疫苗比例α=5%，权重系数λ=1/40.试验采用计算机配置如下：i5-4200U双核处理器，4G DDR3内存，采用上述参数进行程序寻优时耗时359 s.算法寻优过程如图6所示，求得最优解的工位间不平衡度U=9.29 s，瓶颈工位节拍时间CB=422.35 s.重构工艺方案如表2右侧所示，并在表中列出各操作重构前所在工位号.

图6　IIGA算法寻优

图7为传统遗传算法(GA)与改进免疫遗传算法(IIGA)的收敛情况对比.前者因交叉变异操作的随机盲目性，在第32代解时产生退化现象；而后者可有效避免退化现象，收敛速度更快，结果更优.

图7　GA与IIGA收敛情况

5结语

针对产品生产需求减小的情况，对系统工艺重构进行了研究.通过对加工操作的预处理，将传统先后约束关系转换成操作能否在工位上加工.基于生产线上机床设备选取抽调原则，选取并移除适当的机床设备，构建了系统工位间不平衡度与瓶颈节拍时间最小的综合优化模型，将免疫算子嵌入遗传算法中，并使用转移操作替代交叉变异算子设计改进免疫遗传算法来完成模型求解.该算法不仅继承了遗传算法的强大搜索能力，还结合了疫苗的局部最优性质，使收敛速度加快.最后以某企业的缸体生产线为例，有效地验证了本文所给方法的可行性，可供箱体类零件的工艺规划借鉴.

参考文献:

[1]Koren Y, Heisel U, Jovane F,etal. Reconfigurable manufacturing systems[J]. CIRP Annals-Manufacturing Technology, 1999, 48(2): 527.

[2]Landers R G, Min B K, Koren Y. Reconfigurable machine tools[J]. CIRP Annals-Manufacturing Technology, 2001, 50(1): 269.

[3]Spicer P, Koren Y, Shpitalni M,etal. Design principles for machining system configurations[J]. CIRP Annals-Manufacturing Technology, 2002, 51(1): 275.

[4]Goyal K K, Jain P K, Jain M. Multiple objective optimization of reconfigurable manufacturing system[C]∥ Proceedings of the International Conference on Soft Computing for Problem Solving. Roorkee: Springer India, 2012:453-460.

[5]Goyal K K, Jain P K, Jain M. A novel methodology to measure the responsiveness of RMTs in reconfigurable manufacturing system[J]. Journal of Manufacturing Systems, 2013, 32(4):724.

[6]Shabaka A I, ElMaraghy H A. A model for generating optimal process plans in RMS[J]. International Journal of Computer Integrated Manufacturing, 2008, 21(2): 180.

[7]Wang W, Koren Y. Scalability planning for reconfigurable manufacturing systems[J]. Journal of Manufacturing Systems, 2012, 31(2): 83.

[8]ElMaraghy H A. Reconfigurable process plans for responsive manufacturing systems[C]∥Digital Enterprise Technology. Boston: Springer US, 2007:35-44.

[9]Azab A, ElMaraghy H A. Mathematical modeling for reconfigurable process planning[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1): 467.

[10]Putnik G, Sluga A, Elmaraghy H,etal. Scalability in manufacturing systems design and operation: State-of-the-art and future developments roadmap[J]. CIRP Annals-Manufacturing Technology, 2013, 62(2):751.

[11]楼洪梁, 杨将新, 林亚福,等. 单零件族可重构制造系统的生产能力优化设计[J]. 农业机械学报, 2007, 38(2):125.

LOU Hongliang, YANG Jiangxin, LIN Yafu,etal. Optimal capacity design of reconfigurable manufacturing system for single part family[J]. Transactions of the Chinese Society for

Agricultural Machinery, 2007, 38(2):125.

[12]楼洪梁, 杨将新, 林亚福,等. 双零件族随机环境下可重构制造系统的生产能力设计[J]. 计算机集成制造系统, 2007, 13(1):13.

LOU Hongliang, YANG Jiangxin, LIN Yafu,etal. Capacity design of RMS for double product families under stochastic demand[J].Computer Integrated Manufacturing Systems, 2007, 13(1):13.

[13]Aguilar A, Roman-Flores A, Huegel J C. Design, refinement, implementation and prototype testing of a reconfigurable lathe-mill[J]. Journal of Manufacturing Systems, 2013, 32(2):364.

[14]段建国, 李爱平, 谢楠,等. 可重构制造系统生产能力扩展性重构方法[J]. 同济大学学报：自然科学版, 2012, 40(9):1357.

DUAN Jianguo, LI Aiping, XIE Nan,etal. Reconfiguration method on production capacity expansion in RMS [J].Journal of Tongji University: Natural Science, 2012, 40(9):1357.

[15]韩学东, 洪炳熔, 孟伟. 基于疫苗自动获取与更新的免疫遗传算法[J]. 计算机研究与发展, 2005, 42(5): 740.

HAN Xuedong, HONG Bingrong, MENG Wei. An immune genetic algorithm based on vaccine autonomous obtaining and updating[J]. Journal of Computer Research and Development, 2005, 42(5): 740.

收稿日期：2015-06-29

基金项目：上海市科技创新行动计划(15111105502)；上海市经信委产学研项目(沪CXY-2013-31).

中图分类号：TH162

文献标志码：A

Reconfigurable Process Planning Based on Improved Immune Genetic Algorithm

XU Liyun, LIU Wei, LOU Kewen, LI Aiping

(Institute of Advanced Manufacturing Technology, Tongji University, Shanghai 201804, China)

Abstract：According to the demand changes from the competitive market, machine tools and other resources could be added or removed from manufacturing or assembling lines to meet different outputs. In the case of production reduction, appropriate equipment were selected and removed to change the capacity of the existing manufacturing line based on the removing principle. An improved immune genetic algorithm based on vaccine autonomous obtaining and updating was proposed, crossover and mutation operation in traditional genetic algorithm were changed to transfer and adjustment between different gene locations and transfer of operations between different stations can be realized. The objectives of reconfigurable process planning was to minimize the bottleneck cycle time and imbalance among stations. Finally, a cylinder block case was illustrated to verify the effectiveness of the given method.

Key words：reconfigurable manufacturing system； reconfigurable process planning； configuration; improved immune genetic algorithm

第一作者： 徐立云(1973—)，男，教授,博士生导师，工学博士，主要研究方向为智能制造、系统建模与优化、产品数字化设计与管理等.

E-mail：Lyxu@tongji.edu.cn