基于最大相似度的伪随机交织器盲识别方法
2016-07-22彭贻云杨晓静
彭贻云,张 玉,杨晓静
(解放军电子工程学院,安徽 合肥 230037)
基于最大相似度的伪随机交织器盲识别方法
彭贻云,张玉,杨晓静
(解放军电子工程学院,安徽 合肥 230037)
摘要:针对存在误码时伪随机交织器的识别问题,提出基于最大相似度的伪随机交织器盲识别方法。该方法在得到交织器长度的前提下,对交织器的置换关系进行识别。通过对交织前后的码字序列进行相应的对比,统计出对应码序列的相似度值,找出最大相似度值的位置,从而得出交织置换关系,完成对伪随机交织器的识别。仿真结果表明,本文识别算法在误码率为0.05,接收得到的码组个数大于交织器的长度时,识别准确率可以达到90%以上,具有较好的容错性能。
关键词:伪随机交织器;Turbo码;最大相似度;盲识别
0引言
在现代数字通信系统中,Turbo码凭借其接近香农极限的优异性能得到广泛的应用,针对Turbo码的识别研究也显得越来越迫切。伪随机交织器作为Turbo码编码构造中的重要组成部分,要完成对Turbo码的识别,不可避免要先得到交织器的参数,即完成对伪随机交织器的识别。
目前,关于Turbo码中伪随机交织器的识别研究较少,主要有:Cluzeau M提出一种基于多样本数据的识别算法[1],利用Turbo码编码中信息序列和交织后序列的编码序列对交织器逐位进行恢复,通过设定门限对候选的方案进行排除,得到最终的交织置换关系;Cote M等人提出的基于多样本的一阶相关统计的识别算法[2],利用分量编码器的构造特点,结合交织置换关系逐位进行恢复;张永光根据Turbo码编码的特点,对Turbo码子码识别,得出交织长度和起点等参数,再运用一阶相关统计方法实现了交织关系的识别[3],但只针对无误码的情况。本文针对上述问题,提出了基于最大相似度的伪随机交织器盲识别方法。
1伪随机交织器原理
在Turbo码中,交织器不仅可以抵抗信道产生的突发错误,将信道中连续错误转变成随机错误,还可以提高码字的输出重量,改善码字的距离特性,提高系统性能[4]。交织器又可分为分组交织器、卷积交织器和伪随机交织器[5]。目前,为了得到优异的Turbo码性能和便于工程上实践,其编码构造广泛应用的是伪随机交织器[6-7]。
交织就是对信息序列按照一定的规则重新排列得到交织序列的过程[8]。设交织器的输入信息序列为
u=(u1,u2,…,uN)
(1)其中,uk∈{0,1},k=1,2,…,N,N为交织器的长度。
令交织置换关系为π=(π(1),π(2),…,π(N))(π(i)∈{1,2,…,N}∀i=1,2,…,N,且有π(i)≠π(j),∀i≠j)。按照上述的置换关系对输入信息序列进行交织处理,得到交织后的输出序列
uπ=(uπ(1),uπ(2),…,uπ(N))
(2)
其中uπ(k)∈{0,1},k=1,2,…,N,序列uπ是将序列u中元素按照π的置换关系进行重新排列,两个序列中包含相同的元素。
此时,可以将输入和输出序列表示成如下关系
uπ=u·S
(3)其中,S为N×N的交织矩阵,它的每行元素有且仅有一个1,而且每行元素1的位置都不相同,其余元素为0。
例如,对一个长度为7的伪随机交织器,交织置换关系为π=(2,5,1,7,3,6,4),输入序列向量为u=(u1,u2,…,u7),经过交织器输出得到序列uπ=(u2,u5,u1,u7,u3,u6,u4),按照公式(3)得到其交织矩阵

由交织矩阵可以看出,当S(i,j)=1时,表示交织器将输入序列u的第i个元素映射到输出序列uπ的第j个元素,对于交织置换矩阵π中元素有j=π(i),i=1,2,…,N。
2基于最大相似度的算法实现
本文中对伪随机交织器的识别主要是作为Turbo码识别研究中的一部分,通过对Turbo码编码结构进行分析,得出其中交织器识别的相关条件。
2.1接收编码结构分析
Turbo码通常采用的是并行级联卷积码结构,其编码结构如图1所示。它主要是由两个递归系统卷积编码器并行级联而成,卷积编码器之间用交织器相连。
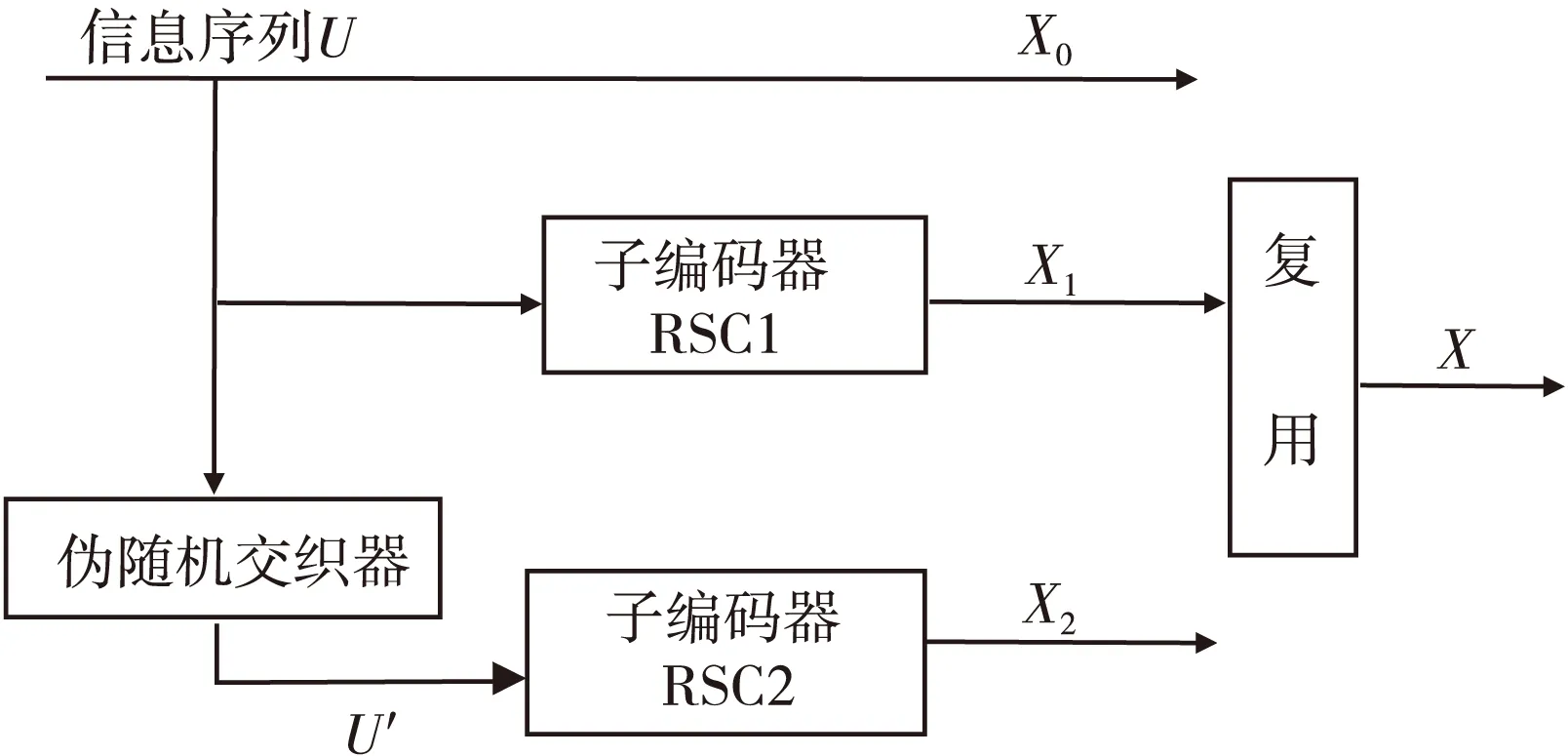
图1 并行级联卷积码结构Fig.1 The structure of parallelconcatenated convolution code
在Turbo码的识别研究当中,对Turbo码的3路复用序列都可以通过接收到的码序列分离得到。此时,交织器的输入和输出序列可以通过分离出的复用序列求出。
由此得到的交织器输入、输出序列,分别按照一定的规格构造相对应的编码矩阵C、Cπ:
(4)
(5)
其中,m为得到的码组个数(为了得到准确的估计值,m应满足条件2m≥N)。
将式(4)(5)带入公式(3)可以得到接收到的编码矩阵的对应方程:
Cπ=C·S
(6)
根据公式(6)可以看出,接收得到的编码矩阵Cπ、C的列向量存在相对应的置换关系。当不存在误码的情况时,Cπ中的每个列向量是C中列向量位置的置换,通过将每个Cπ中的列向量与C中列向量进行遍历对比,可以得到交织置换矩阵S,完成交织关系的识别。
2.2误码条件下的算法实现
考虑到误码的情况,两个编码矩阵中的列向量不存在完全的对等关系,引入相似度的概念。将两个列向量之间的相似度d定义为向量之间对应位置元素相同的个数。相似度数值越大,表明两个向量越接近,存在对等的关系越大。
依次选取C中每个列向量分别与Cπ中的各个列向量进行对比,得到其对应相似度值的大小。将C中每个列向量所对应的相似度值取最大,最大相似度值位置即为所求的置换位置。具体步骤如下:
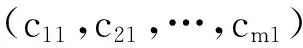
2)求出相似度值序列中最大值的位置,即对应交织矩阵S中第一组列向量中元素1的位置;
3)重复上面的步骤,依次对C中的其余列向量进行处理,得出其最大相似度值得位置,从而求出交织矩阵S的大小,完成对伪随机交织器的置换关系的识别。
综上,通过得到交织器输入输出的编码矩阵,利用最大相似度的方法,可以求出交织器的交织置换关系,而且对于存在误码的情况同样具有一定的识别效果。
3仿真实验分析
根据本文的最大相似度方法对伪随机交织器进行识别仿真,验证该方法对伪随机交织识别的可行性,再通过对误码率与识别效果进行研究,设置不同误码率条件下的伪随机交织器进行识别。
3.1算法验证
对仿真实验的条件进行设置,假设接收得到码组数为30,对于得到的码字序列误码率为0.05。为便于对本文算法进行验证,假设交织器长度为15,交织置换关系为π=[5,8,1,15,10,2,11,6,14,7,4,12,9,13,3]。按照上述的交织置换关系对输入的信息序列进行交织处理,得到交织后的码字序列,对输入、输出的接收序列按照一定规则构成相应的码字矩阵C、Cπ。
假设已知得到了交织器的长度以及交织的初始位置信息,只需对交织置换关系进行识别分析。按照第2章的算法对接收到的编码矩阵进行分析,得到相应列的相似度大小。
先对C中的第一个列向量进行分析,依次将其与Cπ中的各个列向量进行相似度处理,得到一组相似度序列[21 19 14 14 29 18 12 20 14 19 9 15 18 14 11]。求取相似度序列的最大值,得到最大值对应的位置,此时得到最大相似度值为29,其对应位置为5。
依次对矩阵C中其余列向量求取相应的相似度序列,得到表1数据。
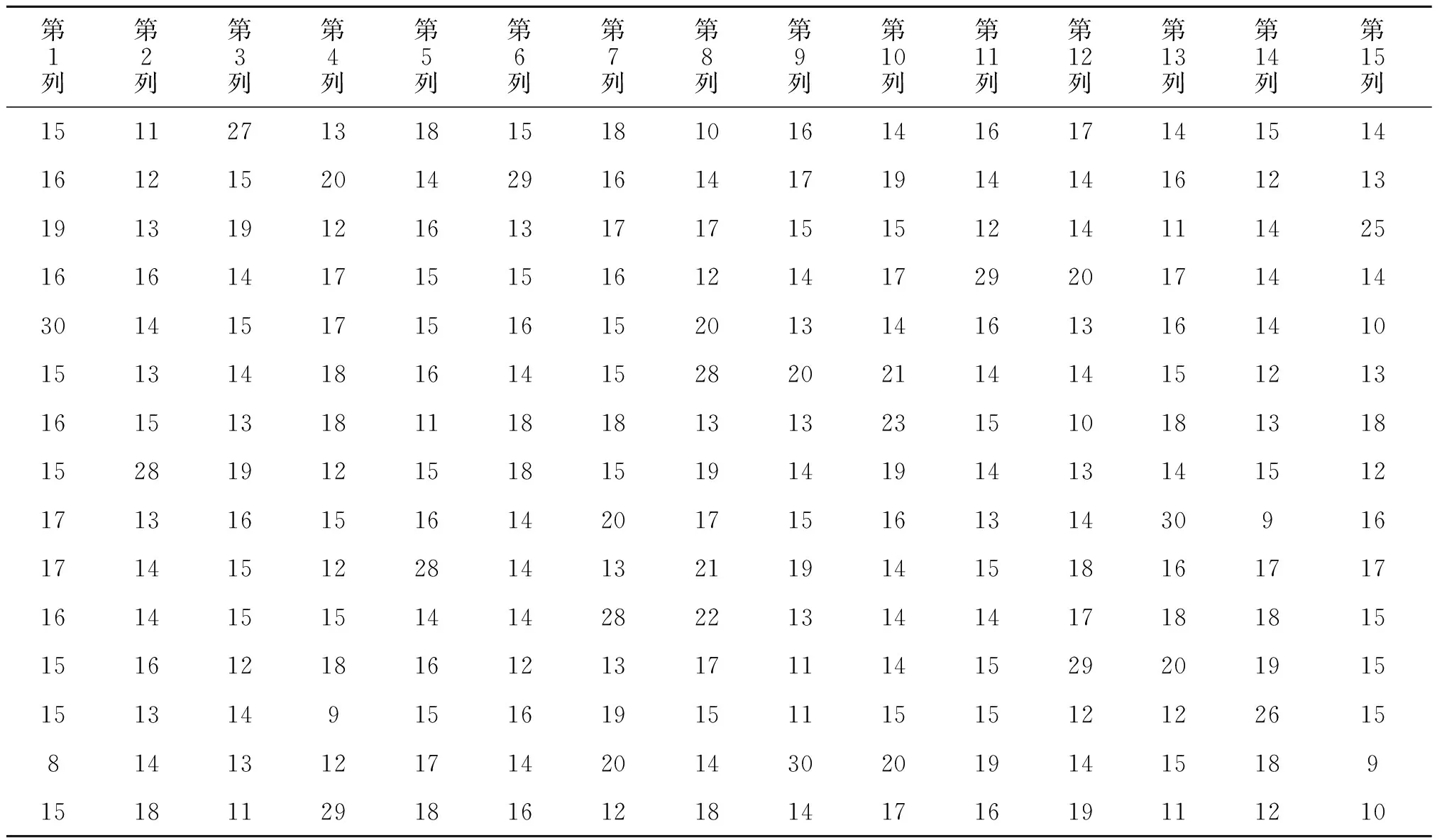
表1 输入矩阵列向量对应的相似度值
通过对表1的数据进行分析,求出每行数据中最大值的位置,即得到对于置换序列π′=[5,8,1,15,10,2,11,6,14,7,4,12,9,13,3],此时完成对伪随机交织器的置换关系识别。
3.2识别性能分析
在对伪随机交织器识别中,由于误码的存在,使得接收到的数据存在一定的偏差,导致识别的结果可能引起错误。通过选取不同的码组个数和设置不同误码率条件,对算法性能进行分析。
为便于体现效果,仅对输入编码矩阵的第一组列向量的置换位置进行识别分析。在选取不同的码字个数条件下,通过1 000次蒙特卡洛仿真实验统计对应的识别成功概率,得到误码率与识别概率的关系如图2所示。
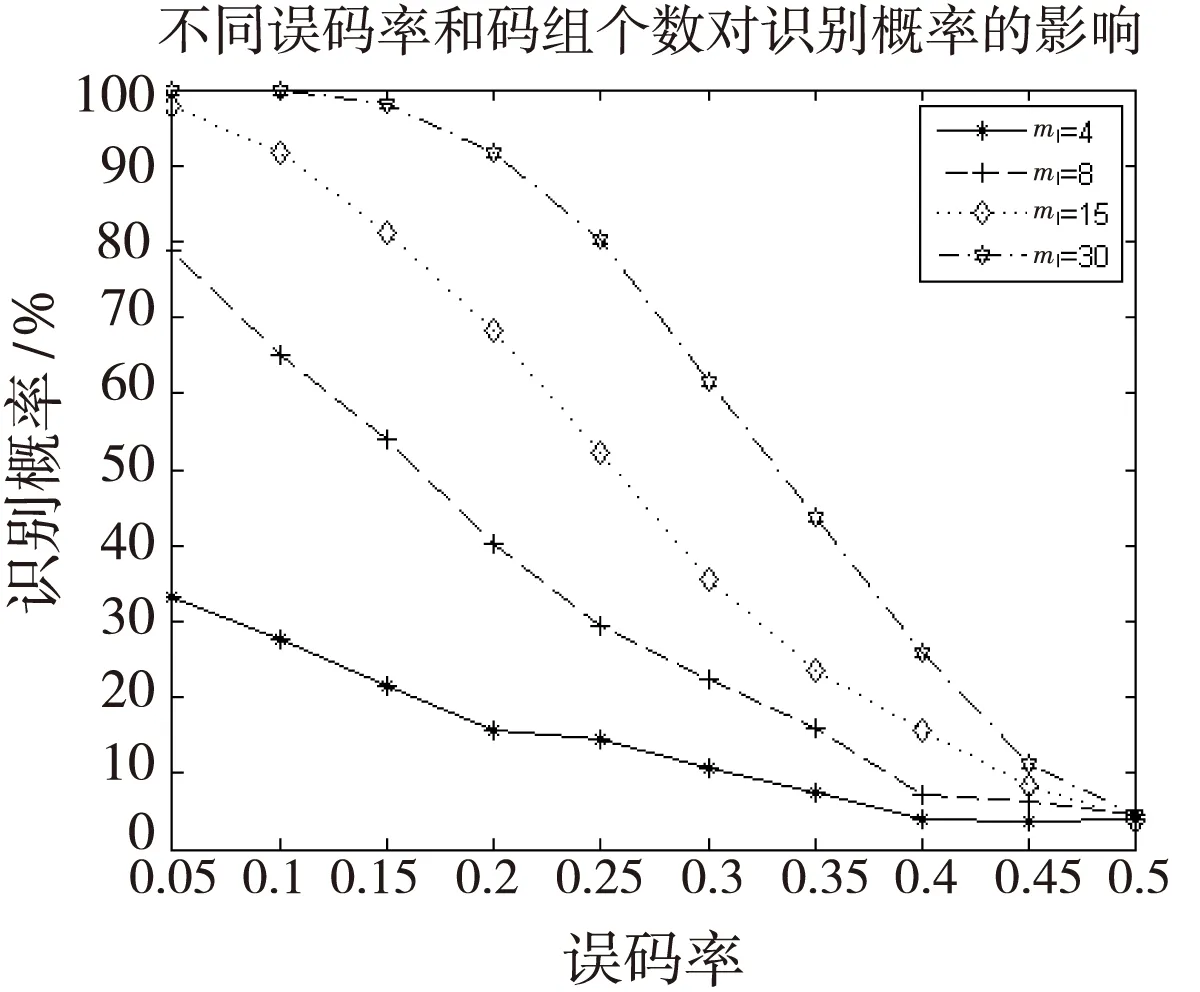
图2 识别概率对比图Fig.2 The constast figure of identification probability
根据图2中的仿真结果可以看出,随着利用的接收码组个数越多,识别的概率也越大。当误码率低于0.05,运用接收得到的码组个数大于交织器的长度时,识别概率可以达到90%以上。通过增加接收得到的码组个数,可以有效地对置换关系进行识别。
4结论
本文提出了基于最大相似度的伪随机交织器盲识别方法。通过对所述算法进行仿真实验,验证了算法的可行性,同时对识别概率的影响因子进行分析。仿真结果表明,在误码率为0.05,接收得到的码组个数大于交织器的长度时,识别准确率可以达到90%以上。通过完成对伪随机交织器置换关系的识别研究,对下一步Turbo码的盲识别研究具有重要意义。
参考文献:
[1]MathieuCluzeau,MatthieuFiniasz,Jean-PierreTillich.MethodsfortheReconstructionofParallelTurboCodes[C]//InternationalSymposiumonInformationTheory2010.Austin,Texas,USA:IEEEPress,2010:2008-2012.
[2]MaximeCote,NicolasSendrier.Reconstructionofaturbo-codeinterleaverfromnoisyobservation[C]//ISIT2010.Austin,Texas,USA:IEEEPress,2010:2003-2007.
[3]张永光.一种Turbo码编码参数的盲识别方法[J].西安电子科技大学学报,2011,38(2):167-172.
[4]AliNaseri,OmidAzmoon,SamadFazeli.BlindrecognitionalgorithmofTurbocodesforcommunicationintelligencesystem[J].InternationalJournalofComputerScienceIssues,2011,8(6):68-72.
[5]张伟杰,张玉.Turbo码中伪随机交织器盲识别方法[J].微型机与应用,2010,29(17):65-70.
[6]解辉,黄知涛,王丰华.信道编码盲识别技术研究进展[J].电子学报,2013,41(6):1166-1176.
[7]于沛东,李静,彭华.一种利用软判决的信道编码识别新算法[J].电子学报,2013,41(2):301-306.
[8]阐剑,易正红,石荣,等.误码条件下Turbo码编码参数的盲识别[J].电子信息对抗技术,2014,29(3):13-16.
*收稿日期:2015-12-30
基金项目:国家自然科学基金项目资助(61201379);安徽省自然科学基金资助项目(1208085QF103)
作者简介:彭贻云(1992—),男,江西泰和人,硕士研究生,研究方向:信号与信息处理,通信信号分析。E-mail:pengyiyun92@163.com。
中图分类号:TP309
文献标志码:A
文章编号:1008-1194(2016)03-0109-04
Pseudo-random Interleaver Blind Recognition Method Based on Maximum Likelihood
PENG Yiyun, ZHANG Yu, YANG Xiaojing
(Electronic Engineering Institute of PLA, Hefei 230037, China)
Abstract:For the problem of blind recognition for pseudo-random interleaver at the error code condition, a recognition method based on maximum likelihood was proposed. After obtaining the length of interleaver, we could recognise the commutative relation of interleaver. Compared with the code sequence before and after interleaved, we accounted the value of likelihood, and found the location of the maximum value. Then we got the commutative relation of interleaver and achieved the recognition of the pseudo-random interleaver. Simulation results showed when the error rate was 0.05 and the received number of code group was larger than the length of the interleaver, the accuracy of the recognition was above 90%.
Key words:pseudo-random interleaver; turbo code; maximum likelihood; blind recognition
