高速机动目标信号多普勒频移补偿方法
2016-07-22董鹏曙谢幼才金加根
董鹏曙,向 龙,谢幼才,金加根
(空军预警学院,湖北 武汉 430019)
高速机动目标信号多普勒频移补偿方法
董鹏曙,向龙,谢幼才,金加根
(空军预警学院,湖北 武汉 430019)
摘要:针对高速机动目标多普勒频率展宽引起的相参积累散焦损失等问题,提出了易于工程实现的目标回波信号预处理方法。该方法构建了多普勒频移变化与加速度、角速度的关系模型。理论分析和仿真表明:在动目标检测(MTD)中相参积累散焦损失由多普勒频移变化率等多个因素所决定,其大小在-20lgN dB至0 dB之间(N为相参积累的脉冲数)。通过提出的多普勒频移补偿方法,可有效消除多普勒频率展宽对MTD相参积累的影响,提高雷达在复杂杂波背景中对高速机动目标的检测能力。
关键词:高速机动目标;运动补偿;检测;多普勒频移变化率
0引言
动目标检测(MTD)通过多普勒滤波实现相参积累,有效提高了目标回波的信杂比,增强了雷达在复杂杂波背景中探测运动目标的能力[1-2]。MTD完成多普勒滤波、实现相参积累的前提条件是在相参处理间隔期内目标运动速度恒定(或变化很小),多普勒频移相同,位于同一多普勒通道。一般情况下,这一前提条件是成立的,因此MTD能够在复杂杂波背景中检测运动目标。但是,对高速机动目标而言,在相参处理间隔期内目标运动速度变化较大,多普勒频移发生显著变化,分布在多个多普勒通道之中。在这种情况下,MTD处理无法有效完成多普勒滤波、相参积累和目标检测[3-5],必须寻找新的处理方法,来完成复杂杂波背景中高速机动目标的检测。
针对高速目标的雷达探测问题,国内外学者开展了广泛的研究,目前主要集中于两类。一类是针对多普勒频率展宽的,先从回波数据估计出目标的运动速度、加速度、加加速度等参数,再补偿回波中的高速运动成分,其方法主要有自相关运动参数估计[4]、单帧回波分段处理[6]、修正离散Chirp-Fourier变换[7]、距离-慢时间域Radon变换[8]等方法。另一类则是针对长时间积累引起的距离徙动以及距离向与方位向耦合问题的,通过变换的方式补偿高速运动导致的散射点的位移,常见的变换有Keystone变换[9]、Radon-Fourier变换[10]等方法。这些方法需要较多回波数据,且计算量大。而对于边扫描边跟踪体制的窄带常规警戒雷达的高速机动目标检测问题则未见有文献研究。本文针对上述问题,提出了高速机动目标信号多普勒频移补偿方法。
1高速机动目标的多普勒频移
对于边扫描边跟踪体制的窄带常规警戒雷达而言,由于脉冲回波个数少,相参积累时间短,距离徙动问题可以忽略,影响相参处理效果的主要因素是高速机动目标的多普勒频率展宽。
高速机动目标瞬时多普勒频移可表示为:
(1)
式中,v(t)为目标瞬时运动速度;θ(t)为目标运动方向与雷达视线之间的夹角;λ为发射信号的波长。由式(1)可知,瞬时多普勒频移fd(t)的变化为:
(2)
将式(2)变形可得:
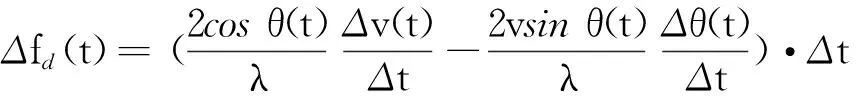
(3)
式(3)中,v′(t)为目标运动速度变化率,即加速度;θ′(t)为目标视角变化率,即角速度。考虑极限值,则有:
(4)
将加速度引起的回波多普勒频移变化记为Δfd(v),角速度引起的回波多普勒频移变化记为Δfd(θ),即
(5)
(6)
1.1加速度对多普勒频移变化的影响
以16点MTD为例进行分析,假设雷达重复频率为250Hz,则相参积累时间Δt为64ms,多普勒分辨单元为15.625Hz;现代飞行器飞行加速度v′可达10 g[6]。表1给出了目标飞行加速度v′为1~10 g、雷达发射频率从VHF频段到X频段时,一个相参处理间隔期内目标回波多普勒频移变化情况(取g=10m/s2)。
由表1可见,仅VHF波段,相参处理间隔期内多普勒频移变化Δf在多普勒分辨单元以内;对P波段,加速度6 g以上时,多普勒频移变化Δf超出一个多普勒分辨单元;对L波段,加速度3 g以上时,多普勒频移变化Δf超出一个多普勒分辨单元;对S及以上波段,加速度1 g以上时,多普勒频移变化Δf均超出一个多普勒分辨单元;即出现跨多普勒通道现象。
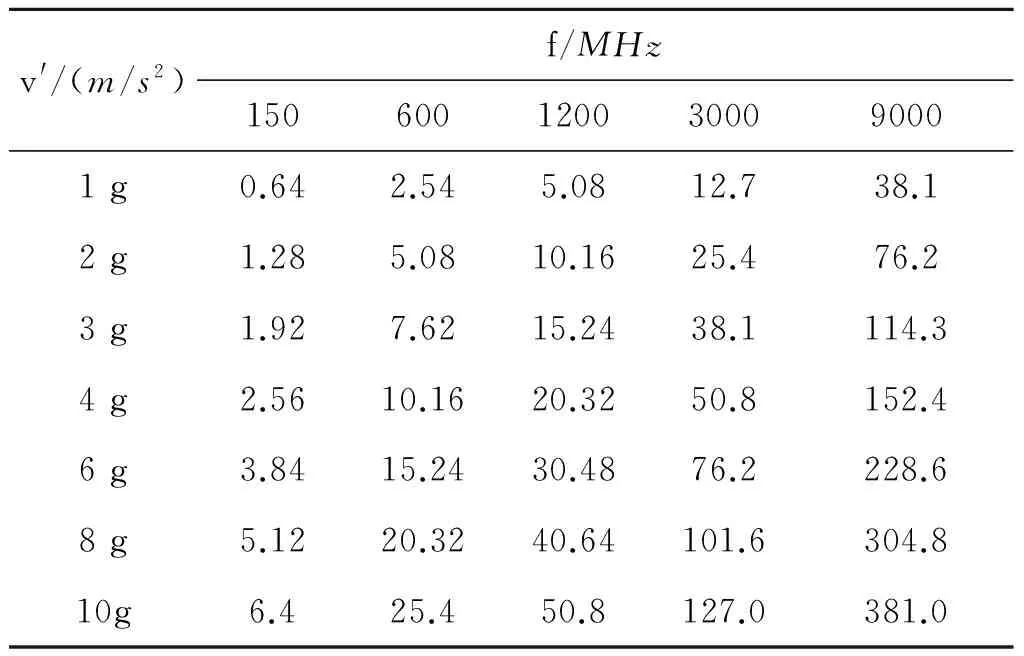
表1 加速度对多普勒频移变化的影响(Hz)
1.2角速度对多普勒频移变化的影响
情报雷达天线转速一般为3~6r/min,角速度为0.314~0.628rad/s;现代飞机机动飞行时转弯角速度可达0.698~1.047rad/s,飞行速度可达数马赫[6]。取目标飞行速度为1 Ma(340m/s),表2给出了总的角速度θ′为0.174~1.047rad/s、雷达发射频率从VHF频段到X频段时,一个相参处理间隔(64ms)期内目标回波多普勒频移变化情况。
由表2可见,仅VHF波段、总的角速度在0.524rad/s以下时,相参处理间隔期内多普勒频移变化Δf在多普勒分辨单元以内;其他情况下,相参处理间隔期内多普勒频移变化Δf均超出一个多普勒分辨单元,出现跨多普勒通道现象。
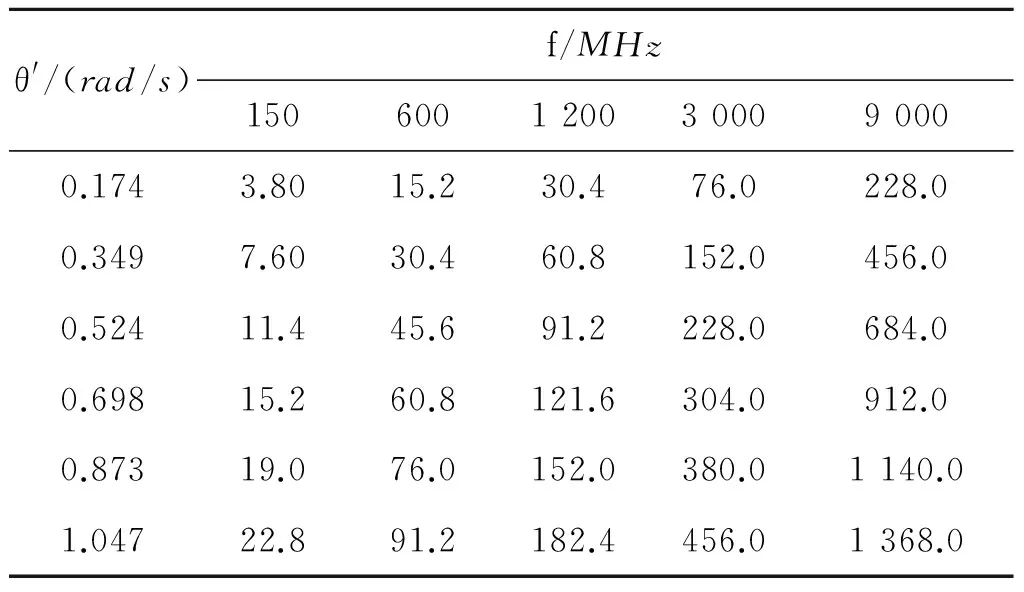
表2 角速度对多普勒频移变化的影响(Hz)
综合考虑目标飞行加速度、角速度对多普勒频移变化的影响,加速度、角速度分别为1 g、0.524rad/s以上时,对各频段雷达而言,相参处理间隔期内多普勒频移变化均超出多普勒分辨单元,出现跨多普勒通道现象。而且雷达工作频率越高,加速度、角速度越大,相参积累时间越长,跨多普勒通道现象越严重。为了保证MTD的性能,必须在信号处理之前对高速机动目标回波进行相应的预处理。
2目标回波信号预处理与仿真
对高速机动目标回波信号进行预处理的基本方法是运动补偿。通过运动补偿,消除相参处理间隔期内的多普勒频移的影响,使信号能量聚集在一个多普勒分辨单元之内。
2.1目标回波信号预处理方法
假设雷达重复周期为T,将相参处理间隔期内的N点回波信号记为S:
S=[s(0),s(1),s(2),…,s(n),…,s(N-1)],
(0≤n≤N-1)
考察复信号s(n),有
(8)
(9)
I(n-1)-jQ(n-1)
(10)
s(n)s*(n-1)=A2exp(j2πfdnT)=
I(n)I(n-1)+Q(n)Q(n-1)+
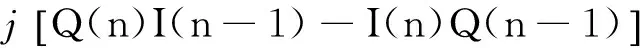
(11)
(12)
由此可得相参处理间隔期内N点回波的多普勒频移向量,记为Fd:
Fd=[fd0,fd1,fd2,…,fdn,…,fdN-1],
(0≤n≤N-1 )
首点回波的多普勒频移fd0可由该点回波与前一组末点回波运算得到。以fd0为基准,将N点回波间的多普勒频移变化向量记为ΔFd,则有
ΔFd=[0,Δfd1,Δfd2,…,Δfdn,…,ΔfdN-1],
(0≤n≤N-1)
上式中,Δfdn=fdn-fd0。构造补偿因子向量K:K=[1,exp(-j2πΔfd1T),…,exp(-j2πΔfdnnT),…,exp(-j2πΔfdN-1(N-1)T)],(0≤n≤N-1)
进行如下运算,即可将多普勒频移变化补偿掉,使N点回波功率谱均处于一个多普勒通道之内:
Y(n)=S(n)·K(n)(0≤n≤N-1)
(13)
由此完成高速机动目标回波的运动补偿,具体补偿流程如图1所示。

图1 高速机动目标回波运动补偿流程图Fig.1 The flow chart of motion compensation to high speed maneuvering target echoes
2.2仿真验证
以一部发射单载频脉冲信号,具有高重频的L波段雷达对一高速运动目标进行探测作为仿真示例,这里仅考虑目标的径向速度,仿真参数设定见表3所示。采用MATLAB进行仿真分析。
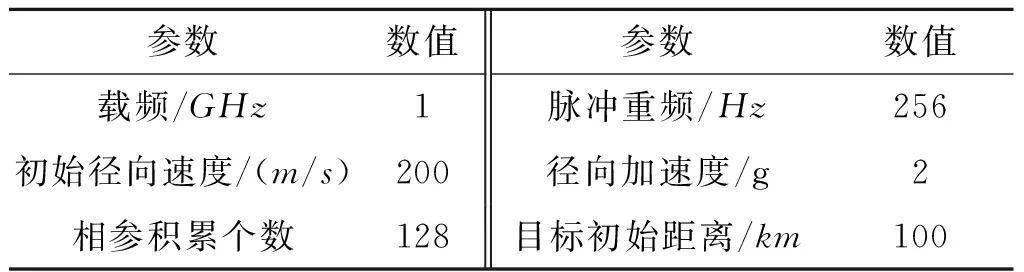
表3 仿真参数设定
仿真结果如图2和图3所示(仿真过程中应特别注意处理好三角函数的多值性)。图2 为原始回波及其频谱,图3 为补偿后的回波及其频谱。从图中可以看出:未补偿前,目标回波信号的频谱分布在多个通道内(类似线性调频信号谱),经补偿后,目标回波信号频谱集中到了一个通道内。
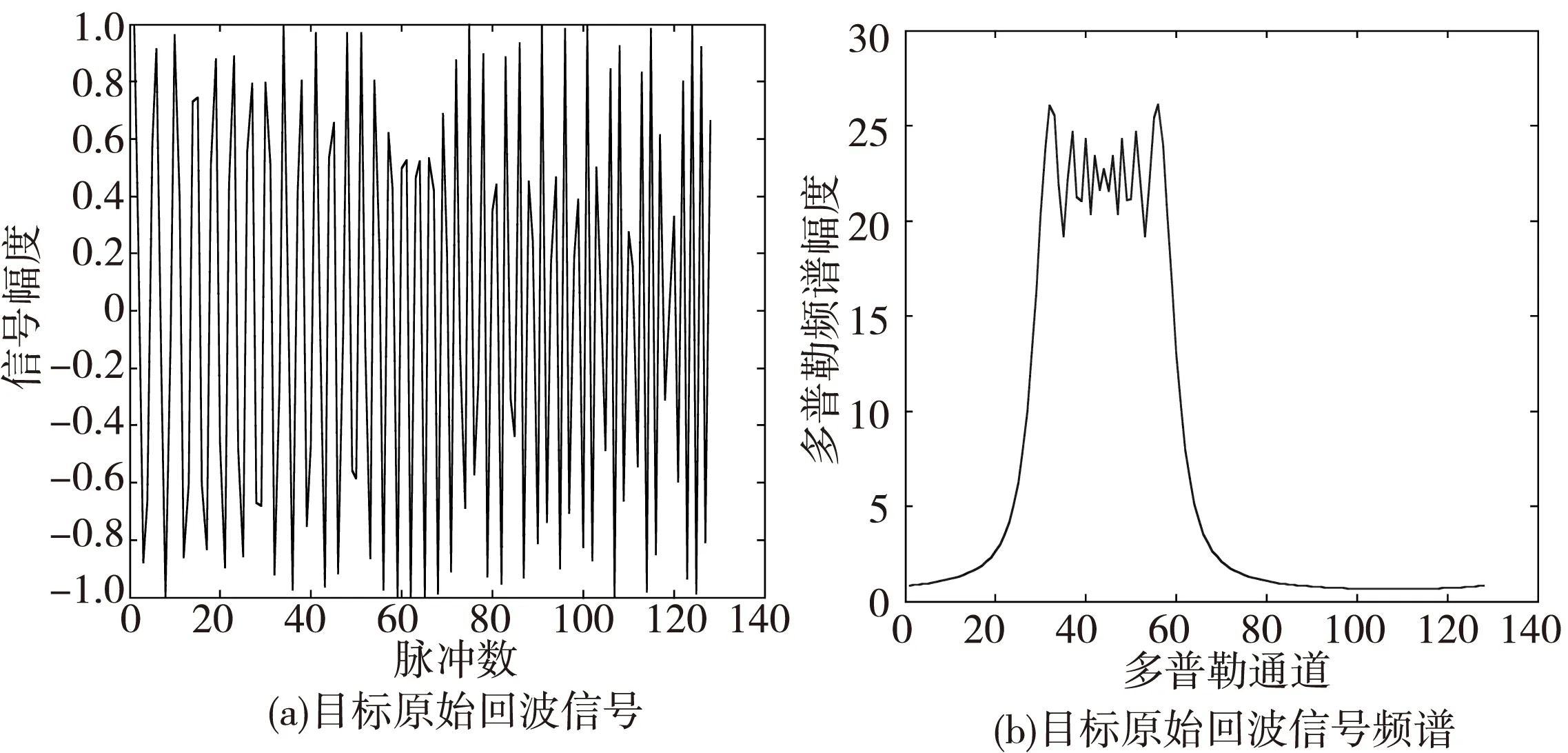
图2 目标原始回波信号与多普勒频谱Fig.2.target original echo signal and its Doppler frequency spectrum
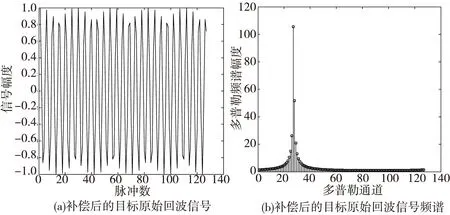
图3 补偿后的目标回波信号与多普勒频谱Fig.3 target echo signal after compensation and its Doppler frequency spectrum
3相参积累性能的仿真
假设在相参处理间隔期内高速机动目标回波的多普勒频移均匀变化,即Δfdn=nδfd0,则
fdn=(1+nδ)fd0(0≤n≤N-1)
(14)
式(14)中,fd0是回波起始时刻的基准多普勒频率,δ为多普勒频移变化率。高速机动目标回波序列模型为:
s(n)=Aexp[j(2πfdnTn+φ)]=
(15)
式(15)中,β=fd0/(fr/N),该量表示初始多普勒频率fd0所在的MTD通道序号。通过DFT滤波后第k通道的输出为:
(16)
功率为:
(n2-m2)δβ]}
(17)
式(17)求和结果的虚部为零,实部为含有菲涅耳(Fresnel)积分离散形式的复杂表达式。限于篇幅此处省略。
补偿后高速机动目标回波序列模型为:
sb(n)=Aexp[j(2πfdnTn+φ)]·
(18)
通过DFT滤波后第k通道的输出为:
(19)
功率为:
(0≤k≤N-1)
(20)
(21)
δ(·)为Dirac函数。当β=fd0/(fr/N)不为整数时,sinc函数主瓣采样值将小于其峰值,副瓣采样值虽较小,但并不为零,限于篇幅。本文暂不讨论这种情况。这里,选择一种特殊情形来定量的研究多普勒频移补偿的性能:设相邻回波数据间的多普勒频移是MTD通道宽度的整数倍L,且设初始多普勒 fd0正好为MTD通道宽度的P倍。仿真分析表明:只要回波数据足够多,从某个时刻起,其瞬时多普勒频率总会大于发射脉冲重复频率fr/2,原始回波频谱将产生折叠效应,造成原始回波频谱覆盖MTD的多个通道。根据我们选择的特殊情形以及前面的仿真分析,经多普勒补偿后的功率谱将聚集于MTD的第P号通道,且能量为信号总能量A2N2,为此,我们将补偿前、补偿后第P号通道的功率谱输出比定义为相参积累散焦损失ρ,即:
(n2-m2)δβ]}
(22)
以dB形式表示则为:
(23)
显然,相参积累散焦损失ρ与多普勒频移变化率δ、回波数据个数N、fr等多个因素有关,具体情况比较复杂。因此,下面以16点无加权MTD为例,针对多普勒频移为多普勒分辨单元的整数倍情况进行分析(非整数倍情况较为复杂, 留待以后研究):
1) 多普勒频移变化率为零时(δ=0),补偿前后回波的功率谱无变化,均处于一个多普勒通道之内,此时不存在散焦损失,或者说,散焦损失为零;
2) 多普勒频移变化率等于多普勒分辨单元N倍时(δ=1),实际上,由于折叠效应,原始回波的功率谱也始终处于同一个多普勒通道之内,相参积累损失ρ亦为零;
3) 当多普勒频移变化率为多普勒分辨单元的奇数倍时,若N为偶数,由于折叠效应,N点原始回波的功率谱将均匀且等幅的分布于N个多普勒通道中,每个多普勒通道仅占信号总能量的1/N,即A2N2/N=A2N,第P通道亦然,而补偿后第P通道的能量为信号总能量A2N2。则相参积累散焦损失为(ρ=20lg(A2N/A2N2)=-20logN),此为散焦损失最大之情形。
4) 当多普勒频移变化率为多普勒分辨单元的偶数倍时,只要N为偶数,原始回波的多普勒功率谱覆盖的通道数随倍数不同而各异,故其散焦损失也随倍数而异。
以上分析结果还可参见图4与表4所示。
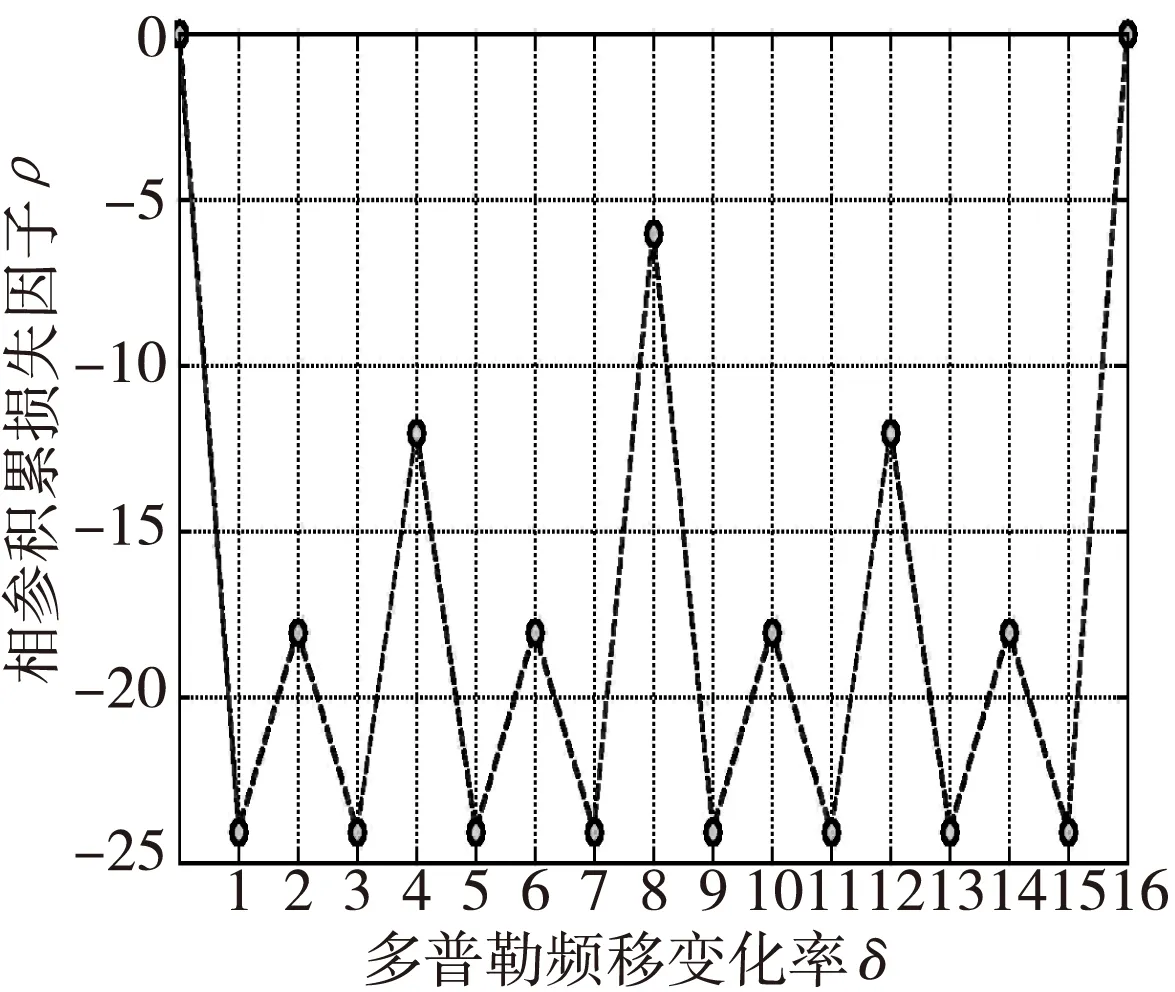
图4 多普勒频移变化率与相参积累散焦损失因子的关系Fig.4 Relationship of doppler frequency shift rate and coherent integration defocused loss factor
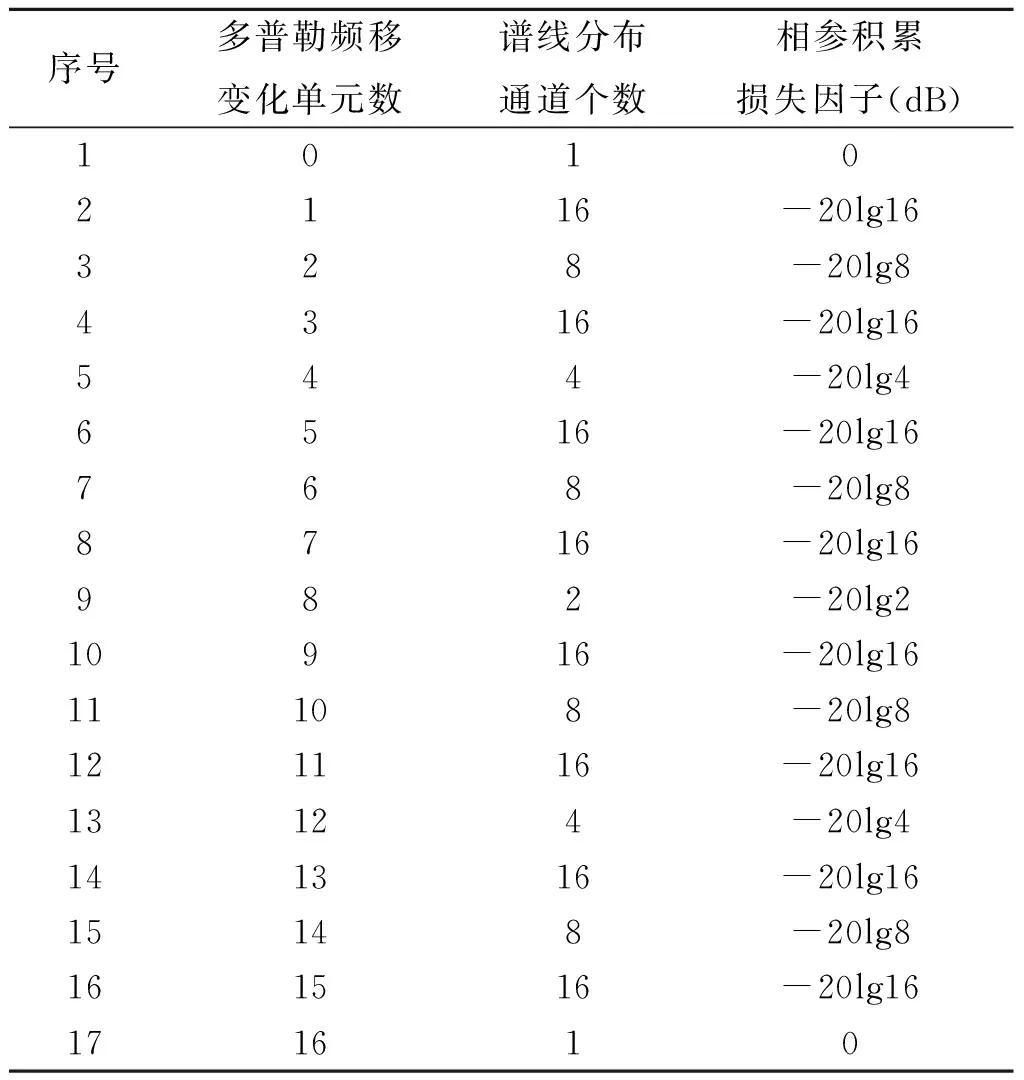
序号多普勒频移变化单元数谱线分布通道个数相参积累损失因子(dB)10102116-20lg16328-20lg84316-20lg16544-20lg46516-20lg16768-20lg88716-20lg16982-20lg210916-20lg1611108-20lg8121116-20lg1613124-20lg4141316-20lg1615148-20lg8161516-20lg16171610
4结论
本文提出了高速机动目标信号多普勒频移补偿方法,该方法可使相参处理间隔期内的N点回波的多普勒频率均处于一个多普勒通道之内,有效消除多普勒频移变化的影响,从而提高雷达对高速机动目标的检测能力。理论分析和仿真表明,该方法由于所需回波数量少,积累时间短,不必考虑距离徙动
等因素,故具有处理简单、计算量小、易于工程实现等优点。其不足之处是研究对象仅限于恒加速度运动目标,对于具有更高阶加速度的高机动目标补偿,寻找易于工程实现的补偿方法尚需后续研究。
参考文献:
[1]马晓岩,向家彬.雷达信号处理[M].长沙:湖南科学技术出版社, 1999.
[2]王军,林强,译.雷达手册[M].北京:电子工业出版社, 2003.
[3]王冬梅,李海,吴仁彪.一种机载变速动目标检测方法研究[J].现代雷达, 2012,34(2):33-36.
[4]苏军海,邢孟道,保铮.宽带机动目标检测[J].电子与信息学报, 2009, 31(6):1283-1287.
[5]苏洪涛,刘宏伟,保铮,等.天波超视距雷达机动目标检测方法[J].系统工程与电子技术,2004, 26(3):283-287.
[6]金添,黄晓涛,常文革.目标高速运动对一维像的影响及其校正方法[J].系统工程与电子技术, 2004,6(8):1019-1022.
[7]刘爱芳,朱晓华,刘中.基于修正离散Chirp Fourier变换的高速目标ISAR距离像补偿[J].航空学报, 2004,25(5):495-498.
[8]Feng Tongan, He Jin, Luo Ying. ISR Imaging of High Speed Moving Targets Based on Radon Transform[C]//Fifth International Conference on Information Assurance and Security.USA:IEEE,2009: 597-600.
[9]M Xing G, Wang Z Bao. High speed multi-target detection with narrow bandradar[J].IET Radar Sonar Navig. 2010, 4(4): 595-603.
[10]吴兆平,符渭波,苏涛,等.基于快速Radon-Fourier变换的雷达高速目标检测[J].航空学报, 2004,25(5):495-498.
[11]田建明,景建斌,韩广岐. 高超声速飞行器地面试验方法综述[J].探测与控制学报, 2013,35(5):57-60.
*收稿日期:2015-12-20
作者简介:董鹏曙 (1965—),男,湖北罗田人,教授,硕士研究生导师,研究方向:雷达装备发展与运用。E-mail:general_dps@163.com。
中图分类号:TN957
文献标志码:A
文章编号:1008-1194(2016)03-0066-05
DopplerFrequencyShiftandCoherentIntegrationPerformanceofHighSpeedManeuveringTargets
DONGPengshu,XIANGLong,XIEYoucai,JINJiagen
(AirForceRadarAcademy,Wuhan430019,China)
Abstract:Aiming at the coherent accumulation defocusing losses issue caused by Doppler frequency broadening of high speed maneuvering target, a target echo signal pre-processing method which could be easily realized in engineering was proposed. The influence of targets high speed and maneuvering to Doppler frequency was analyzed, and a relationship model of Doppler frequency shift associated with acceleration and turning rate was established. Theoretical analysis and simulation results demonstrated that the coherent integration defocused loss of MTD depended on Doppler frequency shift rate and other several factors, which was changed between -20 lgN dB and 0dB (N is the pulse number for coherent integration). With motion compensation, the influence of Doppler frequency shifted to the MTD coherent integration could be eliminated effectively; the detection ability of radar to high speed and maneuvering target in complex background could be enhanced.
Key words:high speed and maneuvering targets; motion compensation; detection; Doppler frequency shift rate
