基于节点状态加权平均的动力学网络同步
2016-07-22唐素芳肖玉柱
唐素芳,肖玉柱
(1.西安财经学院 统计学院,陕西 西安 710100;2.长安大学 数学与计算科学系,陕西 西安 710086)
基于节点状态加权平均的动力学网络同步
唐素芳1,肖玉柱2
(1.西安财经学院 统计学院,陕西 西安 710100;2.长安大学 数学与计算科学系,陕西 西安 710086)
摘要:为实现节点系统有参数失配的动力学网络的同步,以节点状态的加权平均为控制目标轨道设计实现网络同步的自适应控制方法,并利用微分方程的稳定性理论对该同步方法的有效性进行分析.结果表明,与现有的以节点系统的解为控制目标轨道的控制方法相比,该方法可用于结构未知的带有参数失配的动力学网络的同步,并且最终的同步轨道可以不是节点系统的解.通过数值模拟进一步证实了该方法的有效性.
关键词:自适应控制;参数失配;动力学网络
0引言
动力学网络是自然科学领域的重要研究课题.很多自然现象可由动力学网络的同步来解释,因而动力学网络同步得到各领域专家和学者的深入研究[1-2].实际中,网络受到各种不同的外界因素影响,各节点间很难自发地达到同步.为了实现网络各节点间的同步,学者们提出了一些控制方法. 文献[3]讨论了牵制控制方法. 选取部分节点加以控制就可实现整个网络的同步,因此牵制控制是一种很好的动力学网络同步的控制方法. 然而,在网络结构未知时控制节点的选定还是一个未解决的问题,并且该控制方法要求网络的各节点必须完全相同.
另一方面,网络同步的全节点控制方法也得到了一定的研究. 由于脉冲控制的结构简单,文献[4-5]讨论了结构未知的动力学同步的脉冲控制方法. 由于自适应控制的自动化、反应快速等优点,文献[6]讨论了动力学网络同步的自适应控制方法. 然而,这些控制方法都是以节点系统的一个解为控制目标轨道. 当节点系统的解无法获得不是稳定的同步流形时,这些控制方法或不能应用. 文献[7]以节点状态的平均为目标轨道,设计了网络的同步方法来解决上述问题,并且该方法也适用于有参数失配的动力学网络. 基于节点状态的加权平均,文献[8]设计了实现网络同步的脉冲控制方案. 本文以节点状态的加权平均为目标轨道,设计实现有参数失配的动力学网络同步的自适应控制方法,并通过理论分析该方法的有效性.
1自适应同步方案及理论分析
考虑由m个节点构成的动力学网络

(1)

(2)

在每个节点加上控制器ui=(u1,u2,…,un)T,则受控的网络为
(3)

(4)
定义同步误差
δxi=xi-x(t),i=1,2,…,m.
(5)
显然,同步误差服从方程

(6)
其中向量函数G(x)为

(7)
注意到同步误差满足
(8)
本文的目标是设计控制器ui(i=1,2,…,m)使系统(6)在原点稳定. 受文献[7-12]启发,引入如下自适应反馈控制器

(9)
(10)
(11)
其中γk和σkj是正常数.
由方程(11)得

(12)
为分析控制方法的有效性,给出如下假设.
假设1假设动力学网络(3)是有界的. 令Ω1⊂Rn和Ω2⊂Rmn是2个有界集, 并对x1,x2∈Ω1和y1,y2∈Ω2, 存在正常数l1,l2,使得
‖F(x1,pi)-F(x2,pi)‖≤l1‖x1-x2‖,
(13)
‖g(y1)-g(y2)‖≤l2‖y1-y2‖.
(14)
假设2∀x1=x2=…=xm=x∈Rn, 耦合函数gi(x1,x2,…,xm)满足
g1(x,x,…,x)=g2(x,x,…,x)=…=gm(x,x,…,x).
(15)
条件(13),(14)为一般性的李普希兹条件. 条件(15)为确保存在稳定的同步流形.在先前的研究中要求gi(x,x,…,x)=0或gi(x,x,…,x)+ui=0,因此同步目标轨道一定是节点系统的一个解. 由条件(15)知,本文的方法不需要同步目标轨道是节点系统的一个解.
为证明式(3),(9)~(11)构成的系统达到同步,引入如下非负函数

其中L为可选择的常数.对V求微分,并利用式(8)得
(16)
式(16)中
(17)
及
(18)
将式(17)~(18)带入式(16)得
利用假设1和假设2,得


2数值算例
为表述方便,引入如下标量

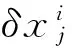


统一混沌系统可描述为
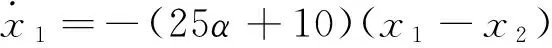

3结束语
基于网络节点状态的加权平均,设计了实现有参数失配的动力学网络同步的自适应控制方法,并基于微分方程的稳定性理论分析了方法的有效性. 与先前以节点系统的解为控制目标轨道的控制方法相比,该方法适用于有参数失配的动力学网络,且同步目标轨道不必是节点系统的解. 与先前以节点状态的平均值为同步目标轨道的同步方法相比,该控制方法的控制系统结构更加简单,且控制过程中信息的传递量更小.文中网络的每个节点是由一般的常微分方程描述,实际中节点可由其他类型方程来描述,如分数阶系统. 将此方法推广到这类网络系统还有待进一步研究.
参考文献(References):
[1]OSIPOVGV,KURTHSJ,ZHOUC.Synchronizationinoscillatorynetworks[M].Berlin:Springer,2007.
[2]武相军.复杂混沌动力学网络系统的同步及其应用研究[D].上海:上海交通大学,2011.
WUXiangjun.Synchronizationofchaoticcomplexdynamicalnetworkanditsapplication[D].Shanghai:ShanghaiJiaotongUniversity,2011.
[3]LIXiang,WANGXiaofang,CHENGGuanrong.Pinningacomplexdynamicalnetworktoitsequilibrium[J].IEEETransCircuitsSystI,2004,51(10):2074-2087.
[4]LIUBin,LIUXinzhi,CHENGuanrong,etal.Robustimpulsivesynchronizationofuncertaindynamicalnetworks[J].IEEETransCircuitsSystI,2005,52(7):1431-1441.
[5]LUJianquan,HODWC,CAOJinde,etal.Singleimpulsivecontrollerforgloballyexponentialsynchronizationofdynamicalnetworks[J].NonlinearAnal:RealWorldAppl,2013,14(1):581-593.
[6]ZHOUJin,LUJunan,LYUJinhu.Adaptivesynchronizationofanuncertaincomplexdynamicalnetwork[J].IEEETransAutomatControl,2006,51(4):652-656.
[7]XIAOYuzhu,XUWei,LIXiuchun,etal.Adaptivecompletesynchronizationofchaoticdynamicalnetworkwithunknownandmismatchedparameters[J].Chaos,2007,17(3):109-113.
[8]ZHANGGang,LIUZenggrong,MAZhongjun.Synchronizationofcomplexdynamicalnetworksviaimpulsivecontrol[J].Chaos,2007,17(4):751-763.
[9]LUWenlian,CHENTianping.Newapproachtosynchronizationanalysisoflinearlycoupledordinarydifferentialsystems[J].PhysicaD,2006,213(2):214-230.
[10]HUANGDebin.Simpleadaptivefeedbackcontrollerforidenticalchaossynchronization[J].PhysRevE,2005,71(3):142-154.
[11]肖玉柱,唐素芳.基于节点状态输出的动力学网络的自适应同步[J].动力学与控制学报,2014(2):127-131.
XIAOYuzhu,TANGSufang.Adaptivesynchronizationofdynamicalnetworkusingstatesofnodesastargetorbitc[J].JournalofDynamicsandControl,2014(2):127-131.
[12]刘洪涛,郭永峰.两拓扑不等价混沌系统的同步控制[J].纺织高校基础科学学报,2010,23(2):233-236.
LIUHongtao,GUOYongfeng.Synchronizationcontroloftwotopologicallyineqivalentchaoticsystem[J].BasicSciencesJournalofTextileUniversities,2010,23(2):233-236.
[13]LYUJinhui,CHENGuangrong,CHENGDaizhan,etal.BridgethegapbetweentheLorenzsystemandChensystem[J].IntJBifurChaos,2002,12(2):2917-2926.
[14]杨丽新,刘晓君.分数阶混沌系统的投影同步[J].纺织高校基础科学学报,2012,25(1):75-78.
YANGLixin,LIUXiaojun.Projectivesynchronizationofanewfractional-orderchaoticsystem[J].BasicSciencesJournalofTextileUniversities,2012,25(1):75-78.
编辑、校对:师琅
文章编号:1006-8341(2016)02-0204-06
DOI:10.13338/j.issn.1006-8341.2016.02.012
收稿日期:2015-07-18
基金项目:国家自然科学基金资助项目(11202035); 陕西省教育厅科研计划资助项目(14JK1276)
通讯作者:唐素芳(1980—),女,辽宁省辽阳市人,西安财经学院讲师,博士,研究方向为偏微分方程.
中图分类号:O 415.5
文献标识码:A
Synchronization of dynamical network via weighted average of several nodes′ states
TANGSufang1,XIAOYuzhu2
(1.School of Statistics, Xi′an University of Finance and Economics, Xi′an 710100,China;2.Department of Mathematics and Information Science, Chang′an University, Xi′an 710086,China)
Abstract:An adaptive control method was designed to synchronize the dynamical network with unknown parameter mismatch and coupling structure. In this method, the weighted average of several nodes′ states was used as target orbit. Based on the invariance principle of differential equation, the conditions of asymptotic synchronization were obtained. Compared with previous synchronization methods via a solution of node system used as target orbit, this method is applicable to networks with parameter mismatch, and the synchronization manifold can not be a solution of uncoupled system. Meanwhile, one numerical example is performed to demonstrate the effectiveness of the proposed method.
Key words:adaptive control; parameter mismatch; dynamical network
E-mail:sufangtang@163.com
引文格式:唐素芳,肖玉柱.基于节点状态加权平均的动力学网络同步[J].纺织高校基础科学学报,2016,29(2):204-209.
TANG Sufang,XIAO Yuzhu.Synchronization of dynamical network via weighted average of several nodes′ states[J].Basic Sciences Journal of Textile Universities,2016,29(2):204-209.
