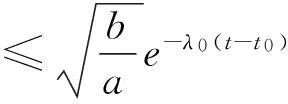执行器部分失效的时滞系统稳定性分析

刘慧巍

(渤海大学 工学院，辽宁 锦州 121013)



执行器部分失效的时滞系统稳定性分析

刘慧巍

(渤海大学 工学院，辽宁 锦州 121013)

摘要：针对时滞系统给出了一种控制器设计方法，使系统在执行器发生部分失效时，仍然能使系统状态指数稳定.针对执行器部分失效和正常执行两种情况，本文把时滞系统转化为切换系统，应用平均驻留时间及多Lyapunov函数方法，给出系统状态指数稳定的线性矩阵不等式形式条件.

关键词：时滞系统;平均驻留时间;切换系统;多Lyapunov函数

0引言

在大多数实际工程应用中,控制系统运行的可靠性是最关键的因素，往往受到最多关注，如果控制系统中的元器件(如执行器)出现故障,可能会使受控对象性能变差甚至运行不稳定、执行器失效〔1〕.近年来，针对执行器失效的研究逐渐成为热点〔2-5〕，学者及研究机构对其重视程度越来越高，尤其在卫星姿态控制〔6〕、水下机器人〔7〕等远距离、不可视、受控对象运行环境恶劣等条件下，执行器失效问题尤为突出.针对一类网络化控制系统可能存在的执行器失效，文献〔4〕利用Lyapunov-Krasovskii泛函方法，给出了控制器设计并给出了矩阵不等式条件形式的系统渐进稳定判定定理.对于时变执行器和传感器发生故障时，文献〔8〕将一类线性系统将问题转化为增益优化问题，文中设计的控制策略使时变执行器和传感器故障失效给系统造成的影响大幅降低.文献〔9〕针对一类不确定随机切换非线性系统，研究了系统的鲁棒可靠性控制问题，在执行器失效情况下，应用驻留时间方法，给出能可靠控制的控制器设计，保证了系统在随机切换时几乎必然指数稳定.本文运用平均驻留时间方法，研究了一类线性时滞系统在执行器失效情况下的系统稳定性问题.

1问题描述及预备知识

考虑如下线性系统

(1)

其中x(t)∈Rn为系统状态向量，A,E,B为具有适当维数的已知常数矩阵，h为系统时滞常数，u(t)为系统输入向量，φ(θ)为已知连续函数.

我们将系统执行器正常执行和执行器部分失效两种情况系统模型分别表示为如下形式:

(2)

由(2)式，将系统(1)转化为如下切换系统形式：

(3)

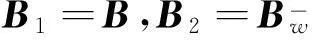
uσ(t)(t)=Kσ(t)(t)x(t)

(4)

Kσ(t)为控制器增益.

定义1平衡点x*=0称为系统(1)在切换信号σ(t)下是指数稳定的，如果对初始条件t0∈0∪R+,φ(t)∈Cn，存在常数Γ>0，γ>0，使得系统(1)的解x(t,t0,φ(t))满足

‖x(t0,t,φ(t)‖≤Γ‖x(t0)‖e-γ(t-t0)

2主要结果

考虑系统(3)中σ(t)=1时的情况，备选Lyapunov函数选择如下形式：

(5)

引理1对于任意给定的常数h>0和λ0，如果存在正定矩阵P1,Q1,使下面线性矩阵不等式成立：

(6)

则有V(x(t))

证明此时将系统(3)控制器选为u(t)=K1x(t)，K1=-BTP，则沿系统(3)的轨迹，V(x(t))对时间的求导，可得

=xT(t)(ATP1+P1A+Q1-2P1BBTP1)x(t)+xT(t-h)ETP1x(t)+xT(t)P1Ex(t-h)-

xT(t-h)ETP1x(t)+xT(t)P1Ex(t-h)-e-2λ0hxT(t-h)Q1x(t-h)

下面考虑系统(3)中σ(t)=2时的情况，备选Lyapunov函数如下式所示：

(7)

引理2对于任意给定的常数h>0和λ0>0，如果存在正定矩阵P2，Q2,使得下面的线性矩阵不等式成立：

(8)

xT(t-h)ETP2x(t)+xT(t)P2Ex(t-h)-e-2λ0hxT(t-h)Q2x(t-h)

现考虑时滞切换系统(3)，基于已得结果引理1及引理2，下面给出本文的主要结果.

定理1对于任意给定的常数h>0和λ0>0，如果存在正定矩阵Pi,Qi(i=1,2)，使得(6)式和(8)式成立，且满足条件(S1)和(S2)，则系统(3)是指数稳定的，且状态估计满足

(9)

其中

(10)

λ(P)表示矩阵P 的特征值.μ>1且满足：

Pi≤μPj,Qi≤μQj,∀i,j∈M

(11)

条件(S2) :令Nσ(t0,t)表示(t0,t)内切换次数，平均驻留时间τα满足下面不等式

证明：对系统(3)，备选分段Lyapunov函数形式如下：

(12)

Pi,Qi(i=1,2)分别满足(6)式和(8)式.由Lyapunov函数(12)及(11)式可知

Vi(x(t))≤μVj(x(t)),∀i,j∈M

(13)

对任意给定t>0，令ti(i=1,2,…k)表示在(t0,t)内的切换时刻，且t0

(14)

由(13)可得

V(x(t))≤Vσ(tk)(x(tk))e2λ0T+(tk,t)-2λ0T-(tk，t)≤μVσ(tk)(x(tk))e2λ0T+(tk,t)-2λ0T-(tk,t)

≤μVσ(tk-1)(x(tk-1))e2λ0T+(tk-1,t)-2λ0T-(tk-1,t)≤…

≤μNσ(t0，t)Vσ(t0)(x(t0))e2λ0T+(t0,t)-2λ0T-(t0,t)

=e2λ0T+(t0,t)-2λ0T-(t0,t)+Nσ(t0，t)lnμVσ(t0)(x(t0))

再由条件(S1)、(S2)，则可得到如下不等式

(15)

由(10)式及(12)式可知不等式a‖x(t)‖2≤Vx(t)≤b‖x(t)‖2成立，进而联合(15)式即可得

(16)

参考文献：

〔1〕谢立.执行器失效不确定时滞系统的指定衰减度鲁棒可靠控制〔J〕.传感技术学报:2005,18(3) :460-465.

〔2〕WANG W,WEN C.Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance〔J〕.Automatica,2010,46(12): 2082-2091.

〔3〕TIAN E,YUE D,YANG T C,et al.T-S fuzzy model-based robust stabilization for networked control systems with probabilistic sensor and actuator failure〔J〕.IEEE Transactions on Fuzzy Systems,2011,19(3): 553-561.

〔4〕PENG C,YANG T C,TIAN E G.Robust fault-tolerant control of networked control systems with stochastic actuator failure〔J〕.IET Control Theory & Applications,2010,4(12): 3003-3011.

〔5〕TONG S,WANG T,LI Y.Fuzzy adaptive actuator failure compensation control of uncertain stochastic nonlinear systems with unmodeled dynamics〔J〕.IEEE Transactions on Fuzzy Systems,2014,22(3): 563-574.

〔6〕MA Y,JIANG B,TAO G,et al.Actuator failure compensation and attitude control for rigid satellite by adaptive control using quaternion feedback〔J〕.Journal of the Franklin Institute,2014,351(1): 296-314.

〔7〕CORRADINI M L,MONTNTERIU A,ORLANDO G.An actuator failure tolerant control scheme for an underwater remotely operated vehicle〔J〕.IEEE Transactions on Control Systems Technology,2011,19(5): 1036-1046.

〔8〕CAI X J,WU E.Robust parameter-dependent fault-tolerant control for actuator and sensor faults〔J〕.International Journal of Control,2010,83(7):1475-1484.

〔9〕XIANG Z R,WANG R H,CHEN Q W.Robust reliable stabilization of stochastic switched nonlinear systems under asynchronous switching〔J〕.Applied Mathematics and Computation,2011,217(19):7725-7736.

Stability analysis of time-delay systems with actuator partial failure

LIU Hui-wei

(College of Engineering,Bohai University,Jinzhou 121013,China)

Abstract：A controller design method is provided in this paper for time-delay system that ensure the state of system be exponentially stable when the actor partial failure happens.The time-delay system is transformed to a switching system in this paper for the scenes of actor running formally and actor partial failure.With application of average dwell time and multiple Lyapunov functional mothed,a sufficient condition is given in form of linear matrix inequality for exponential stability of the switching system states.

Key words：time-delay system; average dwell time; switching system; multiple Lyapunov functions

收稿日期：2015-04-15.

基金项目：国家自然科学基金项目(No: 11544013)；国家自然科学基金项目(No: 11404032)；国家自然科学基金项目(No: 11305016).

作者简介：刘慧巍(1979-),男,讲师,从事网络化控制系统理论方面研究.

通讯作者：liuhuiwei0158@163.com.

中图分类号：TP13

文献标志码：A

文章编号：1673-0569(2016)02-0155-05