关于人体血液自然分布收纳单位同型系统间联系的几个问题
2016-07-22蒋术一蒋宏岩
李 琦,蒋术一,蒋宏岩
(1.渤海大学 数理学院,辽宁 锦州 121013; 2.中国医科大学附属盛京医院妇产科,辽宁 沈阳 110001;3.锦州市中心血站,辽宁 锦州 121000)
关于人体血液自然分布收纳单位同型系统间联系的几个问题
李琦1,蒋术一2,蒋宏岩*,3
(1.渤海大学 数理学院,辽宁 锦州 121013; 2.中国医科大学附属盛京医院妇产科,辽宁 沈阳 110001;3.锦州市中心血站,辽宁 锦州 121000)
摘要:随着人体是由血液自然分布收纳单位构成这一概念的提出,也给出了血液自然分布收纳单位同型系统的同态、同构概念,并引入了血液自然分布收纳单位给定系统的诱导系统,利用对应及同态公式,刻划了活体中血液自然分布收纳单位同型与同态的密切关系,并对血液自然分布收纳单位的同态(同构)不变性问题进行了讨论,得出了一些相关应用结果.
关键词:血液自然分布收纳单位;同型系统;同态对应;同构对应
0引言
以肺为中心、为参照系的血液自然上行下行运动是人体内存在的血液运动公理,人体可看成是由血液自然分布收纳单位构成.血液自然分布收纳单位具有同态、同构的性质〔1-4〕.血液自然分布收纳单位具有同型性〔5-8〕.对同型系统的血液自然分布收纳单位的同构与同态对应的相关理论进行的研究是有益的.
1人体血液自然分布收纳单位同型系统的概念
依血液的分布与收纳这一特征来观察,可以发现人体是由血液自然分布收纳单位构成.无论是肺脏、肝脏、心脏、骨骼、肌肉、胃肠等均可视为一个分别由动脉血液的分布与对应的静脉血液收纳构成的各个系统,其中每一个系统又均具有同型性.
定义1无论是人体的整体,还是任一器官做为一个血液自然分布收纳单位系统均可用一个对子A=(A;R)来表达,其中A是非空集合,称为人体血液自然分布收纳单位系统的基础集,而R是A上有限元关系集合.R可良序化为
R={r1,r2…,rn}
其中ri为mi元关系,称
M={m1,m2,…,mn}
为血液自然分布收纳单位系统A的型,也可记为MA或M(R).
定义2两个血液自然分布收纳单位系统A=(A;RA)和B=(B;RB),如果两个血液自然分布收纳单位具有相同的型,即MA=MB,那么A和B称为同型的血液自然分布收纳单位系统,这时RA和RB可不加区分,都记为R.
系统的区别:人体系统的区别不仅表现在是否体系一致,更重要的区别是反映在关系集合R的区别.
例1左肺A=(左肺动脉血液分布与左肺静脉血液收纳对应与右肺B=(右肺动脉血液分布右肺静脉血液收纳对应),左肺与右肺两个系统的主要功能均为气体交换,这两个系统的关系集R相等时,两个系统可以肯定是同型系统.
例2同型系统只是型相同,关系集R不一定相等,可认作是不同的系统.A=(肝脏分泌胆汁)与B=(肾脏动脉血过滤产生尿液)是2个系统,肝脏与肾脏均由动脉血液的分布与静脉血液的收纳分别产生胆汁和尿液,由同型系统的定义可知,A和B是同型系统,但只是型相同,关系集R并不相等.
2人体同型系统之间的同态对应与同构对应
人体内存在以肺为中心的血液自然上行下行运动这一公理,来自于肺脏的动脉血液下行分布至全身不同的组织结构,虽然动脉血液在下行运动中分布于组织结构不同的各个血液自然分布单位,但其动脉分布血液的来源和运动状态相同,即下行动脉血液的分布为同态分布,但却不同构.
上行静脉血液收纳上行,出右心后分布于组织结构相同的肺脏,且分布的静脉血液状态相同,即上行静脉血液为同态、同构分布.在以肺脏为中心(为参照系)的血液自然上行下行运动这一公理中,在以实验为证据观察中我们可以得出以下结论:
(1)在以肺为中心的血液自然上行下行运动过程中,上行血液与下行血液为同态分布对应.在同一组织、脏器内上行下行血液为既同态又同构对应.如脾动脉与脾静脉为既同态对应又同构对应.
(2) 人体中来自肺脏的下行动脉血液出左心后是以同态不同构的方式分布于全身.
(3)上行静脉血液出右心后是以同态又同构的方式分布于肺脏.
(4)下行动脉血液是以同态又同构的方式分布于具体的肝、脾、肾、心、胃、肠、骨骼、肌肉等组织结构.
(5)人体同型系统之间的同态对应与同构对应的特征可对人体的整体和部分做出层次划分.从人体整体上观察,上行下行血液是同态对应;具体到组织器官,即第二个层次的上行下行血液运动表现的形式为既同态对应又同构对应.
(6)人体内存在双态分布,单态对应.肝脏的血液分布为双态同构分布,肝脏既接受肝动脉的血液分布又接受来自于胃肠道的肝门静脉的血液分布.肝静脉与这一双态分布相对应.
定义3设A=(A;R)和B=(B;R)是人体两个同型系统,φ:A→B是从集合A到集合B的对应,
(1)若对于任意的r∈R,r为n元的,且对任意的a1,a2,…an∈A,当(a1,a2,…an)∈r时,有(φ(a1),φ(a2)…,φ(an))∈r,则φ称为从A到B的血液自然分布收纳单位同态对应,且称A和B的血液自然分布收纳单位是同态的.一切从血液自然分布收纳单位系统A到R的同态对应组成的集合记为hom(A,B).
(2)如果φ:A→B是从血液自然分布收纳单位A到B的同态对应,φ是一个满对应,即满足于对于任意的r∈R,r为n元运算,b1,b2,…,bn∈B,(b1,b2,…,bn)∈r,必存在a1,a2,…an∈A使得(a1,a2,…an)∈r,且有bi=φ(ai),i=1,2,…,n,则称B是A的同态象,称φ是从A到B的满同态.
(3)若φ是从A到B的满同态对应,且φ是单射的,则称φ是从A到B的同构对应,称A和B是同构的.一切从血液自然分布收纳单位A到B的同构对应作成的集合记为Isom(A,B).
(4)特别是,当A=B时得到血液自然分布收纳单位自同态对应与自同构对应,并分别记作hom(A)和Isom(A).
例2设A=(A;R)是任意系统.则IA:A→A是A上的自同构对应.
由以上定义易得下列性质:
性质设A=(A;R),B=(B;R),C=(C;R)是三个系统,∘为复合运算
(1)若φ∈hom(A,B),ψ∈hom(B,C),则ψ∘ φ∈hom(A,C);
(2)若φ∈Isom(A,B),ψ∈Isom(B,C),则ψ∘ φ∈Isom(A,C);
(3)恒等对应,IA:A→∈Isom(A);
(4)血液自然分布收纳单位自同构对应一定存在自同态对应,故有Isom(A)⊆hom(A).
3给定的血液自然分布收纳单位存在诱导系统
人体通过诱导生成的系统也可看作是由原血液自然分布收纳单位系统生成的一个新系统.产生诱导系统的过程,可以看做是在人体生长发育过程中,原血液自然分布收纳单位消失与新血液自然分布收纳单位生成的基本运动形式.
定义4设A=(A;F)是人体任意系统,其中F={f1,f2,…,fk},F良序化的型为
M(F)={n1,n2,…nk}
对于F中的任意ni元关系fi(i=1,2,…,k),定义为
fi:afi∈A,ni=0;
其中a1,a2,…ani,ani+1,ni∈A,可由fi诱导A上的一个ni+1元关系:
r(fi)⊆A,r(fi)={afi},ni=0;
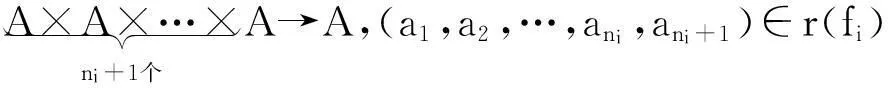
f(a1,a2,…ani)=ani+1,ni>0.
令R={r(f1),r(f2),…,r(fk),},则由系统的定义易知A=(A;R)是一个系统,称为由系统A=(A;F)诱导的系统,记为A(r(F))=(A;r(F)),其型为
M={m1,m2,…,mk},其中mi=ni+1,i=1,2,…,k.
例3一个肺脏系统S=(M;R),M是由所有功能血液自然分布收纳单位组成的集合,R是血液自然分布收纳单位间的关系,是血液自然分布收纳单位间的关系集,从胚胎到成人的发育其血液自然分布收纳单位不断升级,实质就是由原有的肺血液自然分布收纳单位系统诱导生成一个功能更完备的新系统.
关于人体同型系统的同态与其诱导系统的同态之间的关系有以下结论:
定理1若A(A;F)和B=(B;F)是两个同型系统,则
hom(A,B)=hom(A(r(F),B(r(F)))
特别的,有hom(A)=hom(A(r(F))).
证明设:φ:A→B是从A到B的任意同态对应,即φ∈hom(A,B),任取r(fi)∈r(F),a1,a2,…,ami∈A,且(a1,a2,…,ami)∈r(fi),因为
φ(ami)=φ(ani+1)=φ(fi(a1,a2,…,ani))=fi(φ(a1),φ(a2),…,φ(ani)),
所以
(φ(a1),φ(a2),…,φ(ani),φ(ani+1))∈r(fi),
即
(φ(a1),φ(a2),…,φ(ami))∈r(fi),
因此φ∈hom(A(r(F),B(r(F))).
反之设φ∈hom(A(r(F),B(r(F))),r(fi)∈r(F)是mi元关系,a1,a2,…,ami∈A,
则
(a1,a2,…,ami)∈r(fi)⟹(φ(a1),φ(a2),…,φ(ami))∈r(fi),
即
fi(a1,a2,…,ani)=ani+1=ami⟹fi(φ(a1),φ(a2),…,φ(ani))=φ(ani+1)=φ(ami),
因此有
φ(fi(a1,a2,…,ani))=φ(ami)=fi(φ(a1),φ(a2),…,φ(ani)),
所以φ∈hom(A,B).
进而,可以得到关于人体同型系统的同构与其诱导系统的同构之间的关系:
定理2若A=(A;F)和B=(B;F)是两个同型系统,则
Isom(A,B)=Isom(A(r(F),B(r(F)))
特别的,有Isom(A)=Isom(A(r(F))).
4人体血液自然分布收纳单位同型系统的同构不变性和同态不变性
定义5(1)设人体血液自然分布收纳单位系统A=(A;R)是任一具有性质P的系统,若血液自然分布收纳单位A的任一子系统同态象也具有性质P,即对于任意的血液自然分布收纳单位满同态对应φ:A→B,血液自然分布收纳单位系统B=(B;R)也具有性质P,则称P为血液自然分布收纳单位同态不变性.
(2)设人体血液自然分布收纳单位系统A是任一具有性质P的血液自然分布收纳单位系统,若血液自然分布收纳单位A的任一同构系统B也具有性质P,则称P为一个同构不变性.
由血液自然分布收纳单位同态(同构)不变性可知,当B是A的一个同态(或同构)血液自然分布收纳单位系统时,如果对血液自然分布收纳单位B的性质不了解,则可通过同态(同构)函数将血液自然分布收纳单位A的具有同态(同构)不变性的性质带到血液自然分布收纳单位B中去.因此,在研究一个新的人体血液自然分布收纳单位系统时,可先考虑它是否与已有的血液自然分布收纳单位系统同态或同构,以便做进一步的比较分析.
参考文献:
〔1〕钱学森.论系统工程〔M〕.长沙:湖南科学技术出版社,1982.
〔2〕蒋宏岩,蒋术一.肺与血液的自然运动〔M〕.长春:吉林大学出版社,2012.
〔3〕胡庆平,李丹.系统间的一类联系——同态与同构〔J〕.昭通师范高等专科学校学报,2002(5):5-11.
〔4〕蒋术一,蒋宏岩.整合医学理论与公理化体系的建立〔J〕.医学争鸣,2014,5(1): 22-24.
〔5〕王彩霞,张娟娟.关于同型系统间的联系的几个问题〔J〕.西安文理学院学报:自然科学版,2010,13(1): 15-17.
〔6〕刘绍学.近世代数基础〔M〕.北京:高等教育出版社,1999.
〔7〕陈建明,曾明.离散的数学结构〔M〕.北京:高等教育出版社,2006.
〔8〕蒋术一,蒋宏岩.血液自然运动与中西医理论的整合统一〔J〕.医学争鸣,2014,5(3): 19-22.
Homomorphic mapping and isomorphic mapping between homotypic systems of human blood natural distribution- acceptation unit
LI Qi1,JIANG Shu-yi2,JIANG Hong-yan3
(1.College of Mathematics and Physics,Bohai University,Jinzhou 121013,China; 2.Department of Obstetrics Gynecology Shengjing Hospital China Medical University 110001; 3.Jinzhou Centre Blood Station 121000,China)
Abstract:On the basis of blood natural distribution- acceptation unit,The concept of homomorphism and isomorphism of homotypic system is proposed,Using the mapping and homotypic formula,we illustrated the close relationship between homomorphism (isomorphism) of blood natural distribution-acceptation unit.It was debated on the question of invariance property of blood natural distribution-acceptation and get some relevant application results.
Key words:blood natural distribution- acceptation unit;homotypic system;homomorphic mapping;isomorphic mapping
收稿日期:2015-02-10.
基金项目:辽宁省教育厅项目(No:L2014443).
作者简介:李琦(1963-),女,副教授,主要从事人体一般系统结构理论方面的研究.
通讯作者:jsyjhy2013@126.com.
中图分类号:O153
文献标志码:A
文章编号:1673-0569(2016)02-0105-04
