非牛顿流体石油管流动研究进展及建议

李孝军，刘永刚，林　凯，刘文红

(中国石油集团石油管工程技术研究院，石油管材及装备材料服役行为与结构安全国家重点实验室　陕西　西安　710077)



·综述·

非牛顿流体石油管流动研究进展及建议

李孝军，刘永刚，林凯，刘文红

(中国石油集团石油管工程技术研究院，石油管材及装备材料服役行为与结构安全国家重点实验室陕西西安710077)

摘要：从研究非牛顿流体流动数学模型及其求解方法、原油圆管分层流与非定常流、环空管流流动规律、非牛顿流体流动流态判别及非牛顿流体流动实验等5个方面，综述了21世纪始10余年国内外非牛顿流体石油管流动现状。非牛顿流体流动本构方程的建立和流变参数的确定，是研究非牛顿流体流动和流变特性的基础，对发展非牛顿流体力学理论和解决生产技术问题都至关重要。总结前人研究成果的基础上，根据非牛顿流体石油管流动的发展状况，提出将高分子材料学、电磁场理论、弹塑性力学理论、混沌学、现代计算机有限元数值模拟等学科与高等流体力学相结合的方式，寻求非牛顿流体管流流动中分层流混输技术、非定常流动稳定性与流动规律、环空紊流流动规律和流态判据的相关性与合理性等亟待解决问题的思路。

关键词：非牛顿流体；数学模型；管流；环空流；流态；仿真试验

0引言

石油工业中的钻井液、水泥浆、含蜡原油和聚合物水溶剂等都是非牛顿流体，其各种流动现象的理论和实验研究一直受到人们的重视，但目前还未找到适用于所有非牛顿流体的本构方程[1-4]。现在的研究方法是把非牛顿流体分成若干类，如非时变性流体、粘弹性流体、触变性流体和震凝性流体等，通过理论和实验研究找到各自的本构方程，分别研究它们的流动现象，得出各种流动问题的解[5-8]。目前，非牛顿流体石油管流动研究处于世界领先地位的挪威，也只研究了在某些特殊情况下一些简单的流动现象，如管内流动的解析解[9-12]。然而，这些初步的进展为这些流体的其它流动现象研究提供了方法和理论基础[13-16]。非牛顿流体在水平井和稠油开采井中的环空流动，从层流到过渡流再到紊流的变化规律，受流体流变性、井眼与管柱内外径比和管柱偏心度的影响。采出到地面管线的较大流性指数非牛顿流体与低粘牛顿流体的混输，可实现节能降耗，提高管输效率。非牛顿非定常流处于混沌状态，可着眼于海洋管非牛顿水合物段塞流的研究。而且，随着现代计算机技术的飞速发展，精确的数值模拟对非牛顿流体流动研究也起着至关重要的作用，为本世纪非牛顿流体石油管流动机理研究带来了新的契机。

1非牛顿流体数学模型及其求解方法

长期以来，非牛顿流体数学模型的研究和求解是高校和科研院所的研究领域之一，能量耗散模型也是其研究热点。2002年，张劲军和严大凡[1]根据剪切率和能量耗散率定义，建立幂律流体湍流剪切率与能量耗散率的关系式，提出了一种幂律流体管内湍流能量耗散率的近似算法。2004年，殷谷良和董柏青[2]讨论一类带p幂增长耗散位势的非牛顿模型解的渐近性态，利用改进的Fourier分解方法证明了其解在L2范数下衰减率为(1+t)-n/4。2010年，张其亮和张兴伟等[3]利用Stokes算子的谱分解法和Lp-Lq估计研究一类三维不可压缩非牛顿流体弱解的最优代数衰减速率，证明了初速度在L2范数下其弱解的衰减率为t-5/4。由此，得到了非牛顿流体在剪切作用下流速随时间衰减的最优代数衰减率。

在非牛顿流体流动方程解的存在性证明基础上[4-7]，清华大学朱克勤和东北石油大学崔海清各自带领的科研团队在非牛顿流体石油管流动建模求解方面做了大量的深入研究。朱克勤等[8-10]提出了一种用弹簧和油壶连接的分形网络结构来比拟分数元模型的应力-应变特性，利用Heaviside运算微积，证明了该结构对应的粘弹性流体为1/2阶导数的分数元，还导出分数元模型的圆管起动流的解析解；研究了同心环空宾汉流体的C-P流，得到了不同流动类型的解析解，发现了2种新的流型，依据宾汉数、轴向库艾特数和半径比3个无量纲量，从数理视角划分出了8种不同的速度分布形式；推导了圆管内幂律流体分层Poiseuille流动的控制方程和基本流动解析解，进而得到该流动的小扰动线性控制方程，采用切比雪夫配点法引入虚拟网格求得了扰动方程的数值解，解决了柱坐标系的奇点影响剪切稀化流体分层Poiseuille流动数值求解的问题。东北石油大学崔海清带领的科研团队[11，12]首次利用待定系数法变换幂律流体在管内做行星运动的环空流方程，建立了给定流量情况下幂律流体在内管做行星运动的环空流压力梯度和内管壁所受流体作用力的数学模型，导出了内管壁上的法向应力差、切向应力和扭矩的计算公式，并利用有限差分法对其数值计算。

21世纪初国外专家克服边界服役条件复杂和非牛顿流体非连续性的难点，寻求数值算法解决其数模难题。2003年，Filip P.和David J.[13]分析了同心环空中符合R-S模型的非牛顿流体轴向层流，用几何、动力和流变参数获得的半解析准则多元化表示段塞流区相关位置的所有可能情况。2012年，Wilson H.J.[14]提出非牛顿流体的非连续性和不稳定性特征虽已得到很好的实验验证，至今却难以完全用数值模拟和解析法来描述。近年来，挪威专家Gjerstad K.带领科研小组[15，16]建立了H-B非牛顿流体圆管层流近似模型，其摩擦压力梯度满足显性连续可微，可用于控制、实时优化和预测钻井操作，与其他隐性算法比较精度高。

10余年来，从非牛顿流体油管流动数学物理模型的建立和初边值条件的确定，到解的存在性和唯一性证明及模型求解，都有深入研究。非牛顿流体的非连续性和不稳定性特征，亟需结合实际工况实验结果开展数模仿真来进一步揭示，得到半经验半解析式来进一步预测这些特征。笔者曾从非牛顿油管流动的物理现象出发，采用不需判断原油流变性质的赫巴流模式本构方程，确定其屈服值、稠度系数和流变指数。结合细管式流变仪测得的原油流量与压降数据，回归得到该原油的赫巴模式半解析式，实现原油的精细、经济输送[17]。采用分层雷诺数建立非牛顿流体赫巴流在管流和环空流的流态稳定性计算模型，找到非牛顿流油管流动过渡流区的最易失稳位置，得到了可供现场钻井液合理使用的流态判据[18]。

2非牛顿流体油井管流动

油气勘探开发过程中，涉及到了大量的非牛顿流体环空管流，诸如钻井液携岩携水循环机理、抽油杆泵和螺杆钻具的往复运动及工具润滑剂选用等。流道空间的几何非对称性，导致了非牛顿环空管流流态及流动规律的复杂性。

2.1环空分层流

非牛顿流体偏心环空层流中，极值流速所在坐标位置偏向内管，而且随环空间隙的增大而越偏向内管，宽间隙处的极值流速大于窄间隙处的极值流速。影响宽边极值流速与窄边极值流速比值的主要因素是偏心度ε和流性指数n，偏心度ε越大、流体非牛顿性越强，宽窄边的极值流速相差也越大。同种流体在不同环行空间中流动时，内外径之比越小，速度分布偏离几何中心越远。一般情况下，内外径之比大于0.8时，可认为流动对称于环行空间的几何中心柱面而不会引起太大的误差。

2.2环空过渡流

在偏心环空轴向流动中，环空断面上不同位置的流质发生失稳的临界水力条件，反映了该点的流动强度与紊动条件。流质在环空中处于局部紊流时，断面上分布有层流、过渡流及紊流三种状态。国外学者主要研究了水平井钻柱偏心环空旋进时非牛顿流体钻井液的局部紊流特征。2006年，Kim Y.J.等[19]模拟了钻柱旋转的直径比为0.52的同心环空非牛顿流体过渡流特征，发现过渡流可以揭示雷诺数与罗斯比数同表面摩擦系数的关系，进而理解过渡流不稳定机理。国内学者主要研究了稠油开采时非牛顿流体环空油流的局部紊流特征。2007年，李阳等[20]对稠油井抽油杆环空流模型的研究结果表明，环空偏心度是引起流场分布不均匀的主要参数，调整环空几何结构或流体流变性均可获得设计的局部紊流流场。

2.3环空紊流

工程中普遍存在的环空紊流现象国内研究较少，较深入的工作也仅为紊流压降的量纲和实验分析[21]，无法揭示流场分布的规律和特性。在全断面充分紊流条件下，剪切应力主要由雷诺应力τ′构成，利用普朗特动量交换理论，环空不同切向处的紊动强度可由边界层厚度及摩阻流速给予描述[22]。以非牛顿流体流变学理论和人工举升理论为基础，按照不同环空流动规律，李阳等[20]给出稠油井从地层到井口垂直井筒流动的运动方程和边界条件并求解，得到稠油井幂律流流动视粘度模型，为稠油井非牛顿流体流动优化设计提供理论参考。2010年，贾泽琪和韩洪升[23]将数值模拟和PIV技术结合用于非牛顿流体在偏心环空非定常流动研究，为掌握聚驱井产出液在抽油杆轴向往复运动的井筒中的流动规律提供有价值的理论参考。

国外研究环空紊流现象主要涉及水平井钻柱偏心环空旋进时非牛顿流体钻井液的携岩携液能力和螺旋流特征。2004年，Savins J.G.和Wallick G.C.[24]提出定量预测剪切粘滞性流体在螺旋流场中轴向泵排、压力梯度、角速度和扭矩耦合作用下的流动规律，其中最有趣的结果是耦合作用下的轴向流动阻力小于螺旋流的，即在指定轴向压力梯度下，螺旋流的轴向泵排比纯环空流场的要高。2010年，Ozbayoglu E.M.和Sorgun M.[25]对钻柱旋转的偏心水平环空中非牛顿流体摩擦压力损耗修正因子进行精确研究，通过大量不同非牛顿钻井液在不同钻柱转速下的试验数据，发现钻柱转速对环空压耗的影响是独立的。

3非牛顿流体输送管流动

3.1圆管分层流

圆管分层流是圆管两相流的一种基本流型，是下倾管中出现的主要流型，也是其他流型产生的基础。2000年，郑永刚等[26]提出圆管分层流新模型，利用该模型研究了非牛顿流体在圆管中层流-紊流分层流动，得出其速度场分布的解析式，进而研究了分层流的阻力规律，为分层掺气减阻提供了理论依据。在输送流性指数n较大的高粘幂律流体时，适当添加天然气或水等粘度较小的牛顿流体，形成幂律-牛顿流体圆管稳定的分层层流，比单一输送高粘幂律流体高效节能。添加适当的低粘牛顿流体可增加高粘幂律流流量最高达40%，而且添加的牛顿流体粘度越小，则比单一输送高粘幂律流体的节能效率越高。2003年，贺成才[27]通过精确地数值计算确定一个最佳的低粘牛顿流体的添加量，比单一输送流性指数n较大的高粘幂律流体增加流量达15.2%～38.25%。然而，在输送流性指数n较小的高粘幂律流体时，无论添加什么样的低粘流体都不可能实现高粘幂律流体的流量增加。

国外学者在非牛顿流体圆管分层流方面的理论研究远超国内水平，21世纪以来挪威学者在此领域研究尤为突出。2007年，Holmås K.和Biberg D.[28，29]发现通过水力相似转换得到的Biberg分层流管流等效直径与良好的压力梯度的CFD仿真结果较好吻合，表明明渠流对圆管流的转换是有效的建模工具，为大型管道系统的油气分层流模拟精度提供了潜力。2013年，Lawrence C.等[30]建立了凝析气和轻质油的油气水多相流新力学模型，修正了因管径和流体性质的比例放大行为，降低了与流体性质和管线尺寸相关的显著影响试验数据合理性的不确定性。凝析气重点研究了三维预集成三相分层流模型，改进湍流闭包和液滴与气泡传输的分散模型，作为预测凝析气管线中液体积聚发生的基础。

如何实现高含蜡高凝高粘原油圆管分层流的高效流动，已成为减小输送能耗提高效益的关键，研究人员大都通过使用添加剂或改变输送条件以破坏原油自身分子结构改变其物理属性，来达到对原油除蜡降凝降粘，从而影响圆管分层流流型流态的转变。挪威学者对圆管三维多相分层流相间交互作用机理的研究，或为进一步提高非牛顿流体管输效率搭建平台。

3.2非定常流

上世纪国内学者对非牛顿流体圆管非定常流动的研究[31，32]可知，非牛顿粘弹性流体在管内的不定常流动，弹性效应对其流动稳定性的影响，取决于流动类型和模型的选择。从扰动中获取弹性能时，流动更稳定，反之更不稳定。研究时有必要区分两种不同的流动：在材料和空间意义上都是定常的流动；只在空间意义上定常，而在材料意义上非定常的流动。前者可只限于注意现在时刻扰动是在增长还是在衰减，后者需考察材料元的变形历史、提取或释放弹性能的能力。这种能力取决于它的储能能力和已储能的大小。

近年，国内外在此方面的研究成果很少。2008年，王廖沙等[33]给定突扩管前后管直径比观察分歧流动现象，研究了恒剪切速率下不可压缩非牛顿流体在突扩管中的流动行为。2010年，崔海清科研团队[11,12,34]建立了变系数二阶流体在内管做轴向往复运动的偏心环空中非定常流的瞬时压力梯度方程和时均压力梯度公式，并给出相应的数值计算方法。2011年，Gainville M.和Sinquin A.[35]在第7届天然气国际会议上公布了输送管层流与紊流的水合物段塞流特征。

非牛顿非定常流动规律常成混沌状态，很多流动参数理论解的存在性和唯一性尚待证明，需要借鉴国外有限成果进一步对非牛顿流体微观结构和流变特性的相互关系与数学模型的建立上深下功夫，海洋管非牛顿水合物段塞流便是其中一个方向。

4非牛顿流体管流流态判别

自雷诺1883年提出临界雷诺数判别层流与紊流临界状态以来，据层流稳定性现象提出的判别流态转变的准则主要有：雷诺提出的雷诺数Re、瑞安和约翰逊提出的稳定性参数Z、汉克斯提出稳定性参数Ha、Mishra和Tripthi提出的稳定性参数X、岳湘安以涡流模型为基础提出的稳定性参数Y等。牛顿流体的临界雷诺数有明确的临界值，而非牛顿流体的临界雷诺数均为其流变参数的函数。事实上，只有牛顿流体与幂律流体圆管流的临界雷诺数值有实验依据，而其环空管流的临界雷诺数则属于外推。

目前，非牛顿流体管流流态稳定性判别理论按其基本模型可分为局部稳定性理论和整体稳定性理论。局部稳定性理论可从微观上精确分析非牛顿流体管流中紊动初始点，整体稳定性理论则从宏观上表征流体稳定性。从整体稳定性理论出发，在前人成果基础上[28,36-39]，归纳出幂律流体和宾汉流体分别在圆管和环空中的流态判别M-T稳定性参数X表达式(1)～(4)，涡流模型稳定性参数Y表达式(5)～(8)，以及幂律流体流态判别平均视粘度雷诺数Reu表达式(9)～(10)。M-T稳定性参数X一般用来分析判断实验时流体的流态，涡流模型稳定性参数Y考虑了涡旋流体宏观性质上的随机性与脉动，平均视粘度雷诺数Reu则考虑了断面流速变化对宏观流态的影响。关于局部稳定性参数Z的表达式可参见文献[18]详述。针对某种流动条件下的圆管非牛顿流体流动，可以先通过试验测定其相应的稳定性参数临界值，然后依据上述幂律或宾汉流体的流态判别式，外推判别不同流变性、过流几何尺寸和初边值下相应非牛顿流体的流态。

4.1M-T稳定性参数X

1)幂律流体稳定性参数X

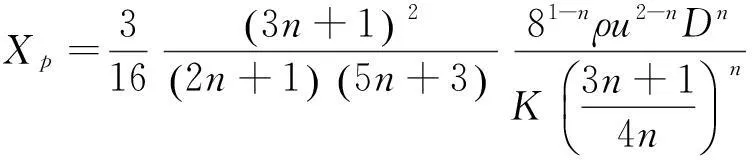
(1)

式中，n为流性指数；K为稠度系数；ρ为液体密度；u为速度分布；D为圆管内径；下标p为圆管。

环空中

(2)

式中，Da为环空管外径；da为环空管内径；下标a为同心环空。

2) 宾汉流体稳定性参数X

圆管中

(3)

式中，η为塑性流体的塑性粘度；α为核隙比；yp为与流速垂直方向的坐标。

环空中

(4)

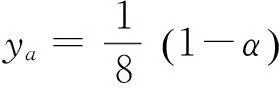
4.2涡流模型稳定性参数Y

1) 幂律流体稳定性参数Y

圆管中

(5)

式中，um为截面平均流速。

环空中

(6)

2)宾汉流体稳定性参数Y

圆管中

(7)

环空中

(8)

4.3幂律流体平均视粘度雷诺数Reu

圆管中

(9)

式中，下标u为平均。

环空中

(10)

从圆管和环空幂律流体稳定性参数式可知，幂律流稳定性与流变指数、稠度系数、密度、流速和过流断面当量直径有关。同种非牛顿流体流动，在相同流速下其稳定性是一致的；但流速不同时，会引起流变指数和稠度系数的差异，导致其稳定性也有显著差异，这也是非牛顿流体难以统一进行流态区域划分的原因。在相同条件下，容易证明判别非牛顿流体流态的岳湘安涡流稳定参数Y比M-T稳定性参数要大，说明考虑涡流扰动时非牛顿流体更容易成为混沌紊流。宾汉流体受启动压力环空宽窄间隙比的影响，会在环空流宽窄间隙处的稳定性差异会较大。从整体稳定性和工程应用来说，也用幂律流体视黏度雷诺数对非牛顿流体流态进行粗略判别。不过，由于非牛顿流体流动的流变性差异，在研究流态变化机理时还需结合上述3种流态判别法，在试验和实践比对基础上具体情况具体分析。

5非牛顿流体流动实验

非牛顿流体流变测量，一般是在一定条件下，对流体施加切应力，跟踪其受力响应而得，具有非单项性、非单值性和非可逆性的特点。2006年，张金亮等[40]研究了辽河油田超稠油的流变特性，通过试验确定该超稠油的流体类型，找出超稠油牛顿流与非牛顿流的转变点，归纳出其流变方程；王志华[41]通过室内建立的小型管流结蜡环道实验装置，研究了大庆肇源油田高凝原油在输油管道中的蜡沉积速度，考察了蜡沉积规律受温度的影响，并利用差热扫描量热仪从微观角度分析测试了蜡沉积物特性，探讨了结蜡机理和影响管壁结蜡的因素。2007年，张劲军等[42]用旋转粘度计对原油在温度扫描条件下粘温关系进行实验研究，建立了特征温度与剪切过程粘性流动熵产的经验关系式。2010年，贾泽琪和韩洪升[23]开展了对幂律流体在内管做轴向往复运动的偏心环空非定常流的数值模拟，建立了一套可调偏心度、冲程和冲次的垂直环空管道装置对其模拟结果进行PIV测试验证。

21世纪计算机技术与数值分析等学科的发展，计算机编程和数值模拟软件计算非牛顿流体流动问题成为热点，在工程允许误差范围内使用，解决了大量工程实际问题，成为了非牛顿流体实验手段的重要补充，从而推动了非牛顿流体的数值理论发展和工程应用。

6几点建议

1) 非牛顿流体偏心环空轴向流中，内外径之比大于0.8时，可假设流动对称于环形空间的几何中心柱面而不会引起太大误差。偏心度ε是引起流场分布不均匀的主要参数，可调整环空几何结构或流体流变性获得设计流场。目前，对几何轴对称的非牛顿流体非线性流动，还可以用弹性数和无量纲相似数描述其流动状况，难点在于像内外径之比小于0.8的偏心环空非牛顿流体流动机理就很难描述，需要运用混沌理论结合数模仿真技术进行评估。

2) 非牛顿流体圆管分层流混输技术中，可结合高分子纳米材料特性和电磁场理论，研制一种智能流体。纳米材料混入非牛顿流体中改变其流变性和磁性，电磁场可控制含纳米材料的流动屈服，这种智能流体可实现增大流性指数n较小的高粘幂律流体在分层流时的流量，以实现原油的低温输送。

3) 非牛顿流体圆管非定常流中，国外在粘弹性流体纯弹性不稳定现象方面做了大量深入研究，国内在借鉴其成果的基础上，可从高等流体力学、弹塑性力学、时均流、能量扰动及混沌学等基础理论出发，逐步建立非牛顿流体在空间意义上定常、材料意义上非定常流动稳定性的基础理论，探索非牛顿流体非定常流动规律。

4) 非牛顿流体管流稳定性研究中，非牛顿流体流动对附加扰动非常敏感，非牛顿流体流动的复杂性导致了难以准确描述其流态变化，还需通过大量可视化试验来深入研究其流型流态变化机理。

参 考 文 献

[1] 张劲军，严大凡.幂律流体在圆管内湍流流动剪切率的近似计算[J].水动力学研究与进展，2003，18(2)：248-252.

[2] Yin G L,Dong B Q.Asymptotic behavior of solution to equations modelling non-Newtonian flows [J].J.Math.Res.Exposition,2006,26(4): 699-706.

[3] 张其亮，张兴伟，宋娟，等.三维非牛顿流体动力学方程衰减性的一个注记[J].高校应用数学学报A辑，2010，25(1): 122-126.

[4] 谭启建，冷忠建.一类退缩非线性自由边值问题弱解的存在唯一性[J].数学杂志，2006，26(6): 657-664.

[5] 赵辉.有界区域上p(x)-Laplacian问题解的存在性[D].哈尔滨：哈尔滨工业大学，2006.

[6] 赵永杰.一个非自治不可压缩非牛顿流体在局部一致空间中的研究[D].兰州：兰州大学，2008.

[7] 郭春晓.随机非牛顿流解的适定性及其动力系统的研究[D].绵阳：中国工程物理研究院，2010.

[8] 朱克勤，杨迪，胡开鑫.粘弹性流体的分数元模型及圆管起动流[J].力学季刊，2007，28(4)：521-527.

[9] Liu Y Q,Zhu K Q.Axial Couette-Poiseuille flow of Bingham fluids through concentric annuli [J].J.Non-Newtonian Fluid Mech.,2010,165(21-22): 1494-1504.

[10] 孙学卫.剪切稀化流体分层流动的线性稳定性研究和数值模拟[D].北京：清华大学，2011.

[11] 修德艳.幂律流体在内管做行星运动的环空中流动的压力梯度[D].大庆：大庆石油学院，2007.

[12] 裴晓含.幂律流体在内管做行星运动的环空中流动时内管壁的受力分析[D].大庆：大庆石油学院，2007.

[13] Filip P,David J.Axial Couette-Poiseuille flow of Power-Law viscoplastic fluids in concentric annuli [J].J.Pet.Sci.Eng.,2003,40(3-4): 111-119.

[14] Wilson H J.Open mathematical problems regarding non-Newtonian fluids [J].Nonlinearity,2012,25(3): 45-51.

[15] Gjerstad K,Time R W,Bjørkevoll K S.Simplified explicit flow equations for Bingham plastics in Couette-Poiseuille flow-for dynamic surge and swab modeling [J].J.Non-Newtonian Fluid Mech.,2012,175-176: 55-63.

[16] Gjerstad K,Ydstie B E,Time R W,et al.An explicit and continuously differentiable flow equation for Non-Newtonian fluids in pipes [J].SPE J.165930,2013,19(1): 78-87.

[17] 李孝军，练章华，赖天华，等.赫-巴模式在原油管流测量中的应用[J].油气田地面工程，2008，27(5)：18-19，21.

[18] 李孝军，练章华，陈小榆，等.赫-巴流体稳定性参数Z的解析解分析[J].西安石油大学学报(自然科学版)，2010，25(1)：57-60.

[19] Kim Y J,Yoon C H,Park Y C,et al.Vortex flow study on Non-Newtonian fluids in concentric annulus with inner cylinder rotating [C].Proc.16thInt.Offshore Polar Eng.Conf.,San Francisco,California,USA,2006: 835-839.

[20] 李阳，张凯，王亚洲，等.稠油油井幂律流体流动视黏度模型[J].石油勘探与开发，2007，34(5)：616-621.

[21] 岳湘安，陈家琅，刘宏，等.泥浆模拟液在偏心环形空间中的紊流[J].大庆石油学院学报，1991，15(1): 33-39.

[22] 王艳辉.偏心环空非牛顿流体紊动场特性的研究[J].水动力学研究与进展，1997，12(2): 150-156.

[23] 贾泽琪.偏心环空中非定常流场数值模拟及PIV实验研究[D].大庆：大庆石油学院，2010.

[24] Savins J.G.,Wallick G.C.Viscosity profiles,discharge rates,pressures,and torques for a rheologically complex fluid in a helical flow [J].AIChE J.,2004,12(2): 357-363.

[25] Ozbayoglu E.M.,Sorgun M.Frictional pressure loss estimation of Non-Newtonian fluids in realistic annulus with pipe rotation [J].J.Canadian Pet.Technol.,2010,49(12): 57-64.

[26] 郑永刚，谢翠丽，姚泽西.非牛顿流体在圆管中层流-紊流分层流动规律[J].四川大学学报(工程科学版)，2000，32(3)：1-4.

[27] 贺成才.幂律-牛顿流体圆管分层层流的数值模拟[J].天然气与石油，2003，21(1): 18-21.

[28] Biberg D..An engineering model for two-phase stratified turbulent duct flow [J].Multiphase Sci.and Tech.,2004.

[29] Holmås K.,Biberg D..Comparison of the Biberg analytical depth-integrated two-phase stratified flow model with CFD simulations [C].13thInt.Conf.on Multiphase Prod.Technol.,Cannes,France,BHR Group June 2007: 121-137.

[30] Lawrence C.,Nossen J.,Skartlien R.,et al.Mechanistic models for three-phase stratified and slug flows with dispersions [C].16thInt.Conf.on Multiphase Prod.Technol.,Cannes,France,BHR Group June 2013: 283-296.

[31] 刘慈群，黄军旗.非牛顿流体管内不定常流的解析解[J].应用数学和力学，1989，10(11): 939-946.

[32] 陈文芳，范椿.非牛顿流体流动的不稳定性[J].力学进展，1985，15(1): 49-53.

[33] Wang L S,Jiang J F,Hong R Y,et al.Transition to asymmetry of Non-Newtonian fluids: in an abrupt expansion [J].Comput.Appl.Chem.,2008,25(12): 1473-1476.

[34] 李楠.粘弹性流体在内管做轴向往复运动的偏心环空中非定常流的压力梯度[D].大庆：大庆石油学院，2010.

[35] Gainville M,Sinquin A.Hydrate slurry characterization for laminar and turbulent flows in pipelines [C].Proc.of the 7thInt.Conf.on Gas Hydrates,Edinburgh,Scotland,United Kingdom,17-21 July,2011.

[36] 李兆敏，蔡国琰.非牛顿流体力学[M].东营：石油大学出版社，2001.

[37] 刘乃震，王廷瑞，刘孝良，等.非牛顿流体的稳定性及其流态判别[J].天然气工业，2003，23(1): 53-57.

[38] 何世明，罗德明，虞海生，等.判别液体流态的层流稳定性理论[J].天然气工业，2000，20(5): 67-69.

[39] 刘崇建，刘孝良，柳世杰.非牛顿流体流态判别方法的研究[J].天然气工业，2001，21(4): 49-52.

[40] 张金亮，王为民，申龙涉，等.辽河油田超稠油流变特性的试验研究[J].油气田地面工程，2006，25(7): 11.

[41] 王志华.高凝原油管道输送蜡沉积规律实验研究[J].特种油气藏，2006，13(5)：91-93.

[42] 张劲军，朱英如，李鸿英，等.含蜡原油特征温度实验研究[J].石油学报，2007，28(4)：112-114.

[43] Ahmed R,Miska S.Experimental study and modeling of yield Power-Law fluid flow in annuli with drillpipe rotation [C].SPE Drill.Conf.112604,2008.

[44] Japper-Jaafar A.,Escudier M.P.,Poole R.J..Laminar,transitional and turbulent annular flow of drag-reducing polymer solutions [J].J.Non-Newtonian Fluid Mech.,2010,165: 1357-1372.

[45] Erge O,Ozbayoglu E M,Miska S Z,et al.The effects of drillstring eccentricity,rotation and buckling configurations on annular frictional pressure losses while circulating yield Power Law fluids [C].SPE Drill.Conf.167950,2014.

Study Advances and Suggestions on Non-Newtonian Fluid in Oil Tubular Flow

LI Xiaojun,LIU Yonggang,LIN Kai,LIU Wenhong

(CNPC Tubular Goods Research Institute,State Key Laboratoryof Performance and Structural Safety for Petroleum Tubular Goods and Equipment Materials,Xi’an,Shaanxi 710077,China)

Abstract：The research progress of non-Newtonian-fluid oil tubular flow in recent 10 years was summarized in 5 aspects，including mathematical models and computing methods,stratified and unsteady flow in circular pipe,flow law of annular pipe flow,flow regime discrimination,and flow tests of non-Newtonian fluid.The base of researches on non-Newtonian-fluid flow and rheological behaviors is to establish the constitutive equation and determine the rheological parameters of non-Newtonian fluid flow,which plays an important role in developing theory of non-Newtonian fluid mechanics and solving problems of production technology.Based on predecessors’ returns,according to research advances in non-Newtonian-fluid oil tubular flow,it is proposed to combine polymer material science,electromagnetic,elastic-plastic theory,thaology,and modern computer finite element numerical simulation with higher fluid mechanics to seek thoughts to solve problems in terms of stratified-flow mixing transport technology,stability and flow law of unsteady flow,turbulent flow law in annuli in non-Newtonian fluid pipe flow and correlativity and rationality of flow regime criterion,etc..

Key words：non-Newtonian fluid;mathematical model;pipe flow;annular flow;flow regime;simulation tests

基金项目：中国石油天然气集团公司应用基础研究项目“复杂工况气井油套管柱失效控制与完整性技术研究”(编号：2014A-4214)

第一作者简介：李孝军，男，1982年生，工学博士(后)，2012年博士毕业于西南石油大学油气井工程专业，现在中国石油集团石油管工程技术研究院从事油井管与管柱工程技术方面的研究。E-mail：lixiaojun003@cnpc.com.cn。

中图法分类号：TE8

文献标识码：A

文章编号：2096-0077(2016)03-0008-07

(收稿日期：2015-09-04编辑：屈忆欣)