关于Fibonacci与Lucas数的求和

刘小宁

(武汉软件工程职业学院　湖北　武汉：430205)



关于Fibonacci与Lucas数的求和

刘小宁

(武汉软件工程职业学院湖北武汉：430205)

摘要提出并证明了Fibonacci数与Lucas数的一个求和公式。

关键词Fibonacci数；Lucas数；求和；公式

Fibonacci数与Lucas数在组合数学、信息论和植物学等领域应用广泛[1-6]。基于文献[7]，文中提出并证明Fibonacci数与Lucas数的一个求和公式。

当n为正整数，Fibonacci数Fn与Lucas数Ln的直接计算公式为[1]：

(1)

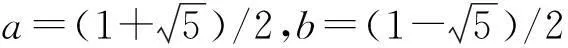
定理1对于正整数m、n、λ与非负整数r，有：

定理2对于正整数m、n、λ与非负整数r，有：

定理1的证明 根据等比数列求和公式与式(1)可得：

(2)

注意到ab=-1，将式(2)整理可得到定理1，证毕。

同理可证定理2。

当正整数m、n与λ取不同值时，根据定理1、2和式(1)，可得到许多恒等式。

参考文献

[1]陈景润.组合数学简介[M].天津:天津科技出版社,1988:94-105.

[2]王婷婷.Fibonacci数列倒数的无穷和[J].数学学报,2012,55(2):517-524.

[3]赵艳.广义Fibonacci-Lucas数中的素数问题[J].浙江大学学报(理学版),2005,32(1):10-12,16.

[4]张强,任小永,陈乾宏,等.基于Fibonacci数列的MPPT仿真与初步实验[J].电工电能新技术,2013,32(2):28-33.

[5]邹建成,石志鑫.一种基于Fibonacci数系的数字水印新方法[J].电子学报,2011,39(7):1598-1602.

[6]胡宏.植物叶序中的Fibonacci数和Lucas数的反演[J].安徽农业科学,2009,37(19):8812-8813.

[7]刘小宁.Fibonacci与Lucas数的一个求和公式[J].武汉工程职业技术学院学报,2014,26(3):94, 98.

(责任编辑：李文英)

Summation of Fibonacci and Lucas Numbers

Liu Xiaoning

(Wuhan Vocational College of Software and Engineering, Wuhan 430205, Hubei)

Abstract:A summation formula of the Fibonacci-Lucas numbers is put forward and proved.

Key words:Fibonacci numbers; Lucas numbers; summation; formula

收稿日期：2016-05-23

作者简介：刘小宁(1963～)，男，教授，正高职高级工程师，硕士生导师.E-mail：lxngjxy@163.com

中图分类号：O156.1

文献标识码：A

文章编号：1671-3524(2016)02-0076-01