上海经济综合影响力的定量评估研究*
2016-07-21宣子岳朱家明张素洁张庆茹
宣子岳,朱家明,张素洁,张庆茹
(1.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030;2.安徽财经大学 金融学院,安徽 蚌埠 233030)
上海经济综合影响力的定量评估研究*
宣子岳1,朱家明1,张素洁1,张庆茹2
(1.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030;2.安徽财经大学 金融学院,安徽 蚌埠 233030)
摘要:针对近十年上海市在长三角经济圈的作用和影响的评估,选取上海在长三角经济圈内经济综合影响力排名以及上海市在空间范围内的辐射力大小及带动作用两个方面来研究,使用因子分析、线性拟合等方法,分别构建主成分-因子、相关性分析等模型,得到上海的经济综合影响力在长三角排名第一,上海对苏州、杭州、嘉兴等地的影响和带动作用较大等结论.
关键词:上海市经济综合影响力;主成分分析;聚类分析
长江三角洲城市群是我国城市化程度最高、城镇分布最密集、经济发展水平最高的地区.长三角经济圈是以上海为中心,南京、杭州为副中心,包括江苏的苏州、无锡、徐州、扬州、泰州、南通、镇江、常州、盐城、淮安、连云港、宿迁,浙江的宁波、温州、嘉兴、湖州、绍兴、舟山、台州、金华、衢州、丽水,安徽的合肥、马鞍山,芜湖、滁州、淮南共30个城市.以沪杭、沪宁高速公路以及多条铁路为纽带,形成一个有机的整体.
目前,我国正处于经济发展的转型期,因此寻找新的经济增长点至关重要.如何利用中心城市拉动周边区域的经济增长,增强中心城市的经济辐射力度,研究和解决这一问题对促进我国下一步经济增长具有深远的意义.
1数据来源与模型假设
(1)数据来源.数据来源于上海市统计年鉴、江苏省统计年鉴和浙江省统计年鉴,时间跨度为2005-2014年,选择了GDP等指标对问题进行分析.
(2)模型假设.①假设官方给出的统计数据信息真实可靠;②假设选取的长三角地区的13个城市的经济不受外围经济圈的影响;③假设经济只受选取的8个指标的影响;④忽略南京作为江苏省省会对周边城市的经济影响.
2长三角地区各个城市的影响力评估模型
为了对长三角地区各个城市的影响力进行排名,首先搜集到长三角地区13个主要城市的地区生产总值GDP、第二产业增加值、第三产业增加值、人均GDP、工业增加值、各项存款总额、固定资产投资总额、社会消费品零售总额这8大指标2013年的数据,建立主成分-因子模型,筛选出两个重要的主成分进行分析,最后得出长三角13个主要城市的经济影响力排名.
2.1模型建立
对于成本型指标,无量纲化处理为
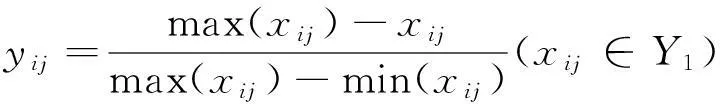
对于效益型指标,无量纲化处理为
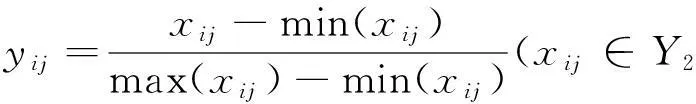
无量纲化后的决策矩阵为Y=(yij)m×n,显然指标经过极差变换后,均有0≤yij≤1,且各指标下最好结果的属性值是yij=1,最坏结果的属性值是yij=0.指标变换前后的属性值成比例.
(2)相关性分析.相关性分析即应用相关系数公式,计算出两个变量之间相关系数的值,分析变量之间的相互关系.相关系数记为r,公式如下:
相关系数r的绝对值,恒小于或等于1.若|r|≥0.8表明两变量之间高度相关;0.5≤|r|<0.8表明两变量之间中度相关;0.3≤|r|<0.5表明两变量之间低度相关;|r|<0.3表明两变量之间关系极弱,认为不相关.
(3)主成分分析.设对某一事物的研究涉及i个指标,分别用x1,x2,…,xi表示,这i个指标构成的随机向量为X=(x1,x2,…,xi).对X进行线性变换,可得k个新的综合变量,用y表示,即
根据方差最大化原理,主成分问题实质是变量间的方差最大化,Var(yi)=Var(aix')=aiCai,ai=(ai1,ai2,…,aim),C为协方差矩阵.
基于上述原则和条件决定的综合变量y1,y2,…,分别称为原始变量的第一,第二,…,第n个主成分.其中,各综合变量在总方差中占的比重依次递减,在实际研究中为了简化系统结构抓住实质,通常只挑选前几个方差最大的主成分.
2.2结果分析
根据上述因子得分矩阵,得到相应的因子得分函数为
y1=0.16x1+0.133x2+0.17x3-0.011x4+
0.13x5+0.182x6+0.099x7+0.168x8,
y2=-0.113x1+0.102x2-0.233x3+0.843x4+
0.125x5-0.378x6+0.294x7-0.202x8.
计算出因子1和因子2的权重分别为0.685和0.315,因此得到用于计算城市综合排名的函数为y=0.685y1+0.315y2,根据此函数可以得到长三角地区13个城市的综合得分排名,如表1所示.
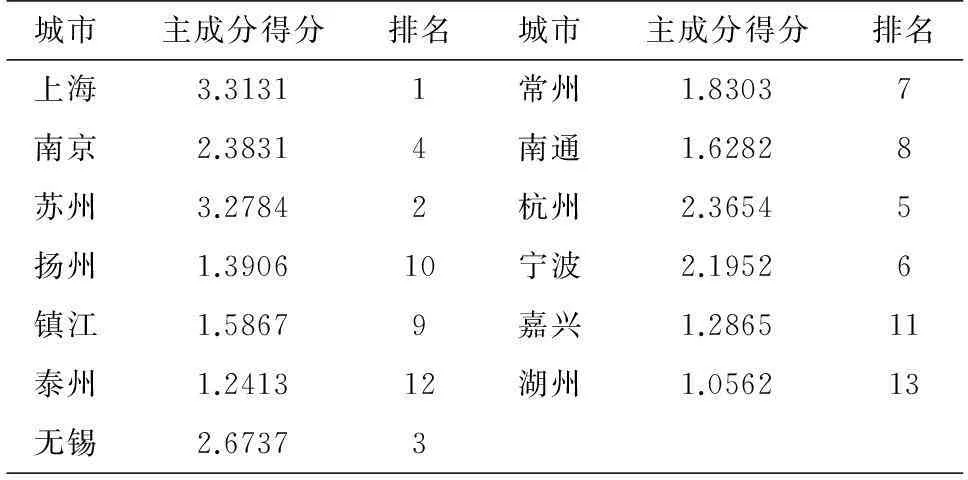
表1 长三角地区的13个城市的综合得分排名
由表1可知,长三角地区各城市综合经济实力评价结果为(从高到低排序):上海、苏州、无锡、南京、杭州、宁波、常州、南通、镇江、扬州、嘉兴、泰州、湖州.因此可得出结论,长三角地区经济实力最强的城市是上海市,其次是苏州市,经济实力最弱的城市是湖州市.
3以GDP为指标的定量评估模型
为了定量评估上海近十年在长三角城市的经济影响力,以GDP为指标,采用线性拟合的方法,建立相关分析模型,定量计算上海GDP每增长一个百分点,其余城市的GDP增长量,继而将上海在长三角地区的经济影响力进一步量化,增加模型的可信度.
3.1模型建立
(1)城市GDP的相关性.GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标.中心城市的经济辐射力对周边城市在科技、就业、投资、产业迁移等各个方面的影响最终都会不同程度上体现在一个城市的GDP中.因此,首先选择GDP作为一项重要的分析指标.假定在特定的城市经济圈内,中心城市的经济辐射力将发挥巨大作用,以至于其GDP的增长将不同程度上拉动或减缓周边城市GDP的增长.可以对两部分数据进行回归,并对回归结果进行检验,从而验证假设的合理性.将排名前四的城市2005-2014年间的GDP水平通过柱状图反映出来,如图1所示.

图1 2005-2014年长三角主要城市的GDP(单位:亿元人民币)
从图1看出,维持经济圈内中心城市GDP增长的各种要素,势必经由形形色色的经济效应转移作用于周边经济圈城市.中心城市的经济辐射力越强,其GDP的增值将带动周边城市GDP更大幅度的增长,反之亦然.
(2)相关分析.相关分析即应用相关系数模型,计算出两个变量之间相关系数的值,分析变量之间的相互关系.相关系数记为r,设有两对变量x和y,其相关系数r的模型计算公式为
相关系数r的绝对值,恒小于或等于1.若|r|≥0.8表明两变量之间高度相关;0.5≤|r|<0.8表明两变量之间中度相关;0.3≤|r|<0.5表明两变量之间低度相关;|r|<0.3表明两变量之间关系极弱,认为不相关.
通过建立相关分析模型,运用SPSS软件计算上海与周边主要城市的GDP指数的相关关系得到拟合曲线和相关系数,从而得出上海对长三角经济圈其他城市的作用和影响力大小.
3.2结果分析
为了消除各城市GDP总量上的差别,以2005年为基准,将上述各城市的GDP除以2005年数值得出GDP指数,并利用SPSS绘制散点图,如图2所示.由图2可知,苏州的GDP指数与上海GDP指数大致呈线性关系.对指数进行回归处理.回归结果表明,上海GDP与苏州GDP相关比例很高,相关系数达0.9925.利用MATLAB软件进行显著性检验,数据通过了参数显著性检验.
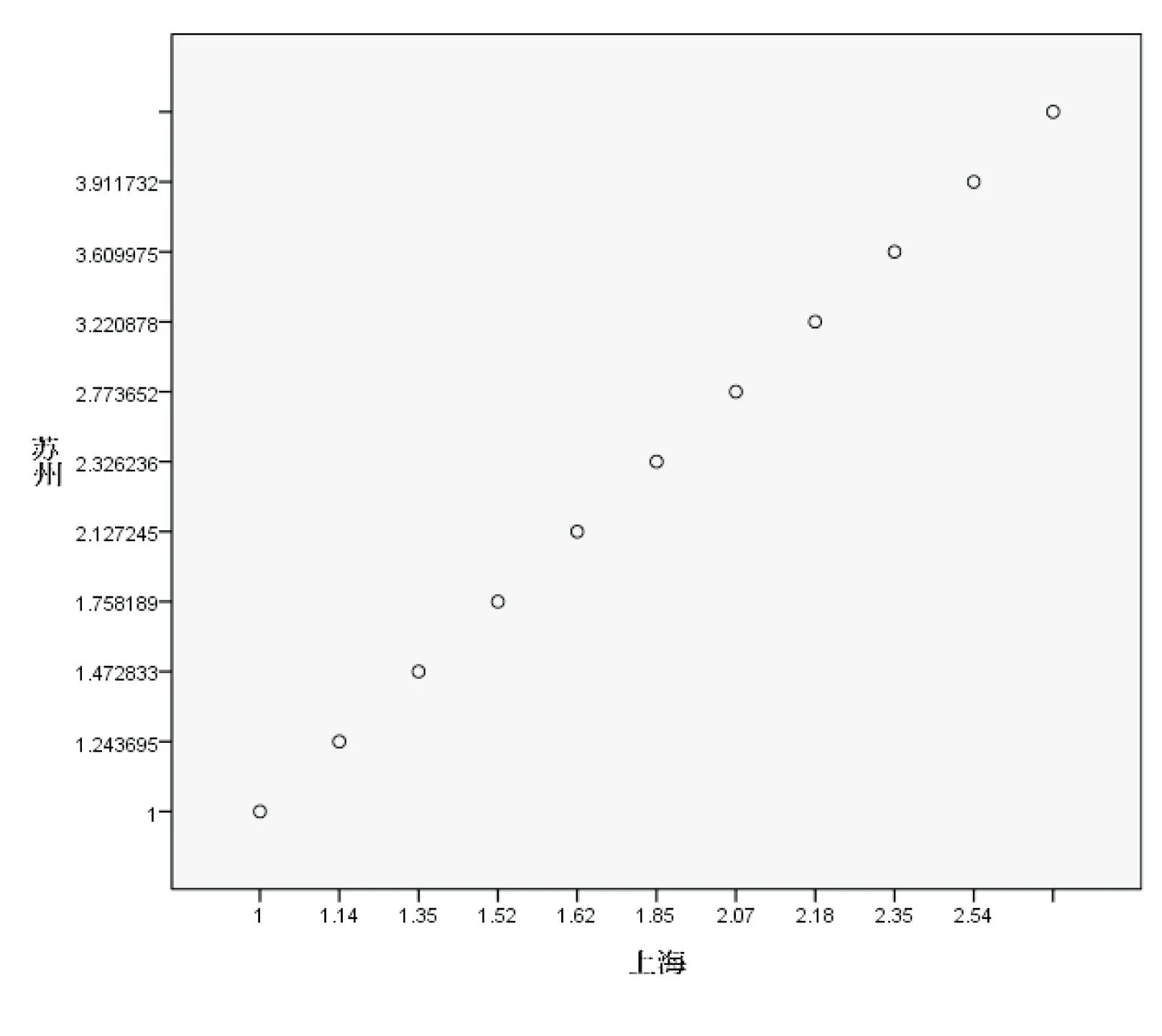
图2 上海-苏州GDP相关分析的散点图
苏州与上海的GDP指数间的关系为gsz=1.9148gsh-1.0379,亦即上海GDP每增长1个百分点,将带动苏州GDP增长1.9148个百分点.上海与周边主要城市GDP指数的相关关系,如表2所示.

表2 各城市与上海GDP的相关系数
4结束语
目前在长三角地区,上海市的整体经济实力最强,而且远高于周边其他城市.在长三角经济圈内,上海市对其周边城市的经济辐射强度存在较大差异.
(1)嘉兴、湖州、宁波、杭州等作为距离上海最近的地区,受上海的影响最强,存在明显的“同城效应”;
(2)扬州、泰州、镇江距离上海稍远,主要受到省会南京的辐射影响;
(3)南通是江苏省内距离上海第二近的城市,仅次于苏州.但南通与上海间有长江相隔,历史上交通一直不方便.因而其受上海影响较小.宁波距上海虽然较远,但宁波凭借深水港优势,成为上海重要的出海口、贸易中转站,以及能源、原材料基地,因此其与上海的联系非常紧密;
(4)南京作为江苏省的省会,本身就是一个极具影响力的大城市,其GDP增长更多由自身因素决定,又因为距上海最远,所以其受上海经济辐射强度最低.
参考文献:
[1]宇传华.SPSS与统计分析[M].北京:电子工业出版社,2007.
[2]陆炳炎.长江经济带发展战略研究[M].上海:华东师范大学出版社,l999.
[3]杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科技大学出版社,2013.
[4]谷人旭,殷为华.论长江三角洲都市经济圈的形成及其核心城市上海的功能定位[J].地域研究与开发,2001,20(1):27-30.
[5]解瀛.上海世博会对长三角地区经济影响评估[J].安徽理工大学学报,2011,13(4):20-23.
(责任编辑:陈衍峰)
DOI:10.13877/j.cnki.cn22-1284.2016.06.016
*收稿日期:2015-12-04
基金项目:国家自然科学基金项目“随机动力系统的非一致指数二分性及其数值模拟”(11301001);安徽财经大学科研项目“数学建模竞赛引领大学生科研创新的研究”(acjyzd201429)
作者简介:宣子岳,女,安徽滁州人,安徽财经大学统计与应用数学学院在读.
通讯作者:朱家明,安徽泗县人,副教授.
中图分类号:O29
文献标志码:A
文章编号:1008-7974(2016)03-0045-03
