基于WCPF和FRFT的LPI信号识别研究*

赵凯凯，杨承志，王龙

(空军航空大学 信息对抗系，吉林 长春　130022)



基于WCPF和FRFT的LPI信号识别研究*

赵凯凯，杨承志，王龙

(空军航空大学 信息对抗系，吉林 长春130022)

摘要：针对低截获概率雷达信号难以识别和分类的问题，提出了基于加权型三次相位函数(weighted-type cubic phase function, WCPF)和分数阶傅里叶变换(fractional fourier transform, FRFT)的低截获概率雷达信号识别算法。用短时傅里叶变换剖析了应用较广的8种低截获概率雷达信号的时频特性，然后依据调频率将其分为2类。先用加权型三次相位函数估计信号的调频率，然后再用分数阶傅里叶变换获得信号的各分量峰值，根据峰值能量比进行细分类。通过大量的实验仿真验证，在信噪比为0 dB的条件下，正确识别率能够达到95%以上。

关键词：三次相位函数；分数阶傅里叶变换；低截获概率；峰值能量比；信号识别；调频率

0引言

电子侦察系统包括雷达侦察和通信侦察系统，担负着战场态势感知和引导干扰的任务，是平台与武器的“耳目”与“大脑”，更是电子战行动的前提和保障。然而，为提高战场反侦察能力，大量的低截获体制雷达与通信设备被集成到作战飞机、面对空地防空系统中，使电子侦察装备普遍出现“失灵”与“失效”。伴随低截获概率(lowprobabilityofintercept，LPI)雷达在战场上涌现的是大量的低截获信号，它们往往经过复杂调制，使雷达告警器无法侦察告警，飞行员感知不到威胁对象，导致作战平台被“静悄悄击落”。因此，复杂调制LPI信号的识别研究已是当前紧迫的军事需求。

目前，很多文献对雷达信号的识别进行了研究，现有的雷达脉内识别方法主要有信号瞬时时域特征法[1]，调制域分析法[2]，高阶矩累计量法[3]，时频分析法[4]，谱相关分析法[5]等。

此文着重研究低截获概率雷达信号的分类识别问题。先利用短时傅里叶变换(STFT)剖析了8种常见的LPI信号的时频特性。然后根据时频特征，利用加权型三次相位函数(WCPF)对LPI信号进行初步分类。最后再利用分数阶傅里叶变换(FRFT)对初分类后的信号进行细分类。通过仿真验证，该方法可以在较低的信噪比条件下获得较高的识别率，对实际工程有一定的参考价值。

1LPI信号的时频特性分析

目前，低截获概率雷达采用的信号大体分为3类，调频信号、相移键控信号和频移键控信号[6]。其中运用最广泛的调频信号是线性调频连续波信号(LFMCW)；相移键控信号包括巴克多相序列和弗兰克(Frank)码，以及P1～P4码和多时编码T1～T4码[6]；频移键控信号应用比较广泛的是Costas跳频信号。

下面列出8种常用LPI信号时频图，如图1所示。由LPI雷达信号时频图可以将它们分为两大类，第1类信号是调频率为0的BPSK和Costas信号；第2类信号是调频率不为0的LFM，Frank码，P1～P4码信号，其中P2码信号调频率为负，Frank，P1，P3和P4码信号调频率为正，易知LFM信号调频率可正可负。同时印证了文献[6]的理论：多相压缩编码源于近似步进调频波形(Frank，P1，P2码)和线性调频波形(P3，P4码)。从时频分布的角度来看，多相编码信号等价于具有同一调频率的多分量LFM信号[7]。

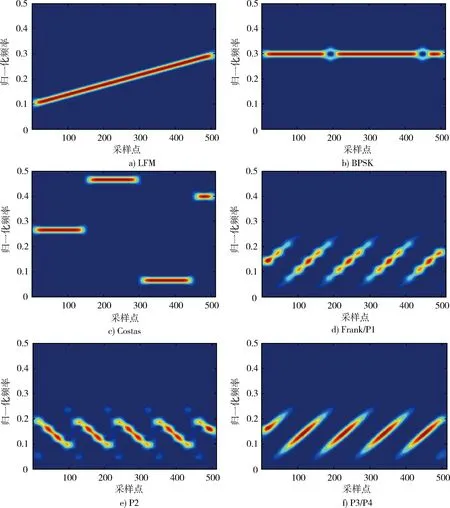
图1　低截获概率雷达常用信号时频图Fig.1　Eight common LPI signals time-frequency image

2加权型三次相位函数(WCPF)算法及仿真

2.1算法原理

文献[8]中，O＇SheaP提出了三次相位函数法[9]，对信号进行二阶变换，通过该变换的最大值就可以估计信号的调频率[10]。三次相位函数在估计调频信号时具有高精度和良好低信噪比能力[11]，如式(1)：

(1)

式中：k代表瞬时频率率(IFR)[12]，在本文中也可理解为调频率，其定义式如式(2)所示。

IFR(t)=d2φ(t)/dt2.

(2)

线性调频信号s(t) = Aexp[j2π(at+bt2)]的三次相位函数为

(3)

式中：η(t)=exp[j2π2(at+bt2)].

由式(3)可以得出，三次相位函数在调频斜率处形成峰值。离散情况下，设信号的采样点数为N，则信号的三次相位函数的表达式如式(4)所示。

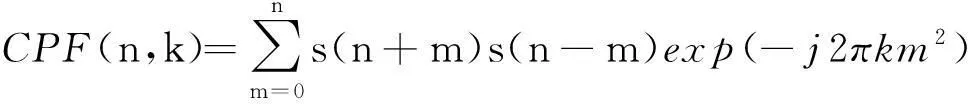
(4)

式中：n遍历取采样点数N内的所有数值;k依然表示调频率。

本文对三次相位函数进行演变，把各自调频率下的三次相位函数所有采样点求和再取平均，把二维的三次相位函数转换成更加直观的一维调频率k的函数，其表达式如式(5)所示。然后通过一维函数的峰值来确定信号调频率的估计值，为信号调制类型的初步识别提供依据。

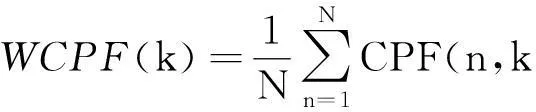
(5)

2.2算法仿真

由LPI时频特征分析获知：BPSK，COSTAS信号调频率为零，Frank，P1，P3，P4信号调频率为正，P2信号调频率为负，LFM信号调频率可正可负。下面通过加权型三次相位函数图，验证分析结论是否正确。

通过图2容易得到：调频斜率为0的是BPSK和Costas信号，进一步细分BPSK信号和Costas信号的方法将在下节阐述；调频率为正的是Frank，P1，P3，P4码，调频率为负的是P2信号，虽然图2a)显示LFM的调频率为正，但是从线性调频信号的表达式可知LFM信号的调频率也可能为负，下节将进一步区分多相码信号和LFM信号。本节在区分第1类信号和第2类信号时，通过大量仿真，设定误差因子δ=0.03。

3LPI信号分数阶傅里叶变换及仿真

3.1分数阶傅里叶变换(FRFT)

傅里叶变换是一种线性算子，若将其看作从时间轴逆时针旋转π/2到频率轴，则分数阶傅里叶变换就是可旋转任意角度α的算子，并因此得到信号新的表示[12]。分数阶傅里叶变换保留了传统傅里叶变换原有性质和特点的基础上又添加了其特有的新优势，可认为分数阶傅里叶变换是一种广义的傅里叶变换[13]。

分数阶傅里叶变换是一种统一的时频变换，随着阶数从0连续增长到1，分数阶傅里叶变换展示出信号从时域逐步变化到频域的所有变化特征，可以为信号的时频分析提供更大的选择余地[13]。p=0时，分数阶傅里叶变换就是原函数，p=1时是傅里叶变换[13]。定义在t域的函数x(t)的p阶FRFT如式(6)所示。

(6)

图2　常用LPI信号的WCPF图Fig.2　Common LPI signals WCPF image

(7)

3.2第1类LPI信号细分类算法原理及仿真

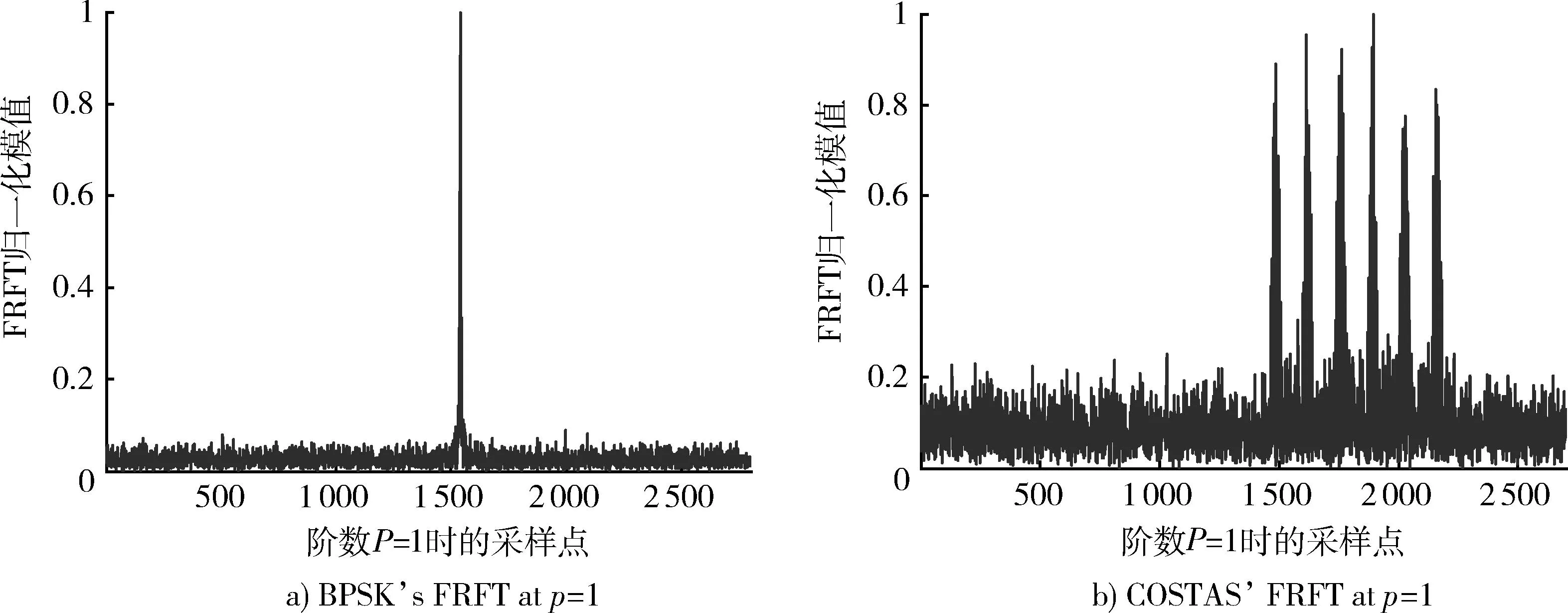
图3　第1类LPI信号分类仿真Fig.3　Simulation of the first kind of LPI signals

3.3第2类LPI信号细分类算法原理及仿真

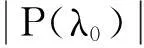
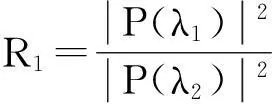
(8)

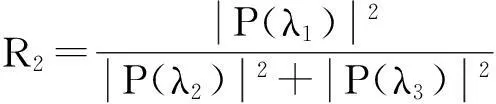
(9)

经过大量仿真实验得出，峰值相对能量关系随着采样率的改变很小，因此峰值能量比可以作为识别多相码的理论依据。表1是经过大量仿真得到的关于峰值能量比的数据。

表1　多相码信号峰值能量比

图4只是给出了多相码信号各分量之间的相对关系，由于低截获概率雷达采用了功率管理技术，其发射的LPI信号的信噪比会比较低，而FRFT只能把多相码信号较强的分量体现出来，能量比R1要比R2更可靠，因此本文将依据能量比R1对多相码信号进行分类，R2可以用来辅助识别。通过大量实验发现，在信号的信噪比低于-6dB时，峰值能量比无规律可循，因此本文算法只适用于接收信号不低于-6dB的情况。下面通过设定能量比R1的阈值区间来识别多相码信号(SNR≥-6dB)，具体规则如式(10)所示。

(10)

4LPI信号识别分类方法流程及性能分析

总结以上对LPI信号识别分类算法的研究，下面给出识别流程图如图5所示。

下面通过MonteCarlo仿真实验，对本文算法进行性能分析。本文算法分类对象是8种低截获概率雷达信号。信号具体参数：BPSK信号按照7位巴克码编码，载频是5MBZ；LFM信号调频带宽为2MBZ，载频为5MBZ；COSTAS跳频信号频率序列为{3 2 6 4 5 1}MBZ；多相码信号载频为5MBZ。所有试验的采样频率都设为20MBZ，采样点数为512点，信噪比范围是-6～6dB。每2dB进行400次MonteCarlo仿真，最后得到本算法识别性能曲线如图6所示。

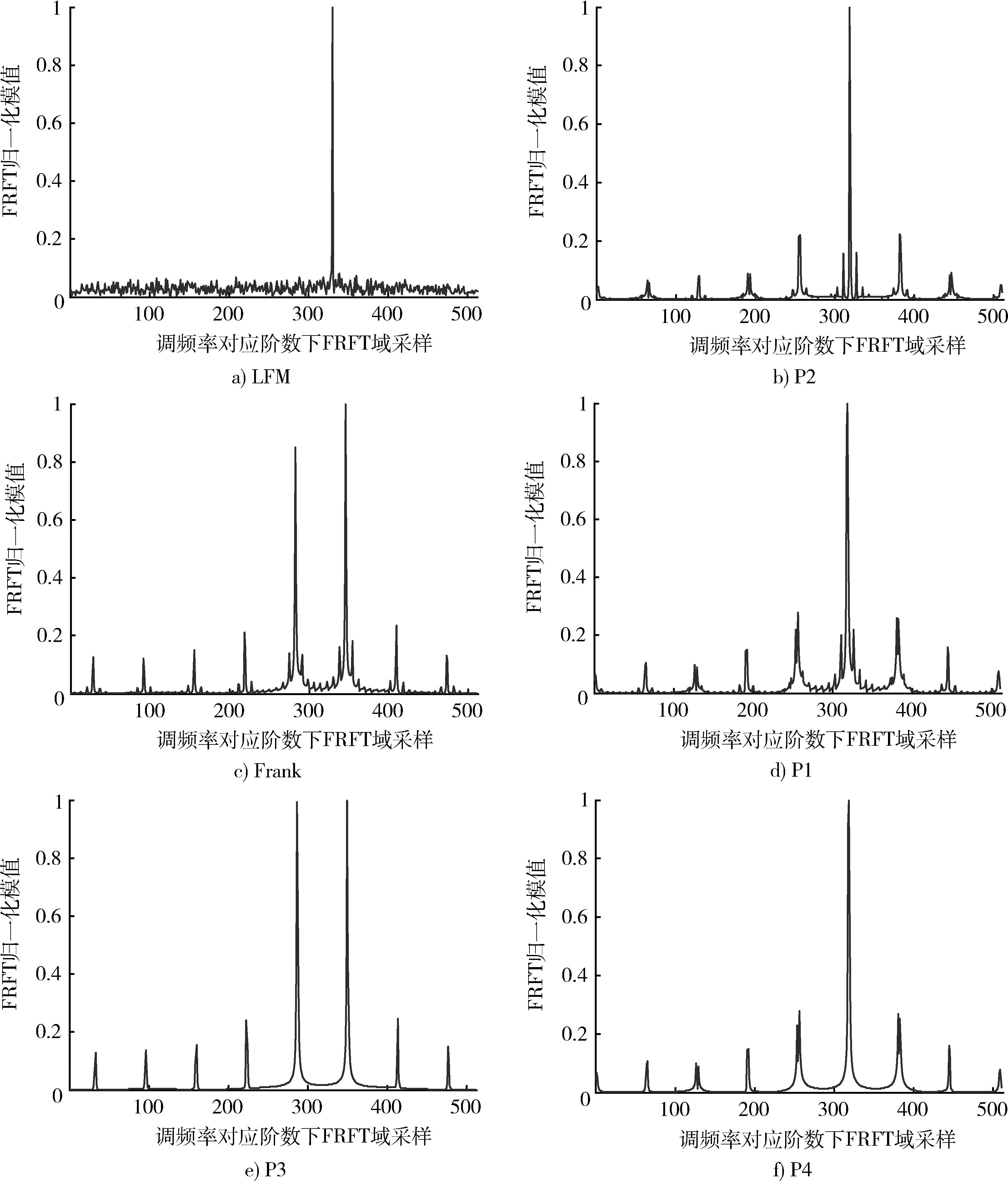
图4　LFM信号和多相码信号在调频率对应阶数FRFT域采样Fig.4　LFM and Poly-phase signals FRFT sampling at corresponding order

图5　LPI信号分类识别流程图Fig.5　LPI signals classification and recognition diagram

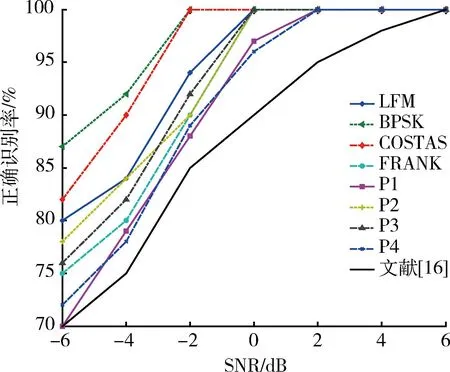
图6　本文算法识别性能图Fig.6　Identification performance of this thesis

由图6的仿真结果可以看出，本文算法的正确识别率要优于文献[16]。文献[16]采用频域滤波然后瞬时相位拟合算法在信噪比不低于0dB时，正确识别率在90%以上，而本文算法在信噪比为0dB时，前面分析的8种LPI信号的正确识别率都超过95%，除P1，P4码信号以外，其余6种LPI信号的正确识别率都达到100%。而BPSK信号和COSTAS信号的识别率在信噪比为-2dB时已经达到了100%，因为WCPF的抗噪性能非常好[10]，即使在很低的信噪比下也能很好地估计出信号调频率，同时COSTAS信号各个频率成分的能量近似相同，FRFT可以把它们体现出来。由于分数阶傅里叶变换只能把多相码信号较强分量体现出来，而由图4可以看出在单周期时，Frank和P3码有2个主分量，P1和P4码只有单个主分量，次强峰值易受噪声影响，强噪声会湮没次强峰值，P1码和P4码信号易被误识别为LFM信号，所以P1码和P4码信号的识别率相对要差一些。

5结束语

本文在分析8种常用低截获概率雷达信号的时频分布的基础上，通过加权型三次相位函数获得信号的调频率，对截获的信号进行初分类。然后再利用初分类中的调频率估计分数阶傅里叶变换的阶数，并在相应阶数下进行FRFT域采样，最后依据峰值相对关系对初分类后的信号细分类。经过大量仿真，本文算法在信噪比为0dB的条件下，8种常用LPI信号的正确识别率都达到了95%以上。

参考文献：

[1]ZAKIMJ.EfficientlyMiningFrequentTreesinaForest[C]∥Proceedingsofthe8thACMSIGKDDInternationalConferenceonKnowledgeDiscoveryandDataMining.NewYork:ACMPress, 2002:71-80.

[2]NANDIAK,AZZOUZEE．AlgorithmsforAutomaticModulationRecognitionofCommunicationSignals[J].IEEETransactionsonCommunication,1998,46(4)：431-436．

[3]CHAOJIV,HASANMA,SALEMS,etal.AnIntegrated,GenericApproachtoPatternMining:DataMiningTempleLibrary[J].DataMiningandKnowledgeDiscovery, 2008,17(3):457-495.

[4]韩国成．雷达信号脉内调制特征的时频分析[J]．航天电子对抗，2004(3)：34-37.

HANGuo-cheng.Time-FrequencyAnalysisforIntra-pulseModulationCharacteristicsofRadarSignal[J].AerospaceElectronicWarfare, 2004(3): 34-37.

[5]GARDNERAW,SPOOERCW.CyclicSpectralAnalysisforSignalDetectionandModulationRecognition[J].MilitaryCommunicationConference, 1988, 38 (2)：419-424.

[6]PHILLIPEP.DetectingandClassifyingLowProbabilityofInterceptRadar[M].NewYork:ArtechHouse, 2009：83-103.

[7]徐会法，刘锋. 基于FRFT的一类低截获概率雷达信号调制识别[J]. 航天电子对抗，2011,27(2)：28-31.

XUHui-fa,LIUFeng.ModulationRecognitionofaKindofLowProbabilityofInterceptRadarSignalsBasedonFRFT[J].AerospaceElectronicWarfare, 2011,27 (2): 28-31.

[8]O＇SheaP.ANewTechniqueforEstimatingInstantaneousFrequencyRate[J].IEEETrans.onSignalProcessing, 2004, 52:385-393.

[9]杜清，王建.P3/P4 多相码雷达信号检测与参数估计研究[J]. 科学技术与工程，2013,13(19)：5673-5678.

DUQing,WANGJian.ResearchofDetectionandParameterEstimationforP3/P4PolyphaseCodesSignal[J].ScienceTechnologyandEngineering, 2013,13(19): 5673-5678.

[10]李利，司锡才，张雯雯，等. 改进的多分量LFM信号参数估计算法及快速实现[J].系统工程与电子技术，2009,31(11)：2560-2562.

LILi,SIXi-cai,ZHANGWen-wen,etal.ImprovedEstimationAlgorithmofMulti-ComponentLFMSignalParametersandItsFastImplementation[J].SystemsEngineeringandElectronics, 2009,31 (11):2560-2562.

[11]司伟建，蒋鹏，刘旭波. 改进的三次相位函数法LFM雷达信号参数估计[J]. 哈尔滨工程大学学报，2012,33(6):771-773.

SIWei-jian,JIANGPeng,LIUXu-bo.TheParameterEstimationofanLFMRadarSignalBasedonaModifiedCubicPhaseFunction[J].JournalofHarbinEngineeringUniversity, 2012,33(6):771-773.

[12]薛俊诗，张宝玲. 基于三次相位变换的多项式相位信号参数估计[J]. 国外电子测量技术，2013,32 (9):29-33.

XUEJun-shi,ZHANGBao-ling.ParametersEstimationforPolynomialSignalBasedonCubicPhaseTransform[J].ForeignElectronicMeasurementTechnology, 2013,32(9):29-33.

[13]陶然，邓兵，王越. 分数阶傅里叶变换及其应用[M]. 北京：清华大学出版社，2009：2-14.

TAORan,DENGBing,WANGYue.FractionalFourierTransformandItsApplications[M].Beijing:TsinghuaUniversityPress, 2009: 2-14.

[14]袁伟明，王敏，吴顺君. 低截获概率雷达信号的调制识别研究[J]. 信号处理，20062,2(2):153-156.

YUANWei-ming,WANGMin,WUShun-jun.StudyonModulationandRecognitionforLPIRadarSignals[J].SignalsProcessing, 2006,2(2):153-156.

[15]宁辉，陈超. 基于分数阶傅里叶变换的脉内信号调制方式识别[J]. 电讯技术，2011,51(12):42-47.

NINGHui,CHENChao.RecognitionofIntra-PulseSignalsModulationBasedonFractionalFourierTransform[J].TelecommunicationEngineering, 2011,51(12):42-47.

[16]赵锋，刘渝，杨健. 低信噪比下的脉内调制方式识别[J]. 数据采集与处理，2011,26 (5):615-618.

ZHAOFeng,LIUYu,YANGJian.Intra-PulseModulatedSignalRecognitioninLowSignal-to-NoiseRatio[J].JournalofDataAcquisition&Processing, 2011,26(5):615-618.

LPI Radar Signal Identification Based on WCPF and FRFT

ZHAO Kai-kai,YANG Cheng-zhi, WANG Long

(Aviation University of Air Force,Department of Information Countermeasures, Jilin Changchun 130022, China)

Abstract:Aiming at the problem that LPI radar signals are difficult to identify and classify, an algorithm of LPI radar signal recognition based on weighted-type cubic phase function and fractional Fourier transform (FRFT) is proposed. Eight common LPI radar signals are divided into two categories by frequency modulation (FM) rate after time-frequency characteristics analysis with short-time Fourier transform. Firstly, with an estimated FM rate of signals by weighted-type cubic phase function, peaks of each component are obtained by FRFT. Then, LPI signals are sub-classified according to the ratio of peak energy rate. Through a large number of simulation experiments, the correct identification rate can reach 95% with this algorithm under the condition of SNR=0 dB.

Key words:cubic phase function (CPF); fractional fourier transform (FRFT); low probability of intercept (LPI);peak energy ratio; signal recognition; frequency modulation(FM) ratio

*收稿日期：2015-05-06；修回日期：2015-07-15

作者简介：赵凯凯(1990-)，男，河南焦作人。硕士生，研究方向为低截获概率雷达信号识别与分类。

通信地址：130022吉林省长春市南湖大路2222号研究生队E-mail：kaikaiaizuqiu@126.com

doi:10.3969/j.issn.1009-086x.2016.03.029

中图分类号：TN911.6；TP301.6

文献标志码：A

文章编号：1009-086X(2016)-03-0186-08

军事电子信息系统